Ch3-6. Orthogonal Complement

Orthogonality는 선형차원 축소에 쓰인다. D차원의 vector space V와 M차원의 subspace U에 대해 orthogonal complemnet $U^⊥$은 D-M차원의 subspace이며, U의 모든 벡터에 직교하는 V의 모든 벡터를 포함한다. $U∩U^⊥={0}$이므로 V의 모든 벡터 x는 다음과 같이 분해되며 유일하다.

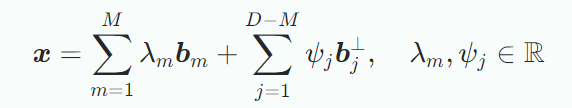
면 $U$에 직교하면서 $∥ω∥=1$인 벡터 $w$는 $U^⊥$의 기저벡터다. 아래 그림은 이를 보여준다. 그림에서 $w$에 직교하는 모든 벡터들은 $U$상에 놓여있으며 이때 $w$를 $U$의 normal vector라 부른다.