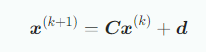Ch2-3.Solving Systems of Linear Equations

Particular and General Solution

다음의 세단계을 통하여 특수해와 일반해를 구할 수 있다.
1. $Ax=b$ 에서 특수해(particular solution)을 구한다.
2. $Ax=0$ 에서 모든 해를 구한다.
3. 1과 2를 통해 얻은 해를 결합하여 일반해(general solution)을 구한다.

특수해와 일반해를 구하기 쉽게 연립선형방정식을 간단한 형태로 변환하는 알고리즘을 가우스 소거법이라고 한다.

Elementary Transformations

elementary transformations을 수행해도 해는 변하지 않는다. 과정은 다음과 같다.
1. 두 방정식을 교환한다. (연립선형방정식을 표현하는 행렬의 행을 교환)
2. 0이 아닌 상수 $λ∈R$ 을 한 방정식에 곱한다.
3. 두 방정식을 더한다.

행의 선행 계수(왼쪽에서부터 0이 아닌 첫 번째 숫자)를 피벗이라고 하며, 각 행의 피벗은 위에 있는 행의 피벗의 오른쪽에 위치한다. 따라서, 모든 사다리꼴 형태의 연립방정식은 항상 계단 구조를 가진다.

사다리꼴 모양의 행렬은 다음과 같은 조건을 만족한다.

1. 0으로만 구성된 행이 행렬의 가장 아랫쪽에 위치한다. (0이 아닌 요소를 하나 이상 가지고 있는 행은 0으로만 구성된 행 위에 존재)
2. 0이 아닌 행만 봤을 때, 왼쪽에서부터 처음으로 0이 아닌 숫자(pivot or leading coefficient)가 항상 그 행의 윗 행의 피벗의 오른쪽에 위치한다.

사다리꼴 모양에서 피벗에 대응되는 변수들을 basic variables라고 하고, 나머지 변수들을 free variables라고 합니다.

사다리꼴 형태는 특수해를 쉽게 찾을 수 있게 해주는데 피벗이 존재하지 않는 열의 계수를 0으로 두고 특수해를 구할 수 있다.

아래의 조건을 만족하는 연립방정식을 reduced row-echelon form이라고 한다.
1. 사다리꼴 형태(row-echelon form)
2. 모든 피벗이 1
3. 피벗은 해당 열에서 0이 아닌 유일한 요소일 때

The Minus-1 Trick

$Ax = 0$ 해를 쉽게 구하는 트릭을 살펴보면 A가 reduce row-echelon form일 때, 피벗이 존재하지 않는 열에 -1이 피벗이 되도록 [0....-1....0] 형태의 n-k개의 행을 더하여 A를 n x n형태로 확장한다. 이때 피벗으로 -1을 가지는 열은 $Ax = 0$해가 된다. 즉, -1을 피벗으로 하는 열들은 $Ax = 0$의 solution space의 basis(기저)를 형성하며, 이를 kernel 또는 null space라고 부른다.

예시

위의 행렬에 피벗이 -1이 되도록 행을 추가하여 5 x 5 행렬로 변환

위 행렬로부터 대각 요소에 -1을 포함하는 열을 가지고, 바로 $Ax=0$ 의 해를 얻을 수 있다.

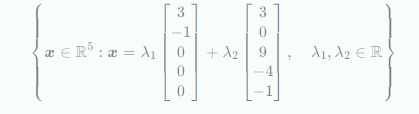
Algorithm for Solving a System of Linear Equations

$Ax = b$에서 A가 정사각 행렬이면서 역행렬이 존재할 때, 역행렬$A^{-1}$을 구할 수 있고
$x = A^{-1}b$로 해를 구할 수 있다. 위의 조건을 만족하지 않는다면 선형독립한 열들이 있다는 가정하에 아래의 변환을 사용할 수 있다.

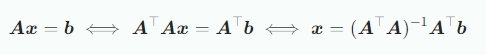
이러한 방법은 많은 연산이 필요하다는 단점이 있다.

가우스소거법은 행렬식(determinants)를 계산할 때, 벡터 집합이 선형 독립이라는 것을 확인할 때, 역행렬을 구할 때, 벡터 공간(vector space)의 기저(basis)를 결정할 때 중요한 역할을 한다.

가우스 소거법은 수백만개의 변수가 있는 경우에 필요한 연산이 너무 많아지기 때문에 반복법을 통해 간접적으로 해를 구한다. 반복법의 핵심은 모든 반복에서 해에 수렴하도록 적절한 C, d에 대해 아래와 같은 반복을 설정하는 것이다.