Ch2-4.Vector Spaces

Groups

집합 G과 연산 ⊗:G×G→G 가 G 에 대해 정의되어 있을 때, 아래의 조건을 만족하는 $G$:=(G,⊗)를 군이라고 부른다.

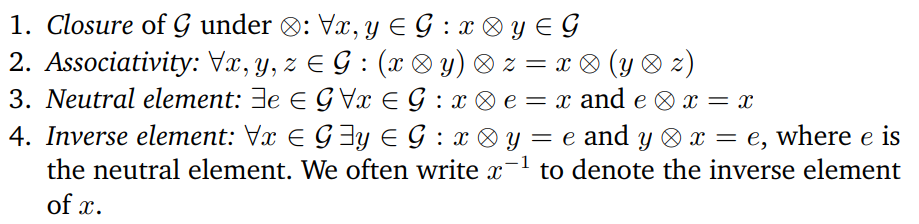
위의 조건에 추가로 $∀x,y∈G:x⊗y=y⊗x$(교환법칙)를 만족하면 해당 그룹을 아벨군이라고 한다.

역행렬이 존재하는 regular matrix A의 집합은 group이며, 이를 general linear group(일반 선형군)이라고 부르며 $GL(n,R)$ 로 표기합니다. 그러나, 행렬 곱은 교환법칙이 성립하지 않기 때문에 알벨군은 아니다.

Vector Spaces

위에서 군은 같은 집합내에서 정의되는 inner operation만 고려했다면 이번에는 벡터와 스칼라처럼 다른 집합간의 정의되는 outer operation도 포함되는 집합을 살펴본다.

실수인 벡터 공간 $V=(V,+,⋅)$ 은 아래 두 연산을 포함하는 집합 V이다.

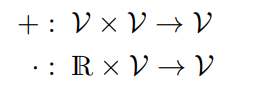
여기서 벡터공간은 다음과 같은 특성을 가지고 있다.

V에 속하는 요소들은 벡터라고 부른다. 벡터 공간에서 항등원은 0-벡터라고 하며,inner operation은 vector addition이라고 하며 outer operation ⋅ 은 multiplication by scalars이다.
벡터곱 $ab$는 정의되진 않는다 그냥 곱하면 벡터차원이 일치하지 않기 때문에 $ab^T$, $a^Tb$만 정의된다.

Vector Subspaces

$V$=(V,+,⋅) 가 vector space이고, U⊆V, U!=0 라고 할 때, $U$=(U,+,⋅) 을 $V$의 vector subspace라고 한다.U⊆V 이고 $V$ 가 vector spcae라면,
$U$는 $V$ 의 특성을 물려받는다. 여기에는 아벨군 속성, 분배 법칙, 결합 법칙, 항등원이 포함된다. $U$가 $V$의 부분공간인지 확인하려면 아래 조건을 확인하라.

모든 subspace $U⊆(R^n,+,⋅)$는 $x∈R ^n$인 $Ax = 0$의 해공간(solution space)이다.