Ch2-5.Linear Independence

아래의 형태를 만족하는 모든 v를 벡터 $x_1, ...., .x_k$의 선형결합이라고 한다.

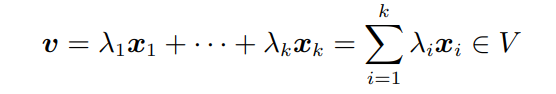
0벡터는 항상 선형결합을 표현이 가능하다. 여기서 우리는 계수가 전부 0이 아닌(자명하지않은) 선형결합을 찾는 것이 목적이다.

v = 0에서 계수가 하나라도 0이 아니라면 $x_1, ...., .x_k$를 선형종속이라 하고 계수가 전부 0일 때만 성립한다면 선형 독립이라고 한다.

가우스소거법을 통해 행렬을 변환한 후 모든 열이 피벗열이라면 모든 열 벡터들의 집합은 선형독립이며 피벗이 아닌 열이 존재한다면 선형종속이다.

벡터 공간 $V$ 에서, k 개의 벡터 $x_1, ...., .x_k$에서 m개의 선형결합의 벡터집합은 m >k일떄 선형종속한다.