Ch3-4. Angles and Orthogonality

Angles and Orthogonality

코시-슈바르츠 부등식을 사용하면 두 벡터 $x, y$가의 내적에서의 각도 $w$를 정의할 수 있다. x와 y가 0이 아닐 때, 다음과 같다.

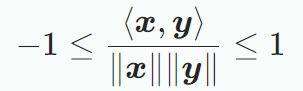
두 벡터간 유일한 각도 $w∈[0,π]$가 있을 때, 각도는 다음과 같다.

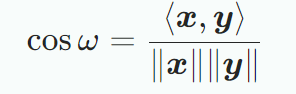
두 벡터 간의 각도는 두 벡터의 방향이 얼마나 유사한지 알려준다.
$⟨x,y⟩=0$가 0이라면, 두 벡터를 직교한다고 하고 $x⊥y$로 표현하며, 두 벡터의 norm이 1이라면 두 벡터를 orthonormal하다고 한다.

정사각행렬 $A∈R^{n×n}$가 orthonormal힐 때, $AA^⊤=I=A^⊤A$가 성립하면 A를 직교행렬이라고 하고 $A^{−1}=A^⊤$이 성립한다. 따라서 행렬을 전치하면 역행렬을 구할 수 있다.

직교행렬을 통한 변환은 벡터의 길이가 변하지 않는다.

또한, 두 벡터의 각도도 변하지 않는다.

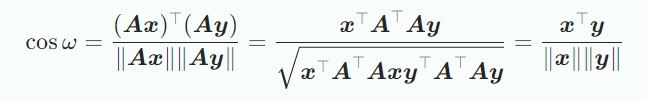
즉, 직교행렬은 angles와 distances를 보존한다.