Binomial - 이항분포

Binomial

이항분포는 확률변수 Random variable이 $n$번의 시행에 있어 1과 0 혹은 성공과 실패 등 2가지 값만 가지는 형태를 의미합니다.
즉 결과가 2가지 뿐이므로 이산확률분포에 속하며 만약 시행횟수가 1이라면 베르누이 분포와 동일합니다.
즉, 만약 $X_i \sim \textrm{Bernoulli}(p)$ 이라면
이항분포의 확률변수 $X$는 다음과 같습니다.

이항 분포는 시행횟수를 $n$, 성공확률을 $p$라고 가정했을 때 다음과 같이 표현합니다

Probabilty Function

pmf를 구하기 위해선 먼저 n번의 시행 중 성공 횟수(k)에 따른 확률을 구해야 합니다.
먼저 순서가 있는 n번의 시행 중 성공의 경우 k를 선택하는 경우의 수 값을 구해야 하므로 $\binom{n}{k} = \frac{n!}{k!(n-k)!}$로 표현됩니다.
그리고 해당하는 경우의 수에 해당하는 확률 값은 $p^{k} (1-p)^{n-k}$로 표현됩니다.

따라서 pmf는 다음과 같습니다.

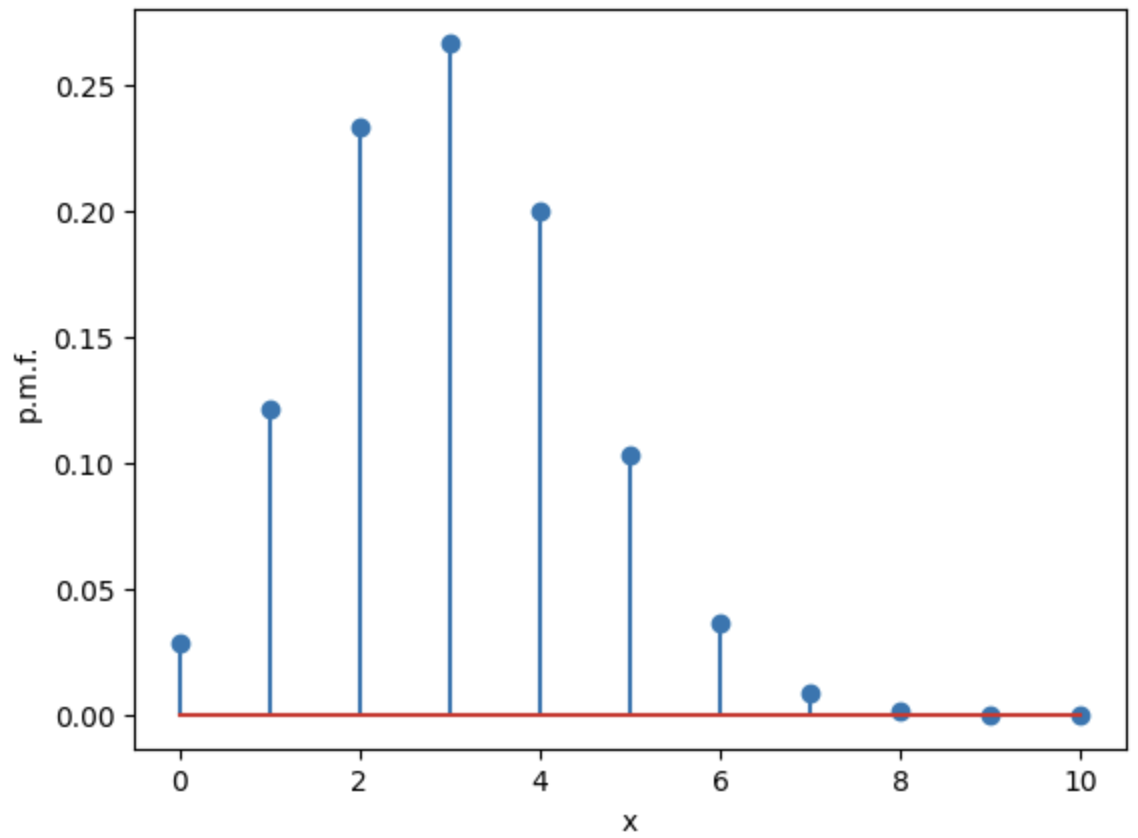
10번의 시행($n$)에 성공확률을 0.2($p$)라고 가정했을때 이항분포는 다음과 같이 생겼습니다.

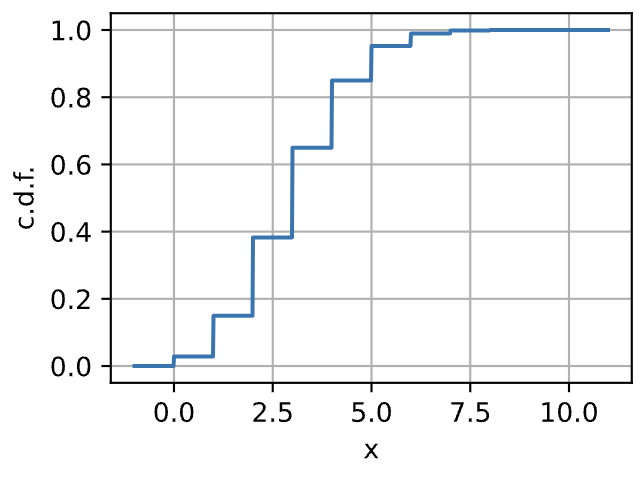
cmf의 수식과 함수는 다음과 같습니다.

Descriptive Statistics

References

[1][1] Zhang, A., Lipton, Z.C., Li, M. and Smola, A.J., 2021. Dive into deep learning. arXiv preprint arXiv:2106.11342.