Image Classification

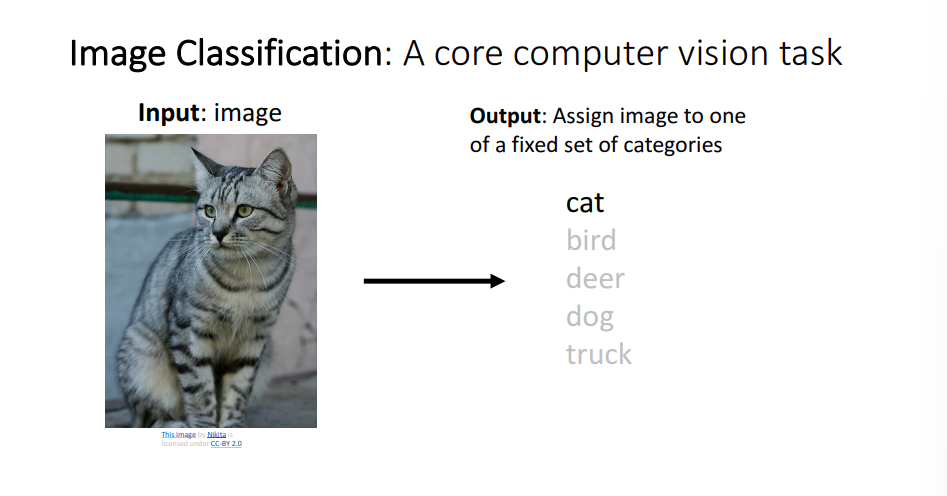
• Image Classification은 간단하지만 매우 중요.
• 사람은 직관적으로 고양이라고 구분할 수 있지만, 컴퓨터에겐 쉽지 않은 일이며 사람과 컴퓨터 사이의 차이 즉, Semantic Gap 문제가 발생.
  

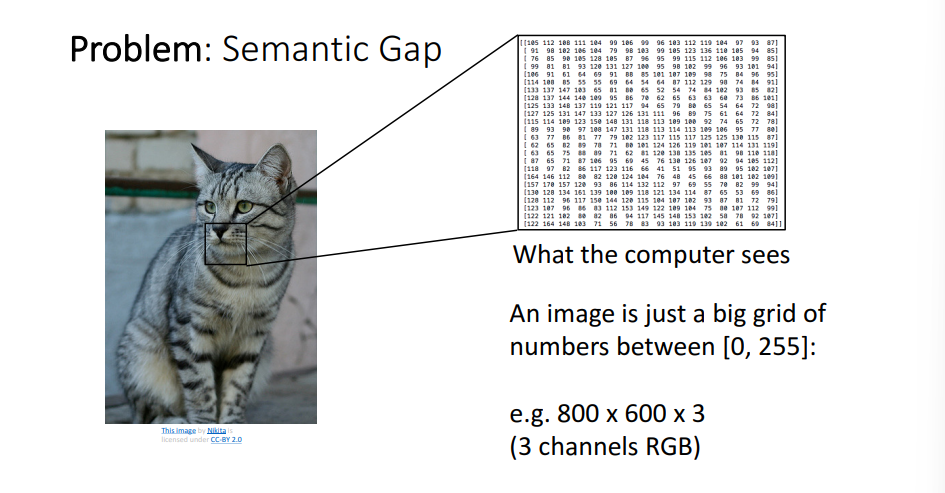
Challenges

• Viewpoint Variation
  
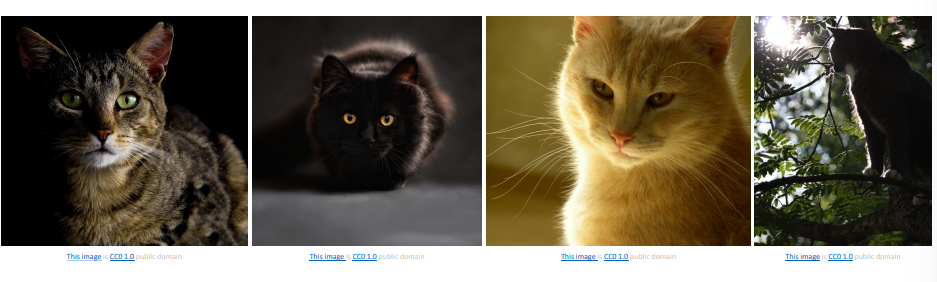
• Intraclass Variation
  
• Fine-Grained Categories
  
• Background Clutter
  
• Illumination Changes
  
• Deformation
  
• Occlusion
  
• 위의 어려움들을 해결하여 Image Classification은 의료, 천문학, 생물학 등 다양한 분야에서 유용하게 사용

Image Classification : Building Block for other tasks!

• Image Classification은 block 형식으로도 쓰이며, 이미지에 존재하는지 뿐만 아니라 어디에 존재하는지 까지 나타냄
  

• 이를 활용하여 그림에 맞는 문장을 생성
  

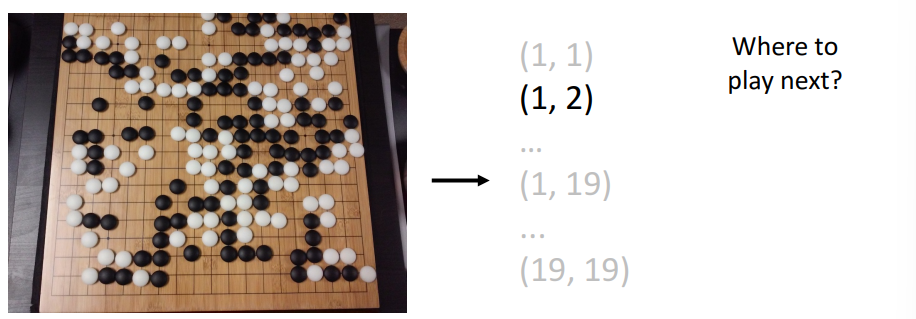
• 바둑에도 사용되어 다음수를 어디에 두어야 할지 결정

• 하지만 위의 문제들을 해결하고 적용하기에는 매우 어렵고 어떻게 해야할지 잘 모름

• 인간의 최대한의 지식을 사용하여 다른 객체들을 분류해주는 classifer에 정보를 전달해 주어야함.
  

• 이를 위해서 Edge 정보를 전달

• 그러나 이는 좋은 접근이 아니며 다루기 어려움

Machine Learning: Data-Driven Approach

• 대신 데이터 기반 머신러닝 시스템을 구축
• 먼저 데이터셋의 이미지들과 라벨들을 모으고
• 분류 모델을 학습하고
• 새로운 이미지를 추론
• 이 방식을 활용하면 두번 코드를 작성할 필요 없이 원하는 Object를 Detection하고 싶을때 특정Object의 이미지와 라벨정보를 모아서 학습 후 추론 가능

Image Classification Datsets

• MNIST
  

  • MNIST 데이터셋의 경우 컴퓨터비전의 초파리와 같다는데 이는 생물학에서 초기 실험에 초파리가 쓰이는것과 같이 가벼운 성능 확인을 위해서 MNIST 데이터셋이 쓰임을 의미

• CIFAR10
  

  • grayscale이 아닌 컬러가 들어가며 손글씨보다는 다양한 object에 더 관심

• CIFAR100
  

  • CIFAR10의 class 100 버전

• ImageNet
  

  • 논문이나 새로운 method를 제안할때 ImageNet의 결과가 없다면 거절당함 매우 중요하며 오늘날 Classification의 밴치마크로 사용됨

• MIT Places
  

  • ImageNet이 Object에 초점이 맞춰져 있었다면 MIT Places는 장소에 초점이 맞춰짐
    
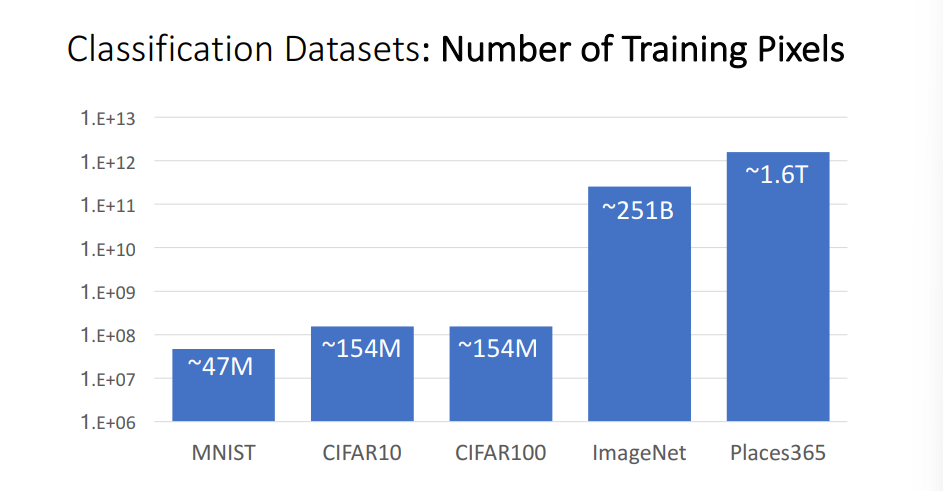
  • ImageNet의 경우 가장 크기가 크고 공신력이 있으며 간단한 학습의 경우 CIFAR을 사용하거나 MNIST를 사용

• Omniglot
  

  • 매우 여러개의 1623개의 카테고리가 존재하지만 각 카테고리에는 20개의 매우 적은 예를 통해서 학습시키고 추론
  • 이때 Low-shot Classification라 불리는 문제가 발생하며 이를 해결하기 위해서 사용되는 데이터

First classifier: Nearest Neighbor

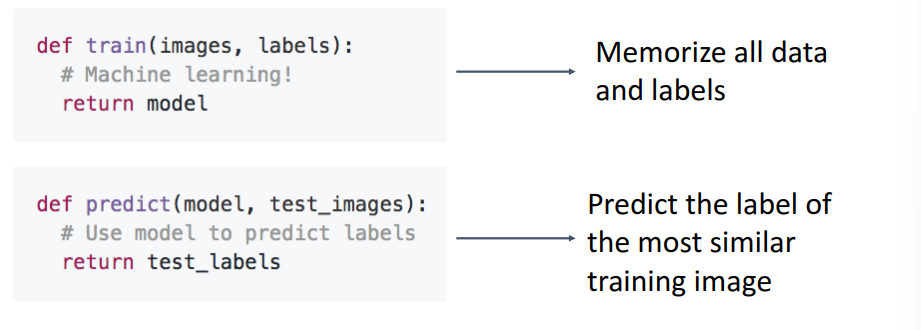
• 머신러닝을 구현할때 학습 함수와 추론함수 두가지 기능을 이용
• 학습 함수에는 이미지들의 유사도를 비교할 수 있는 알고리즘이 필요
  
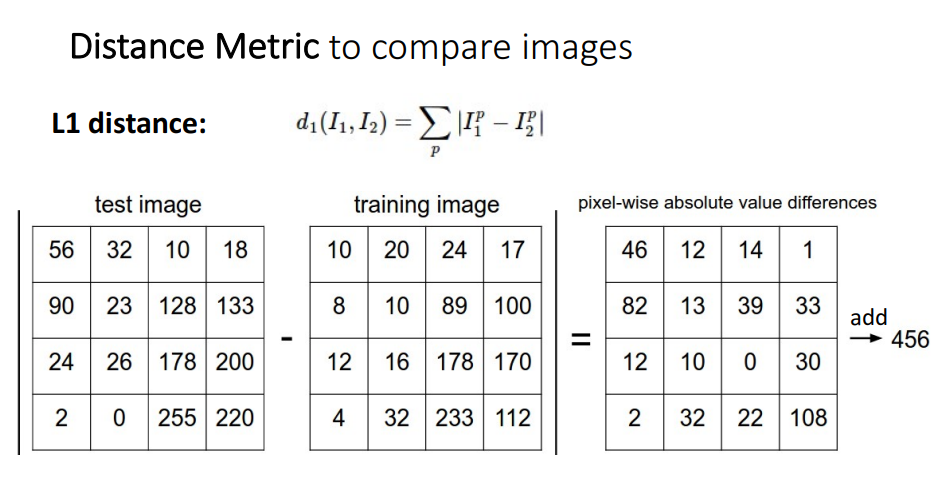
• 거리를 이용하여 유사도를 비교
• 이미지들의 L1(manhattan distance)를 이용해서 픽셀별 차이를 구하고, 차이의 절대값 총합을 구하여 비교
  
• train부분에서는 (n,d)입력 X와 (n,)입력 y
• predict 부분에서는 L1 distance를 이용하여 Ypred를 예측
• 시간 복잡도 차원에서 보면 Big-O 표기법으로
  • train은 O(1)
  • test는 O(N) : 학습 데이터셋이 많을 수록 오래 걸림
• 후에 딥러닝으로 가면 상대적으로 train에서는 많은 시간을 test에서는 적은 시간이 걸린다고 함.

Nearest Decision Boundaries

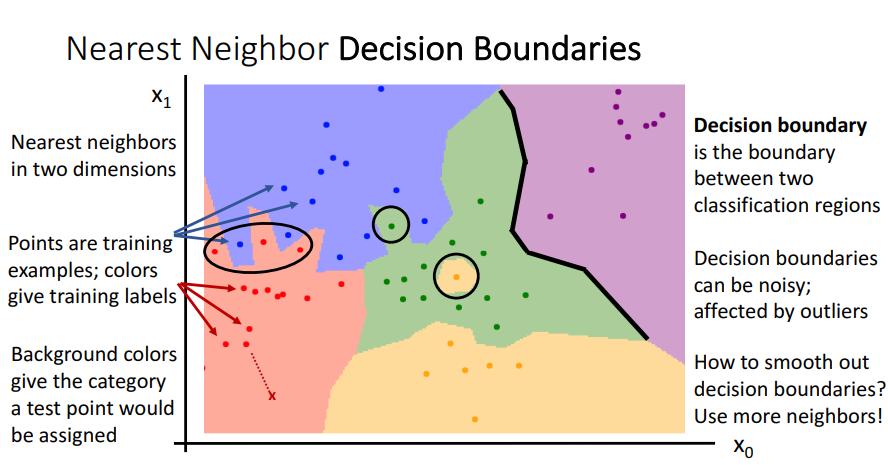
• 2차원에서 Nearest neighbors를 사용
• 각 점들은 training에 사용된 예들이며, 색깔로 라벨링
• 배경의 색을 통해서 카테고리 범위를 확인
• 이상치 때문에 노이즈 발생 가능
  
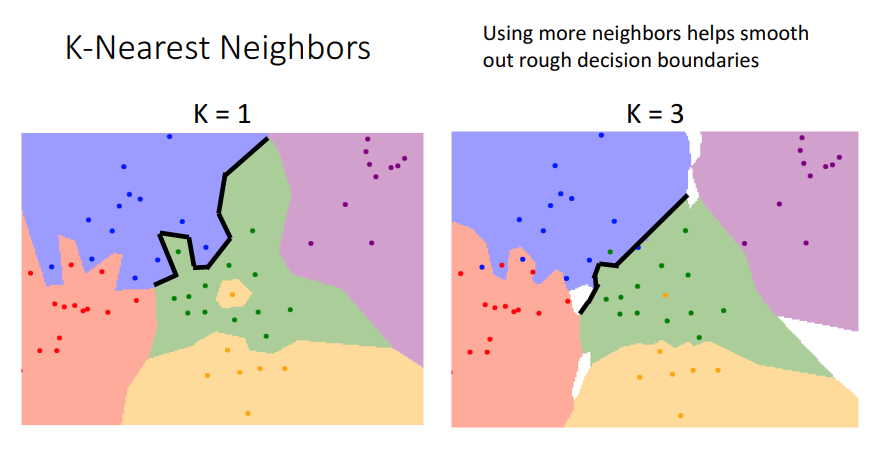
• 이때 K-Nearest Neighbors 알고리즘을 이용하여 1개가 아닌 k개의 가까운 포인트를 찾아 카테고리를 분류하면 더 부드러운 dicision boundaries를 얻음.

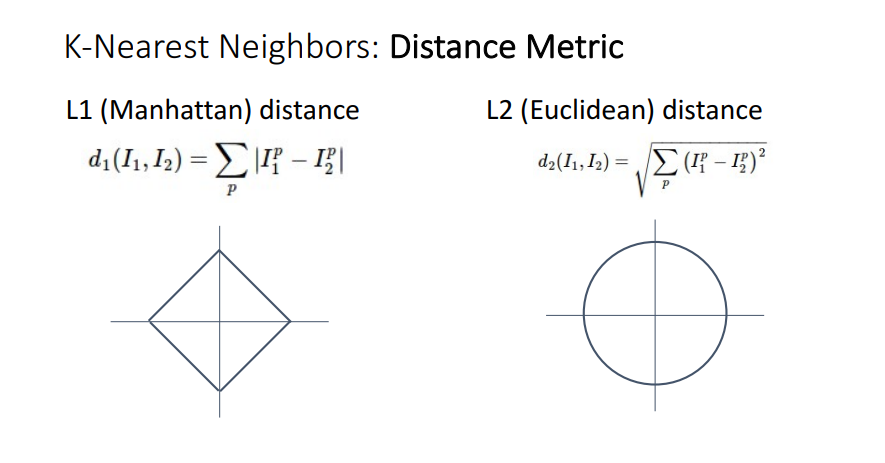
• L1(Manhattan) distance대신 L2(Euclidean) distance를 사용하면 위와 같은 투표 범위가 나타남

• L1 distance로 Nearest Neighbors 알고리즘을 사용하면 수직, 수평 혹은 45각도로 dicision boundaries가 나타남
• L2 distance로 Nearest Neighbors 알고리즘을 사용하면 linear한 dicision boundary이긴 하지만 어느 각도로도 생성 가능.
• Nearest Neighbors 알고리즘을 사용하면 어떠한 데이터가 주어지든 간단해 보이지만 상당히으로 강력한 결과를 낼 수 있음.

Hyperparameters

• Hyperparameters는 training data로부터 학습시킬 수 없고 직접 지정해 주어야 하는 parameters.

• 우리의 데이터에서 가장 좋은 결과를 낼 수 있는 parameters를 결정하는 것이 중요.

• Idea #1
  

  • training set에서 가장 높은 정확도를 보이는 parameters로 지정
  • 최악의 Idea
  • ex) knn의 경우 항상 k=1

• Idea #2
  

  • training dataset과 test dataset으로 분리
  • training dataset으로 학습을 시키고, test dataset으로 정확도 판단
  • 좋지 않은 Idea
  • test dataset에서 정확도를 판단한 이상 test dataset은 이미 사용된 데이터가 됨.

• Idea #3
  

  • training dataset, validation dataset 그리고 test dataset으로 분리.
  • training dataset : 학습을 위해 사용
  • validation dataset : 하이퍼파라미터 적용을 위해 사용
  • test dataset : 마지막 정확도를 위해서 사용

• Idea #4
  

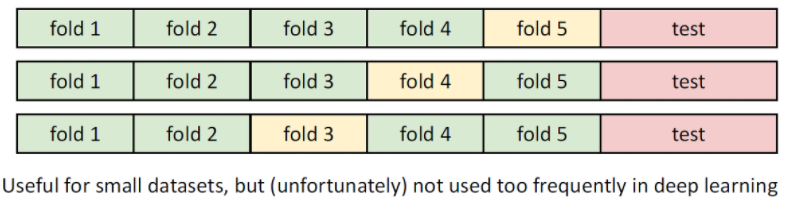
  • dataset을 folds라 불리는 k개의 덩어리와 test dataset으로 분리.
  • k개의 folds가 존재할때 k번을 반복하여 folds를 바꿔가면서 hyperparameter를 결정.
  • 이는 매우 정확한 방법이지만, 매우 많은 연산량을 필요로 하기에 대부분의 머신러닝 프로젝트에서 사용되지 않음.
  • 대신 작은 dataset을 가지거나 연산량을 감당가능할때 사용.
    ![]

K-Nearest Neighbor: Universal Approximation

• K-Nearest Neighbor의 경우 충분한 train dataset이 존재한다면 어떠한 함수라도 표현 가능!

Problem: Curse of Dimensionality

• 차원이 늘어날수록 필요로 하는 training dataset은 지수함수적으로 증가
• 따라서 데이터가 많을수록 좋고, training dataset에 비례해서 추론시간이 걸리는 K-Nearest Neighbor를 raw pixel에 적용한 방식은 현실에서 거의 쓰이지 않음.
  
• 오늘 날에는 deep Network를 이용하여 얻은 Feature Vectors를 K-Nearest Neighbor에 적용하여 문제를 해결

그리고 과제하기...

https://web.eecs.umich.edu/~justincj/teaching/eecs498/FA2020/assignment1.html