Linear Classifiers

• Neural Network는 Lego 블록과 같이 여러 레이어 들을 쌓아 놓은 것
• 이러한 블록들 중에서 가장 기본이 되는 것이 Linear Classifiers.
• Neural Network의 구조가 복잡해 보이지만 개별 구성요소를 살펴보면 Linear Classifiers와 유사

Parametric Approach

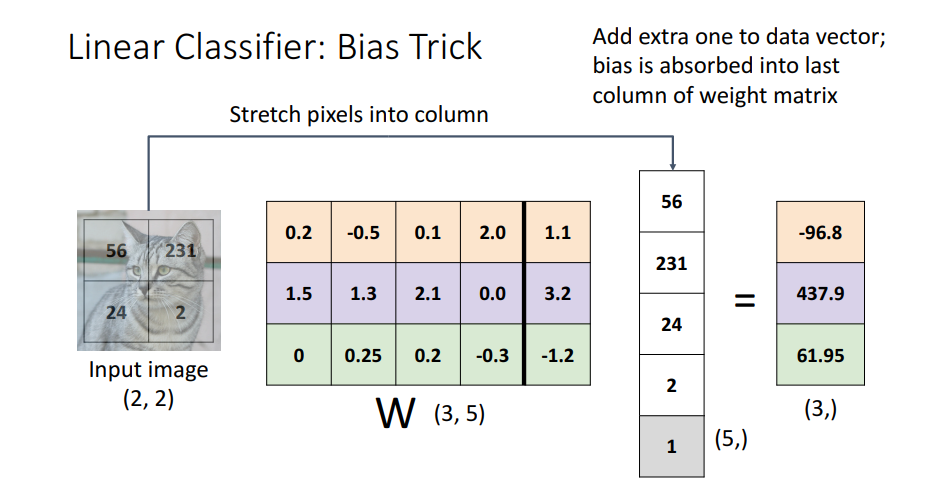
• CIFAR10의 고양이 사진을 예로 들면 32X32X3의 픽셀 사이즈를 가진 x(Input Image)가 있고, 이를 펼쳐주어 3072크기로 변환.

• 이때 (10,3072) shape의 Weight Matrix가 만들어지는데 10은 분류하고 싶은 카데고리 수.

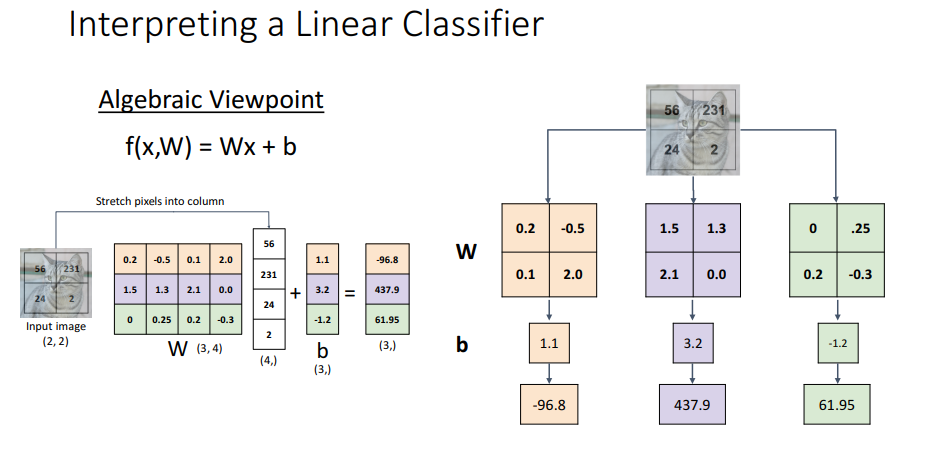
Algebraic Viewpoint

• (10,3072) x (3072,) = 10이 되며 bias(10,)는 우리가 원하는 카테고리에 대한 오프셋 값.
• 이를 다음과 같이 그림으로 표현
  
• 이때 bias를 다음과 같이 W와 x로 한번에 표현가능
  

Visual Viewpoint

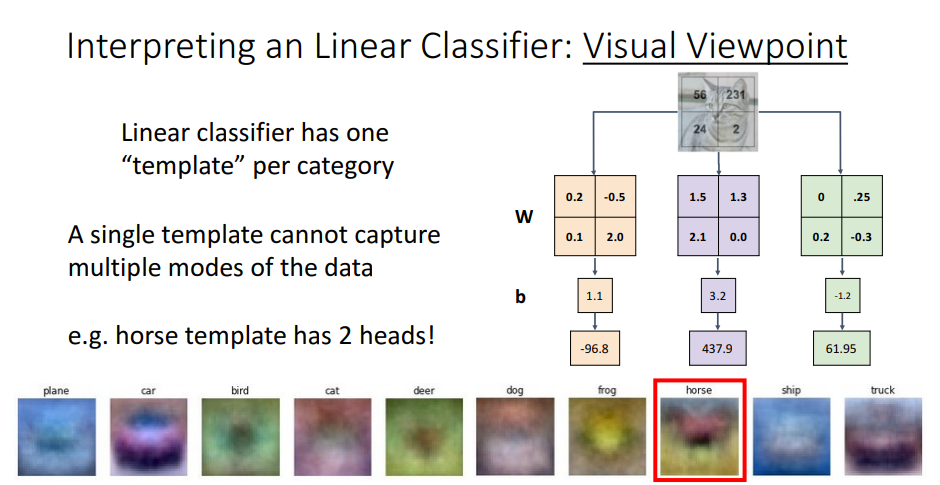
• 또한 linear classifers을 visual viewpoint로 해석 가능
  

• Input 이미지를 펼치고 weight를 (카테고리,이미지 사이즈) 로 만드는것 대신에 원본 input 이미지 shape으로 카테고리수 만큼 개별로 만들어 곱.

• 보다 직관적으로 해석 가능.

• 각 카테고리별 하나의 template만 가지기 때문에 이미지의 다양한 상황 표현 불가능.
  

Geometric Viewpoint

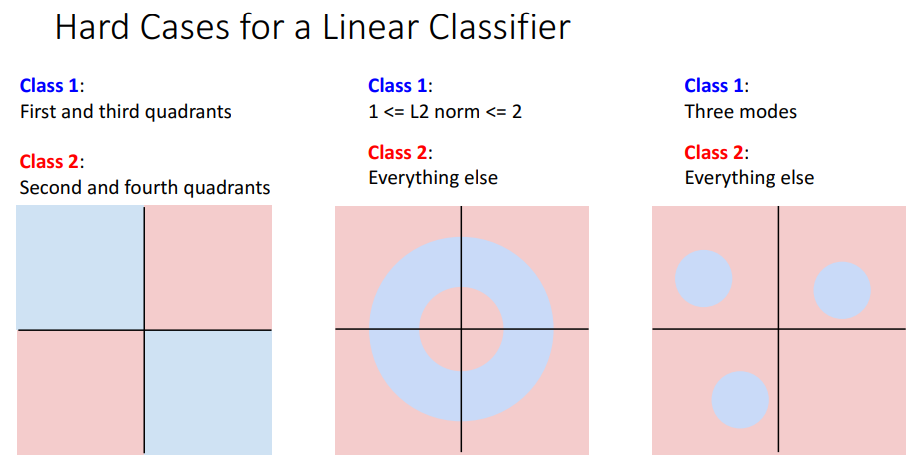
• single pixel
  

• multi pixel
  

• Geometric Viewpoint는 차원이 높기 때문에 때때로 더 직관적이지 못하지만, 그동안 풀 수 없었던 문제에 대한 아이디어 제시
  

• Linear Classifers에서 우리는 W를 통해서 카테고리를 분류할 수 있지만, 알맞은 W를 설정하는법은 배우지 않음.
• 이를 위해서 Loss function을 활용하여 좋은 W 값을 얻는 법을 학습.
• 또한 이를 우리의 학습 데이터에 최적화 시키기 위한 Optimization에 대해 학습.

Loss Function

• loss function은 우리의 classifier가 현재 얼마나 잘 작동하는지 수치로 보여줌.
• loss가 작으면 좋은 classifier
• loss가 높으면 나쁜 classifier
  
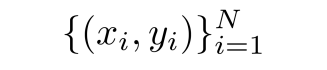
• Dataset은 위와 같이 주어짐.
• x : input image
• y : x의 label

• Loss function은 위와 같이 나타남.
• f(x,W)를 통해서 얻은 value와 x의 label(y)를 비교.
  
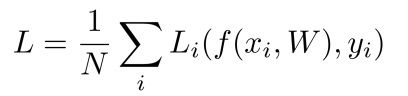
• 평균 Loss function은 위와 같이 나타남.
• input n개에 대한 Loss function의 평균

Multiclass SVM Loss

• 정답 class의 점수는 다른 class의 점수보다 높아야함.
  
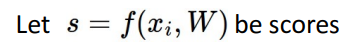
• Function f의 스코어를 s라고 할때
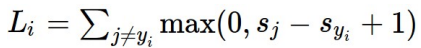
• loss는 위와 같이 계산하며 Li가 일정 값(margin)이하이면 즉, 정답에 대한 s와 다른 클래스의 s의 차이가 일정 margin이상 나면 loss = 0
• Q1. What happens to the loss if the scores for the car image change a bit?
  --> Car의 score가 약간 바뀌어도 다른 클래스의 score에 비하면 차이가 많이 나기 때문에 loss는 계속 0으로 차이가 없을 것!
• Q2. what are the min and max possible loss?
  --> min loss의 경우 0이고, max loss의 경우 무한대.
• Q3. If all the scores were random, what loss would we expect?
  --> scores가 가우시안 분포를 따르고 0에 가까운 매우 작은 수라고 가정했을 때 카테고리의 수를 C라고 하면 이므로 (C-1) X margin이고 위의 식의 경우에서는 (C-1) X 1
• Q4. What would happen if the sum were over all classes? (including i = yi)
  --> 합계가 모든 클래스에 적용되면
  
  식에 따라서 1이 증가할 것.
• Q5. What if the loss used a mean instead of a sum?
  --> 합 대신 평균으로 바꾼다고 해도 단조변화이기 때문에 loss의 변화는 있지만 weight의 변화는 없을 것.
• Q6. What if we used this loss instead?
  
  --> loss function 자체가 바뀌므로 더이상 multi-class SVM이라 부를 수 없고 loss값 역시 완전히 달라지게 됨.
• Q7. Suppose we found some W with L=0. Is it unique?
  --> No!, 가중치를 2배로 바꿔주어도 여전히 L=0이 나옴.
• Q8. How should we choose between W and 2W if they both perform the same on the training data?
  --> training data셋에서 같은 loss값을 가지더라도 Weight 값은 여러개 존재 가능. 따라서 여러 Weight 값중 최적의 Weight를 선택하기 위한 추가방법이 필요.

Regularization: Beyond Training Error

• Regularization은 training dataset에 과적합하게 학습되는 것을 방지.
• Loss function에 추가적으로 Regularization 항을 더하여 사용.
• Regularization은 lambda라고 불리는 하이퍼파라미터와 함께 사용되는데 lambda를 통해서 Regularization의 정도를 조절.
• Regularization은 L2,L1 Elastic net과 같은 것들이 존재하며 Neural Network에서 Dropout, Batch normalization등이 다양한 기법이 사용됨.
• Regularization을 써야하는 이유는 크게 3가지
  • 모델간의 선호도 표현
    
  • 과적합 방지
  • 곡률 추가를 통한 최적화 개선

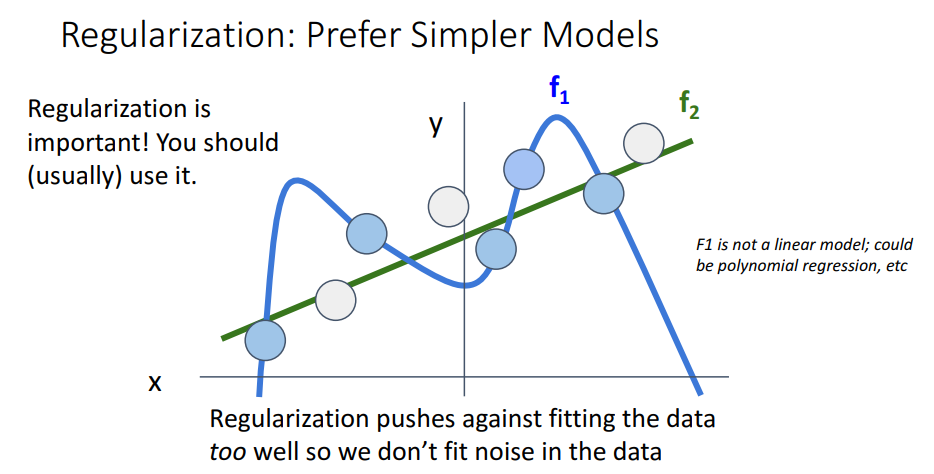
• 파란색의 경우 training dataset에 맞게 복잡한 function으로 나타내고 있고, 초록색의 경우 보다 덜 복잡하게 나타냄.
• training dataset뿐만 아니라 한번도 보지 못한 test dataset을 추론하기 위해서는 이상치를 모두 고려하는 복잡한 모델보다는 일반적인 모델이 더 좋은 성능이 나올 수 있음.

Cross-Entropy Loss( Multinomial Logistic Regression)

• 최근 가장 흔하게 사용됨.
• Cross-Entropy Loss는 score를 확률로 해석하기 위해 softmax라는 함수를 사용
  

1. 주어진 score들을 지수화 시켜 음수값 제거
2. softmax함수를 이용 --> normalize시켜서 확률분포를 계산
3. 이를 Kullback_leigler divergence라는 것을 통해 확률분포와 correct class 비교.

• Q1. What is the min/max possible loss Li?
  --> min : 0, max : infinity
• Q2. If all scores are small random vlaues, what is the loss?
  --> score들이 0에 가깝다면 지수화 시켰을때 1이 되므로 loss = -1/log(C)