Optimization

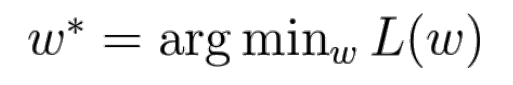
• Optimization의 목표
  : Loss Function에 Input으로 weight matrix를 넣어주었을때, 가장 작은 Loss값을 가지게 하는 weight matrix 찾기
  
• 직관적으로 이해하기
  • 땅의 x,y 좌표를 weight matrix의 w라고 생각하고 그 지점에서의 높낮이를 Loss라고 가정
  • 장님의 사람이 횡단을 한다고 가정
  • 이 사람은 방향감각도 없고, 어디가 가장 낮은 부분인지도 인지 X
  • 이 사람이 이 지역에서 가장 낮은 부분을 찾을 수 있도록 도와야함

• Idea #1 : Random Search

  • 무작위로 weight matrix를 매우 많이 만들고 그 중에서 가장 낮은 loss를 가지는 weigth matrix를 선택

• Idea #2 : Follow the slope

  • 장님이 사람이 횡단을 한다고 가정
  • 앞은 보이지 않아도 어느 방향으로 경사가 져있는지는 확인 가능
  • 어느 방향으로 경사가 져있는지 오직 local 정보만을 활용

  

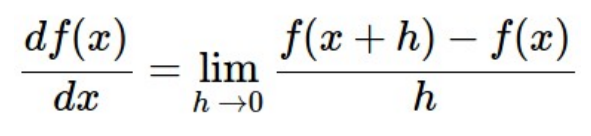
  • 이를 공식화 하면 현재 위치 x에서의 기울기를 통해 진행 방향 결정

  

  • Numeric gradient
    • 현재 Weight matrix에서 weight를 h만큼 변경했을때, loss의 변화를 통해 gradient를 얻음
    • 이 방법은 실제 사용하기에는 파라미터가 많아질수록 너무 느리고, 실용적이지 않음
  • Analytic gradient
    • 하나씩 w를 돌면서 gradient를 얻는 것이 아니라 gradient 도출 식만 얻어 한번에 계산
    • 정확하고 빠름

• 실제로는 analytic gradient를 주로 쓰지만 numerical gradient를 디버깅 툴로 활용

• gradient check라고 불리는 확인 과정을 거침

• pytorch 에서는 gradcheck와 gradgradcheck라는 함수를 통해 확인

Gradient Descent

• loss function을 optimizing하기 위한 전략으로 우리는 어느 지점에서 시작을 하고, 그 지점에서 gradient를 구해 loss가 줄어드는 방향으로 이동 후 이 과정을 반복.
• 매우 간단한 알고리즘
• Gradient Descent에 사용되는 Hyperparameters

  • Weight initialization method

    • weight를 초기화를 할때 어떻게 초기화를 하느냐에 따라서 결과가 달라짐

  • Number of steps

    • 여기에는 여러가지 stopping criteria가 있지만 딥러닝에서 가장 흔하게 쓰이는 방법은 단순하게 지정해주는 것

  • Learning rate

    • 한번에 얼마나 움직일 것인지를 결정
    • 얼마나 빠르게 학습 시킬것인지를 결정

    

• Gradient Descent를 heatmap으로 살펴보면 loss function이 그릇 형태로 되어있고, 빨간색에서 low loss를 가짐.
• w Matrix의 진행방향은 가장 low한 지점으로 바로 가는 것이 아니라 경사를 따라서 곡선 형태로 진행.

Batch Gradient Descent

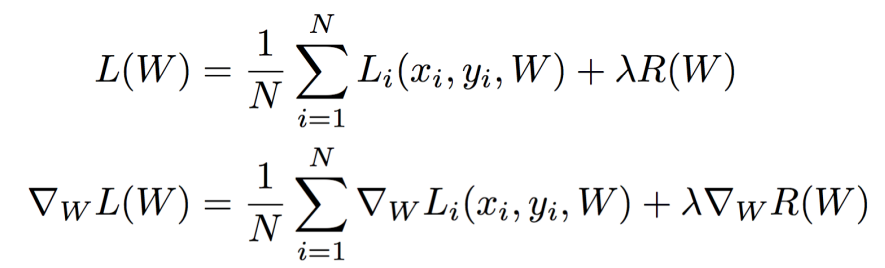
• Batch Gradient Descent 혹은 Full Batch Gradient Descent라고 불림.
• 데이터가 커지면 gradient의 계산 역시 오래걸려 한스탭을 진행하려고 오랜시간을 기다려야 할 수 있음.

Stochastic Gradient Descent (SGD)

• 전체 데이터셋를 학습을 하기 보다 전체 데이터셋에서 mini batch라고 불리는 일부분을 샘플링해서 loss와 gradient를 대략적으로 학습.
• Gradient Descent에서 Weight initialization method, Number of steps, Learning rate와 함께 batch size도 하이퍼 파라미터로 지정.
• 주로 GPU 성능에 따라서 batch 사이즈를 결정하고, GPU 성능이 좋을수록 batch 사이즈를 크게 가져감.
• classification 문제에서는 그다지 중요하지 않을 수 있지만, prediction, matching 또는 ranking 문제에서는 중요할 수 있음.

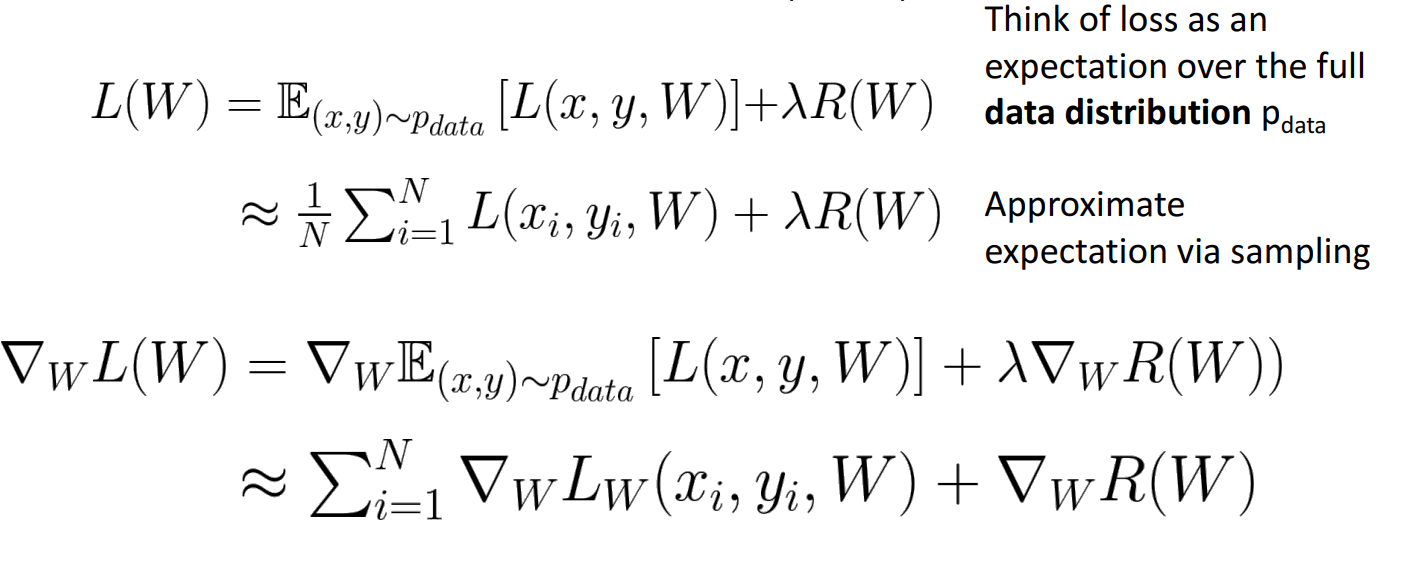
• 샘플링 된 데이터가 전체 데이터와 유사하도록 샘플링을 해야함

Problems with SGD

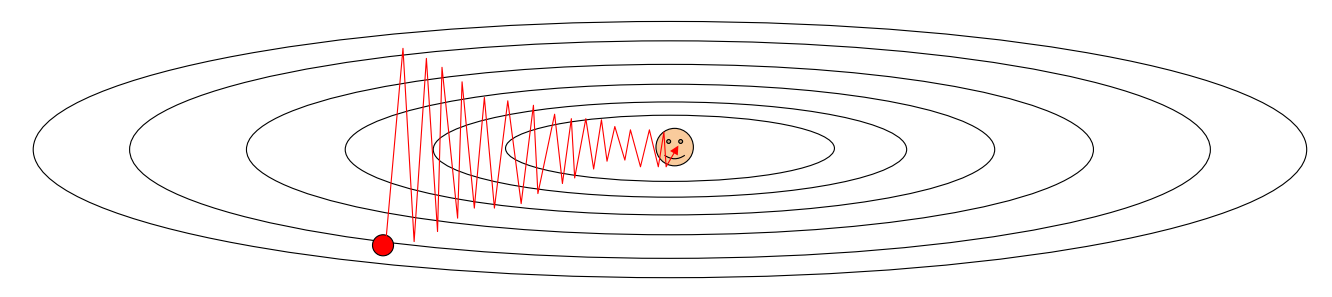
• What if loss changes quickly in one direction and slowly in another?
  • w의 스텝이 크면 zigzag로 이동할 수 있고 오히려 더 많은 학습 시간이 걸릴 수 있음
  • 이 때문에 overshooting에도 취약
  • w의 스텝 사이즈를 매우 작게 하여 overshooting을 예방할 수 있지만 시간이 매우 오래 걸림.

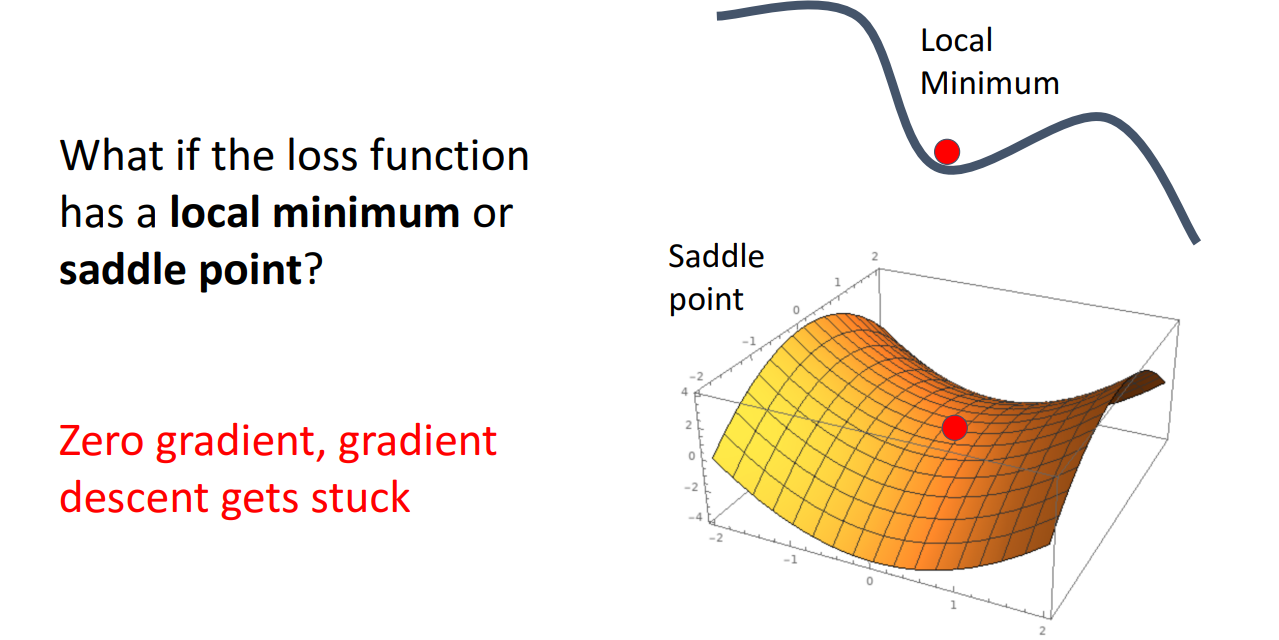
• What if the loss function has a local minimum or saddle point?
  • 함수가 커지다가 작아지는 순간 역시 0의 gradient를 가짐 (saddle point)
  • gradient가 0이지만 함수의 최소값을 가짐 (local minimum)
  • 차원이 커질수록 local minimum과 saddle point가 더 빈번하게 발생

• full batch가 아닌 mini batch를 사용하기 때문에 경로에 noisy가 발생

위와 같은 문제점들을 극복하기 위해서 실제로는 그냥 SGD를 사용하기 보다 더 똑똑한 버전을 사용하여 모델을 학습.

SGD + Momentum

• 언덕에서 공을 굴리는 것으로 생각
  • 매순간 공의 속도를 계산
  • 이때 공의 현재 속도 뿐 아니라 이전의 공의 속도 또한 반영
  • rho라고 불리는 마찰 혹은 감쇠율 하이퍼 파라미터를 활용해서 속도를 계산
  • rho는 이전의 공의 속도를 얼마나 반영해줄지 결정, 대체로 0.9 or 0.99
  • 공의 속도가 빠르면 현재 local gradient가 공의 진행 방향과 반대라고 하더라도 공은 굴러감

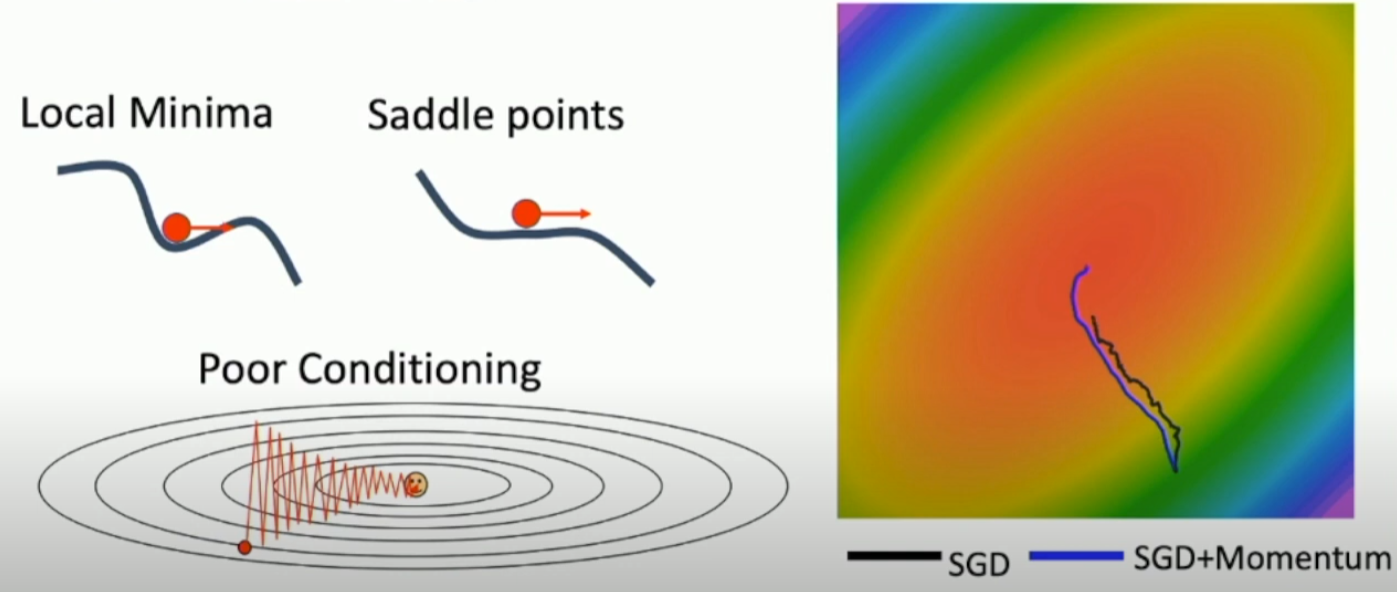
SGD + Momentum을 사용하면 loss가 최소값이 아니지만 gradient는 0인 Local Minimal과 Saddle points, 한쪽 방향의 경사가 급격하여 지그재그로 움직이는 Poor Conditioning 문제를 어느정도 해결

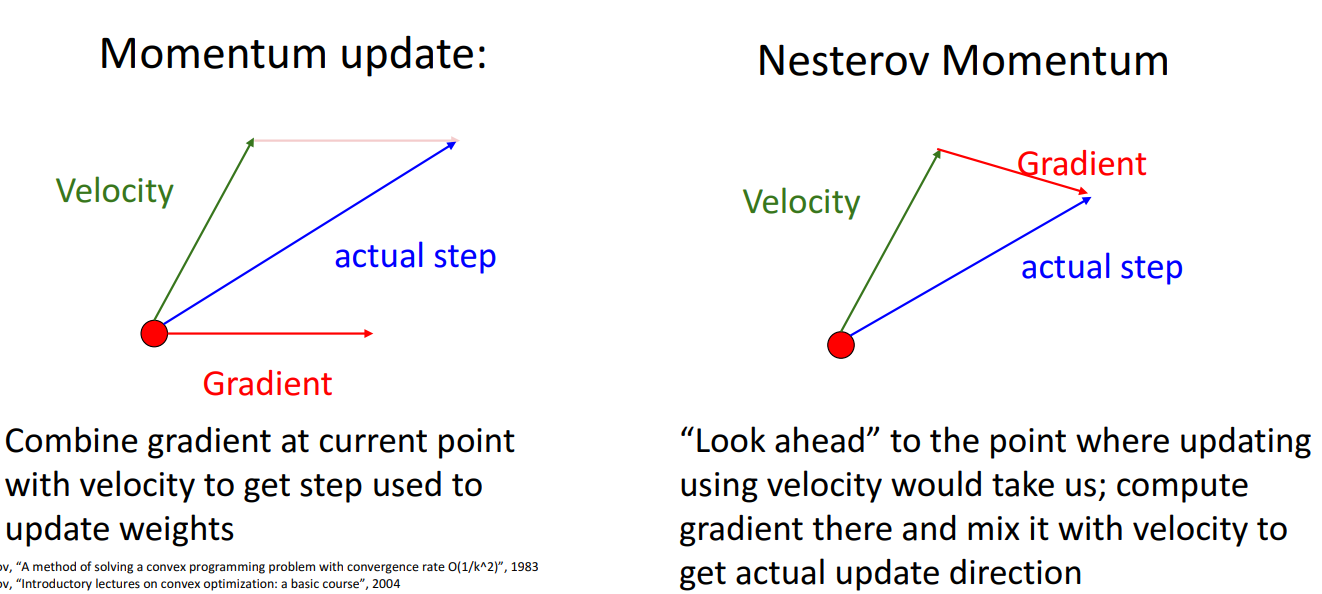
Nesterov Momentum

• 기존 Momentum 업데이트 방식은 이전까지의 속도와 현재 위치에서 gradient를 더해주어 업데이트
• Nesterov Momentum의 경우 이전까지의 속도와 이전까지의 속도를 진행한 위치에서의 gradient를 더해주어 업데이트
  

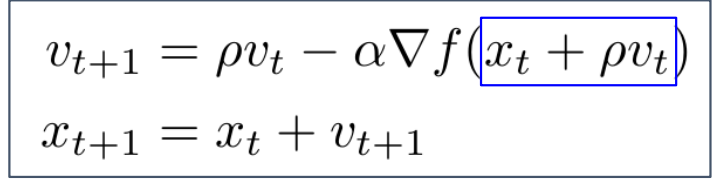
• SGD, SGD+Momentum, Nesterov 이 세가지를 그림을 통해서 비교
• SGD+Momentum과 Nesterov는 velocity를 사용했기에 overshooting가 발생

AdaGrad

• SGD을 Momentum과는 다른 방식으로 변형
• gradient 값을 사용하는 것 대신에 gradient 값의 제곱을 사용
• gradient 값의 제곱을 누적해서 합(grad_squared)을 구하고 learning rate에 grad_squared의 제곱근으로 나눠 줌
• gradient의 변화가 큰 부분에서는 큰 값(grad_squared.squart())으로 나누어줘서 속도를 줄임
• gradient의 변화가 작은 부분에서는 작은 값(grad_squared.squart())으로 나눠줘서 속도를 높임
• 학습을 오래 하면 gradient 값의 누적합(grad_squared)이 무한히 커지기 때문에 learning rate이 0이 되어 멈춤

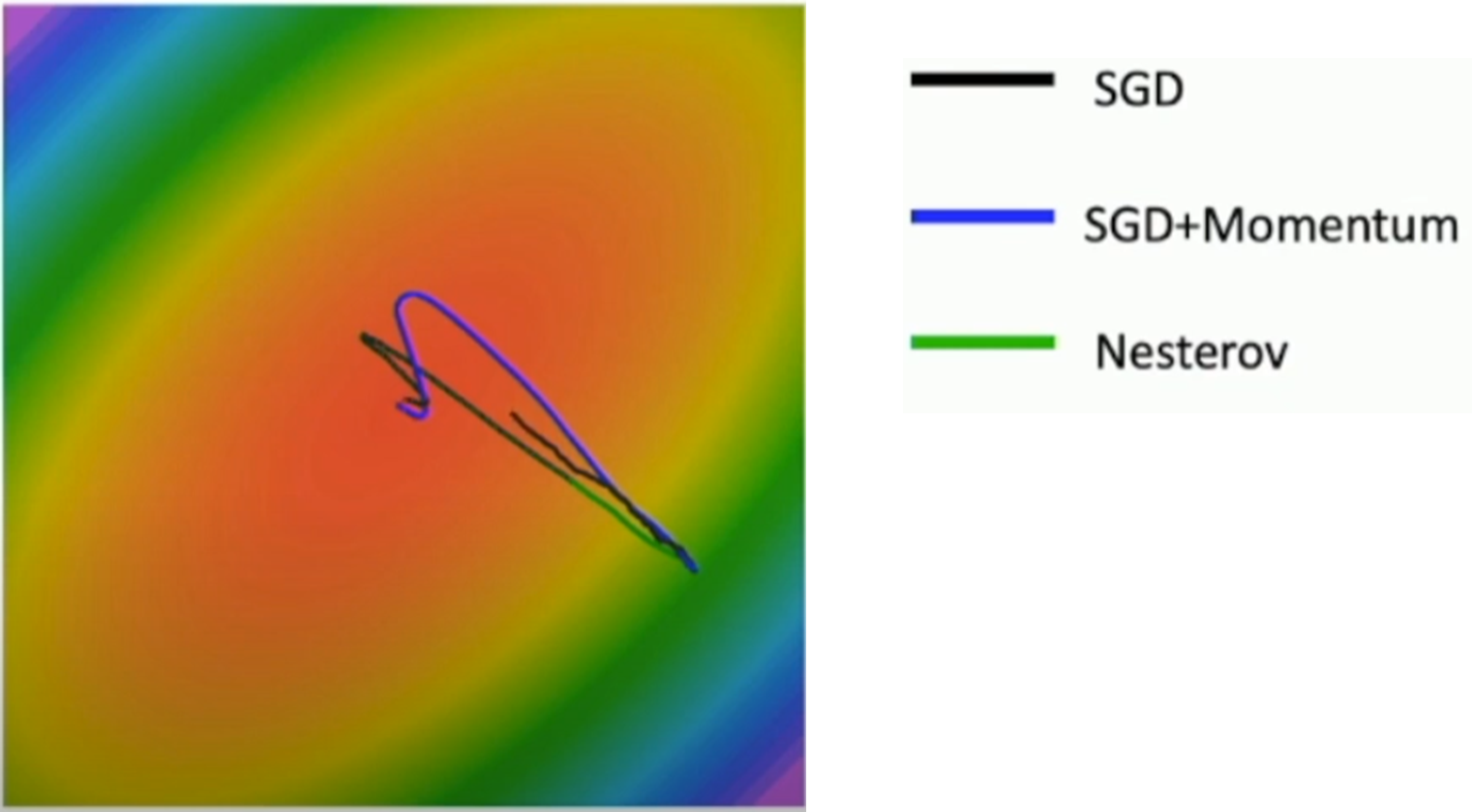
RMSProp: "Leak Adagrad"

• AdaGrad에서 학습을 오래 하면 진행이 멈추는 것을 극복하기 위해서 고안
• SGD + Momentum에서 rho를 통해 속도를 조절하는 것과 비슷하게 일종의 friction을 추가 (decay_rate)

• SGD+Momentum의 overshooting문제를 해결

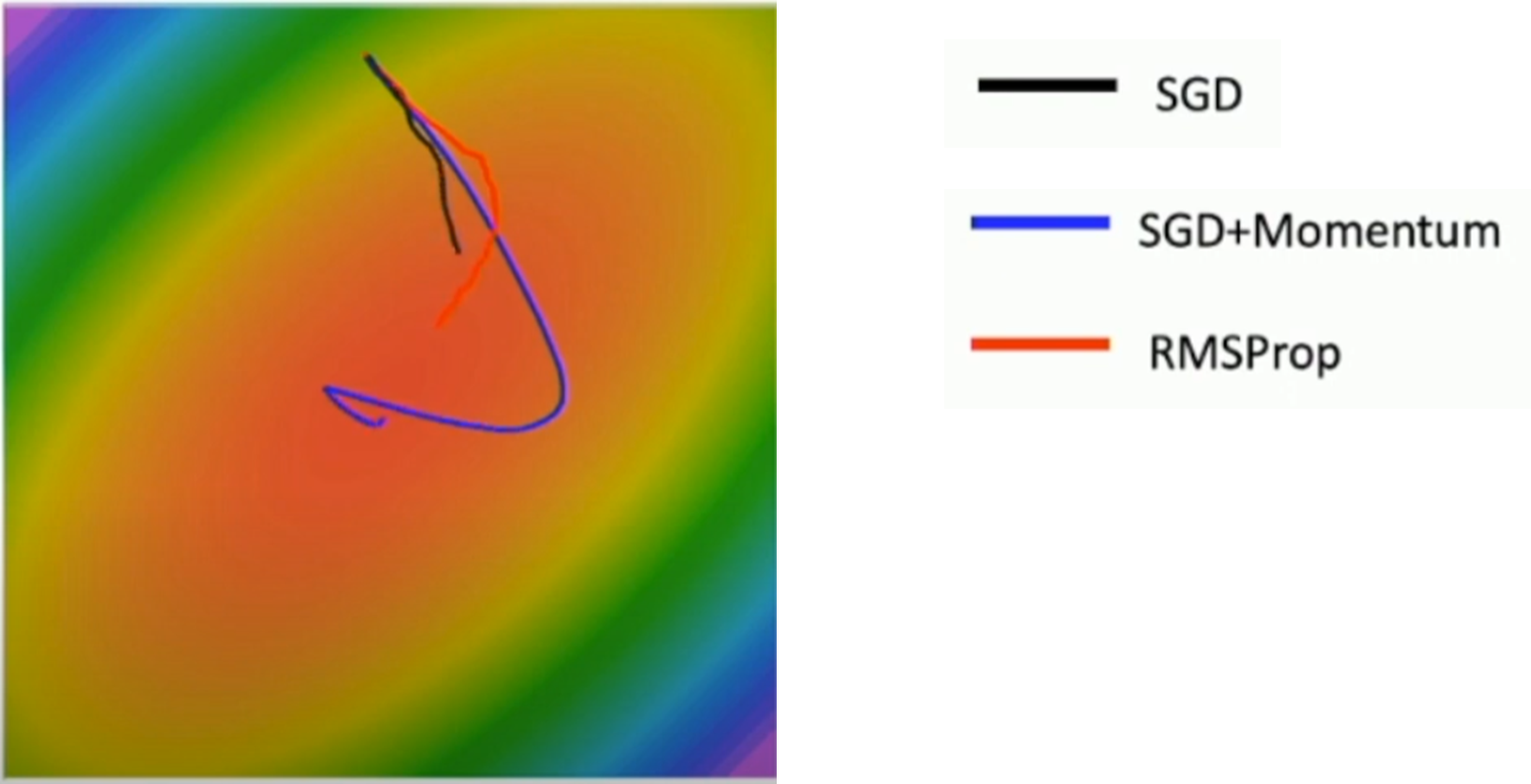
Adam : RMSProp + Momentum

• RMSProp와 Momentum을 합친 알고리즘

• t = 0일 때, beta2 = 0.999로 1에 가까운 값이라고 가정하면, moment2가 0에 가까워지고 제곱근을 취하여 나누어 주면 w가 매우 큰 값이 나올 수 있는 문제가 발생

• 따라서 위와 같이 Bias correction을 통해서 이를 방지
• 실제로 Adam을 사용할때 beta1 = 0.9, beta2 = 0.999, learning rate = 1e-3,5e-4,1e-4일 때 좋은 결과를 낸다 함.
• 지금까지 배운 optimizer들을 비교하면 다음과 같음.

.

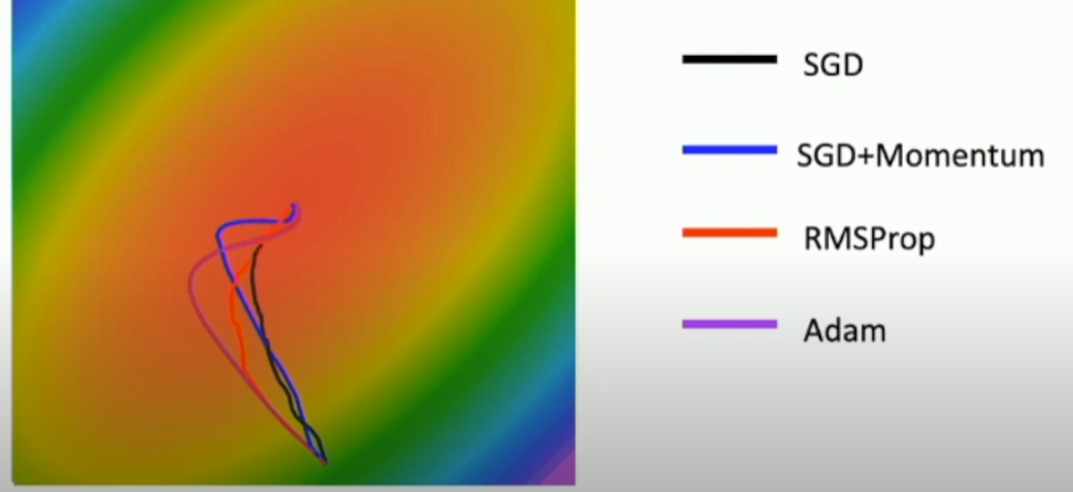
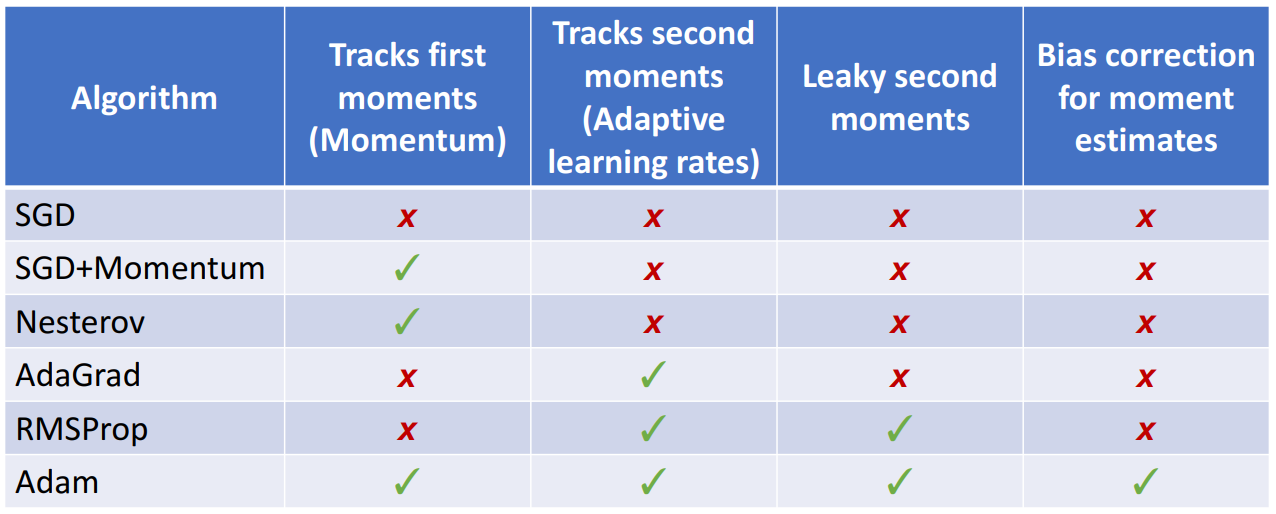
• 실제로는 대부분의 상황에서 Adam을 사용하고 SGD+Momentum 역시 조금 고치면 Adam보다 좋은 성능을 낼 수도 있다함.
• full batch를 사용할 수 있으면 L-BFGS를 사용하는 것도 방법이 될 수 있음