1-4 편향과 분산

Training data vs Test data

데이터의 분할

• 입력된 데이터는 학습 데이터와 평가 데이터로 나눌 수 있음
• 학습 데이터는 모델 학습에 사용되는 모든 데이터셋
• 평가 데이터는 오직 모델의 평가만을 위해 사용되는 데이터셋
• 평가 데이터는 절대로 모델 학습에 사용 X

평가 데이터

• 학습 데이터와 평가데이터는 같은 분포를 가지는가? 랜덤함수를 통해서 분류 --> 거의 비슷
• 평가 데이터는 어느정도 크기를 가져야 하는가? 10% ~ 20%

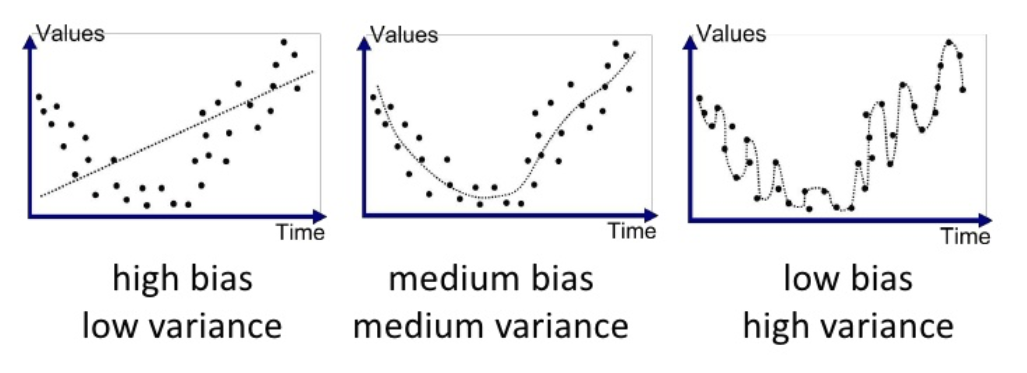
모델의 복잡도

• 선형에서 비선형 모데롤 갈수록, 복잡도가 증가함
• 모델이 복잡해질수록, 학습 데이터를 더 완벼하게 학습함
• 모델의 복잡도에 따른 결과
  • 모델의 복잡도가 너무 작은 경우 Under-fitting 문제 발생
  • 모델의 복잡도가 너무 큰 경우 Over-fitting 문제 발생

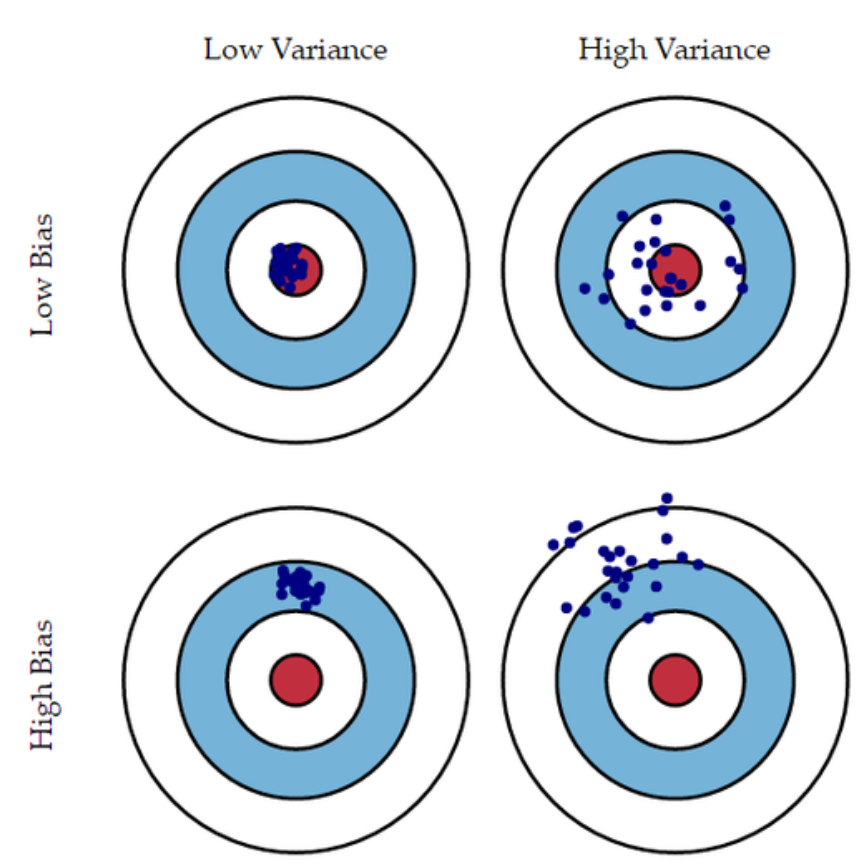
편향(bias)과 분산(variance)

• 편향과 분산은 모두 알고리즘이 가지고 있는 에러의 종류
• $MSE(\hat\theta) = E_\theta((\hat \theta -\theta)^2) = E_\theta((\hat \theta - E(\hat \theta) + E(\hat \theta)- \theta)^2)$
  $= E((\hat \theta - E(\hat \theta))^2 + 2(\hat \theta - E(\hat \theta))(E(\hat \theta)- \theta)+(E(\hat \theta)- \theta))^2)$
  $=E((\hat \theta-E(\hat\theta))^2)+(E(\hat\theta) - \theta)^2$
  $=Var(\hat\theta)+Bias(\hat\theta,\theta)^2$
• 즉 variance는 {예측값과 (예측값들의 평균값)의 오차제곱합}의 평균
• 편향은 예측값들의 평균값과 정답 값의 차이
• 편향은 정답과 예측값들의 평균값만 비교를 하기 때문에 under-fitting과 관련
  • ex 예측 값들이 넓게 분포되어 있어도 평균만 정답값과 비슷하면 성능 좋다고 판단
• 분산은 예측값과 예측값들의 평균값의 오차제곱합이므로 데이터셋이 달리짐에 따라서 크게 변동성이 있는 overfitting과 관련
  
  
  

• 모델 복잡도를 키우면서 과적합을 막는 방법론을 사용

1. 검증 데이터셋을 활용
2. K-fold cross validation
3. 정규화 손실 함수

검증 데이터셋

• 모델 학습의 정도를 검증하기 위한 데이터셋
• 모델 학습에 직접적으로 참여하지 못함
  
• test 데이터셋과 validation 데이터셋은 학습에 직접 참여는 하지 못하지만
• test 데이터셋과 달리 validation 데이터셋은 학습 중간에 평가를 하고 가장 좋은 성능의 파라미터 지정

Leave-One_Out Cross-Validation(LOOCV)

• 랜덤으로 생성된 검증 데이터셋 하나는 편향된 결과를 줄 수도 있음
• 검증 데이터셋에 포함된 샘플들은 모델이 학습할 수 없음
• 간단하게 모든 데이터 샘플에 대해서 검증을 진행할 수 있음
  
  

K-fold cross validation

• LOOCV의 경우 계싼 비용이 매우 큰 단점

• 이러한 문제를 해결하기 위해, K개의 파트로 나누어 검즘을 진행하는 방법
  

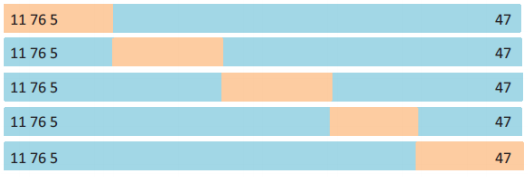
• K가 커지면

  • 학습 데이터의 수 작아짐(validation 데이터가 적어지기 때문)
  • Bias 에러값 작음, variance 에러값 커짐(들쑥날쑥)
  • 계산 비용 커짐

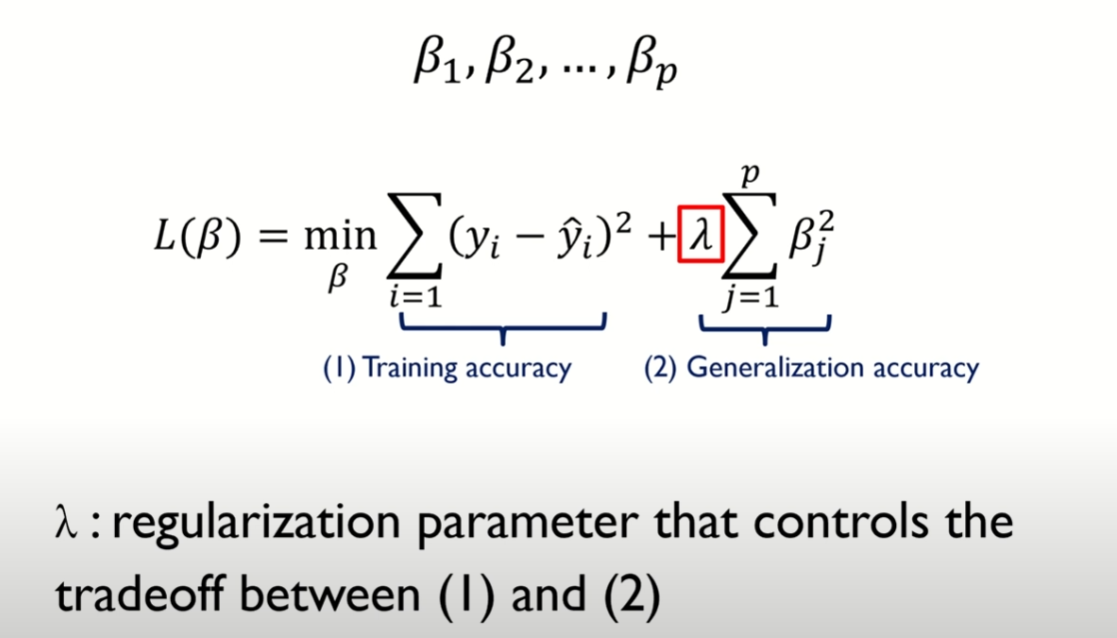
Regularization (정규화)

• 정규화 손실 함수
  • 모델의 복잡도가 커진다 == 모델의 파라미터 수가 많아진다
  • 모델의 복잡도가 커질수록, 과적합(over-fitting)이 발생할 가능성이 커진다
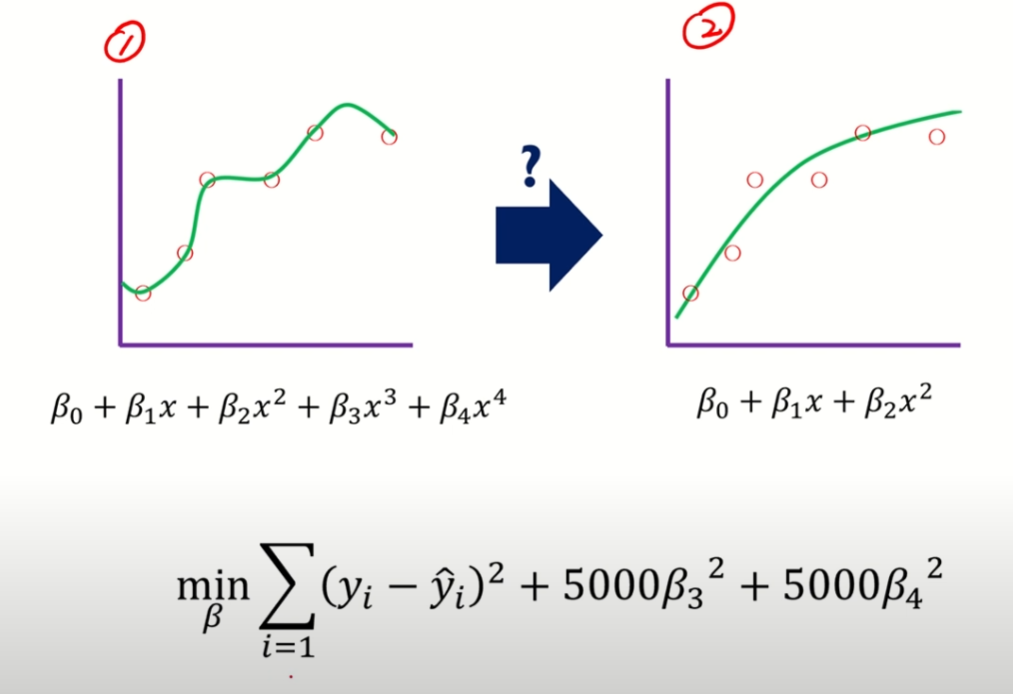
  • 1. 복잡도가 큰 모델을 먼저 정의하고, 2. 그 중 중요한 파라미터만 학습하면 안될까?
  • 필요없는 파라미터 값을 0으로 만들자
• 정규화 종류
  • Ridge 회귀(L2 regression)
  • Lasso 회귀(L1 regression)

Ridge Regression

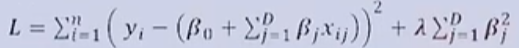
• MSE 손실을 줄이지 못하면 페널티 항의 손실값이 더 크게 작용함
• $\lambda$(람다)는 정규화의 영향을 조절하는 하이퍼파라미터
• 정규화 식이 제곱의 합으로 표현됨
  
  

Lasso Regression

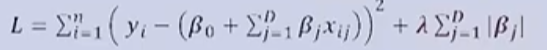
• MSE 손실을 줄이지 못하면 페널티 항의 손실값이 더 크게 작용함
• $\lambda$(람다)는 정규화의 영향을 조절하는 하이퍼파라미터
• 정규화 식이 제곱의 합으로 표현됨

$\lambda$(람다)가 커지면 Bias 에러값이 커지고, Variance 에러값이 작아짐
파라미터의 희소성(sparsity)정도 : Ridge 정규화 < Lasso 정규화
0의 값을 가진 파라미터가 더 많아지게 하는 방법? 람다 증가

출처 :
https://www.youtube.com/watch?v=pJCcGK5omhE&t=21s
https://www.youtube.com/watch?v=oyzIT1g1Z3U&list=PL7SDcmtbDTTylCwjSDzGduvR-1EItFF2X