2-1 Logistic Regression

회귀 (Regression)

• Input : 연속값(실수), 이산값(범주형) 등 모두 가능
• output : 연속값(실수형)
• 모델 형태 : 일반적인 함수 형태( ex. $y = w_1x+w_0)$

분류 (Classification)

• Input : 연속값(실수형), 이산값(범주형) 등 모두 가능
• Output : 이산값(범주형)
• 모델 형태
  • 이진 분류 --> sigmoid 함수 적용 ($\sigma(y))$
  • 다중 분류 --> softmax 함수 적용

Why not Linear Regression?

• 위와 같이 라벨링을 해주었을 경우 라벨의 순서(1,2,3)에 따라서 결과가 달라짐
  --> 라벨링에 따라서 loss가 상대적으로 커지거나 작아질 수 있어서 학습에 영향
• 다른 손실 함수나 모델이 필요

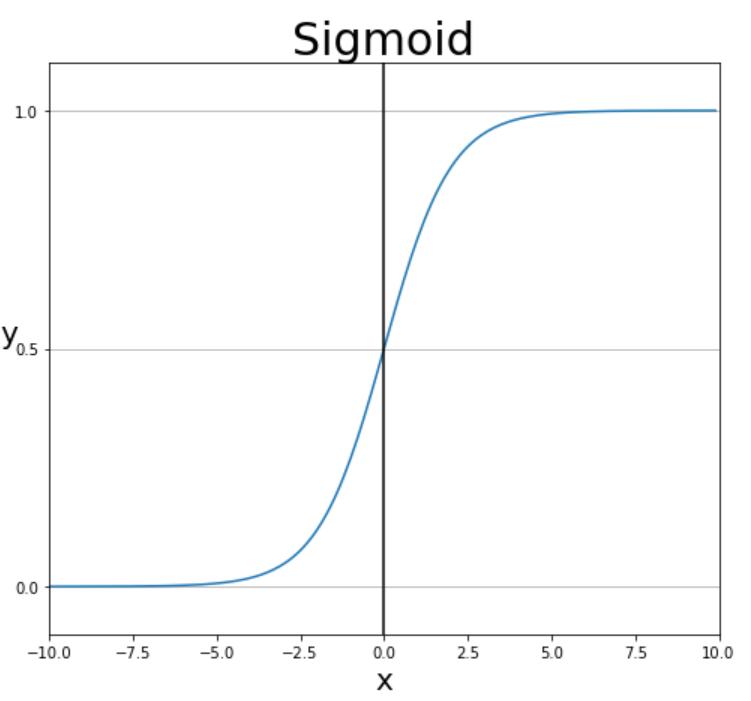
Sigmoid Function

• $y = \frac{1}{1+e^{-x}}$
• x = 0 일때, 함수의 출력값은 0.5가 됨
• 함수의 출력값이 항상 0이상 1이하임
  

오즈(odds)

• 성공 (y=1)확률이 실패(y=0) 확률에 비해 몇 배 더 높은가를 나타냄
• $odd = \frac{p(y=1|x)}{1-p(y=1|x)}$

로짓 변환(logit)

• 오즈에 로그를 취한 함수 형태
• 입력값 (p)의 범위가 [0,1] 일 때, [-$\infin$,+$\infin$] 를 출력함
• $logit(p) = log(odds) = log\frac{p(y=1|x)}{1-p(y=1|x)}$
• p = $\frac{1}{2}$ 일때 logit = 0

logistic function

• 로짓 변환의 역함수로 해석 가능
• $logit(p) = log(odds) = log\frac{p(y=1|x)}{1-p(y=1|x)} = W_0 + W_1X_1 + ... + W_DX_D = W^TX$
• logit(p)는 [$-\infin,\infin$] 사이의 값을 가지고, 이를 W와 X라는 파라미터를 통해서 선형함수처럼 표현
• 그리고 W와 X에 대한 행렬곱으로 표현 = $W^TX$
• $p(y=1|x) = \frac{e^{W^TX}}{1+e^{W^TX}} = \frac{1}{1+e^{-W^TX}}$
• 따라서 로지스틱 함수는 linear regression과 sigmoid 함수의 결합

logistic Regression

• logistic function 형태의 회귀 모델
• P($\hat y=1|X) = \frac{1}{1+e^{-W^TX}}$
• $W^TX$의 값에 따라 예측이 달라짐

1. $W^TX$ > 0 : 1로 분류
2. $W^TX$ < 0 : 0으로 분류

손실함수는 어떻게 정의??

• optimizer인 SGD를 사용하기 위해서는 $\frac{\partial L}{\partial \omega}$를 알아야하고 Loss Function의 정의가 필요
• 기존 MSE의 경우 Regression을 위한 loss function
• 따라서 classification을 위한 loss function 필요

Bayes' Theorem

• 베이즈 정리는 사건 B가 발생함으로써(사건 B가 진실이라는 것을 알게 됨으로써, 즉 사건 B의 확률 P(B)=1이라는 것을 알게 됨으로써) 사건 A의 확률이 어떻게 변화하는지를 표현한 정리
  --> B가 일어났을 때, A의 확률 변화 표현
• $P(W|X) = \frac{P(X|W)P(W)}{P(X)}\propto P(X|W)P(W)$
• 사전 확률(prior, P(W)) : 데이터를 보기 전, 일반적으로 알고 있는 가설의 확률
  --> 일반적으로 W가 일어날 확률
• 우도 확률(likelihood, P(X|W)) : 가설을 잘 모르지만 안다고 가정했을 경우, 주어진 데이터의 분포
• 사후 확률(posterior, P(W|X)) : 데이터가 주어졌을 때 가설에 대한 확률 분포(신뢰도)
  --> X가 일어났을 때, W가 일어날 확률
  -->사전 확률과 우도 확률의 곱에 비례

• 이 확률들을 통해 가설(모델의 파라미터)를 추정하는 방법으로 MLE와 MAP 두 가지가 있음

Maximum Likelihood Estimation

우도 확률(likelihood, $P(X|W))$

• 모델의 파라미터값(W)를 잘 모르지만 안다고 가정했을 경우, 주어진 데이터의 분포
• 우도 확률은 모델의 파라미터 (W)에 대한 함수로 데이터의 분포를 표현함
• 각 샘플이 i.i.d(independent and identical distributed)하다고 가정 후, 흔히 아는 PDF(probability density function)의 곱으로 표현
• i.i.d는 각각의 random variable이 독립적이고, 같은 확률분포를 가질때 사용
• PDF는 확률분포 함수
• Ex. 정규 분포를 따르는 데이터에 대한 우도 확률
  • W : $\mu$(평균), $\sigma$(분산)
  • PDF : $\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}(\frac{x-\mu}{\sigma})^2}$
  • Likelihood : $\Pi_i\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}(\frac{x-\mu}{\sigma})^2}$
    --> 모든 데이터셋의 PDF에 대한 곱셈

• 확률 : 확률 분포(정규분포)는 고정되어 있고, X의 변화에 따라서 확률이 달라짐
• 우도 확률(likelihood) : X는 고정되어 있고, 확률 분포의 변화에 따라서 우도 확률이 달라짐.
  

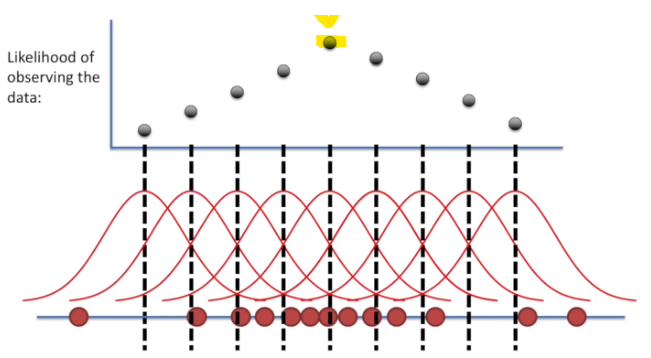
최대 우도 추정법(MLE)

• 현재 데이터 분포가 나올 확률이 가장 높은 파라미터 == 우도 확률을 최대로 만드는 파라미터
• $\hat W = argmaxP(X|W)$
  --> 이때 W는 확률 분포를 나타내는 파라미터이며, 최대 우도 확률을 만드는 W를 찾음
• 매우 간단한 파라미터 추정법이지만, 데이터에 따라 값이 민감하게 변화함

최대 사후 확률 (Maximum A Posterior, MAP)

• 데이터에 의존적인 MLE의 단점을 해결하기 위해 사용되는 방법론
• 주어진 데이터에 대해 최대 확률을 가지는 파라미터를 찾는 방법
• $\hat W = argmaxP(W|X)$
• 하지만, 사후 확률은 곧바로 계산이 불가능
• 베이즈 정리를 이용해서 사전 확률과 우도 확률의 곱으로 표현 --> $P(X|W)P(W)$
• 추정의 정확도는 사전 확률의 정확도에 좌우됨 --> 얼마나 사전확률을 잘 정의하느냐에 따라서 정확도 달라짐

베르누이 분포(Bernoulli)

• 베르누이 시행이란 두 가지 결과값만을 가지는 실험을 지칭
• 베르누이 시행에 따라 0(실패) 또는 1(성공)의 값을 대응시키는 확률변수를 베르누이 확률변수라 부름
• 이 확률 변수의 분포를 베르누이 분포라 명명
• $P(Y=y_i) = p^{y_i}(1-P)^{1-y_i}$
• L = $\Pi_ip^{y_i}(1-P)^{1-y_i}$

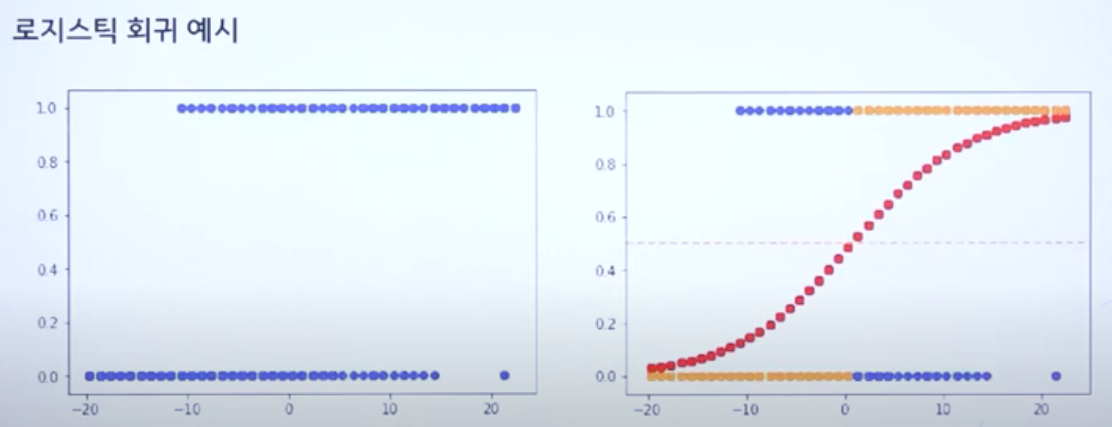
로지스틱 회귀(logistic regression)

• 로지스틱 회귀 모델은 로지스틱 함수 형태의 회귀 모델임
• $P(\hat y = 1|X) = \frac{1}{1+e^{W^TX}} = \sigma(W^TX)$
• 파라미터 p 값이 $\sigma(W^TX)$인 베르누이 분포로 해석 가능

로지스틱 회귀의 likelihood

• L = $\Pi_i\sigma(W^TX_i)^{Y_i}(1-\sigma(W^TX_i))^{1-y_i}$ 베르누이 분포에서 p대신 hypothesis($\sigma(W^TX_i)$)로 변경
• 로그 함수는 단조 증가 함수이므로 L 또는 lnL를 최대로 만드는 W는 동일함
• $lnL = \sum_iy_iln(\sigma(W^TX_i)) + \sum_i(1-y_i)ln((1-\sigma(W^TX_i))$
• 로그 우도 함수를 최대화 --> -로그 우도 함수를 최소화
  --> 그동안 Loss 함수에 사용하기 위한 MLE 설명

SGD for MLE

• 손실 함수로 -lnL를 사용
• $\frac{\partial lnL}{\partial W}$ = 0이 되는 W 값 찾기
• $W_{t+1} = W_t -lr*{\frac{\partial lnL}{\partial W}}$
  

비선형 로지스틱 회귀

• $P(\hat y = 1|X) = \frac{1}{1+e^-W^TX} = \sigma(W^TX)$
• 위의 선형 로지스틱 회귀에서 $w^TX$를 비선형 회귀 함수로 변형하면 됨
• $P(\hat y = 1|X) = \frac{1}{1+e^-W^TX} = \sigma(W_0+W_1X+W_2X^2+W_3X^3 ...)$

Evaluation Metrics

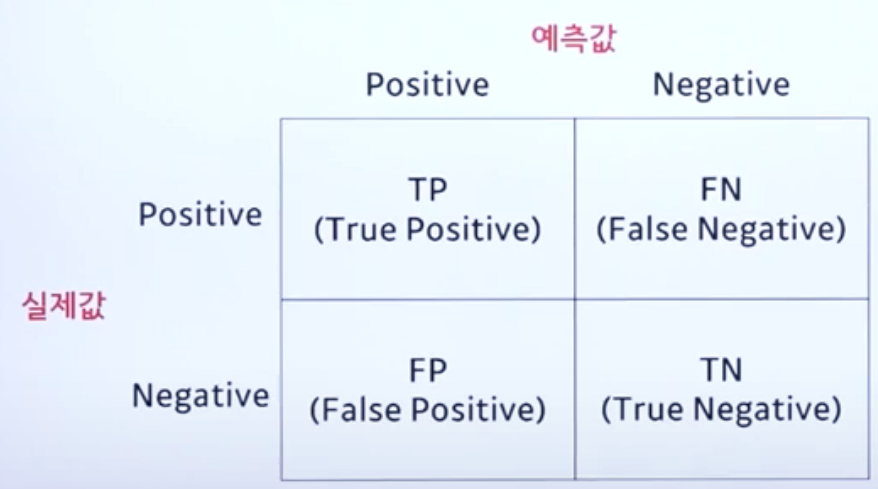
오차행렬(confusion matrix)

• 성능 측정을 위해 예측값과 실제값을 비교한 표
  

• Accuracy(정확도)

  • n개의 데이터샘플 중 예측에 성공한 샘플의 비율 ($\frac{TP+TN}{TP+FN+FP+TN}$)

• Precision(정밀도)

  • 모델이 Positive로 예측한 것 중에 실제값 또한 Positive인 비율 ($\frac{TP}{TP+FP}$)

• recall(재현도)

  • 실제값이 Positive인 것 중 모델이 Positive로 예측한 비율($\frac{TP}{TP+FN}$)

• F1 Score

  • 정밀도와 재현도의 조화 평균 (역수의 산술평균의 역수, $\frac{2*Precision*Recall}{Precision+Recall}$)

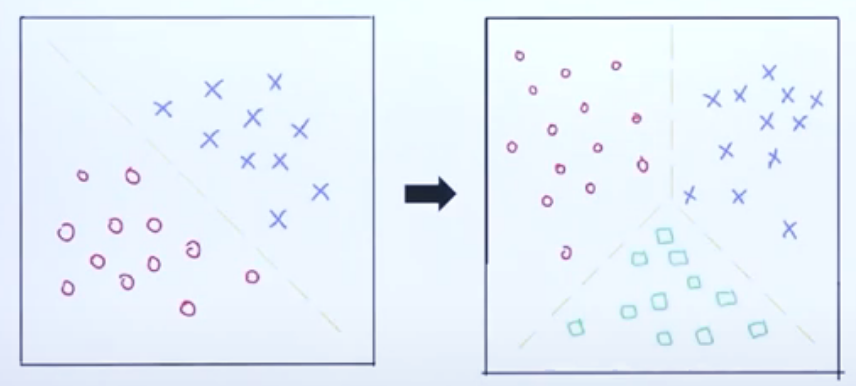
Multiclass Classification

다중 분류 모델(multiclass classifier)

• 분류해야되는 클래스가 여러 개인 상황
• 로지스틱 회귀 모델에 대해 다중 클래스로의 확장이 필요
  

Sigmoid function

• 이진 분류 문제를 위한 비선형 함수
• 함수의 출력값이 항상 0이상 1 이하이며, 중앙 출력값은 0.5임

Softmax function

• 다중 분류 문제를 위한 비선형 함수
  $y_i = \frac{e^{x_i}}{\sum^K_{k=1}e^{x_k}}$(K는 클래스 갯수)

시그모이드 함수와 소프트맥스 함수의 역할

• 입력값을 확률의 성질을 만족하는 결과값으로 변환
  • 1. $0 \leq P(A) \leq 1$
  • 2. P(S) = 1 전체 집단의 확률의 합은 1
  • 3. $P(\phi) = 0$
  • 4. $P(A^c) = 1 - P(A)$

Logistic regression의 Likelihood Function

• L = $\Pi_i\sigma(W^TX_i)^{Y_i}(1-\sigma(W^TX_i))^{1-y_i}$
• 이를 L = $\Pi_iP(y_i = C|X_i)$로 해석 가능
• $y_i$의 값이 0, 혹은 1의 상황에서 0~C의 상황으로 확장 필요

Multiclass Classification의 Likelihood Function

• L = $\Pi_iP(y_i = C|X_i)$ = $\Pi_isoftmax(w^TX_i)=>{y_i}$
• $L_{CE} = -\sum^n_iy_iln(softmax(W^TX_i))$, where $y_i$ = [0,0,1,...,0] ($y_i$는 one hot encoding 된 상태)