Dimension Reduction

• 데이터에 대한 차원 축소는 속도뿐만 아니라 성능 면에서 필요
• 모델 학습에 불필요한 피처(속도 향상)나 방해되는 피처(성능 향상)를 제거해야함
• 방해되는 피처란, over-fitting 문제를 발생시키는 피처로 이해 가능
• 이는 차원의 저주와 관련 있는 현상임

Curse of Dimensionality(차원의 저주)

• 차원이 증가하면서, 학습 데이터 수(N)가 차원의 수(p)보다 적어져 성능이 저하되는 현상
• 차원 내에 존재하는 데이터들이 희박해지는 (sparse) 현상
  
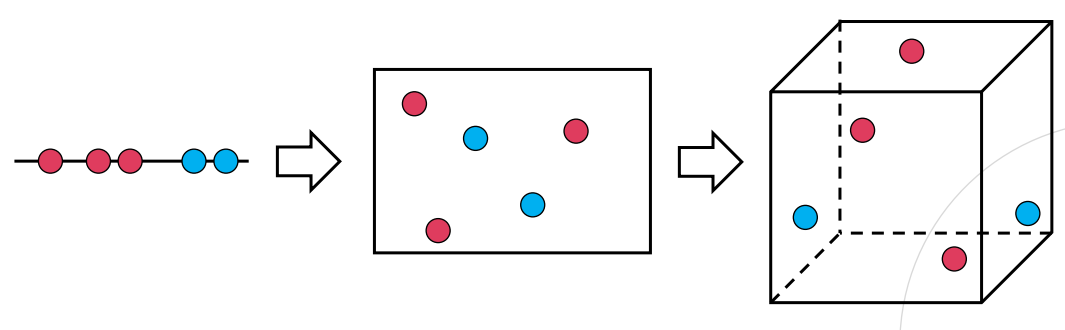
• 빈 공간이 많아지며, 이는 정보가 없는 공간이 많아지는 것을 의미
• 해결할 수 있는 방법은 크게 두 가지가 있음
  1. 데이터를 수집
  2. 차원을 축소시킴
• 차원 축소 방법으로는 크게 feature selection과 feature extraction 두 가지 사용 --> 데이터 전처리

Feature selection(형상 선택)

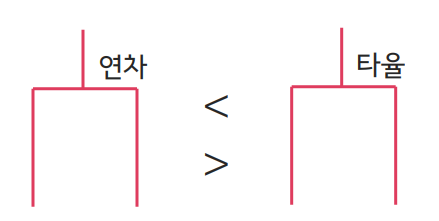
• 종속 변수(라벨)와 가장 관련성이 높은 피처만을 선택해, 나머지를 제외시킴
  (ex. 각각의 피처를 모델에 포함시킴으로써 손실값이 낮아지는 정도를 비교)
• Bagged tree에서의 피처 중요도 계산
  
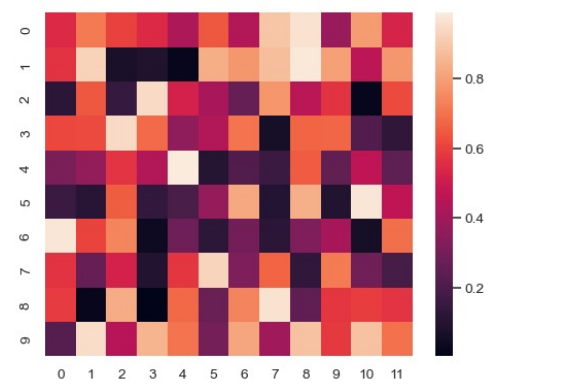
• 피처 사이의 상관 관계가 매우 높아서, 한 쪽이 의미 없는 경우 제외시킴
• 일반적으로 히트맵(heatmap)을 통해 여러 피처의 공분산(covariance) 분석
  

Feature Extraction(형상 추출)

• 개별 피처를 제거하는 대신, 저차원 공간으로 투영시켜 데이터와 모델을 단순화시킴
• 다음과 같은 알고리즘들이 있음
  1. 주성분 분석(PCA)
  2. 특이값 분해(SVD)
  3. LDA
  4. t-SNE
  5. UMAP

PCA(주성분 분석)

PCA

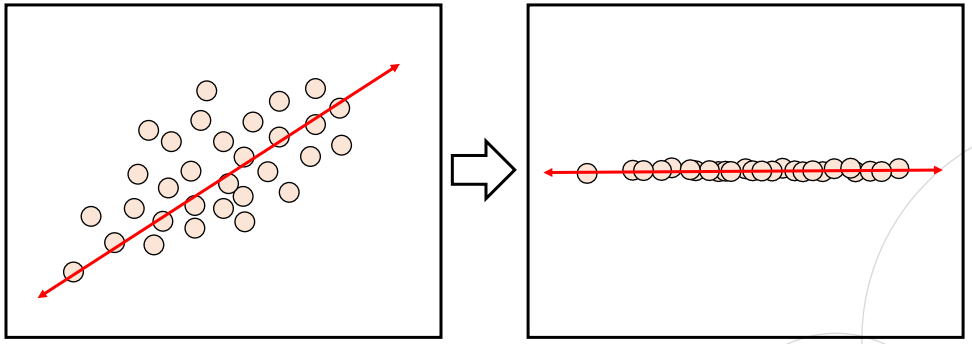
• 전체 데이터의 분포를 가장 잘 설명할 수 있는 주성분을 찾아주는 방법론
• 주 성분이란 그 방향으로 데이터들의 분산이 가장 큰 방향 벡터를 의미함
• 분산이 가장 크다는 말은 데이터가 가장 넓게 퍼져있어 구분짓기 쉽다는 뜻임
• 주성분 방향 벡터를 찾아 데이터를 그 위로 투영(projection)시켜 차원을 한 단계 낮춤
  

공분산(covariance)

• 두 변수 x,y의 공분산은 다음과 같이 정의됨
  $cov(x,y) - E[(x-\bar x)(y-\bar y)] = E[xy]-\bar{xy}$
• 한쪽 변수의 값이 커짐에 따라 다른 변수 또한 커지면 양의 상관관계를, 작아지면 음의 상관관계를 갖음
• 서로 상관관계가 없는 독립적인 관계에서는 공분산이 0이 됨

공분산 행렬(covariance matrix)

• 각각의 데이터 피처들 사이의 공분산 값을 원소로 하는 행렬
• $x = [x_1,x_2,...,x_N]$
• $C = E[(x- \bar x)(x-\bar x)^T]$ : N X N 행렬
  $C_{ij} = E[(x_i- \bar x)(x_j-\bar x)^T]$
• 열에 대한 부분이 피ㅣ처가 되며, 피처 사이의 공분산이 원소가 됨
• 공분산 행렬은 symmetric 성질을 만족함

고유값과 고유벡터 (eigenvalue & eigenvector)

• 행렬 A를 선형변환으로 봤을 때, 선형 변환 A 이후에도 자기 자신의 상수배가 되는 벡터를 고유벡터(eigenvector) = $v$라 부르고 이 때의 상수배 값을 고유값(eigenvalue) = $\lambda$라 함
• $Av = \lambda v$
• 즉, 선형변환 A에 의해 방향은 보존되고 스케일만 변환되는 방향 벡터와 스케일 값을 의미
  

고유값 분해(eigen decompotion)

• 행렬 A를 고유벡터를 열벡터로 하는 행렬과 고유값을 대각원소로 하는 행렬의 곱으로 분해
• 고유값과 고유벡터는 정방행렬(nxn)에 대해서만 정의됨
• 단, 행렬 A가 n개의 일차독립인 고유벡터를 가져야 함
  (일차독립: 어느 한 벡터도 다른 벡터들의 일차결합으로 표현 불가능)
• 대칭행렬(symmetric matrix)은 항상 고유값 분해 가능
  
  
  
  
  
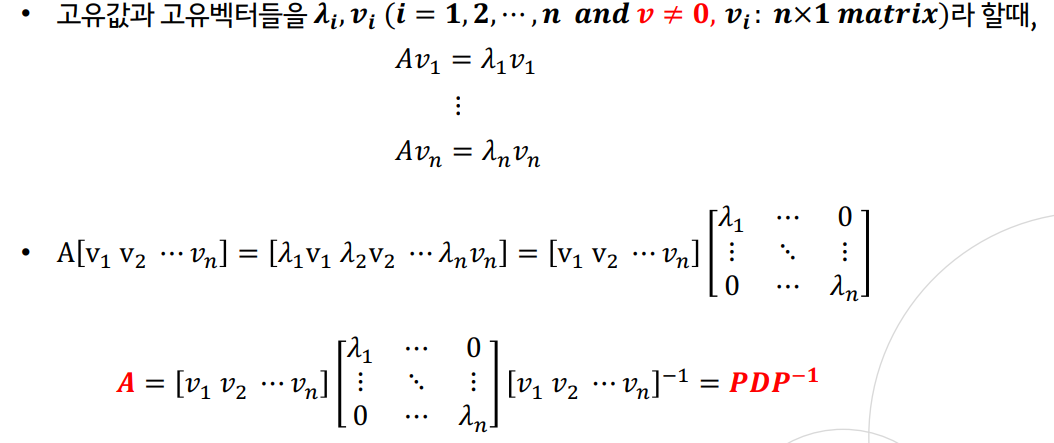
• 전체 데이터의 분포를 가장 잘 설명할 수 있는 주성분(방향벡터)을 찾아주는 방법론
• 이를 데이터의 공분산 행렬에 대한 고유값 분해를 통해 얻음
• 공분산 행렬은 대칭 행렬이기 때문에 고유값 분해가 항상 가능함
• 가장 큰 분산을 가진 방향의 고유벡터로 데이터를 투영시켜 차원을 축소시킴
  --> 고유값 $\lambda$를 찾고 그에 해당하는 $v_i$를 찾아 데이터 차원을 축소