[논문 리뷰] Understanding Contrastive Representation Learning through Alignment and Uniformity on the Hypersphere
논문
Introduction
- Representation을 학습하는데 있어 norm을 통해 feature의 영역을 unit hypershpere으로 제한하는 것은 학습 안정성을 높이고 클래스를 적절히 분류하여 선형 분리가 가능하도록 만든다.
- norm은 보편적인 방법이지만 encoder에 따라 representation은 다양하며 최근 연구들은 representation이 불필요한 디테일에 불변하며, 최대한 많은 정보를 보존해야함을 주장한다.
- 따라서, representation은 alignment와 uniformity라는 두 가지 속성을 만족시켜야 한다.
alignment: 유사한 sample은 유사한 feature을 가진다.
uniformity: feature의 분포는 정보를 최대한 보존한다 = unit hypershpere에서의 균일 분포 - 본 논문에서는 contrastive learning(https://89douner.tistory.com/334)이 negative sample이 무한하다는 조건 하에 위 두 속성을 최적화함을 보인다.
- 또한, 이 두 속성을 측정하는 지표가 downstream task의 성능과 연관이 있음을 보인다.
(downstream task란 self-supervised learning으로 학습된 feature들이 얼마나 잘 학습되었는지 판단하기 위해 사용되는 task)
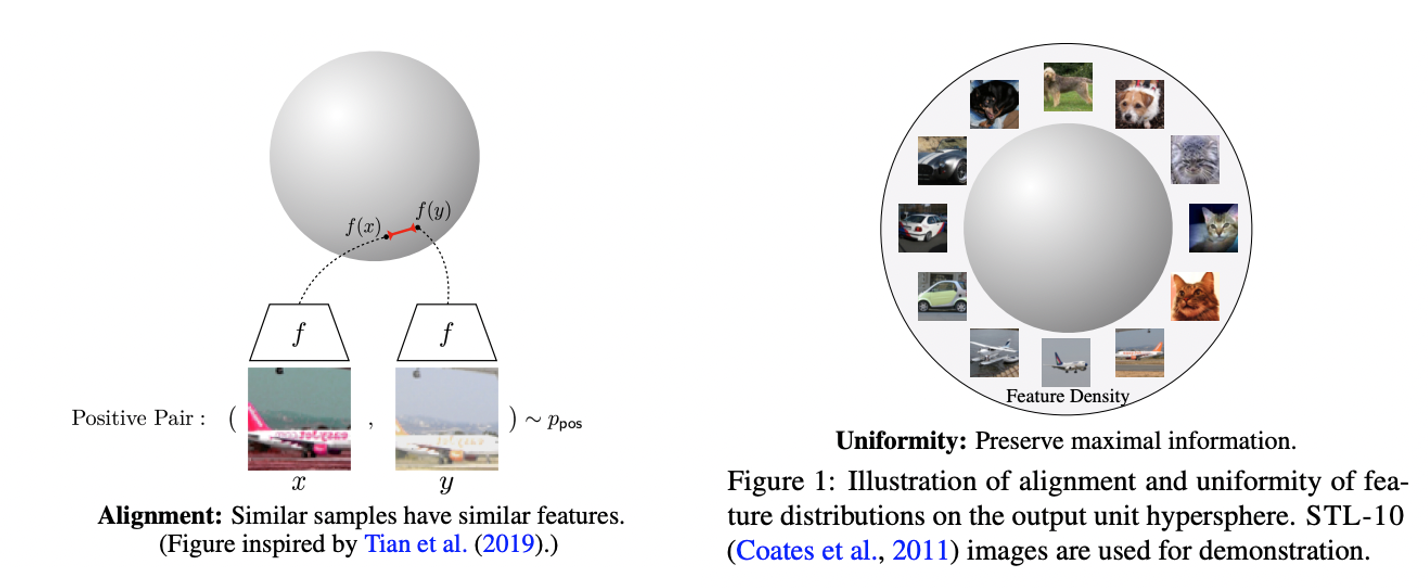
Contrastive Representation Learning

출처: https://ai.googleblog.com/2020/04/advancing-self-supervised-and-semi.html
- Contrastive representation learning이란 unlabeled data로부터 representation을 학습하는 방법으로 augmentation을 통해 positive pair sample을 만든다.
- 동일한 샘플로부터 나온 이미지끼리는 positive이므로 근처에 위치하도록 다른 샘플로부터 이미지와는 negative이므로 멀어지도록 학습한다.
- Sample data의 분포와 augmentation된 positive pair data의 분포를 각각 , 라 할 때 Symmetry와 Matching marginal을 가정하며 그 의미는 아래 식과 같다.
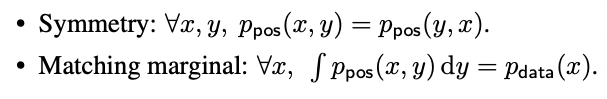
Contrastive loss
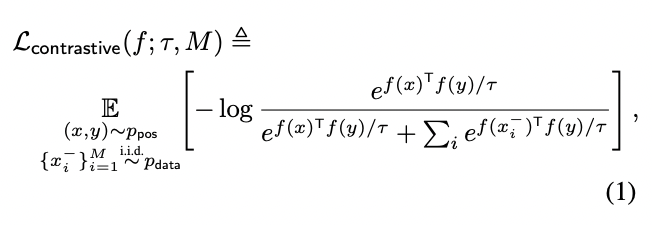
: 같은 이미지에서 얻은 augmentation 이미지 간의 유사도(similarity)
: 다른 이미지에서 얻은 augmentation 이미지 간의 유사도(similarity)
: negetive sample의 수
(scalar temperature hyperparameter): 일반적으로 overconfident한 딥러닝의 결과값을 더욱 실제 confidence에 가깝도록 만들도록 하는 calibration의 한 기법
Constrastive loss: https://nlog-blog.tistory.com/entry/Contrastive-Learning-1-Vision
Calibration: https://3months.tistory.com/490
Feature Distribution on the Hypersphere
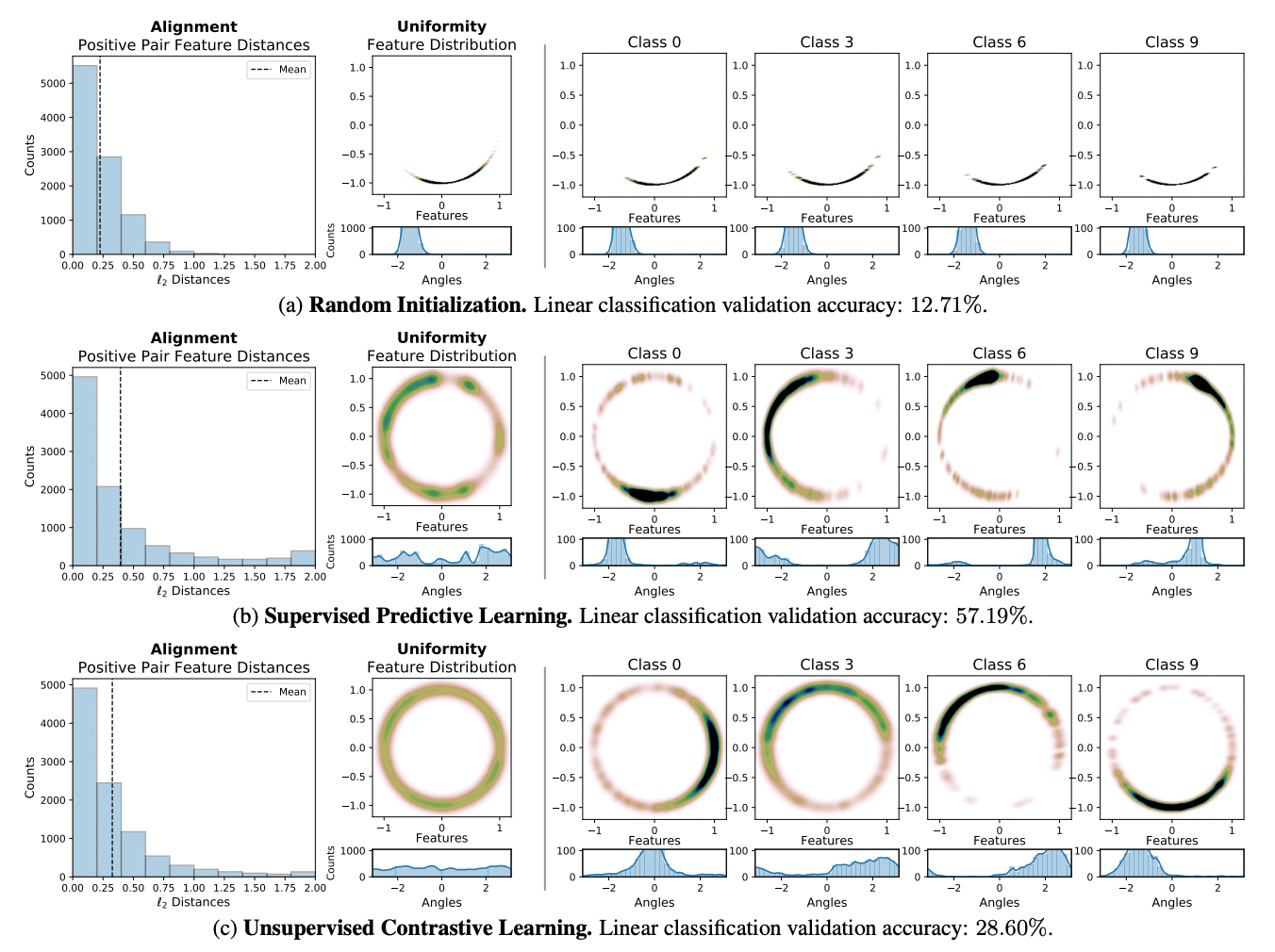
Constrastive loss는 positive pairs 간의 features는 끌어당기고 negative pairs 간의 features는 밀어내도록 만든다. 이 loss가 alignment와 uniformity을 만족시키도록 작동함을 증명하기 위해 본 연구에서는 CIFAR-10 representation을 다음 세 가지 방법을 통해 시각화 하였다.
- Random initialization
- Supervised predictive learining
- Unsupervised contrastive learning
Encoder는 전부 AlexNet을 사용하였으며 2차원으로 맵핑한 결과 contrastive learning을 한 feature들이 가장 고르게 분포하였으며, positive pair끼리 가장 가깝게 클러스터링 되었다.
Contrastive loss와의 관계성을 직관적으로 이해하기 위해 앞서 가정했던 Symmetry로부터 아래와 같은 식을 유도할 수 있다. 이 때 식(1)은 항상 양수이고 bounded below이므로 loss는 식(2)를 작게 만들도록 한다. 즉, positive pair features가 aligned 된다.

위 식에서 encoder가 완벽하게 aligned되어 이라고 가정하면 loss를 최소로 하는 최적화 과정은 negative pair의 유사도가 작아지도록 학습한다. 이 과정에서 모든 feature들을 서로 밀어내기 때문에 균일한 분포를 만든다.
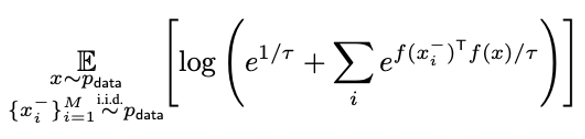
Quantifying Alignment and Uniformity
Alignment loss
Alignment loss는 positive pairs 간의 거리의 기댓값으로 정의한다.
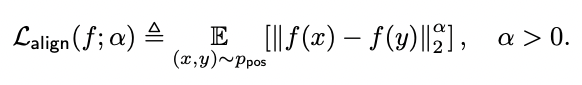
Uniformity loss
균일분포로 수렴하고 한정된 points에 대해서도 적용 가능한 Gaussian potential kernel을 이용한다. Uniformity loss는 평균 pairwise Gaussian potential에 로그를 취한 값으로 정의한다.
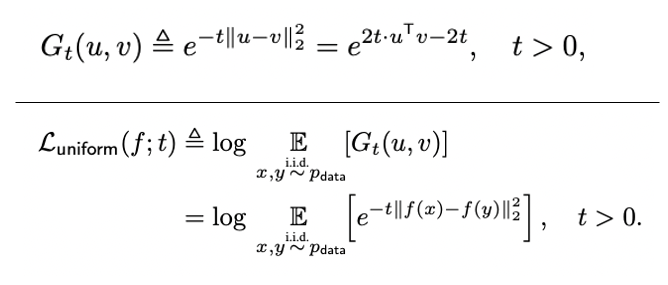
여기서부터 증명 내용들..처음 보는 수학 개념들이 나오는데 이해가 안된다ㅠㅠ
Measure space, Borel set 등에 관한 개념
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=at3650&logNo=220887951885
Limiting Behavior of Contrastive Learning
본 논문에서는 의 를 Borel space 로 맵핑하는 최적의 encoder를 찾기 위해 두 가지 metric을 제시하였다.
Realizability of perfect uniformity
- 에서의 데이터 manifold 차원이 feature space인 보다 작으면 perfect uniformity는 성립할 수 없으며 와 모두 한정된 데이터셋으로부터 augmentation 하여 만든다면 perfectly aligned와 perfectly uniform을 모두 만족시킬 수는 없다.
- Perfectly uniform encoder는 이고 가 bounded density를 가진다는 조건 하에 존재할 수 있다.
- Negative sample이 많을수록 downstream task에서의 성능이 오른다는 결과가 있었으며 본 연구에서도 일 때 contrastive loss의 수렴 과정을 분석하여 asymptotic함을 보인다.
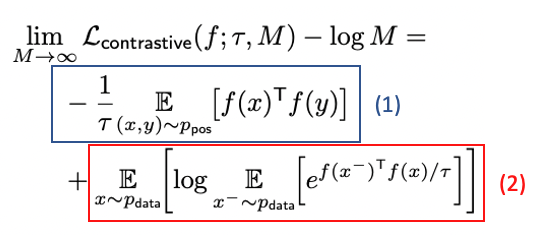
Results
- Perfectly aligned 할 때 식(1)은 최소가 된다.
- Perfectly uniform encoders가 존재한다면, 식(2)이 최소일 때 그것이 된다.
- 위 식의 수렴을 위해 absolute deviation from the limit decays in (???)
Relation with
- 식(2)와 비교할 때 은 log가 기댓값 밖으로 빠져있다.(without changing the minimizer??)
- 하지만, pairwise nature 덕분에 의 형태가 훨씬 단순하며 에서의 softmax 연산을 피할 수 있다.
Relation with feature distribution entropy estimation
- 가 한정된 sample에서 균일할 때 식(2)는 의 entropy estimator로 볼 수 있다.
- 이 때, 는 vMF KDE에 의해 sample들의 분포인 를 따라간다.
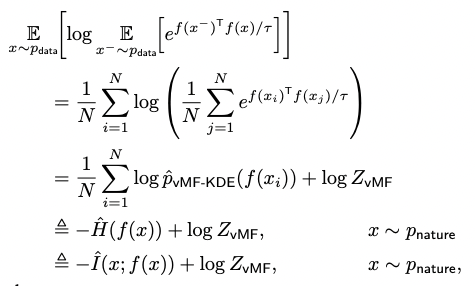
Experiments
가설 검증을 위해 STL-10, NYU-DEPTH-V2, IMAGENET, BOOKCORPUS 데이터셋으로 실험을 하였으며 다음과 같은 결과들을 확인하였다.
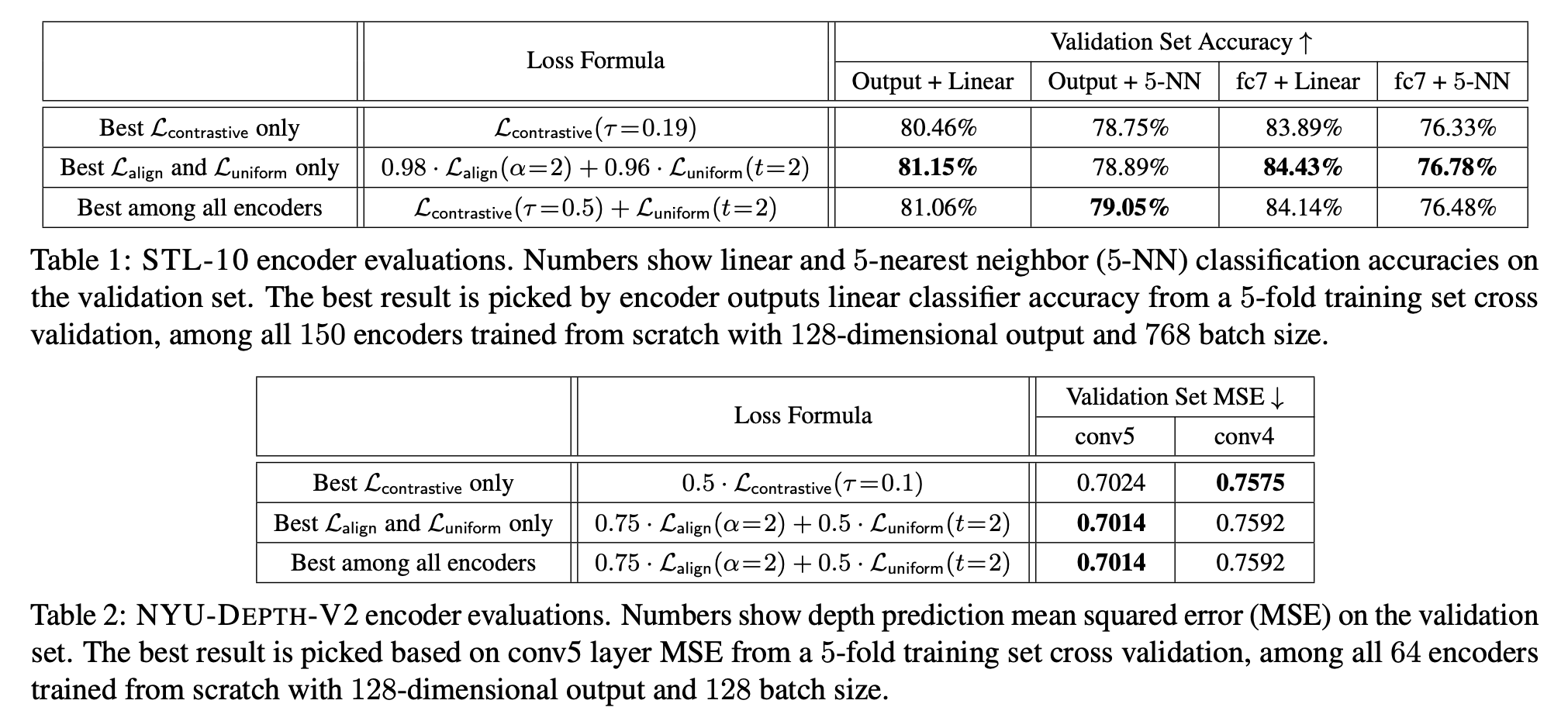
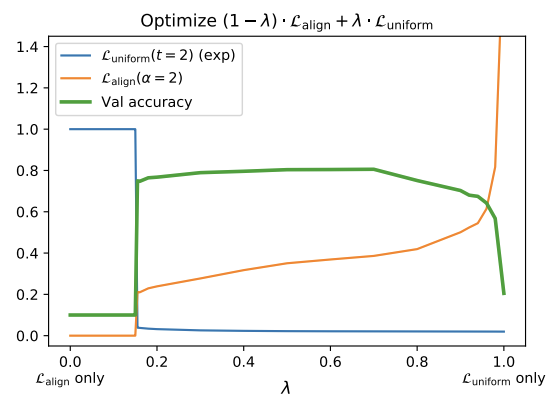
- 과 은 downstream task 성능 향상에 연관이 있다.
- 과 중 한가지의 loss만 사용하더라도 보다 좋은 성능을 보인다. 가 점근적으로 uniformity와 alignment를 최적화하는 것을 앞서 증명하였기에 한정된 sample들로 두 속성을 바로 최적화시키는 것은 합리적이다.
- 좋은 representation을 얻는데 있어 uniformity와 alignment는 모두 중요한 요소이다. 하지만, 둘의 가중치의 비율이 너무 크지만 않다면 문제 없이 좋은 representation을 얻을 수 있다.
