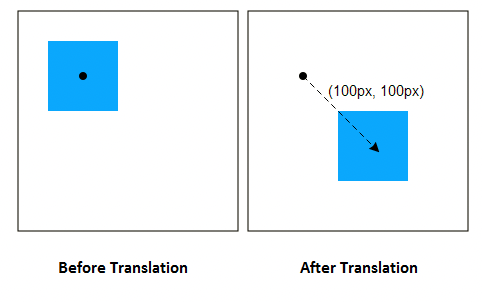
Transformation

Notation

• 주어진 영상에 특정 알고리즘을 적용하여 변환된 이미지를 얻어내는 것.

DoF란?

• 자유도(Degree of Freedom)로 물체의 위치와 상태를 나타내기 위해 필요한 변수의 개수를 의미한다.

Rigid Transformation(강체 변환)

• Euclidean transformation이라고도 하며 형태와 크기를 유지한 채 위치와 방향만 바뀔 수 있는 변환을 의미한다.
• Rotation & Translation are not commutative
  -> 회전 후 평행이동하는 것과 평행이동 후 회전하는 것은 다르다

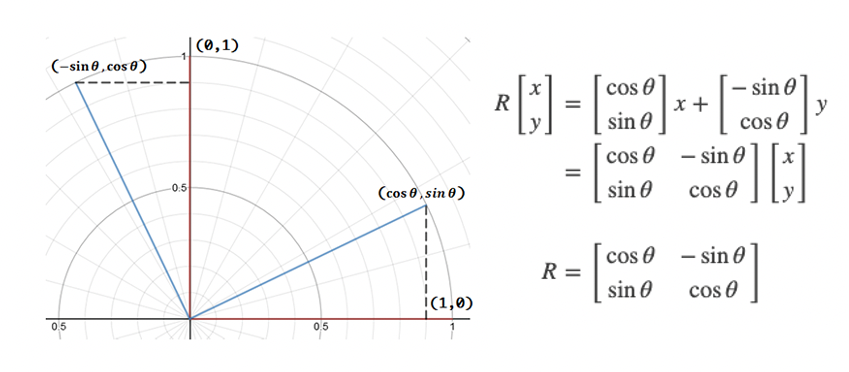
Rotation

• $(x,y)$를 반시계 방향으로 $\theta$ 라디안(radian)만큼 회전시키는 변환
• 변수가 $\theta$뿐이므로 DoF는 1이 된다.
  
• 회전 행렬은 $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$과 $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$의 기저벡터로 이루어진 좌표계를 $\begin{bmatrix} cos\theta \\ sin\theta \end{bmatrix}$과 $\begin{bmatrix} -sin\theta \\ cos\theta \end{bmatrix}$의 기저벡터로 이루어진 좌표계로 바꿔준다.
  

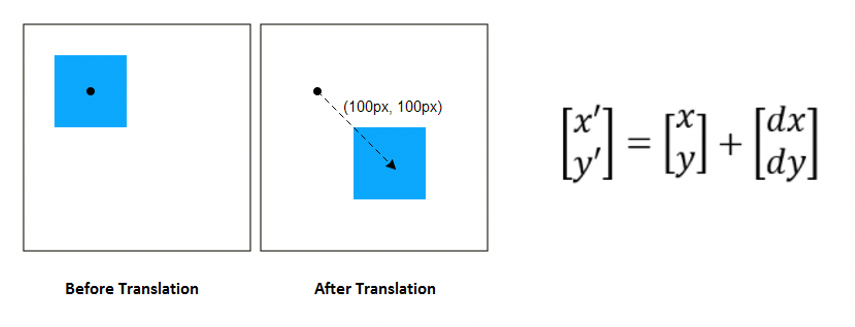
Translation

• $(x,y)$를 $dx, dy$만큼 평행이동
• $dx, dy$를 변수로 가지므로 DoF가 2이다.
  

Similarity transformation(닮음 변환)

• Rigid transform에 스케일 변화까지 허용되는 변환
• Rotation, Translation, Scale change의 변수들로 구성되므로 DoF는 4이다.
• 3D에서는 Rotation과 Translation의 DoF가 각각 3이 되어 7의 자유도를 가지게 된다.(3D에서는 회전은 x,y,z축을 기준으로 하여 3가지의 $\theta$가 필요하기 때문)
  

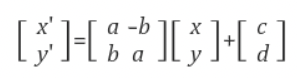
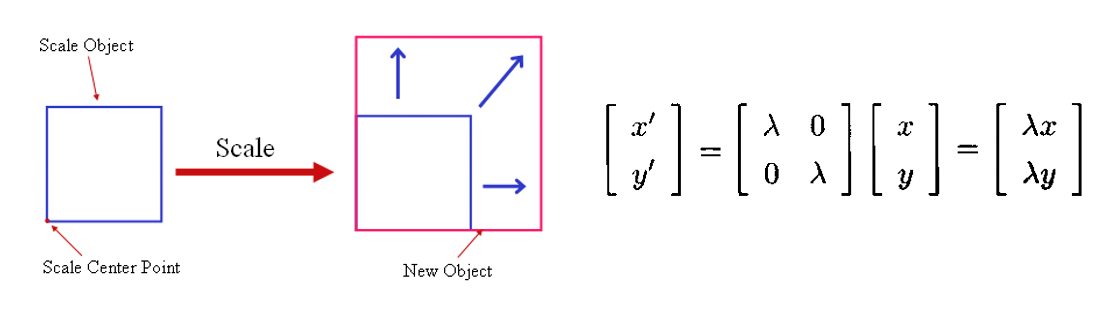
Scale change

• $\lambda$를 변수로 가지므로 DoF가 1이다.
  

Affine transformation

• Similarity transform에 shearing, 반전(reflection)까지 허용되는 변환
• 직선, 길이(거리)의 비, 평행성을 보존한다.
• 자유도는 6이다.
  

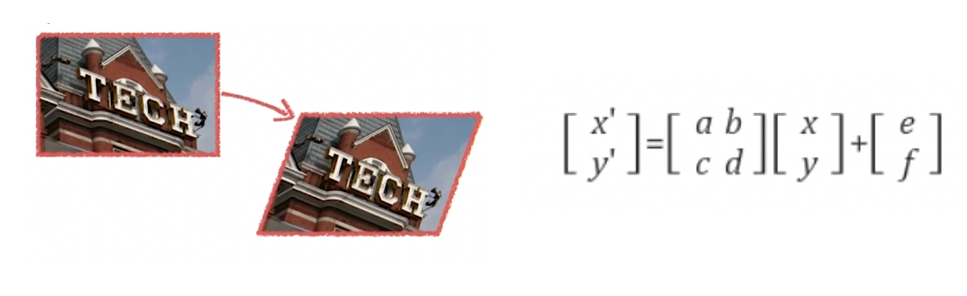
Projective=Homography transformation(원근변환)

• 3D공간에서 2D 공간으로 투영하거나, 서로 다른 두 평면 간의 매핑 관계를 모델링하기 위한 변환
• 자유도는 8이다. 9가 아닌 이유는 $(x,y,1), (wx',wy',w)$이 homogeneous 좌표이므로 scale을 결정할 수 없기 때문
  

Homogeneous coordinate란

• n차원의 사영공간을 n_1개의 좌표로 나타내는 좌표계
• $(1w,2w,3w,w) = (1,2,3,1) = (2,4,6,1)$는 전부 3차원의 $(1,2,3)$좌표와 동치이다, 따라서 스케일은 무시하게 된다.
• Tranlation은 벡터의 덧셈으로 표현하므로 하나의 matrix로 표현할 수가 없다. 예를 들어, affine transformation은 $X' = MX+T$로 표현된다.
• 하지만 Homogeneous 좌표를 사용하면 아래와 같이 하나의 matrix로 표현할 수 있다.
  
• 따라서, w가 0일 때는 translate를 하지 않으며 1일 때는 translate를 하게 된다.

Linear transformation(선형변환)

• 벡터의 위치는 변하지 않고 방향과 크기만 변하는 변환
• 함수 f에 대해 $f(au+v) = af(u)+f(v)$라는 선형성을 만족
• Rotation, Scale change, shearing 등이 전부 선형변환에 속한다.

Conclusion

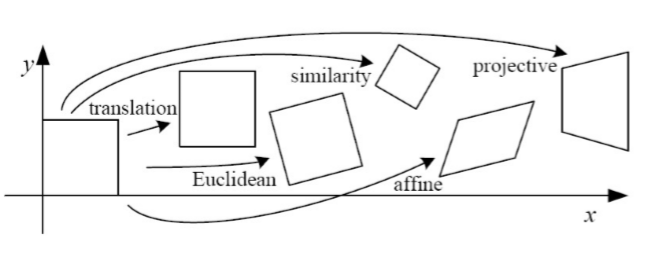
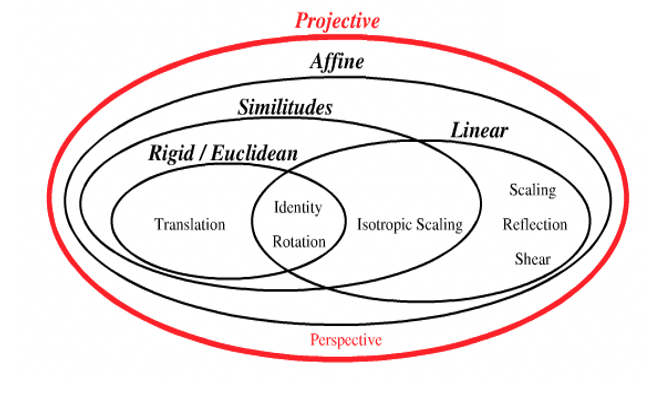
Materials

• Translation & Rotation(2D)
  https://www.youtube.com/watch?v=YXGUGSAv09A&t=444s
• Rt in euclidian
  https://www.youtube.com/watch?v=YXGUGSAv09A&t=888s

Reference

• https://adioshun.gitbooks.io/geometry/content/2d-transformation.html
• https://darkpgmr.tistory.com/79
• https://coding-groot.tistory.com/89
• https://o-tantk.github.io/posts/derive-rotation-matrix/#:~:text=%EB%A8%BC%EC%A0%80%20%EA%B8%B0%EC%A0%80%20%EB%B2%A1%ED%84%B0%EC%9D%B8%20(1,%2Ccos%CE%B8)%EC%9D%B4%20%EB%90%9C%EB%8B%A4.