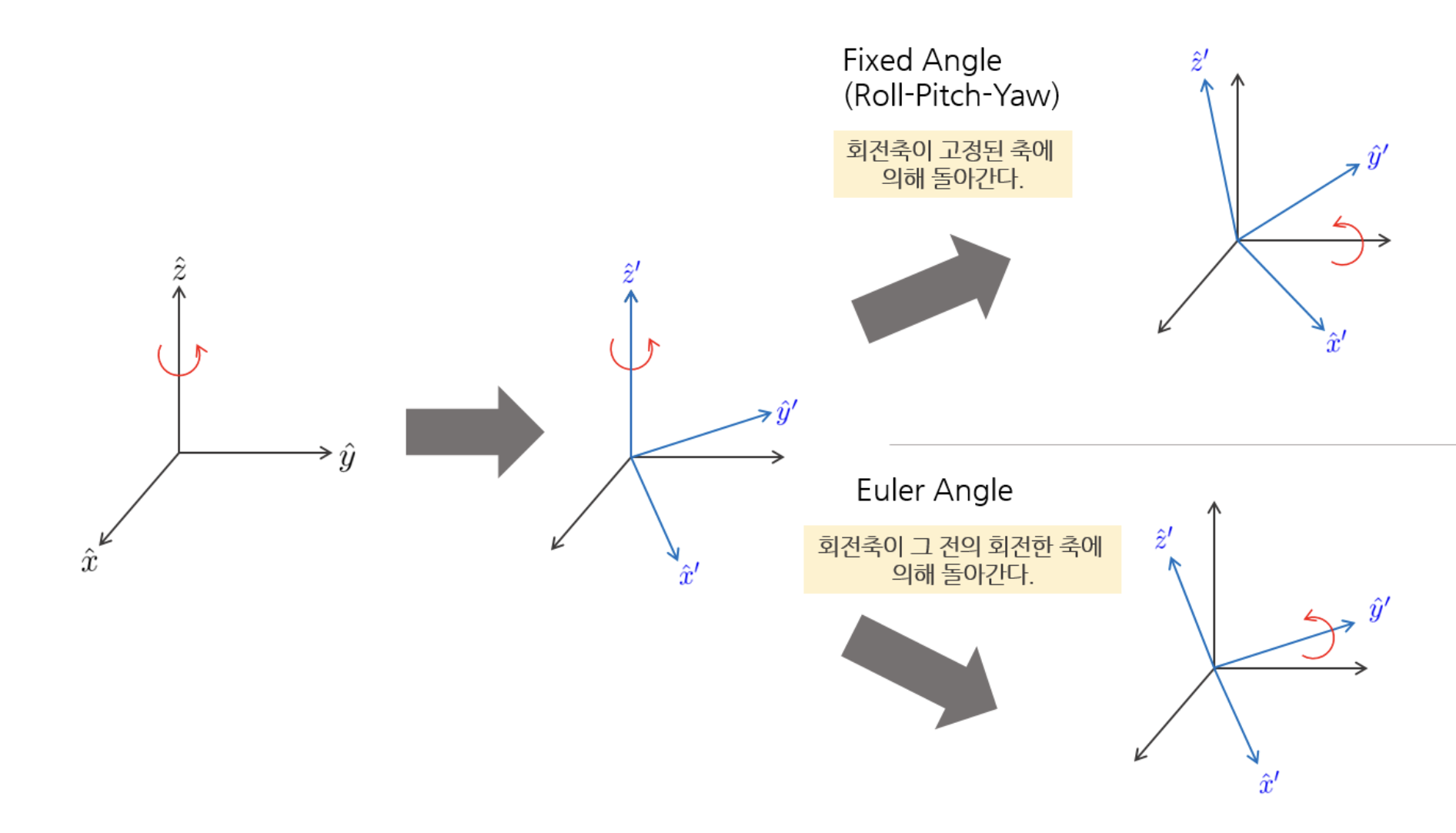
Euler Angle

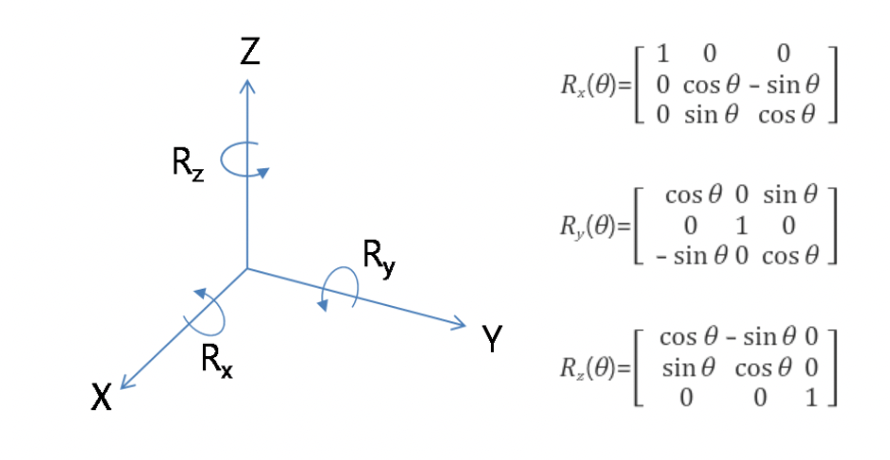
Rotation matrix(3D)

• 3D에서의 회전은 각 축을 기준으로 $\theta$만큼 회전할 때의 회전행렬로 나타낼 수 있다.
• $x,y,z$축에서의 회전 각을 각각 $\gamma, \beta, \alpha$라고 할 때 3D 회전은 회전변환을 조합하여 다음과 같이 표현할 수 있다.
  $R=R_z(\gamma)R_y(\beta)R_x(\alpha)$
  

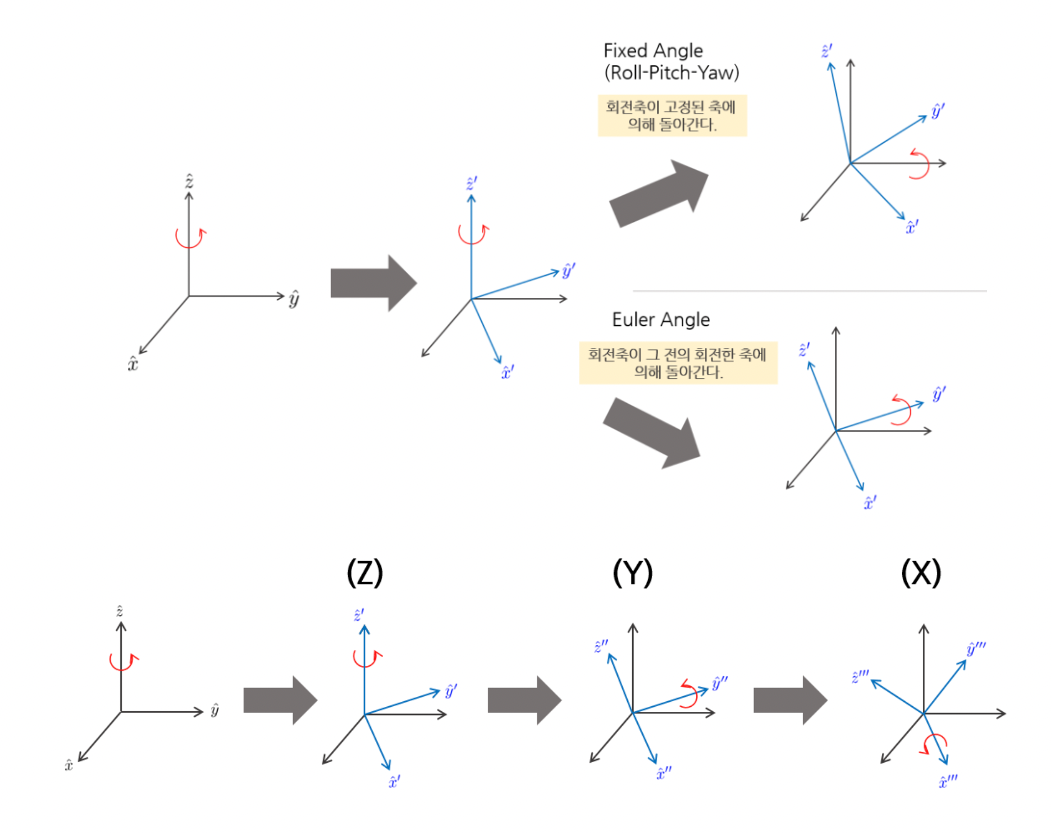
Euler Angle vs Fixed Angle

• 오일러 각도란 회전한 축을 기준으로 다음 회전을 하는 것을 의미한다.
• $x,y,z$축에서의 오일러 각을 각각 $\gamma, \beta, \alpha$라고 할 때 $x$축으로 $\gamma$만큼 회전한 후, 회전한 축 $(x',y',z')$의 $y'$축을 기준으로 $\beta$만큼 회전한다. 이후, 새로운 회전축 $(x'',y'',z'')$의 $z''$축을 기준으로 $\alpha$만큼 회전한다.
  

Gimbal lock

https://homoefficio.github.io/2015/07/17/Gimbal-Lock/

• 오일러 각도로 물체를 표현할 때 같은 방향으로 두 회전 축이 겹치는 현상으로 3개의 자유도 중 1개의 자유도를 잃어버리게 된다.
• $y$축을 90도 회전시켰을 때 gimbal lock이 발생하여 $\beta$가 제한된다.
  
• $\beta=\pm90$일 때 $cos\beta=0$이 되어 $\gamma$와 $\alpha$를 구할 수 없는 singular matrix를 가지게 된다.

Discontinuity

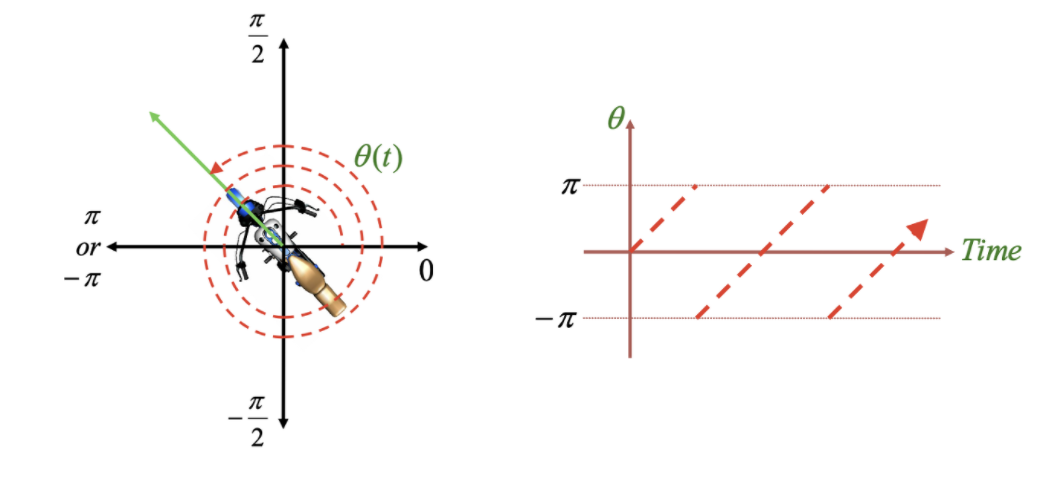
• many-to-one correspondences라고도 부르며 모션은 연속적이지만 이를 표현하는 방식이 비연속적인 것을 의미한다.
• 각도가 $-\pi$~$\pi$로 제한되어 있어 나타나는 현상으로 30도와 390가 똑같이 표현된다.

Materials

• Euler angle
  https://www.youtube.com/watch?v=YXGUGSAv09A&t=2173s
• Gimbal lock
  https://www.youtube.com/watch?v=zc8b2Jo7mno&t=40s

Reference

• https://darkpgmr.tistory.com/81
• https://gofo-coding.tistory.com/entry/Orientation-Rotation
• https://edward0im.github.io/engineering/2019/11/12/euler-angle/