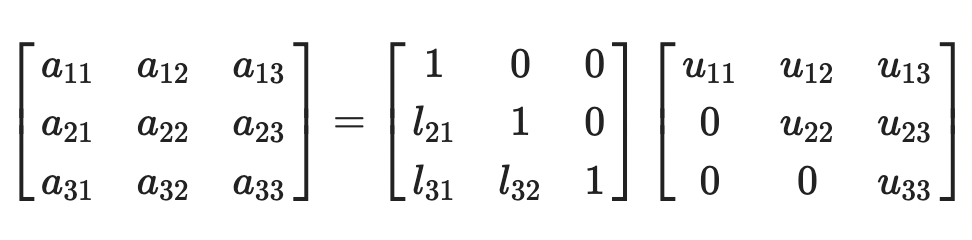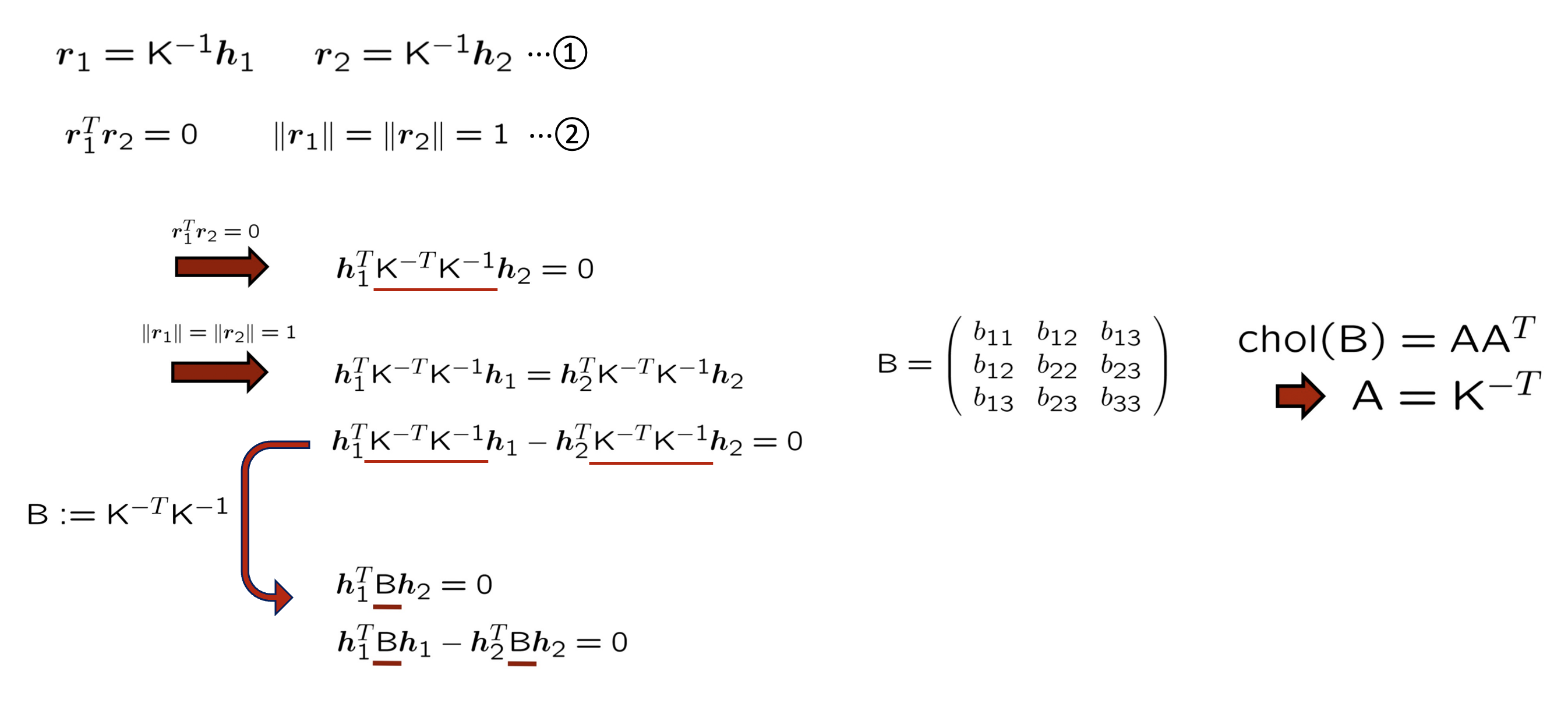Cholesky decomposition

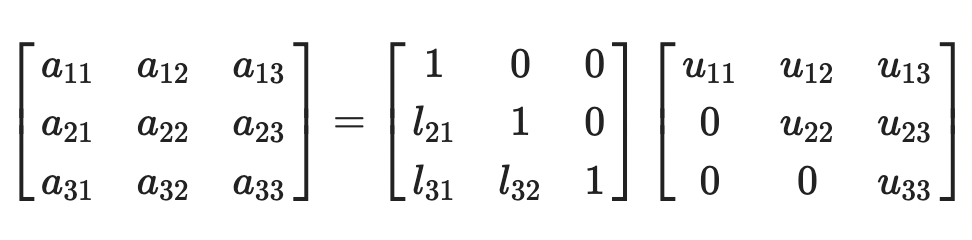
• LU분해는 위 그림과 같이 lower trianguler matrix와 upper triangular matrix로 분해하는 것을 의마한다.
• $A=LU$에서 $A$가 symmetric matrix라면 $A=A^T$이므로 $A=LL^T=L^TL$과 같은 형태로 분해하여 LU분해와 같은 형태를 만드는 것을 생각해볼 수 있다.
• 단, 이 때 $A$는 semi-positive definite 행렬이어야 한다.

  • 행렬 $L$과 임의의 벡터 $x$의 곱 $Lx$의 L2-norm은 항상 0 이상의 값을 가진다.
  • $|Lx|^2 = (Lx)^T(Lx)=x^TL^TLx$로 표현할 수 있고 $L^TL$을 행렬 $A$라고 하면 $x^TAx \ge0$이 된다.
  • 위와 같은 성질을 만족할 때 semi positive definite 행렬이라 하므로 $A$의 조건이 된다.

Calibration

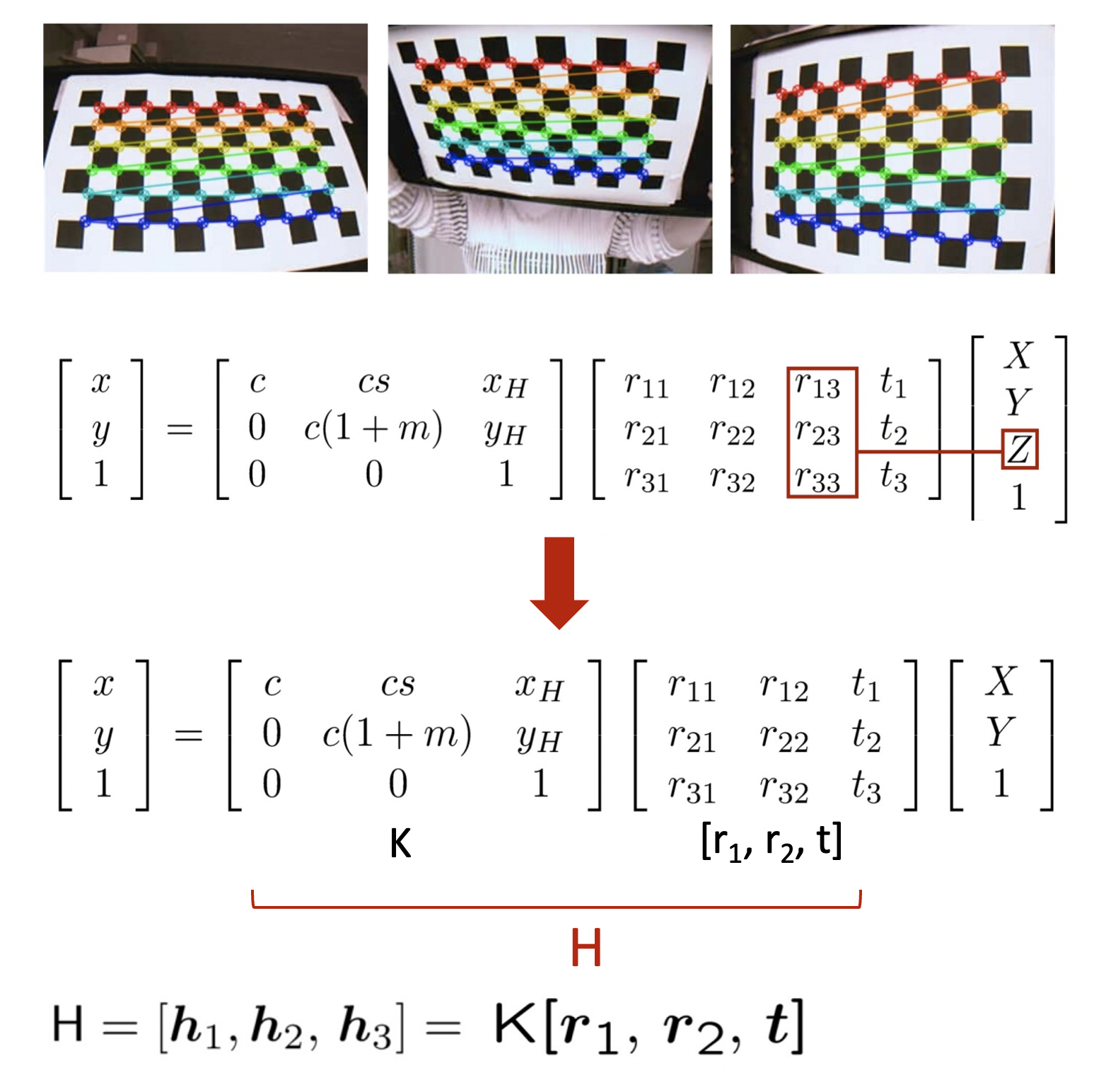
• World coordinate system을 xy plane의 체크보드의 코너로 설정하여 $Z=0$이 된다.
• 따라서, Z축에 대한 rotation parameters와 Z는 제거할 수 있으며 이 경우 완전한 rotation matrix가 아니므로 QR분해를 통해 DLT를 할 수 없다.
• Homography $H$는 scale을 제외한 8개의 DoF를 가지므로 4개의 쌍의 매칭점이 필요하다.

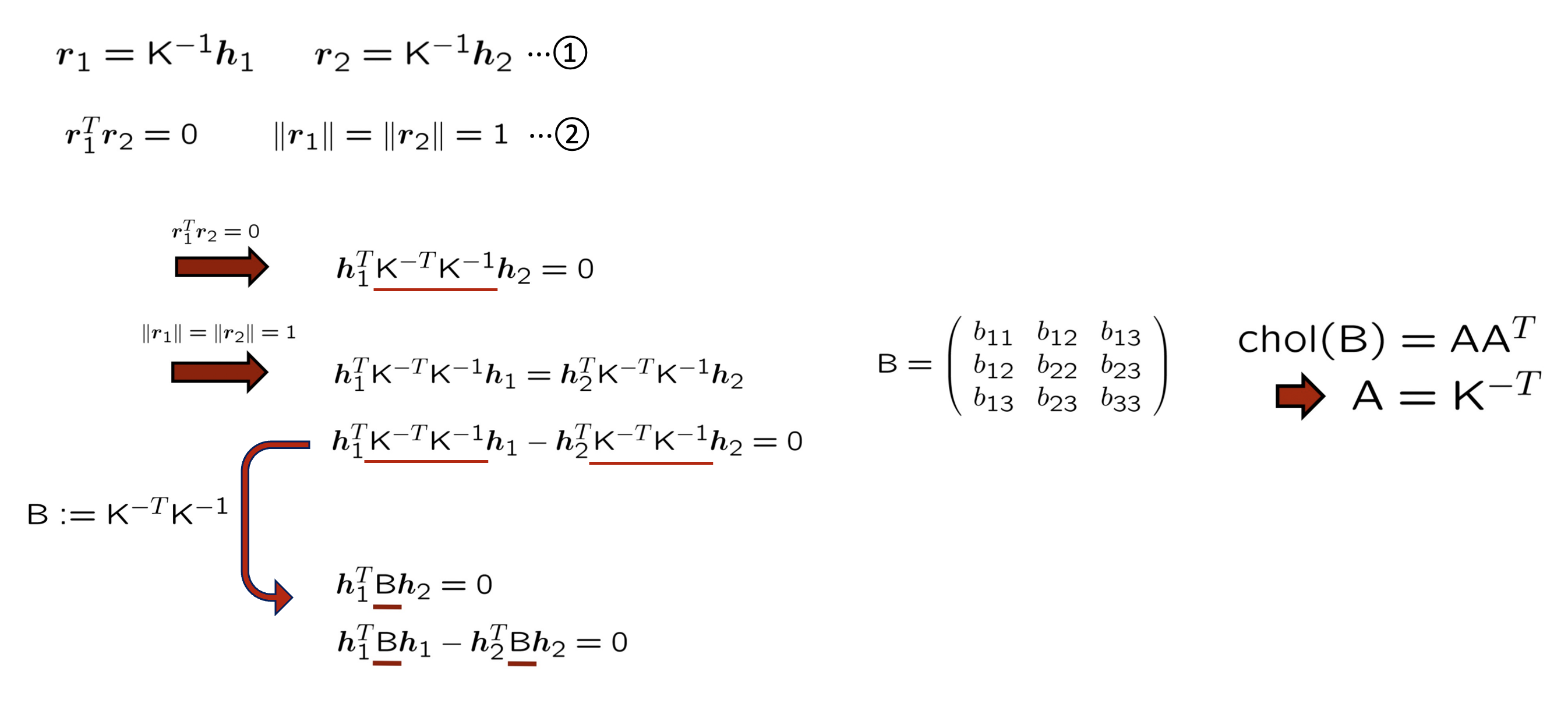
• $[h_1,h_2,h_3]=K[r_1,r_2,t]$로부터 $K^{-1}[r_1,r_2,t]=[h_1,h_2,h_3]$가 되므로 식1을 얻을 수 있으며 $r_1$과 $r_2$가 orthonormal하므로 식2를 얻을 수 있다.
• 위 식들로부터 알고 있기 때문에 계수로 볼 수 있는 $h$와 모르는 파라미터로 이루어진 $K$에 대한 두 개의 방정식을 얻을 수 있으며 $K^{-T}K^{-1}$를 $B$로 치환한다.
• $B$는 symmetric and positive definite matrix이므로 cholesky decomposition이 가능하며 따라서 $B$를 알면 $K$를 계산할 수 있다.

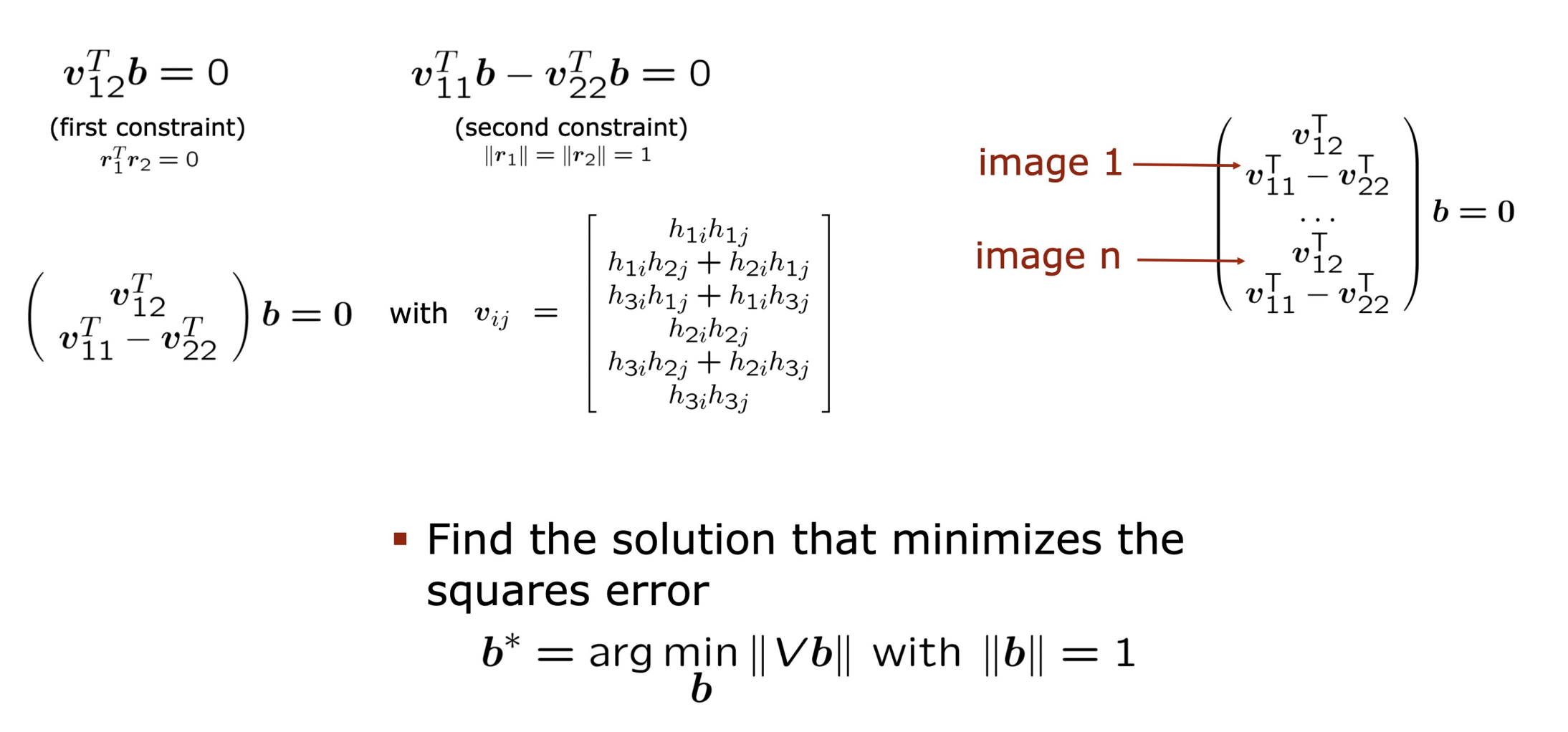
• 위의 두 제약식을 $v$와 $b$에 대한 식으로 정리할 수 있다.
• 이미지가 n개 일 때 $2n \times 6$의 matrix $V$가 나오며 $Vb=0$을 SVD를 통해 풀어 $b$를 구한다.

강의

• Plane-based calibration: https://youtu.be/4-thTdR7Blg?t=3357
• Stereo rig calibration: https://youtu.be/DDjfhYxqp3w
• Slides: http://www.ipb.uni-bonn.de/html/teaching/photo12-2021/2021-pho1-22-Zhang-calibration.pptx.pdf

Reference

• https://angeloyeo.github.io/2021/06/17/Cholesky_decomposition.html