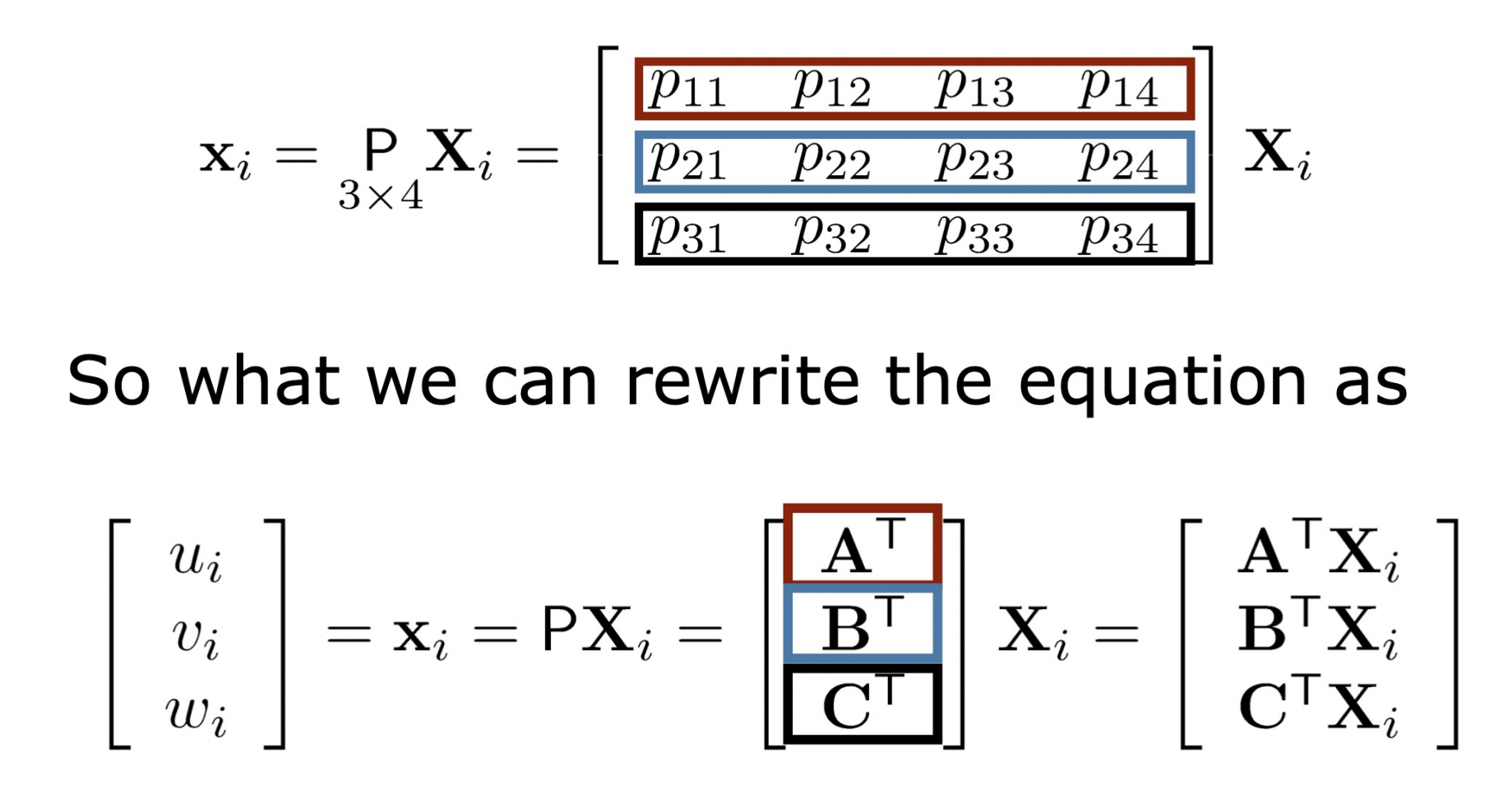Direct Linear Transformation(DLT)

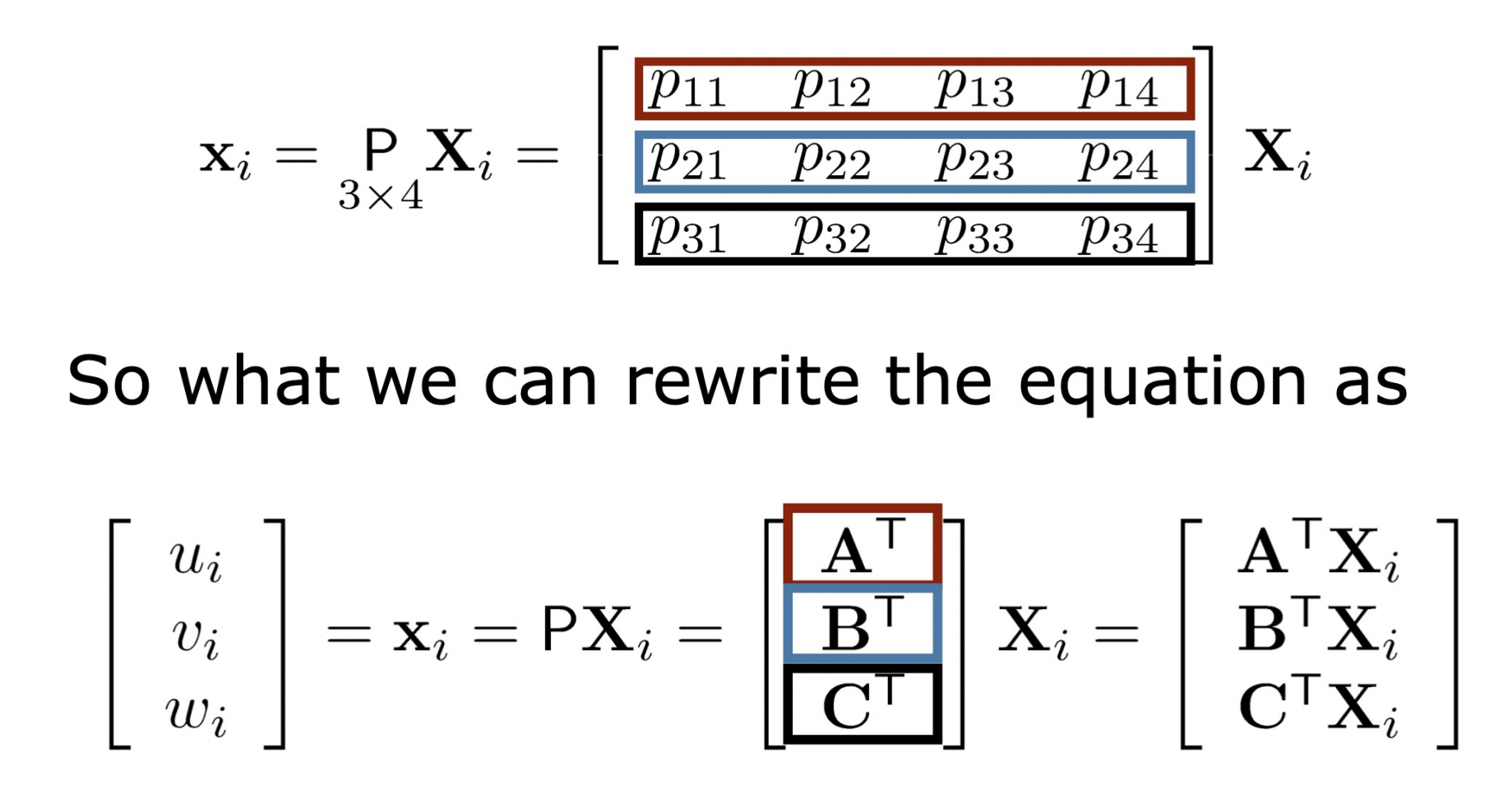
Estimating the Parameters of P

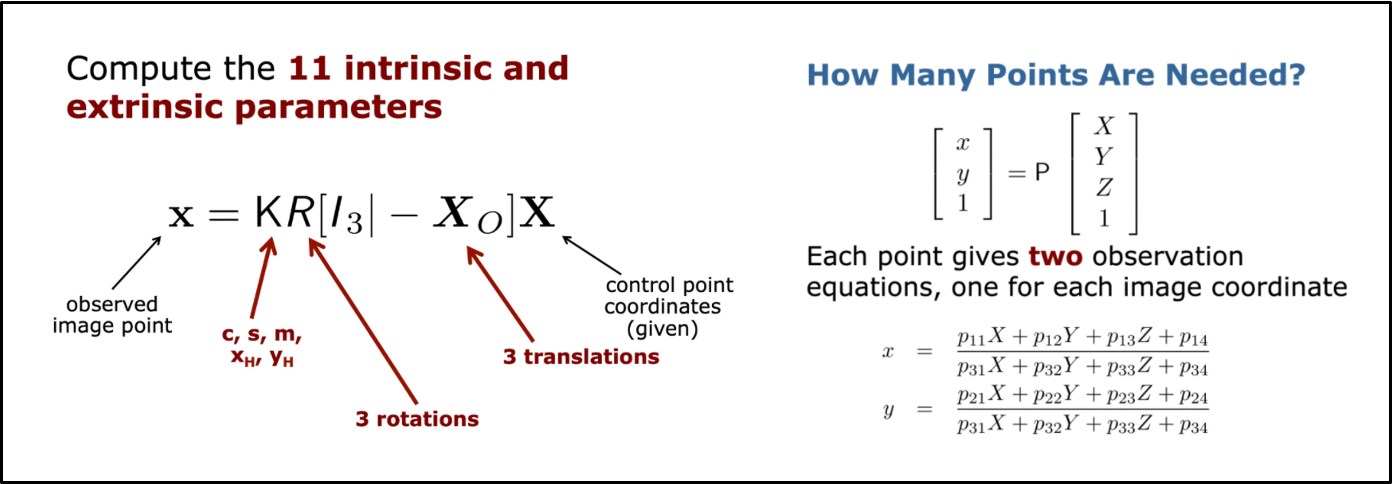
• World 좌표계로부터 image plane 상의 2D point를 구하기 위해서는 5개의 intrinsic parameters와 6개의 extrinsic parameters가 필요하다.
• 하나의 매칭쌍으로부터 2개의 식이 도출되므로 최소 6쌍의 매칭점이 필요하다.

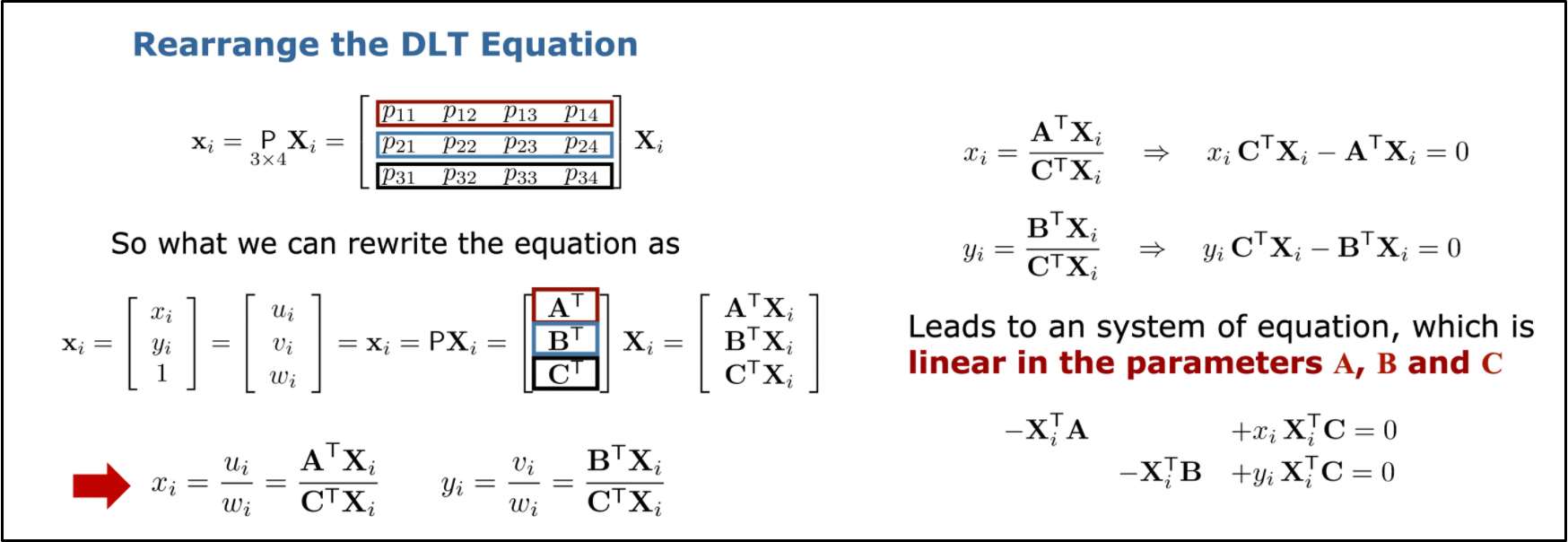
• 행렬 $P$의 각 행을 $A,B,C$ 벡터로 치환하고 식을 풀면 $A,B,C$에 대한 선형식을 얻을 수 있다.

• $A,B,C$를 stacking하여 12x1의 열벡터 $p$로 만들어주고 선형식의 계수에 해당하는 부분을 $a_{x_i}^T, a_{y_i}^T$로 표기한다.
• $I$개의 매칭쌍을 stacking하여 표기하면 $2I \times 12$의 행렬 $M$으로 나타낼 수 있으며 $Ax=0$의 형태가 나와 SVD를 통해 풀 수 있다.

• 하지만 우변은 오차들로 인해 0이 아니 $w$값을 가지게 되며 따라서 우리의 목표는 $w^Tw$를 최소화하는 $p$를 찾는 것이 된다.
• SVD를 통해 $M$을 분해하며 singular value는 내림차순으로 정리되어 있으므로 가장 작은 singular value를 가지는 $v_{12}$가 $w^Tw$를 최소화하는 벡터가 된다.

Decomposition of P

• $H=KR, h=-KRX_O$로 정의하면 $P=[H|h]$로 표현되며 $X_O$ 또한 두 식의 연립으로 $-H^{-1}h$로 구할 수 있다.
• $K$는 upper triangular matrix이고 $R$은 orthogonal matrix이므로 QR분해를 활용할 수 있으나 두 matrix의 순서가 반대되므로 변형식이 필요하다.
• $K^{-1}$과 $R^{-1}$ 모두 upper triangular과 orthogonal이라는 특성을 유지하므로 $H^{-1}$를 QR분해하여 $K$와 $R$을 도출할 수 있다.