Projective Transformation

• 3D world에서의 object를 이미지로 mapping 하는 것은 projective transformation의 하나의 예시이다.
• 이미지 상에서 사각형은 사각형이 아니고 원은 원이 아니며 평행한 선이 어떤 점에서 만나게 된다.즉, 각도, 거리, 거리비 등 geometric한 특성이 보존되지 않는다.
• 단, straightness는 유지된다. 직선은 mapping 해도 직선이다.

Euclidean vs Projective

• Euclidean geometry는 synthetic geometry의 예로 컴퍼스나 자를 이용하는 axiomatic(자명한) 방식이다.
• Projective geometry는 coordinate과 algebra를 이용하는 anlytic geometry이며 infinity를 표현할 수 있다.

Homogenous Coordinates

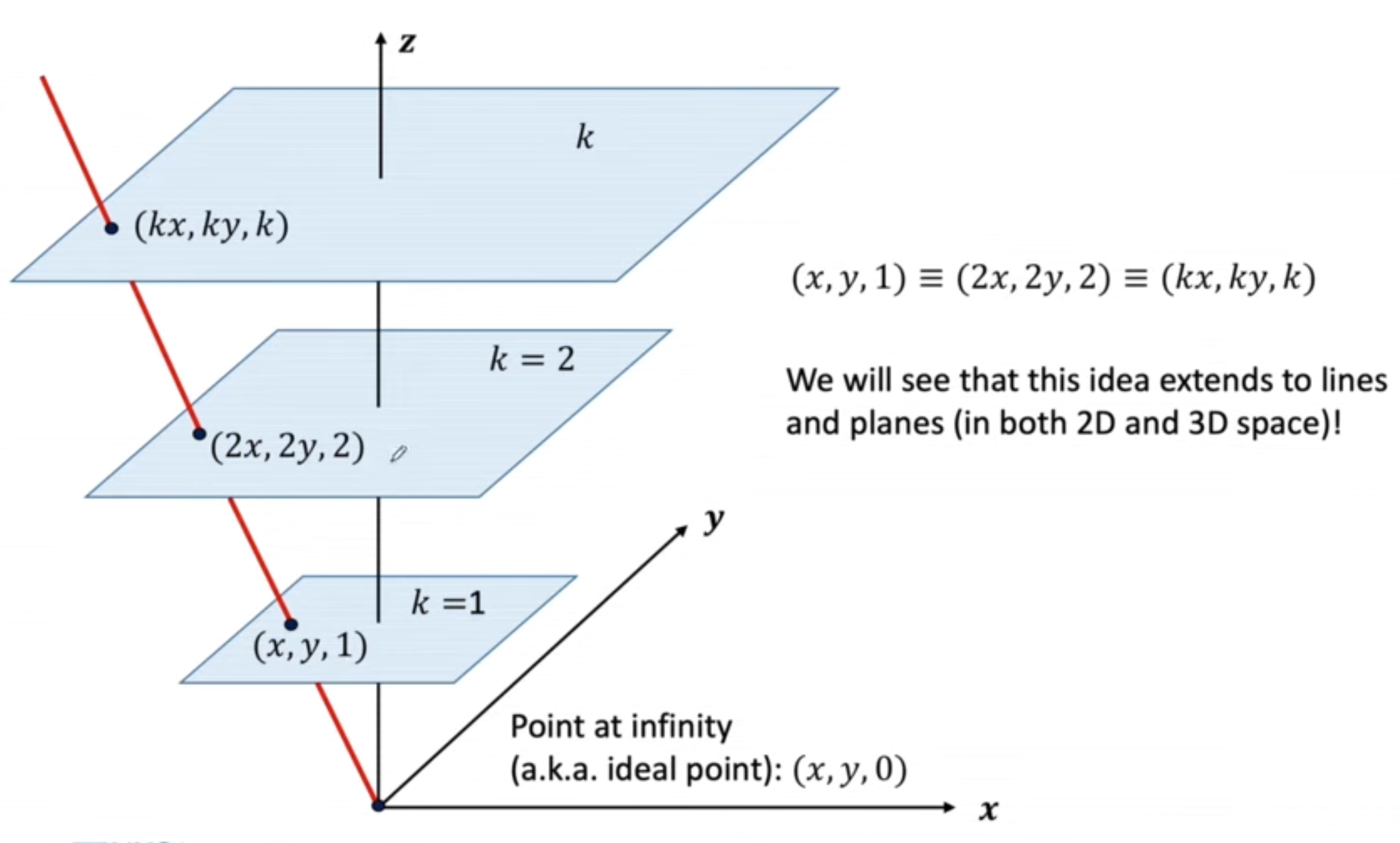
• Homogenous 좌표 $(kx, ky, k)$는 cartesian 좌표 $(\cfrac{kx}{k},\cfrac{ky}{y})=(x,y)$와 같으며 모든 $k$에 대해 동일하다.
• $k=0$ 일 때 $(\cfrac{x}{0},\cfrac{y}{0})$이므로 point at infinity(ideal point)를 의미하게 된다.
• Euclidean space $\mathbb{R}^n$이 projective space $\mathbb{P}^n$으로 확장된다고 볼 수 있다.

The 2D Projective Plane

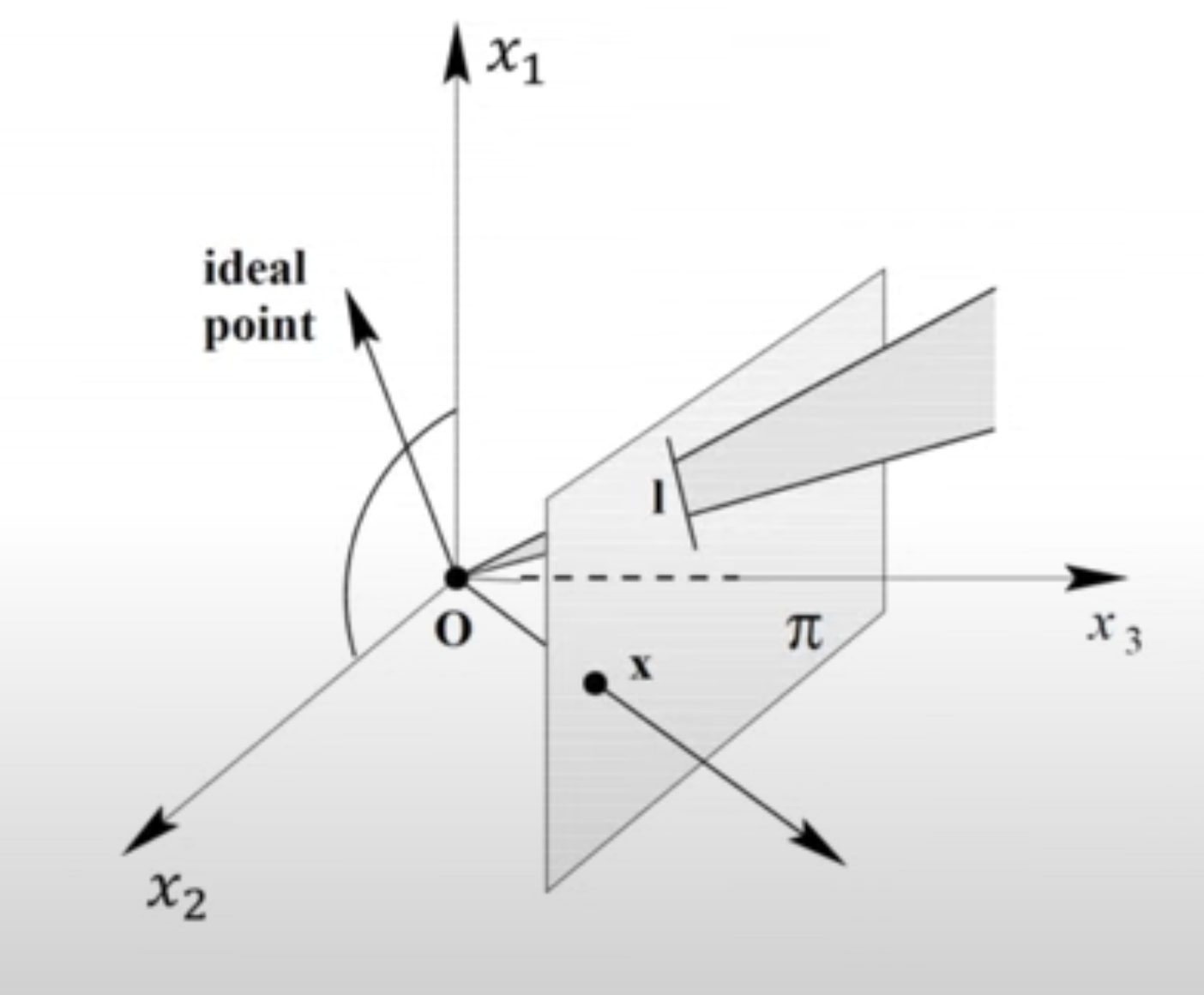
• Plane에 있는 line은 $ax+by+c=0$으로 표현된다. 변형하면 $y=-\cfrac{a}{b}x-c$로 익숙한 선에 대한 방정식 형태가 된다.
• 따라서 line은 벡터 $(a,b,c)^T$로 표현할 수 있다.

Homogenous Representation of Lines and Points

• $ax+by+c=0$과 $(ka)x+(kb)y+(kc)=0$은 동일하기 때문에 벡터 $(a,b,c)^T$와 line은 one-to-one이 아니다.
• 하나의 point $\mathbf{x}=(x,y)^T$는 $ax+by+c=0$을 만족할 때만 line $\mathbf{l}=(a,b,c)^T$ 상에 존재한다.
  $(x,y,1)(a,b,c)^T= \mathbf{x}^T\mathbf{l} = 0$
• Point는 $x,y$ line은 $a:b:c$의 두 개의 ratio로 각각 2 DoF를 가진다.
• 0이 아닌 $k$에 대해서도 동일하다.
  $(kx,ky,1)(a,b,c)^T=k(x,y,1)\mathbf{l}=0$
• 따라서, 다양한 $k$에 대해 $(kx, ky, k)^T \in \mathbb{P}^2$는 point $(x,y)^T \in \mathbb{R}^2$의 representation이다.
  $\mathbb{x}=(x_1,x_2,x_3)^T \in \mathbb{P}^2 \equiv(\cfrac{x_1}{x_3},\cfrac{x_2}{x_3})^T \in \mathbb{R}^2$

Intersection of Lines

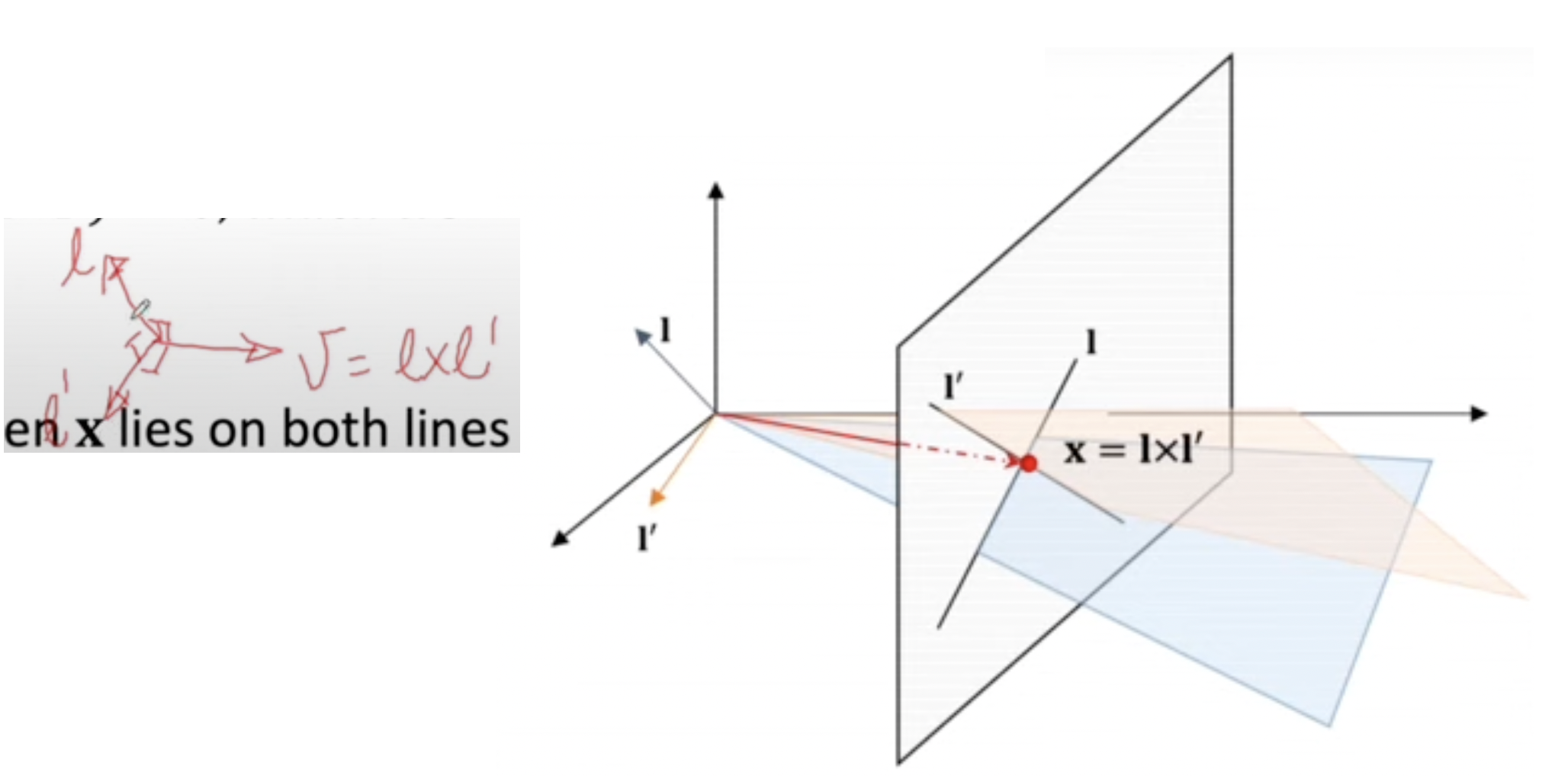
• 두 line의 intersection은 point로 외적으로 구할 수 있다.
  $\mathbf{x =l\times l'}$
• Homogeneous 좌표로 볼 때 두 line에 대해 orthogonal하다.
• Triple scalar product identity로 증명하면 $\mathbf{l.(l \times l')=l'.(l \times l')=0}$이므로 $\mathbf{l^Tx=l'^Tx=0}$
  두 line에 직교하는 벡터는 $\mathbf{l, l'}$과 orthogonal하기 때문에 내적했을 때 0이다.
  * $||a||||b||cos\theta = a \cdot b$를 통해 직교할 때 내적이 0임을 증명 가능하다.

Line Joining Points

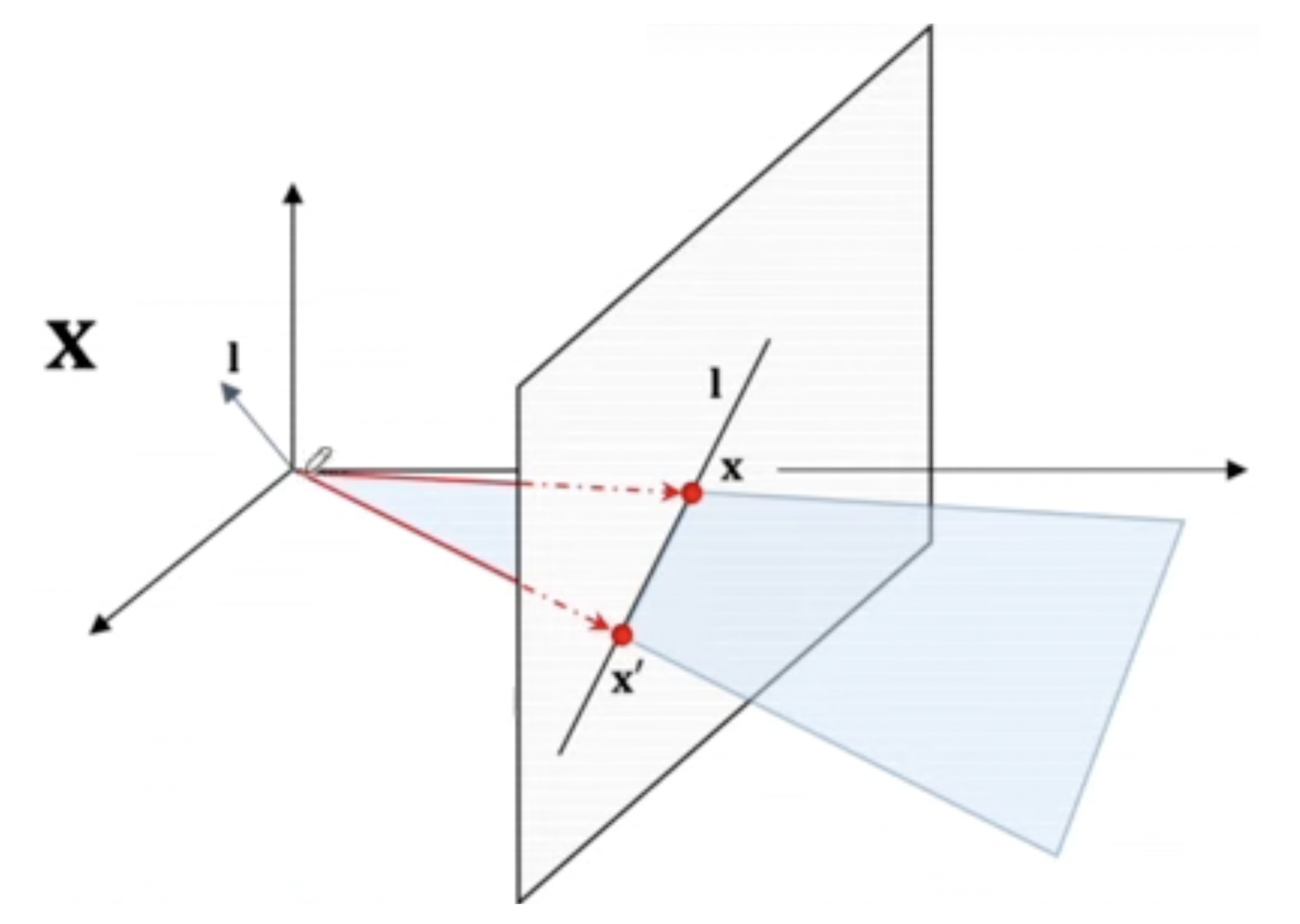
• 두 point $\mathbf{x, x'}$의 외적을 통해 이들을 통과하는 line을 구할 수 있다.
  $\mathbf{l=x \times x'}$
• 위 증명과 마찬가지로 $\mathbf{x.(x \times x')=x'.(x \times x')=0}$이므로 $\mathbf{x^Tl=x'^T=0}$
• $\mathbf{l}$이 그림의 plane 상에 맺히는 line이 어떻게 되나 직관적으로 이해하기 어려웠는데 point와 달리 $ax+by+c=0$을 만족하는 $(x,y)$들의 집합이기 때문에 그런듯하다.

Ideal Points and the Line at Infinity

• 평행한 두 line이므로 $ax+by+c=0$과 $ax+by+c'=0$으로 표현할 수 있다.
• $\mathbf{l}=(a,b,c)^T, \mathbf{l'}=(a,b,c')^T$를 외적하여 intersection을 구해보면 $\mathbf{l \times l'}=(c'-c)(b,-a,0)^T$로 scale factor $(c'-c)$를 무시하게 된다.
• $(b,-a,0)^T$은 infinite point가 되며 평행한 두 line은 infinity에서 만난다고 할 수 있다.
• Inhomogeneous notation $(b,-a)^T$는 line에 접하며 line normal $(a,b)$에 orthogonal하므로 line의 방향을 나타낸다.
• Line의 방향은 다양하므로 ideal point $(b, -a, 0)^T$는 다양하고 따라서 line at infinity는 line의 방향의 집합이라 할 수 있다.

Reference

• https://www.youtube.com/watch?v=LAHQ_qIzNGU&list=PLxg0CGqViygP47ERvqHw_v7FVnUovJeaz&index=1&t=2027s