1. Scaling Up Graph Neural Networks to Large Graphs
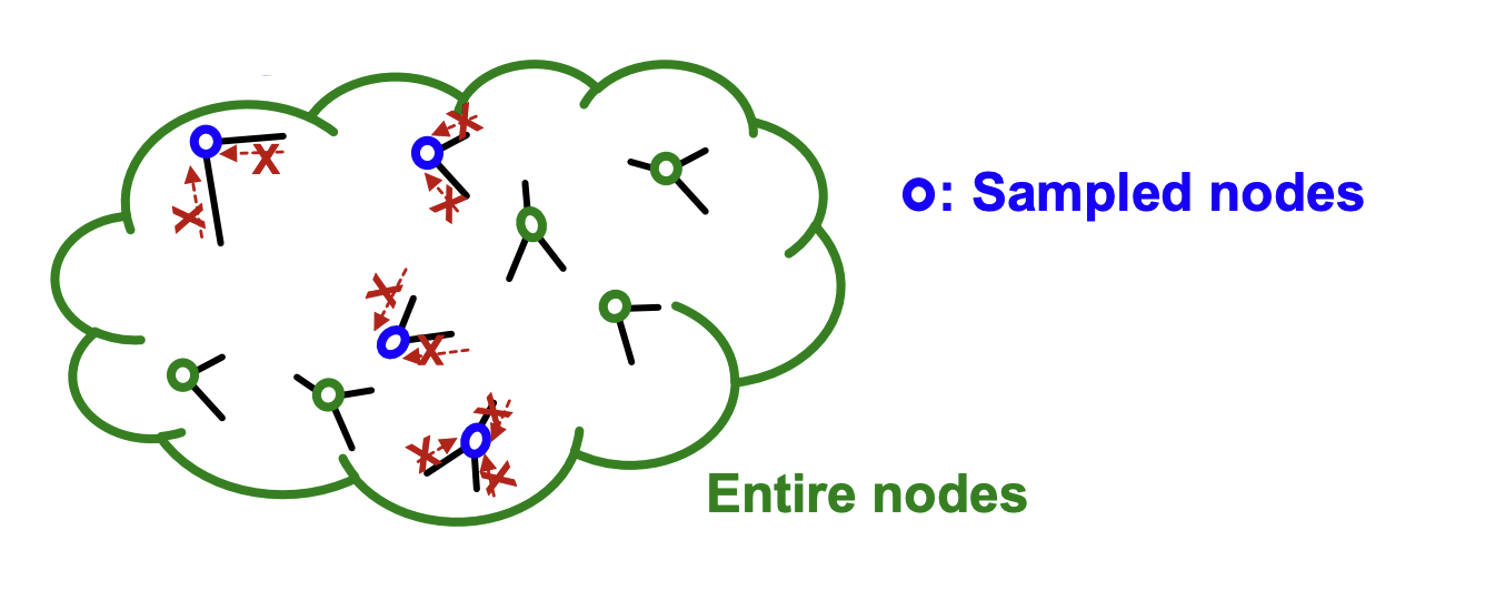
- Recommender systems, social network,academic graph, knowledge graph 등 다양한 분야에 large-scale의 그래프가 활용되고 있다.
- 일반적으로 ML 모델은 미니배치를 활용한 SGD를 통해 학습을 한다.
- 이웃노드들로부터 message를 전달받는 GNN에서는 미니배치를 활용해 일부 노드만 샘플링하는 것이 불가능하다.
- Full-batch 또한 GPU의 병렬연산을 효과적으로 활용할 수 없기 때문에 어렵다.
2. GraphSAGE Neighbor Sampling: Scaling up GNNs
Stochastic Training
-
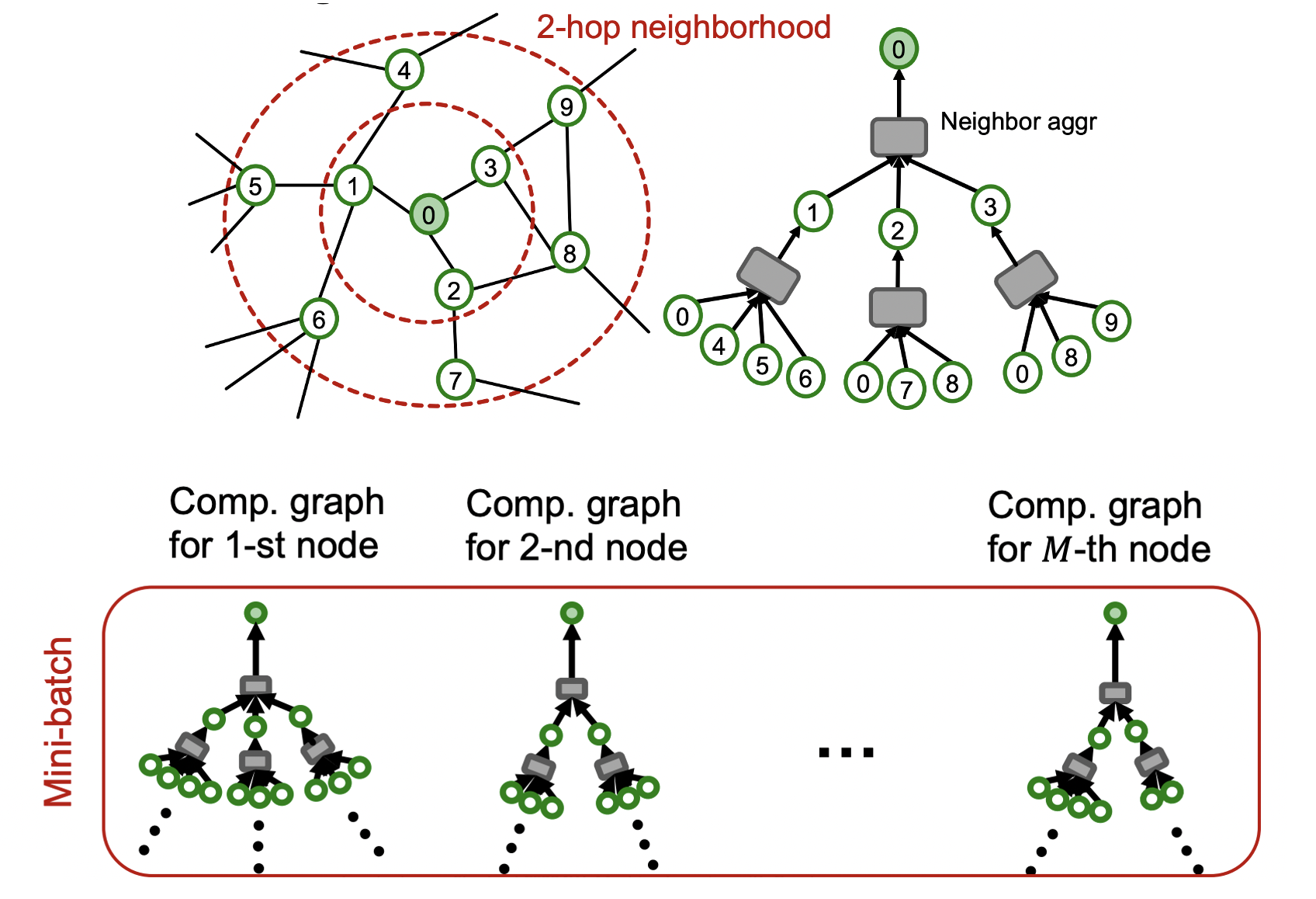
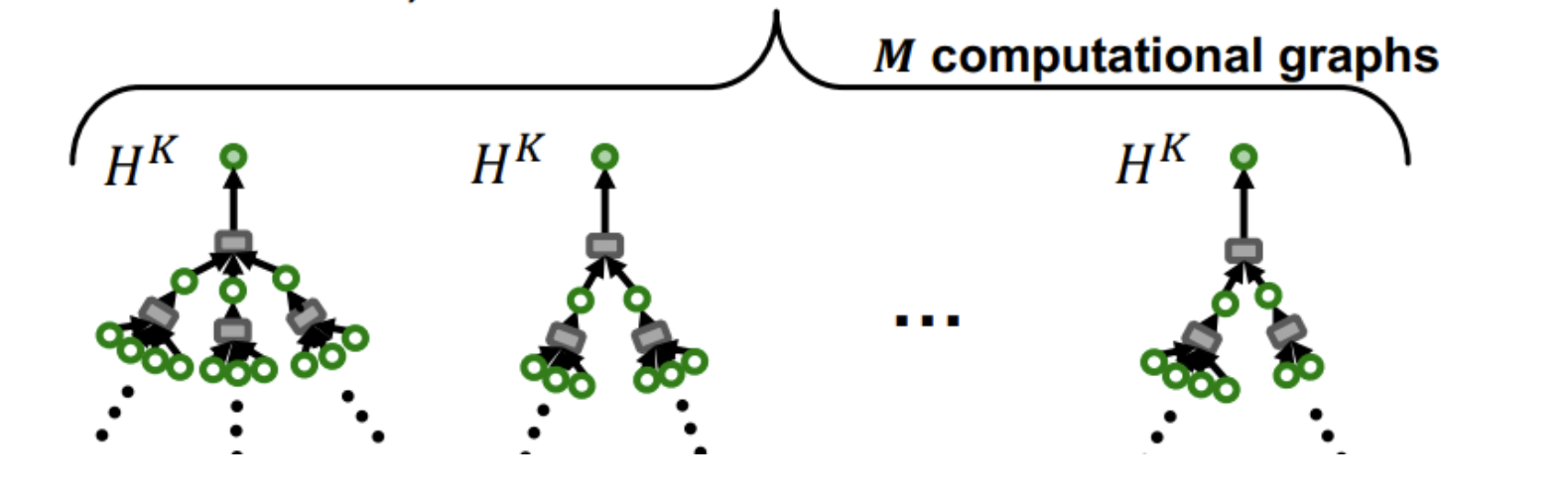
K-layer의 GNN은 K-hop 이웃노드들의 feature를 전달 받은 노드의 임베딩을 만든다.
-
개의 노드는 개의 computational graphs로 나타낼 수 있으므로 mini-batch를 구성할 수 있다.
-
개의 노드에 대한 평균 loss 를 SGD를 통해 학습한다.
-
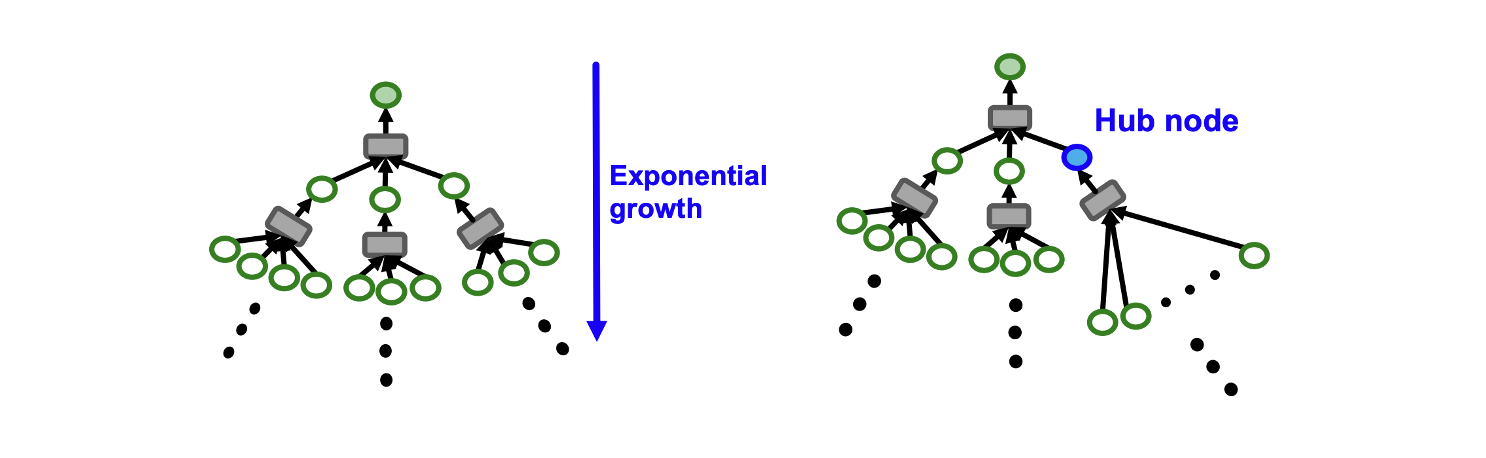
Computational graph에 대한 SGD는 모든 노드에 대한 K-hop neighbor를 aggregation 하는 과정에서 연산량이 지수적으로 증가한다는 문제가 있다.
-
또한, high-degree를 가지는 hub node가 있을 때 연산량이 급증한다.
Neighbor Sampling
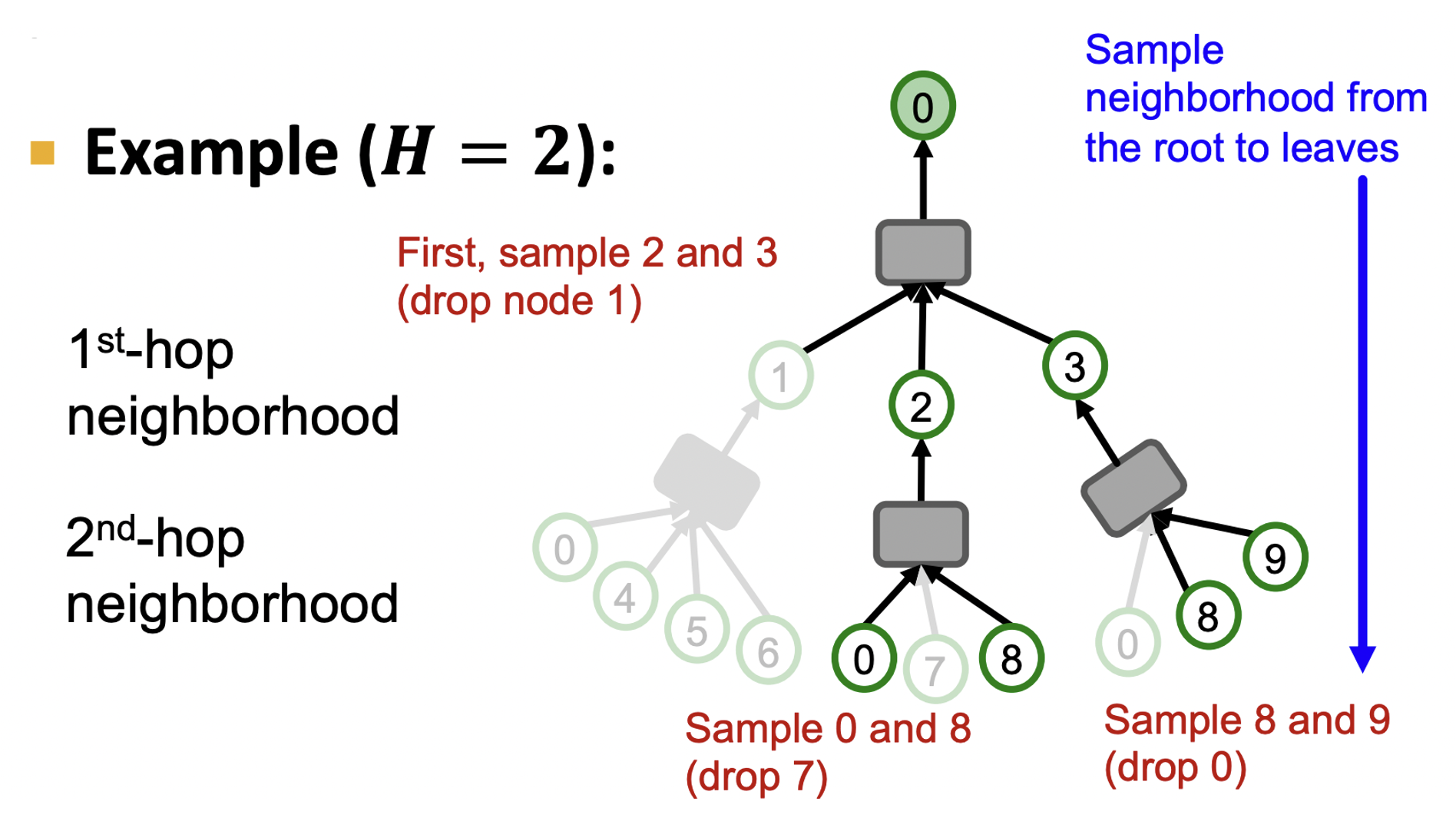
- 각 hop에서 개의 이웃 노드를 샘플링하여 computational graph를 구성할 수 있다.
- 가 작을 경우 연산량은 줄지만 variance가 커 학습이 불안정하다는 trade-off가 있다.
- 샘플링을 랜덤하게 할 경우 빠르지만 optimal하지 못하다.
- Random Walk with Restarts score 를 구해 중요한 노드들을 샘플링하면 더 효과적일 수 있다.
Issues with Neighbor Sampling

- Neightbor Sampling은 GNN layer 수에 따라 computational graph의 크기가 지수적으로 증가한다.
- 또한, 미니배치의 노드들이 많은 이웃을 공유할 경우 불필요한 연산을 하게 된다.
Cluser-GCN: Scaling up GNNs
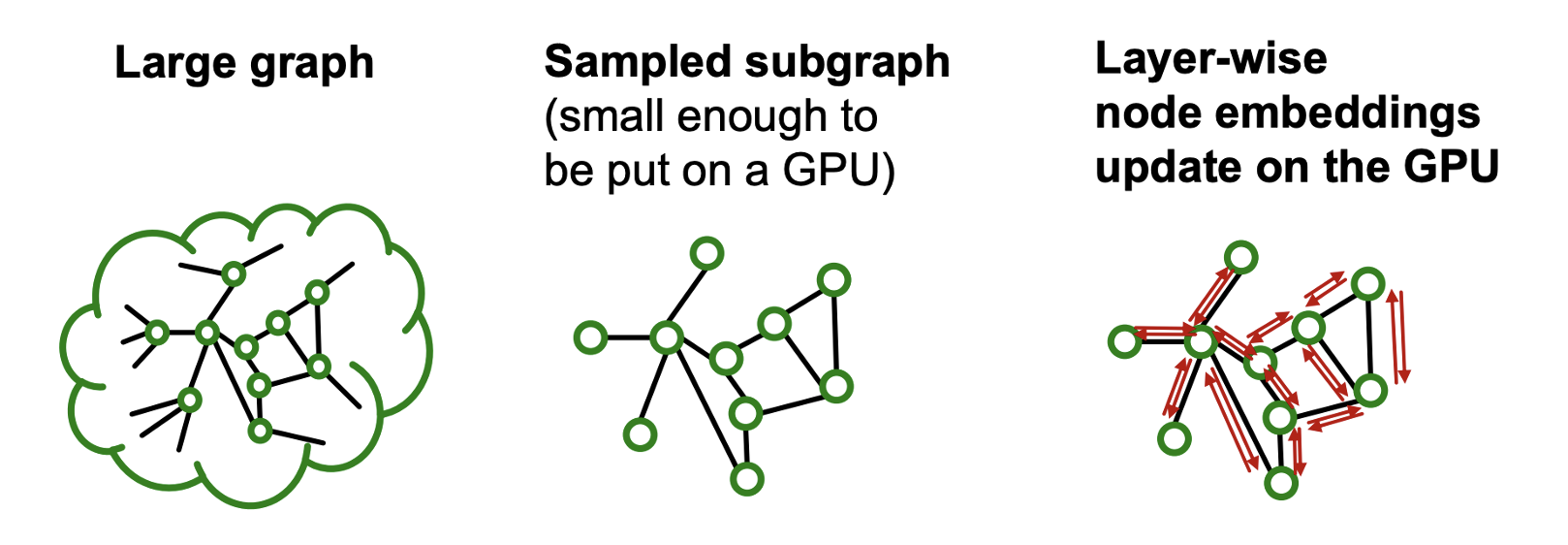
- Layer-wise node embedding update는 이전 레이어에서의 임베딩을 재사용하기 때문에 neighbor sampling의 불필요한 연산을 줄여준다.
- 하지만, large graph에서 GPU 메모리의 한계가 있다.
- 단점을 없애고 장점을 살리기 위해 subgraph를 샘플링하여 활용할 수 있다.
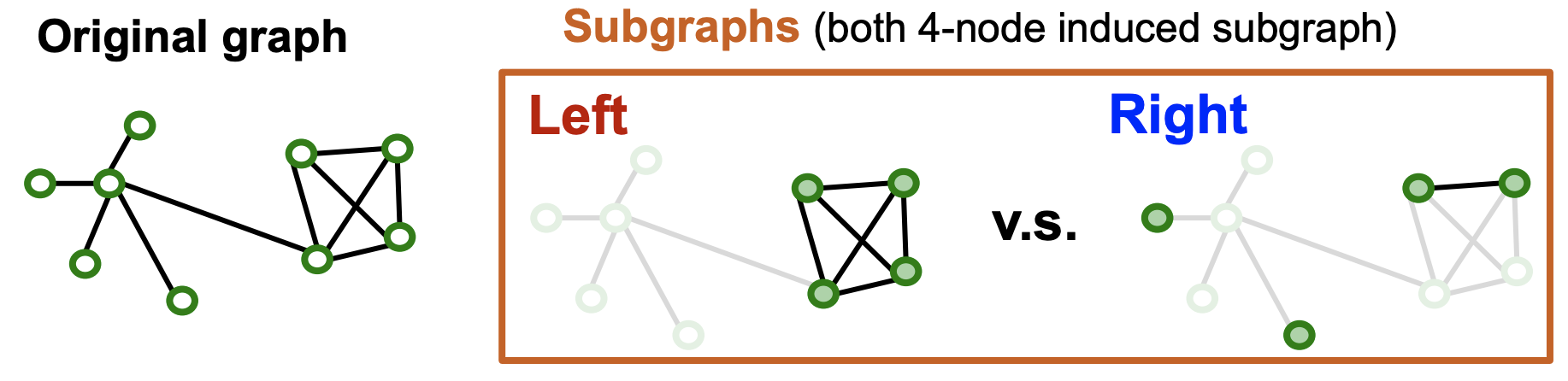
- 엣지들이 많이 사라져 노드들이 고립되는 subgraph는 좋지 못하다.
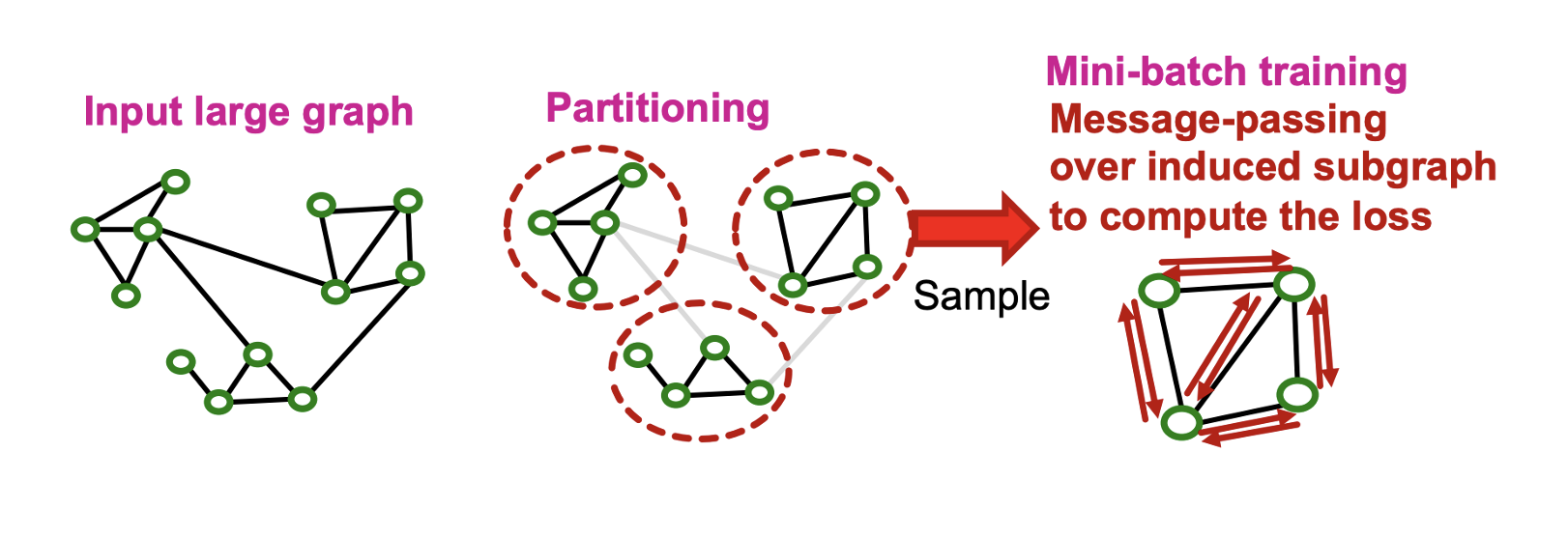
- Real-world graph는 community structure를 가지며 community를 샘플링 하기 위해 Cluster-GCN을 활용한다.
- Cluster-GCN은 larget graph를 그룹화하는 pre-processing 과정과 샘플링한 그룹 내에서 message passing을 하는 mini-batch training 과정으로 나뉜다.
Pre-process
- Pre-processing 과정에서는 Louvain, METIS, BigCLAM 등 community detection 알고리즘을 활용해 를 노드에 대해서만 로 그룹화한다. 엣지는 포함되지 않는다.
Mini-batch training
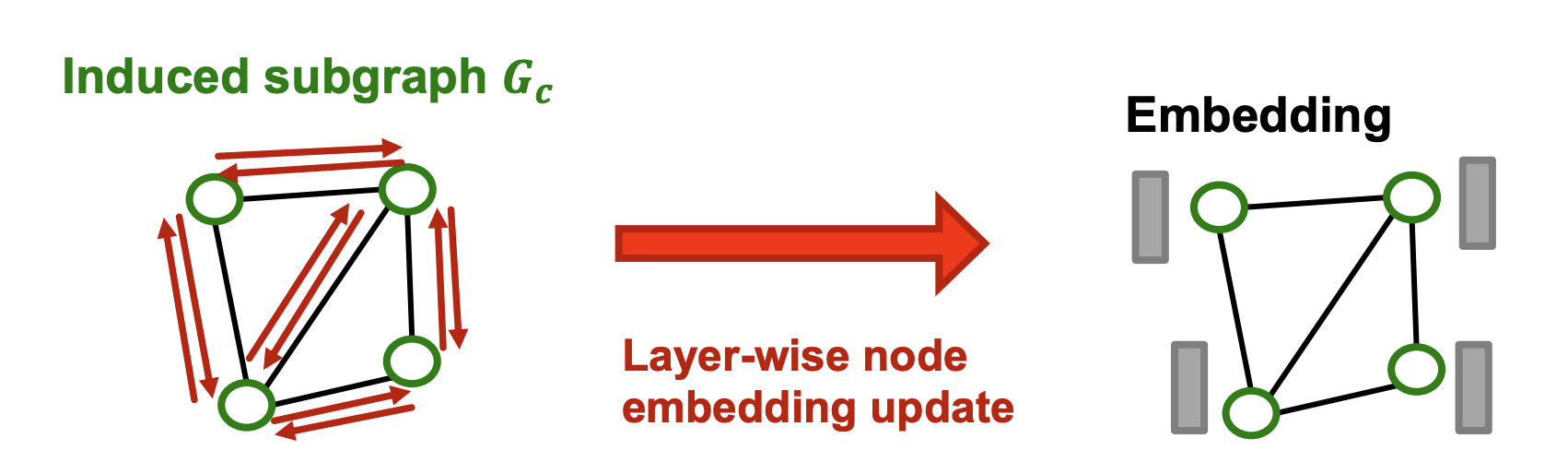
- 샘플링한 노드 그룹 로부터 엣지가 있는 induced subgraph 를 만든다.
- Layer-wise node update를 적용하여 각 노드 에 대한 임베딩 를 얻고 loss를 통해 업데이트한다.
Issues with Cluster-GCN
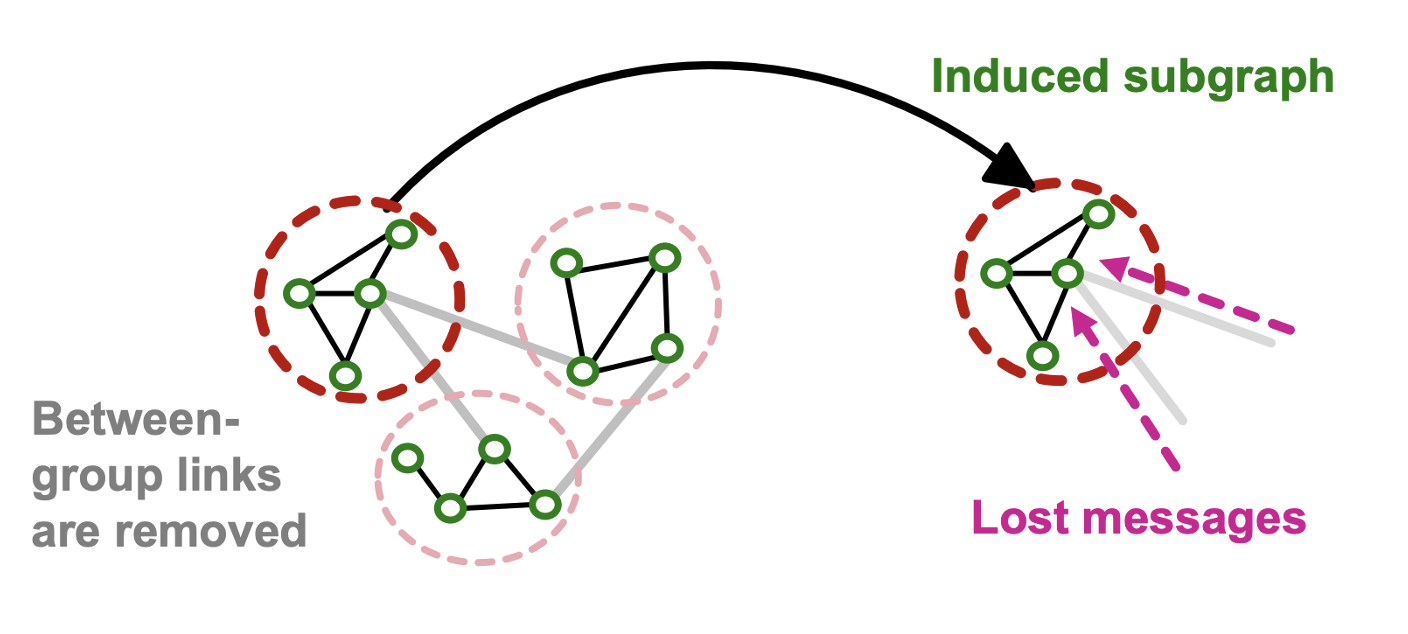
- Induced subgraph는 그룹 간의 엣지를 제거하여 message를 잃는다.
- Community detection 알고리즘은 유사한 노드들끼리 하나의 그룹으로 묶어 샘플링된 그룹은 전체 데이터의 작은 부분만을 커버할 수 있다.
- 샘플링된 노드가 전체 구조를 표현하기에 충분히 다양하지 못하다.
Advanced Cluster-GCN
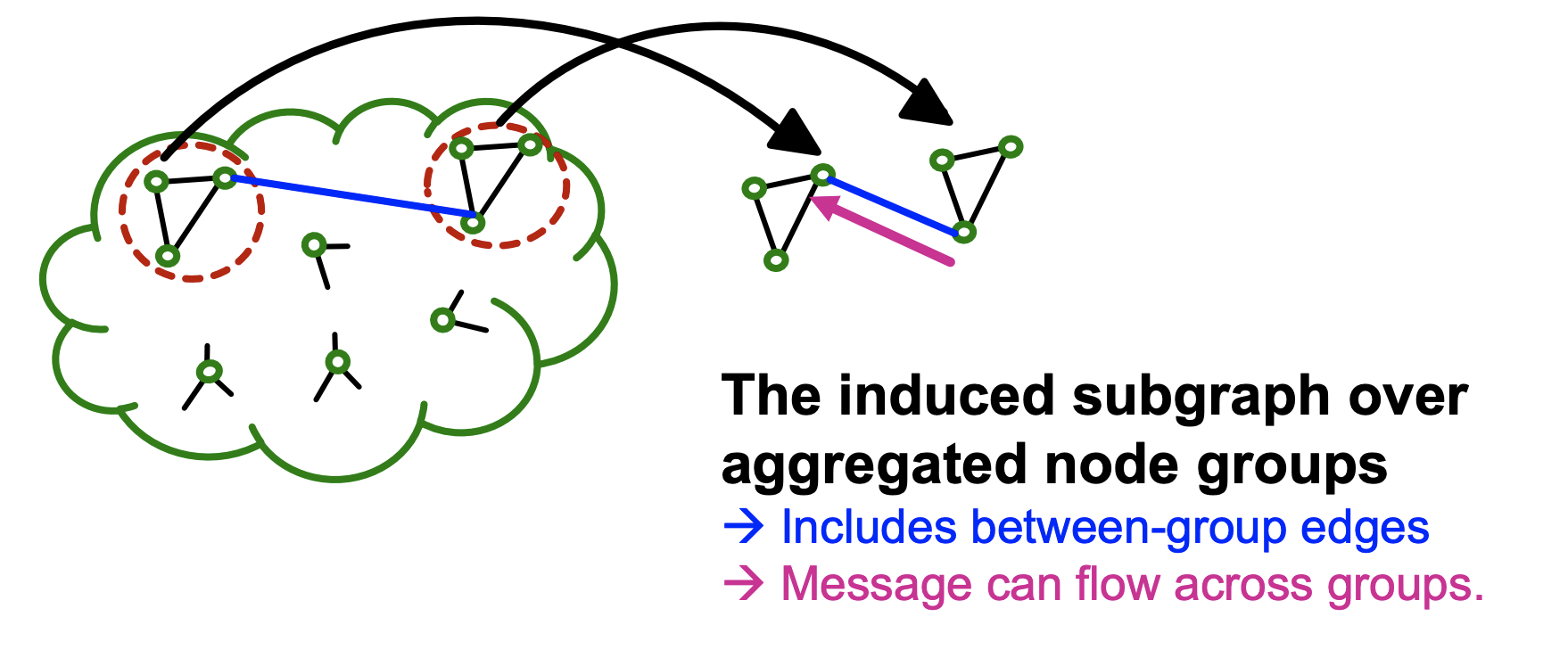
- 상대적으로 적은 수의 그룹을 만들고 여러 개의 노드 그룹을 미니배치 단위로 합친다.
- Vanila cluster-GCN과 동일하게 pre-processing 과정에서는 그룹화하되 상대적으로 적은 수의 그룹으로 나눈다.
- Mini-batch training에서는 개의 노드 그룹을 랜덤하게 골라 합치고 induced subgraph를 만들어 학습한다.
Comparison of Time Complexity
- Neighbor sampling은 각 레이어에서 개의 이웃노드를 샘플링하기 때문에 하나의 노드에 대해 이며, 개의 노드 임베딩을 생성하기 위해서는 의 시간복잡도가 든다.
- Cluster-GCN은 개의 노드에 대해 induced subgraph를 만들고 는 평균 node degree, 는 레이어의 수라 할 때 시간복잡도는 가 된다.
- Cluster-GCN의 시간복잡도는 선형적으로 증가하므로 효율적이지만 가 크지 않다면 neighbor sampling을 주로 쓴다.
3. Sacling up by Simplifying GNNs
Recall
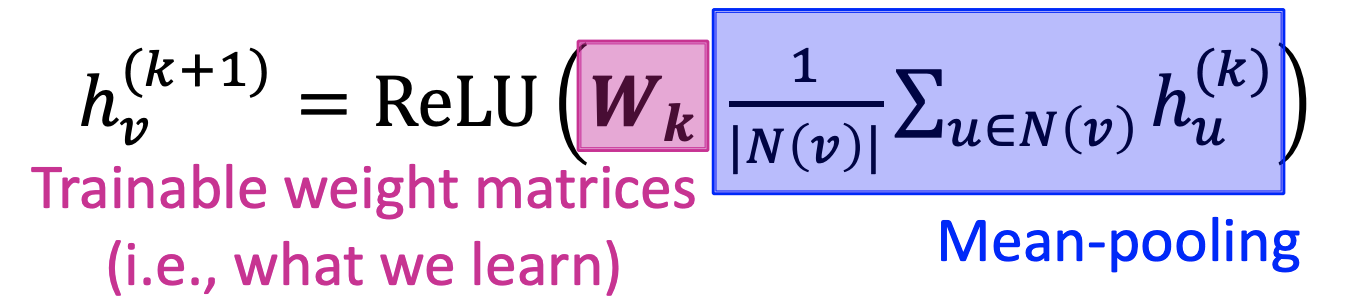
-
Self-loop를 포함하는 와 로 이루어진 그래프의 node feature가 라 할 때 input node embedding은 이다.
-
Mean-pooling을 활용하면 은 이웃노드들의 정보를 평균낸 것을 학습되는 파라미터 에 곱한 후 ReLU를 거쳐 구할 수 있다.

-
Matrix form으로 나타내면 위와 같다.
-
,
-
인접행렬
-
-
노드 의 degree가 담긴 대각행렬
Simplifying GCN
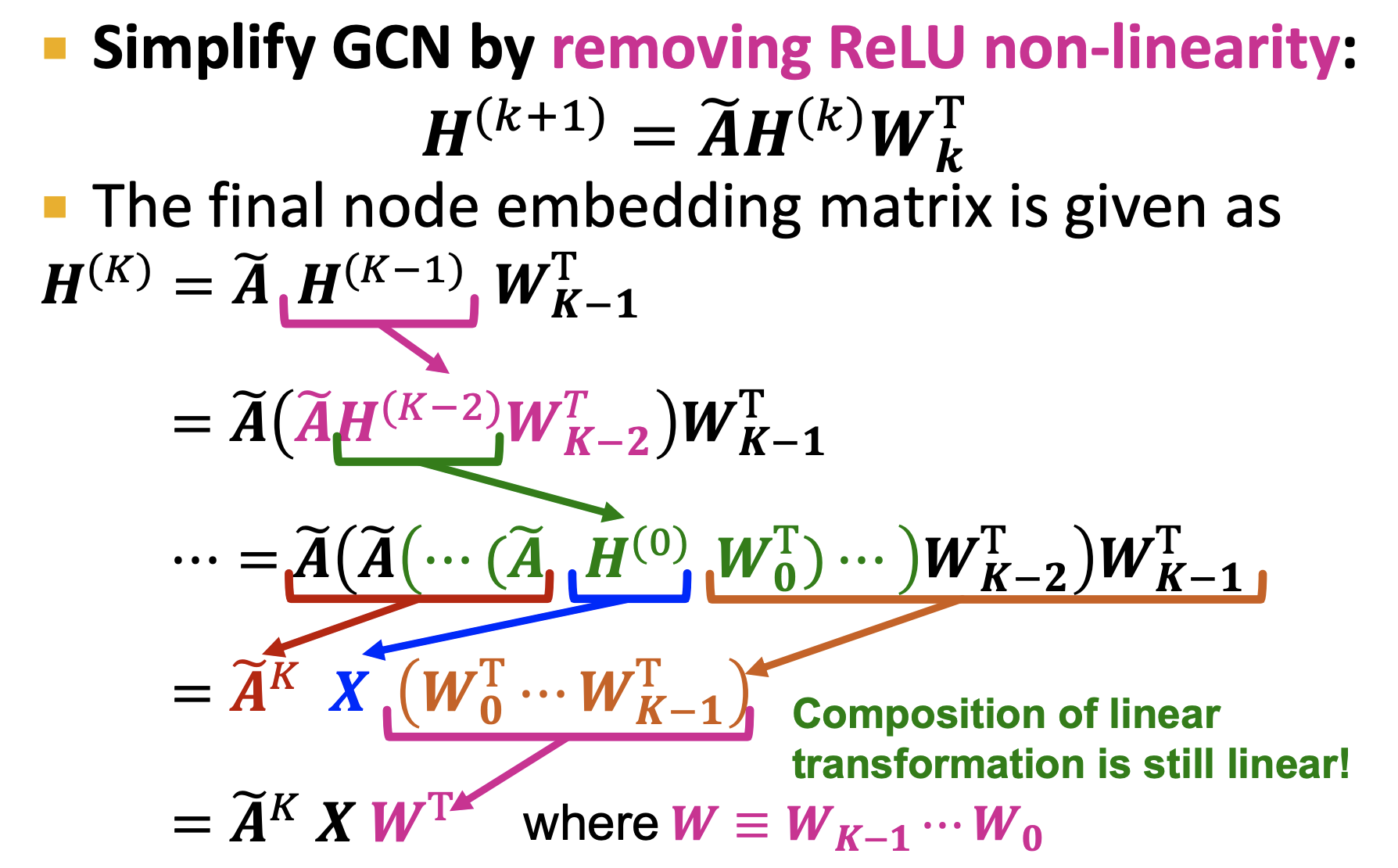
- GCN에서 non-linear activation을 제거하여 simplify 할 수 있다.
- 에는 학습되는 파라미터가 없으므로 미리 계산할 수 있다.
- 라 하면 최종 임베딩은 가 된다.
- 가 미리 계산되므로 개의 노드의 임베딩은 에 linear한 시간복잡도를 가진다.
,
,
- Pre-processing 과정에서는 가 CPU로 계산된다.
- Min-batch training 과정에서는 개의 노드가 랜덤하게 샘플링되어 임베딩 가 계산된다. 임베딩을 통해 예측한 값과의 loss로 parameter를 업데이트 한다.
Comparison with Other Methods
- Neighbor sampling에 비해 노드 임베딩을 더 효율적으로 만들며 Cluster-GCN처럼 그룹을 활용하지 않기 때문에 전체 노드로부터 완전히 랜덤하게 샘플링하여 variance를 줄일 수 있다.
- 하지만, non-linearity가 없어 기존 GNN 모델에 비해 표현력이 떨어진다는 한계가 있다.
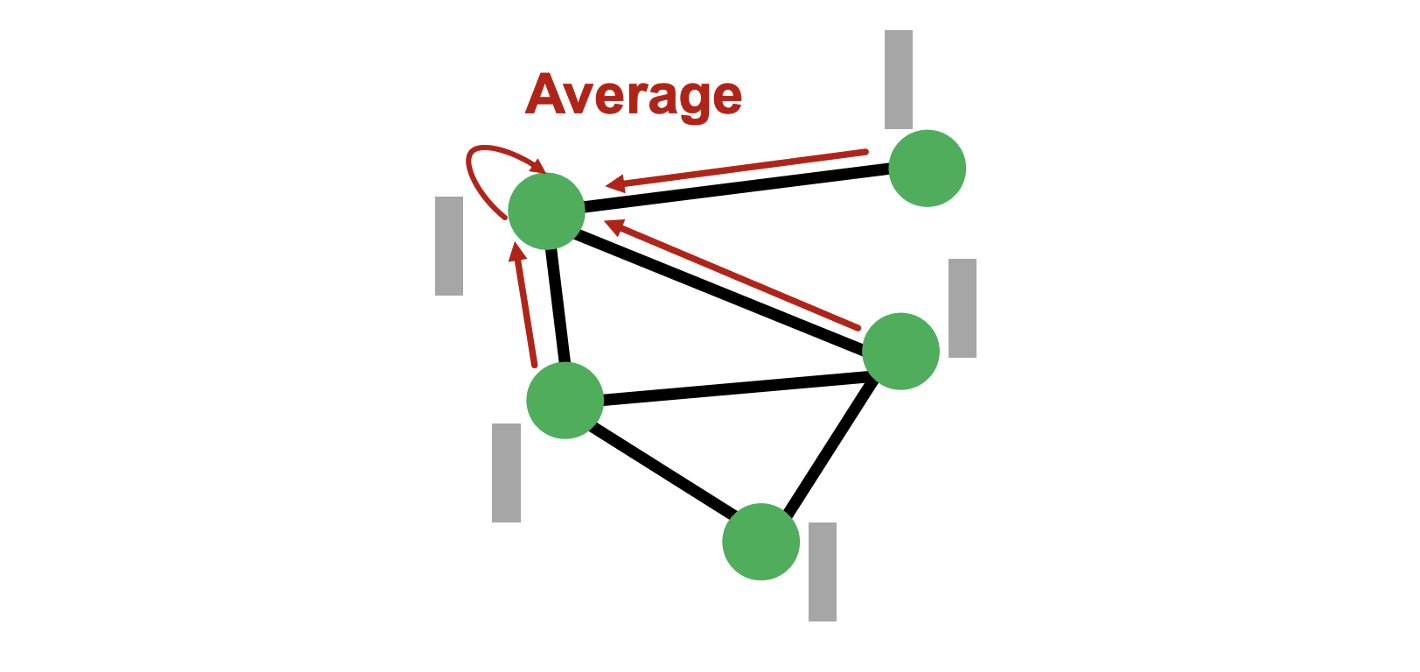
- 그럼에도 불구하고 많은 node classification task에서 연결된 노드들이 동일한 target label을 가지는 homophily structure를 보이기 때문에 original GNN과 유사한 성능을 보인다.
(ex. Social network에서 두 사람이 친구인 경우 같은 영화를 좋아하는 경향이 있다) - Pre-processing 과정에서 feature는 반복적으로 이웃 노드의 feature를 평균내 얻으므로 연결된 노드들이 유사한 feature를 가지고 이는 homophily structure 하에서 잘 작동한다.
References
- Lecture 17.1: https://www.youtube.com/watch?v=2nPCw3yHlnI&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=53
- Lecture 17.2: https://www.youtube.com/watch?v=LLUxwHc7O4A&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=54
- Lecture 17.3: https://www.youtube.com/watch?v=RJkR8Ig6dXI&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=55
- Lecture 17.4: https://www.youtube.com/watch?v=iTRW9Gh7yKI&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=56
