1. Limitations of GNN
Problems & Solustions
- 완벽한 GNN 모델이란 neighborhood structure와 node embedding 사이에 injective function을 가지는 것을 의미한다.
- 즉 같은 구조라면 같은 노드 임베딩을, 다른 구조라면 다른 노드 임베딩을 가져야 한다.
- Problem 1: 같은 구조를 가지더라도 그래프 상에서 다른 위치에 있어 다른 임베딩을 가지기를 원할수도 있다

- Problem 2: 지금까지 배운 GNN은 완벽하지 못하다. 예를 들어, message passing GNN은 cycle length를 세지 못해 과 가 다른 구조임에도 불구하고 같은 computational graph를 가진다.(Lecture 9 WL test)
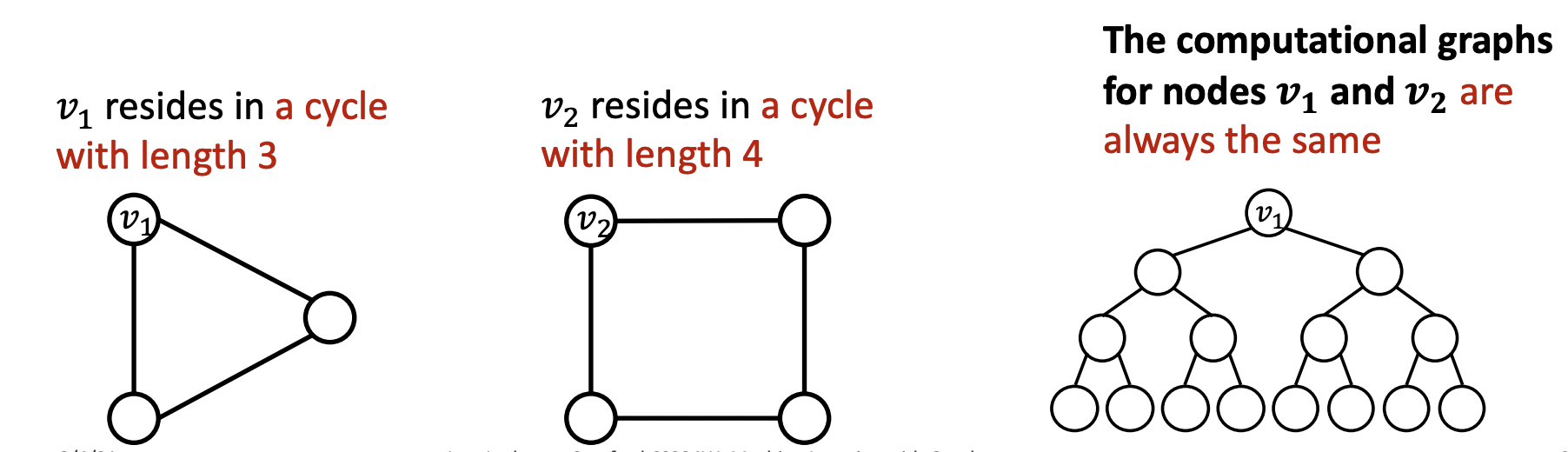
- Solution: 위치를 고려한 Position-aware GNNs, WL test보다 표현력이 뛰어난 Identity-aware GNNs
Naive Approach
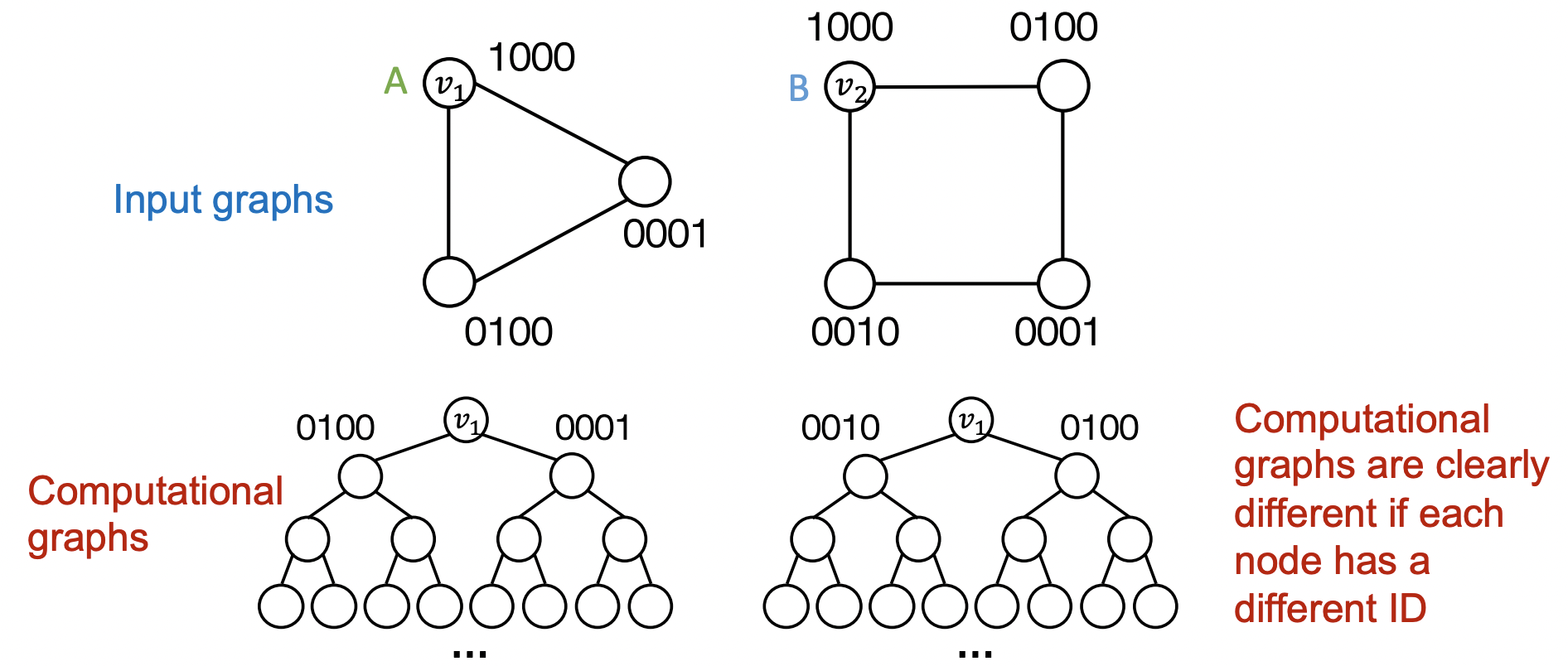
- 서로 다른 input(nodes, edges, graphs)에 대해 다르게 라벨링 되어야 한다.
- 원핫 인코딩을 통해 각 노드를 다른 ID로 인코딩하는 방식을 생각해볼 수 있지만 의 feature dimension이 필요하며 새로운 노드/그래프에 대해 일반화할 수 없다는 문제가 있다.
2. Position-aware Graph Neural Networks
Two types of tasks
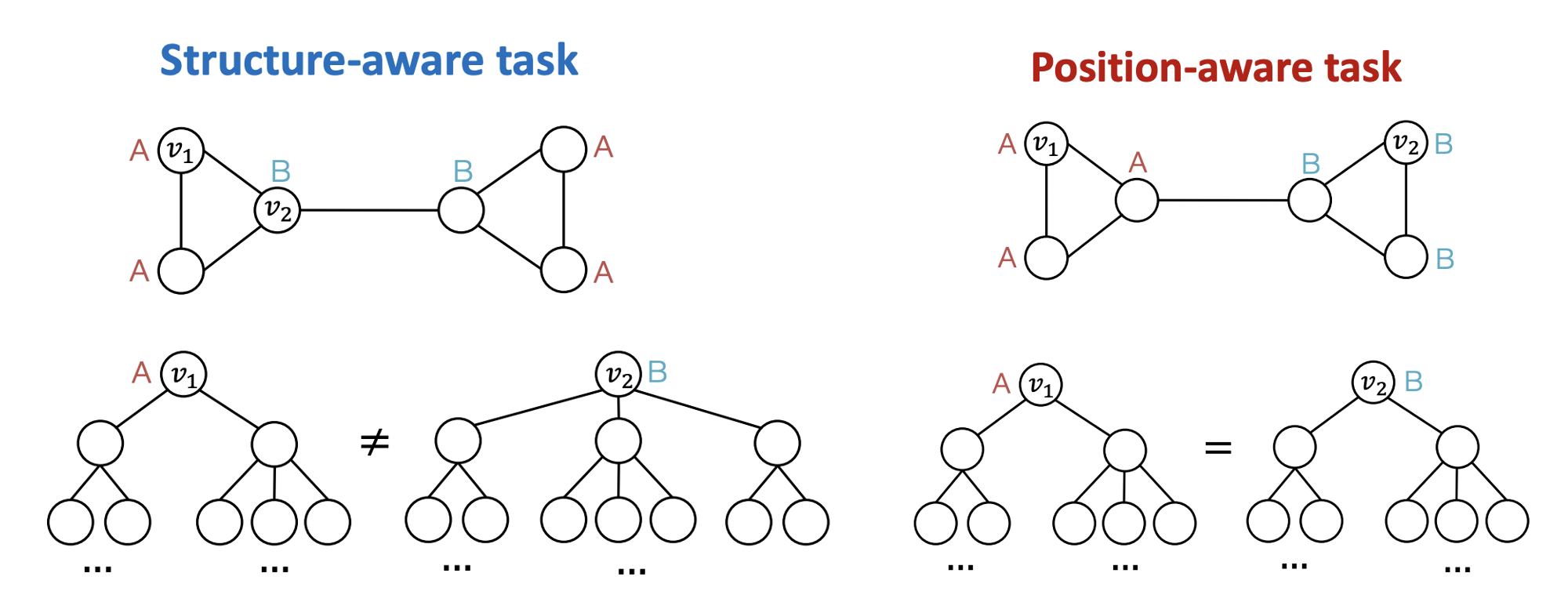
- 노드가 sturucture에 의해 라벨링 될 때 GNN은 서로 다른 computational graph를 만들어 를 구분할 수 있다.
- 노드가 position에 의해 라벨링 될 때 GNN은 과 가 같은 computational graph를 가지도록 만들어 구분을 못한다.
- Position-aware task를 잘 수행하기 위해 anchor를 활용한다.
Powr of "Anchor"
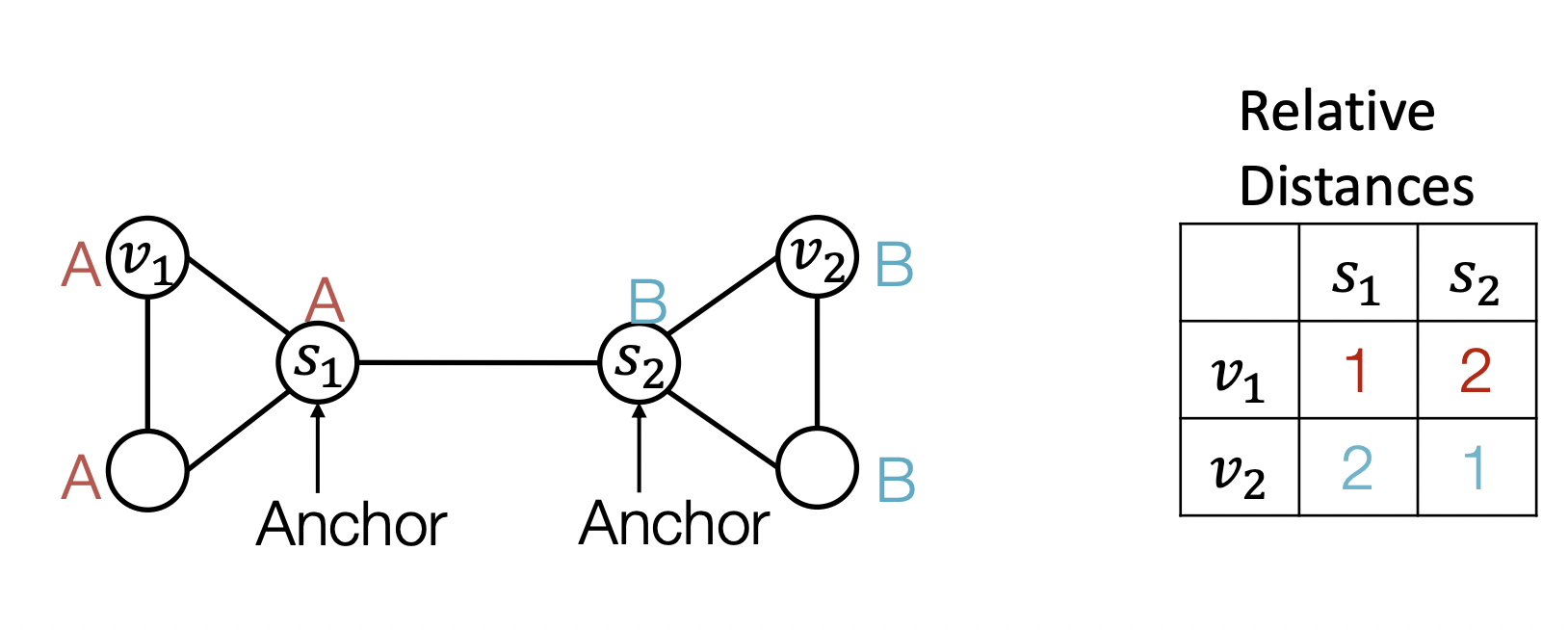
- 임의의 anchor node 을 정한다.
- 에서 까지의 상대적 거리를 나타내 가 좌표축으로써의 역할을 하면 노드의 위치를 알 수 있다.
- Anchor는 많을수록 많은 좌표축이 생기는 것을 의미하므로 더 잘 characterize 할 수 있다.
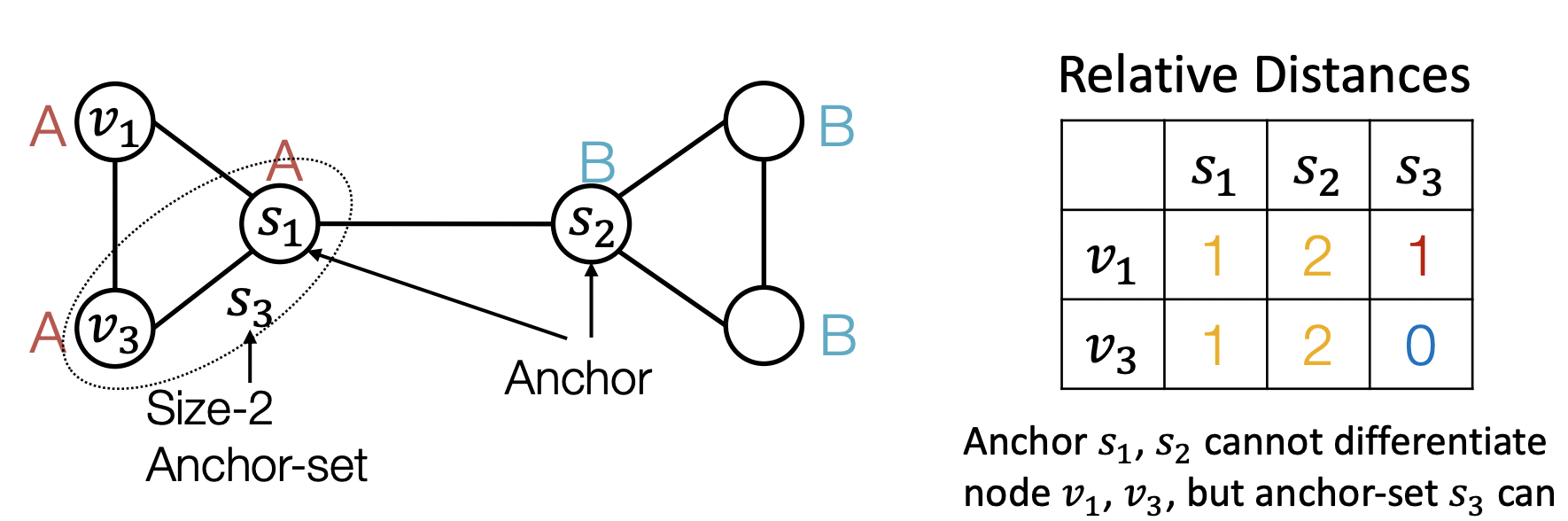
- 여러 노드를 묶어 anchor set으로 활용할 수도 있다.
- Large anchor set은 더 정확한 위치 추정을 도울 수도 있다.
How to Use Position Information
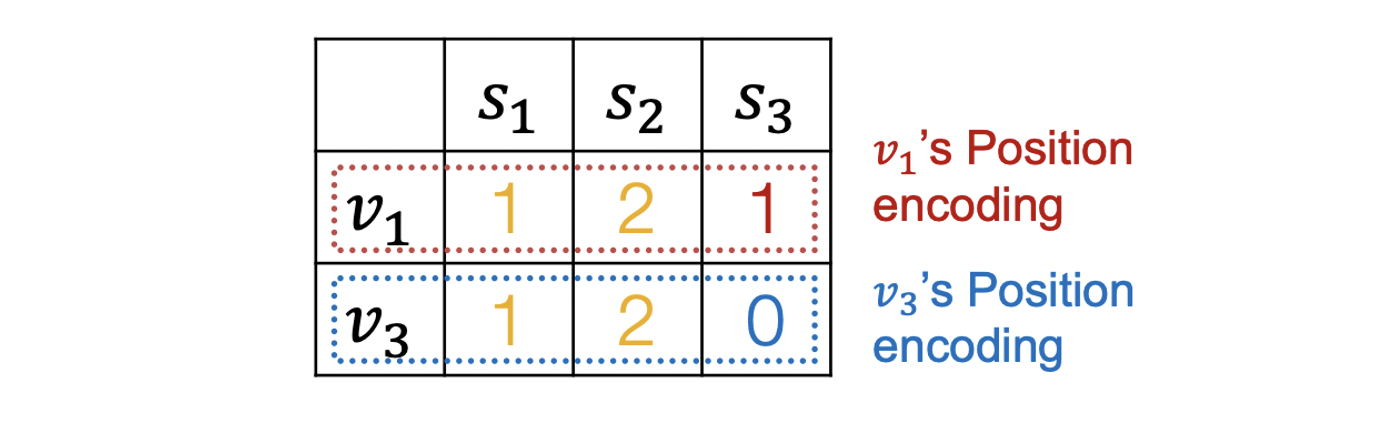
- Anchor를 통해 position을 알면 potision encoding을 augmented node feature로 활용할 수 있다.
- Positioin encoding은 랜덤한 anchor에 따라 차원이 뒤바뀌지만(permutation) 각 차원에서의 값은 그대로이므로 의미가 변하지는 않는다.
3. Identity-Aware Graph Neural Networks
Failure cases of structure-aware tasks
- structure-aware task에서도 GNN의 실패 케이스는 존재한다.
Node-level
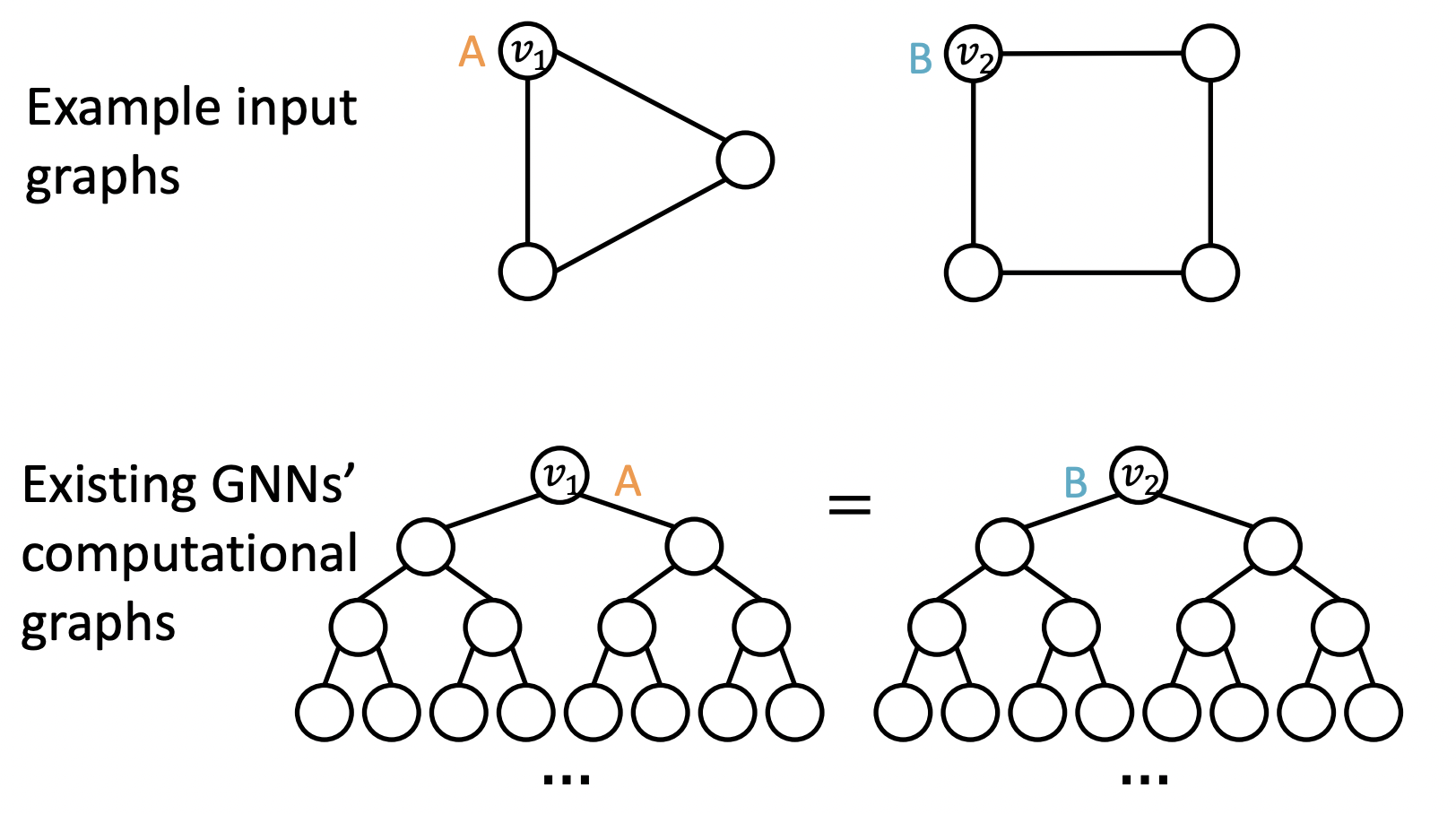
-
과 는 다른 구조를 가지지만 같은 computational graph를 가진다.
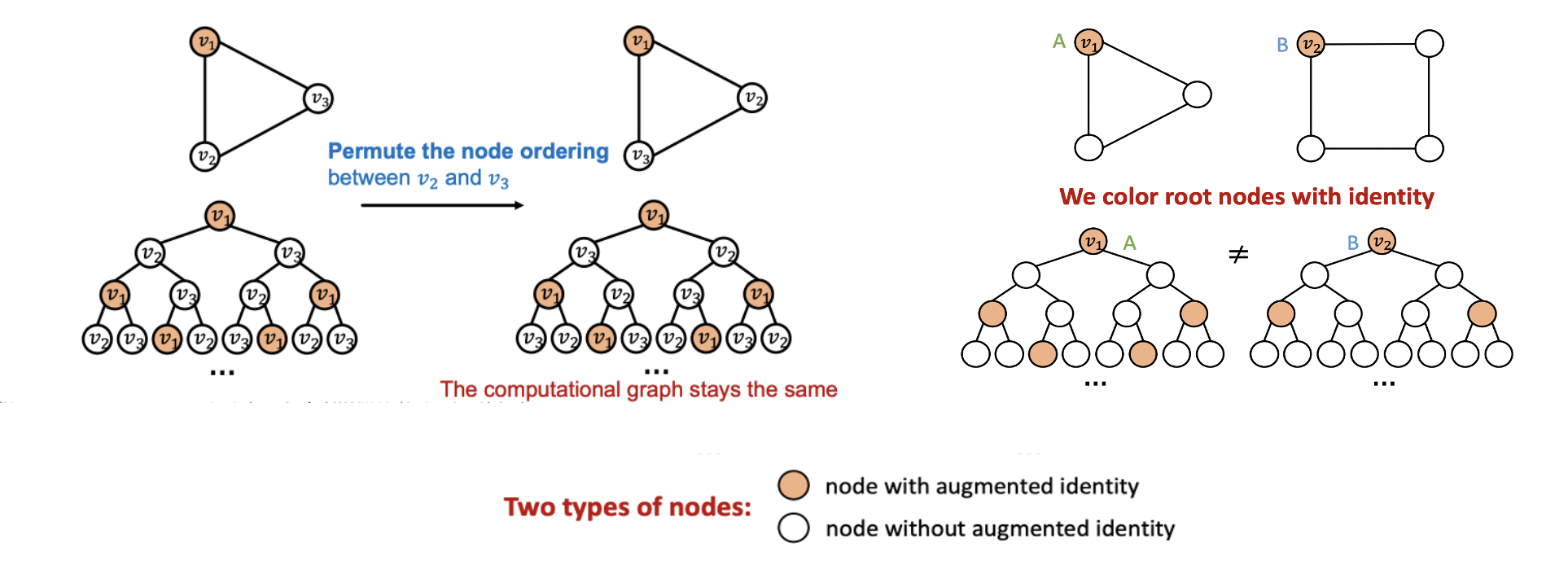
-
임베딩 하고 싶은 노드에 색을 지정하여 ordering/identities invariant한 inductive function을 만들 수 있다.
-
같은 구조 상에서 의 순서가 바뀌어도 동일한 임베딩을 가진다. 즉, 일반화 성능에 도움이 된다.
-
다른 구조를 가지는 노드는 다른 computational graph를 만든다.
Edge level
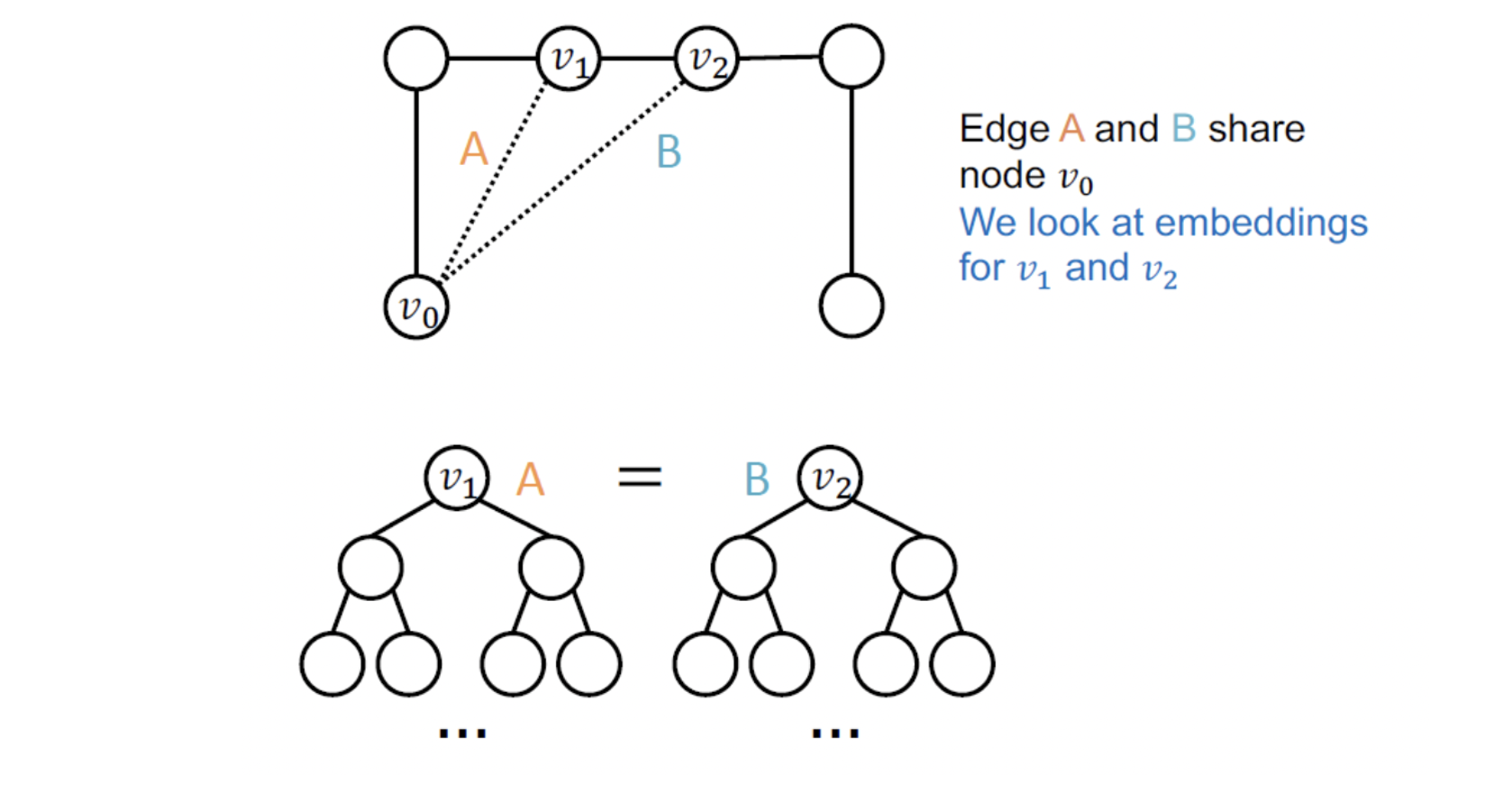
- 가 엣지 를 가지는지에 대한 link prediction을 하는 경우에도 가 같은 임베딩을 가지기 때문에 문제가 생긴다.
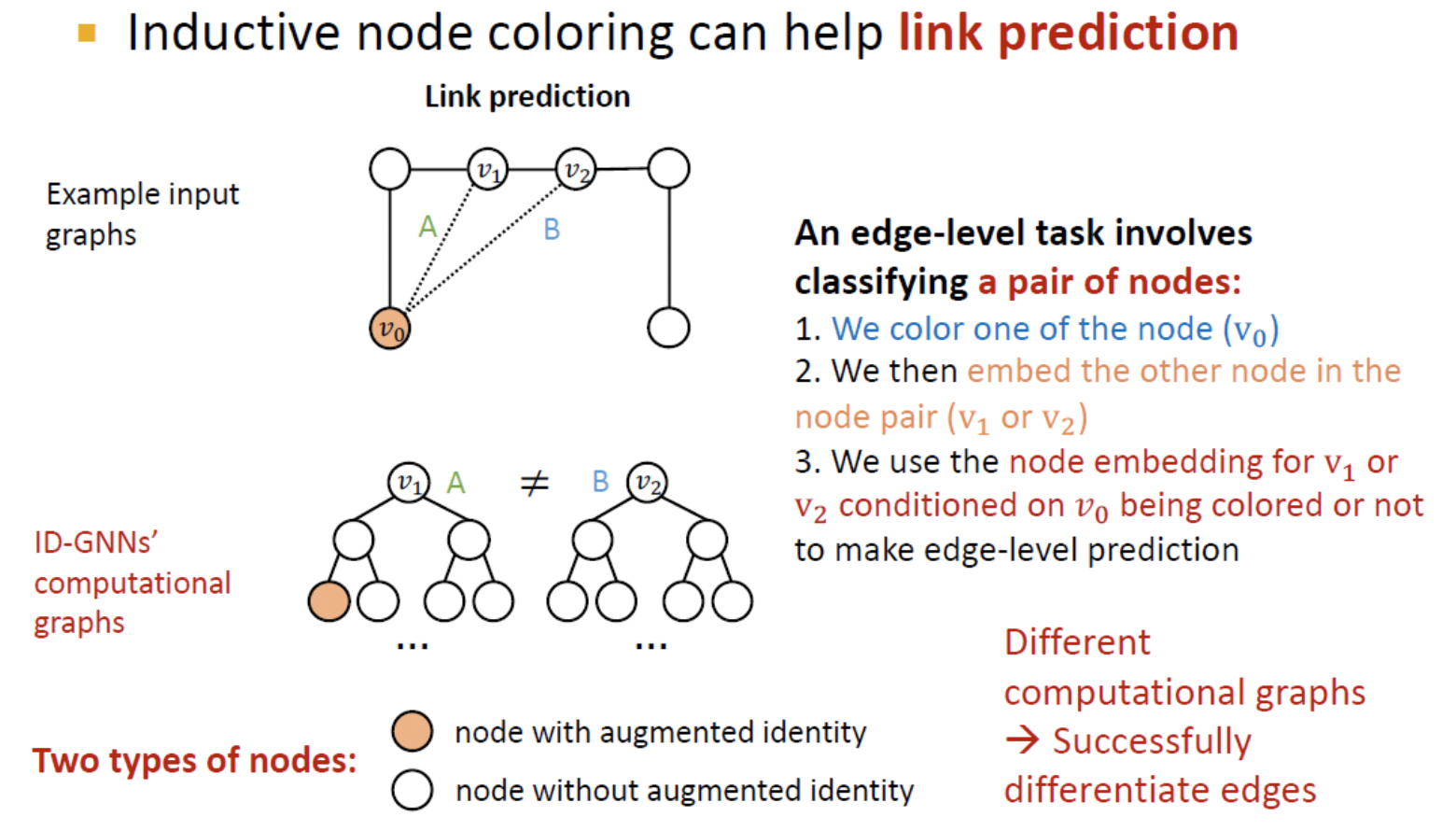
- Coloring을 활용하면 를 구별할 수 있다.
- 와 혹은 와의 노드 쌍이 다른 임베딩을 가지기 때문에 link prediction을 할 때 문제가 없다.
Graph level
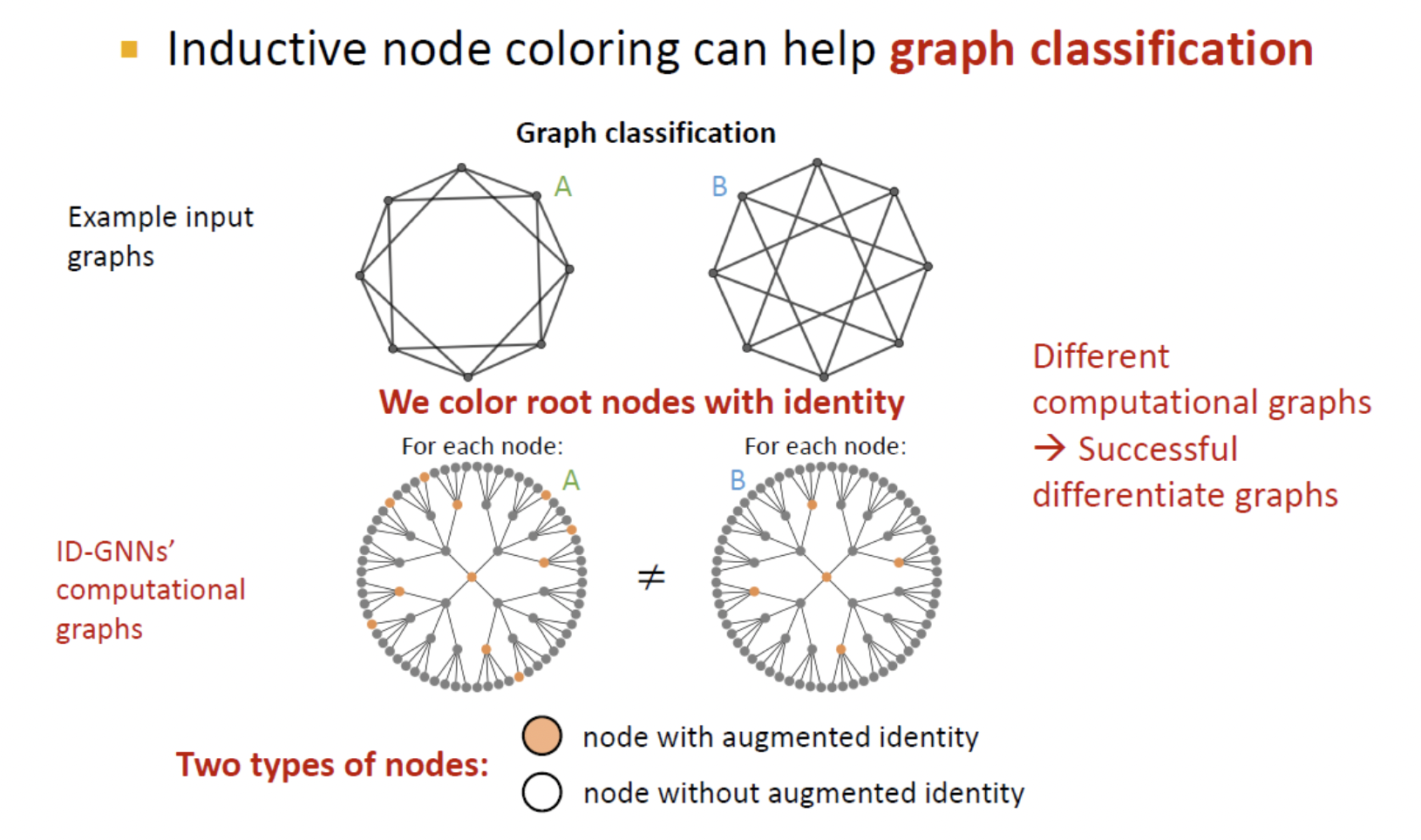
- Graph level에서도 서로 다른 그래프 가 동일한 computational graph를 가진다.
- 마찬가지로 coloring을 통해 구분할 수 있다.
Identity aware GNN
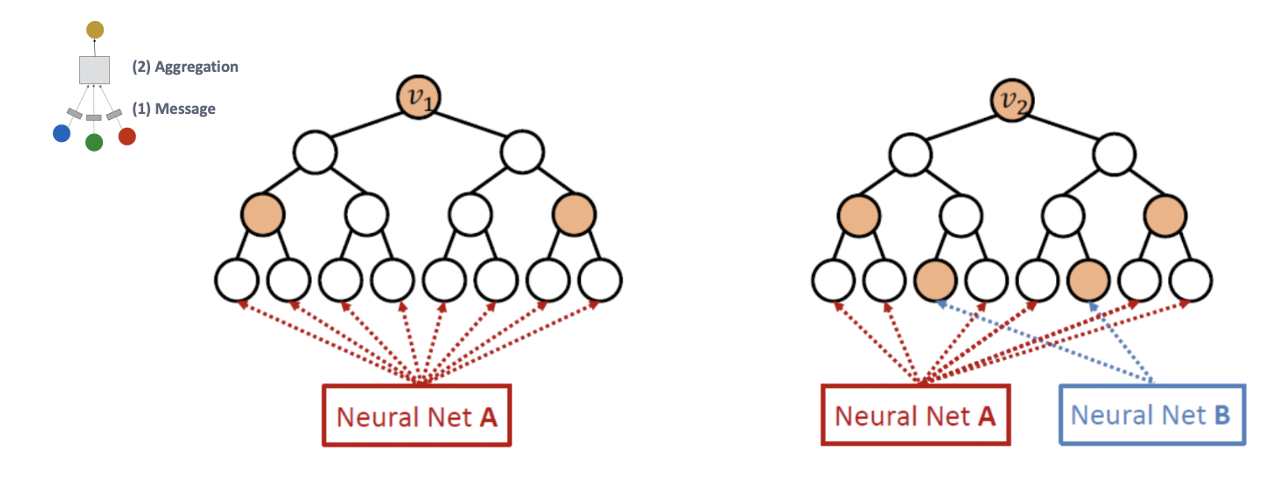
- Coloring을 위해 노드에 따라 다른 network(message/aggregation)를 적용하는 heterogenous message passing을 활용한다.
- 과 는 같은 computational graph를 가지지만 서로 다른 네트워크에 의해 다르게 임베딩 된다.
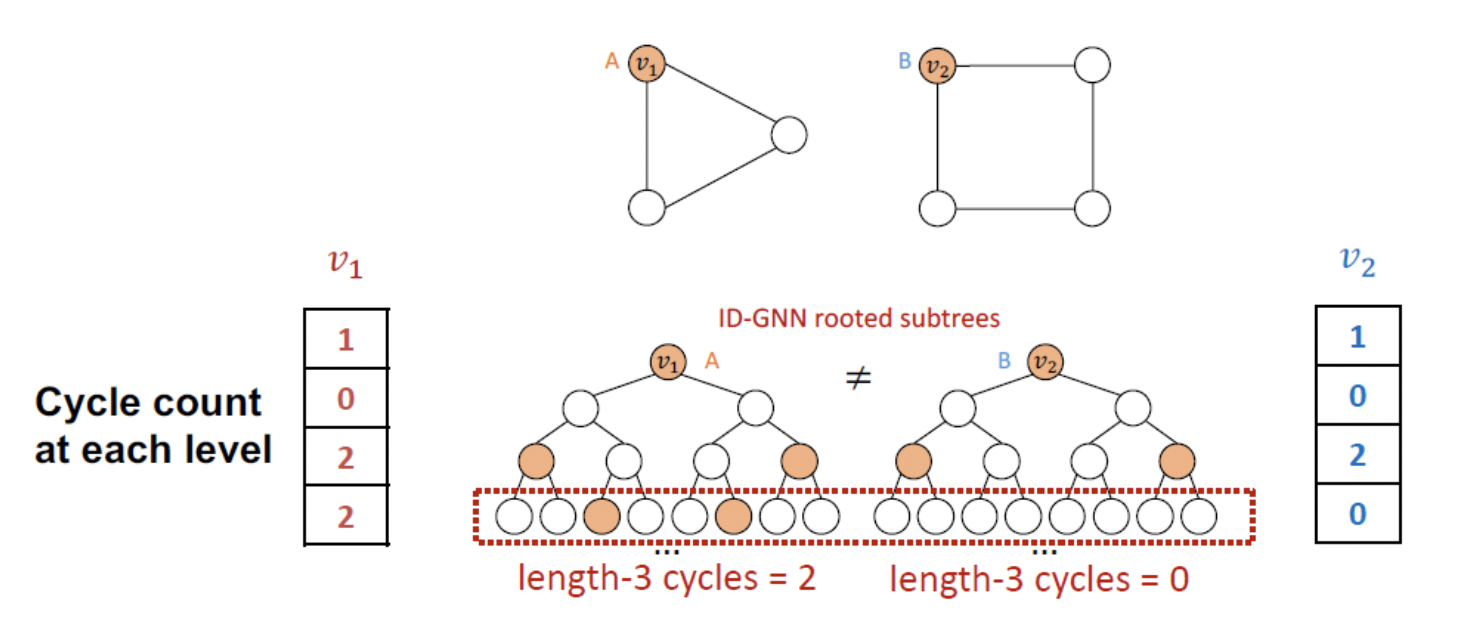
- GNN과 달리 ID-GNN은 cycle count를 계산할 수 있다.
- ID-GNN-Fast에서는 각 레이어에서의 cycle count로 augmented node feature를 heterogenous message passing 없이 간단하게 identity 정보를 가질 수 있다.
4. Robustness of Graph Neural Networks
Robustness
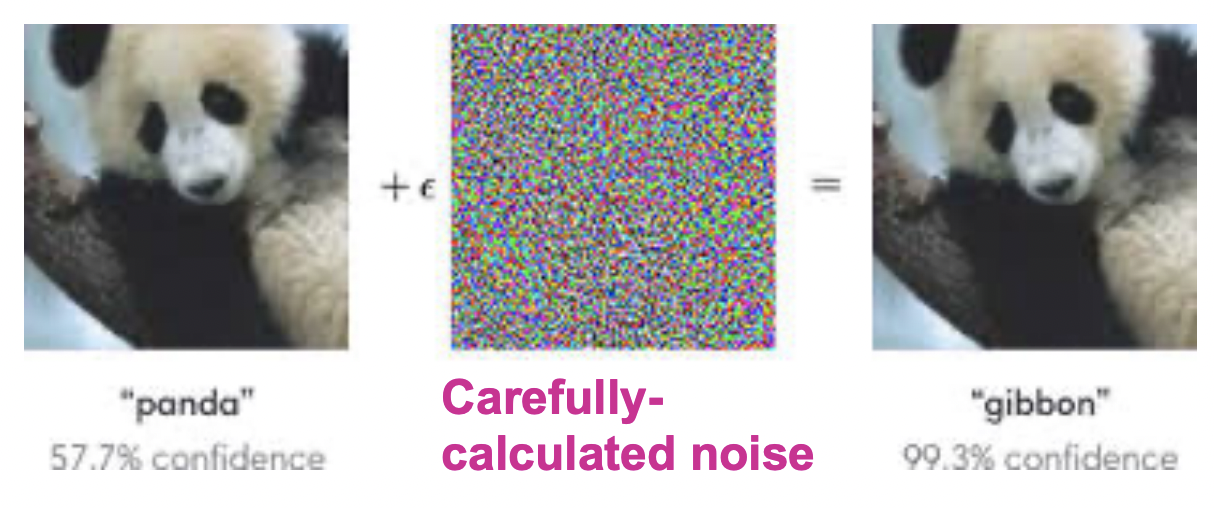
- 딥러닝 네트워크는 adversarial attack에 취약하다.
- 모델이 real world에 적용되기 위해서는 robustness를 갖추는 것이 중요하다.
- input 그래프나 GNN의 prediction이 조작되었을 때 robust해야 하므로 semi-supervised node classification을 한다.
Attack Possibilities
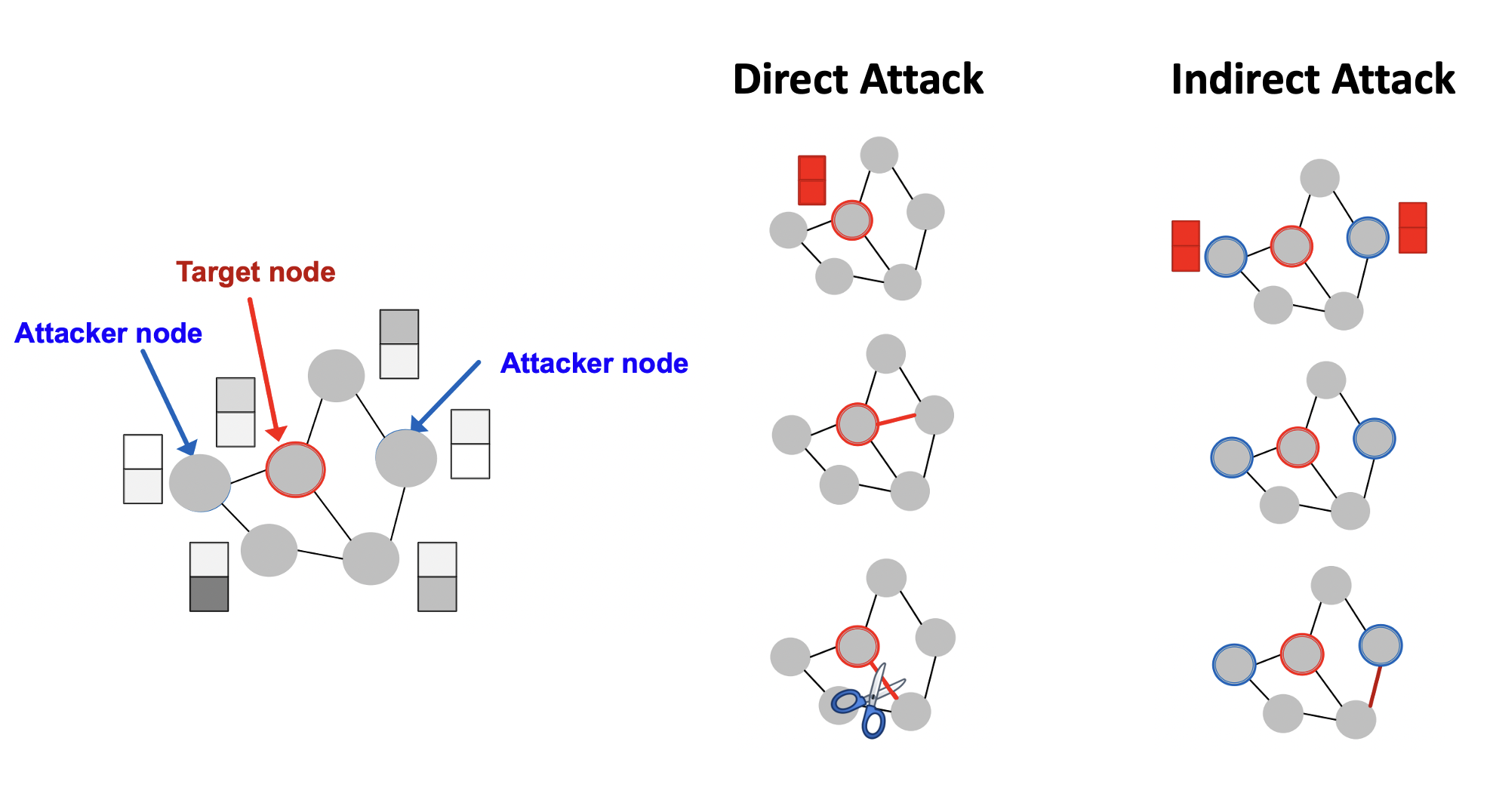
- Target node 는 label prediction을 바꾸고자 하는 노드이다.
- Attacker nodes 는 attacker가 수정할 수 있는 노드이다.
- Direct attack은 로 attacker node가 target node와 동일한 경우이다. 직접 target 노드의 feature를 바꾸거나 엣지를 추가 및 제거할 수 있다.
- Indirect attack 로 target node가 attacker nodes에 속하는 않는 경우이다. Attacker node의 feature 변경 및 엣지의 추가/제거로 target node를 간접적으로 바꾼다.
Mathmatical Formulation
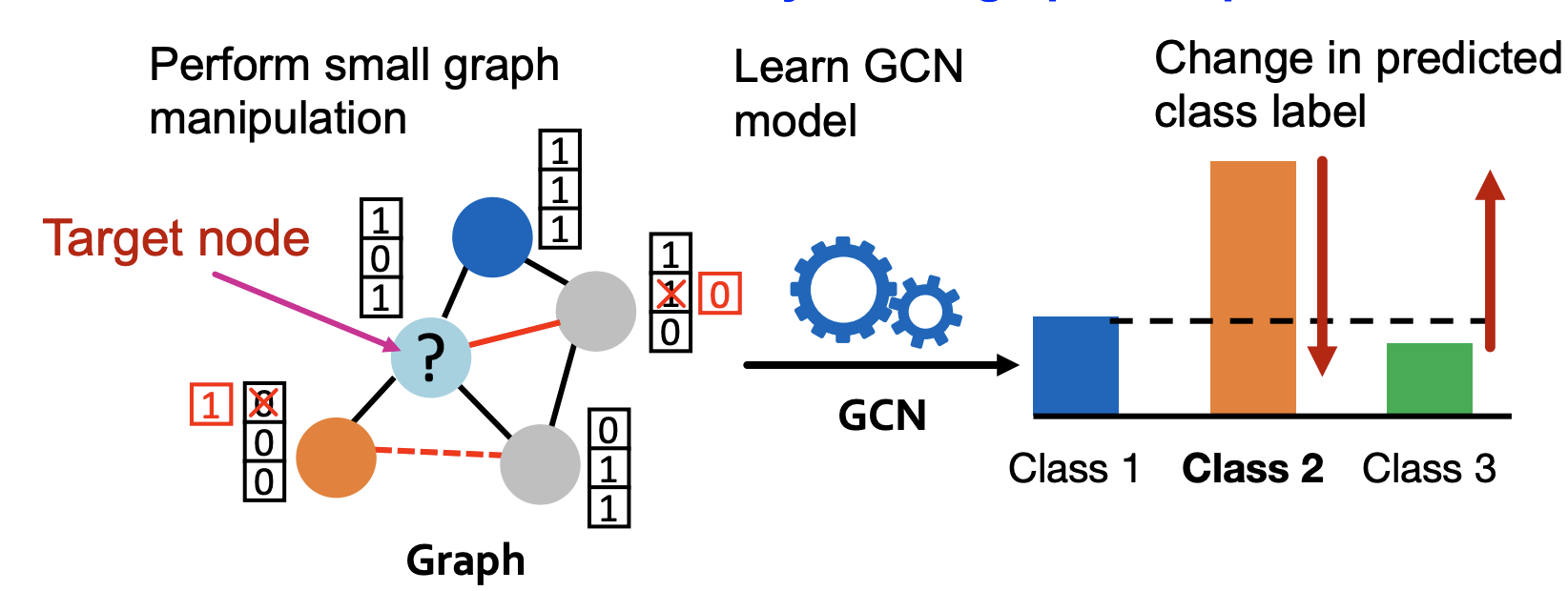
-
Attacker는 조작은 최소화하면서 target node label prediction의 변화는 최대가 되도록 해야 한다.
-
Original 그래프의 인접행렬을 , feature 행렬을 라 하고manipulated 그래프의 행렬들을 이라 하자.

-
GCN은 loss를 최소화하는 를 찾고 target node에 대한 예측 확률이 최대인 클래스를 라 한다.
-
우리는 조작 후의 예측 클래스가 이전의 예측 클래스와 달라지기를 원한다.
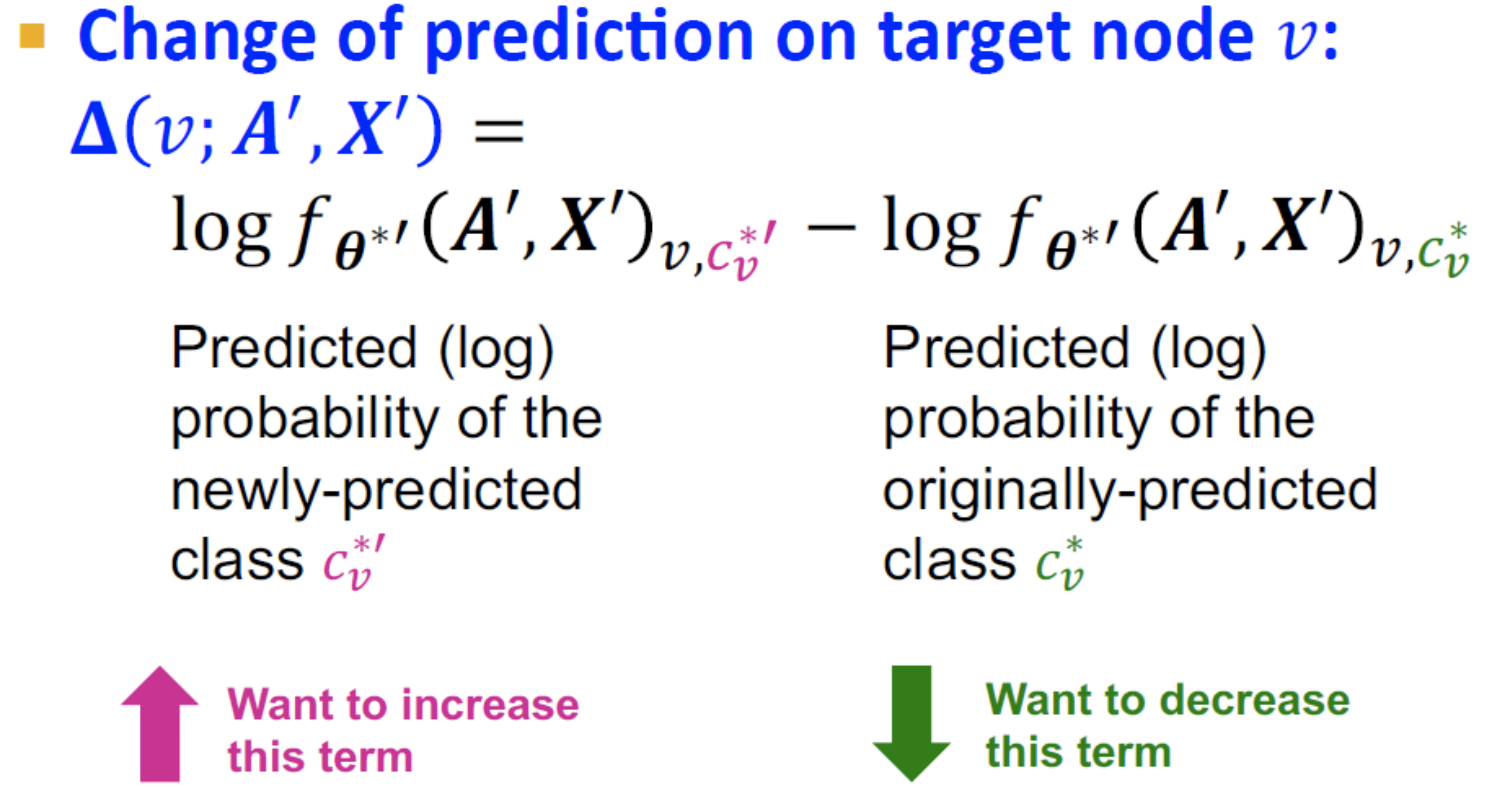
-
새롭게 예측된 의 예측 확률과 기존에 예측되었던 의 확률의 차이가 라는 가정 하에 최대가 되어야 한다.
-
하지만, 인접행렬 가 이산적이기 때문에 gradient를 활용한 최적화가 불가능하고 모든 에 대해 GCN이 retrain 되어야 한다는 문제가 있다.
References
- Lecture 16.1: https://www.youtube.com/watch?v=yT5PziOXxQg&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=49
- Lecture 16.2: https://www.youtube.com/watch?v=6ZFvToZUjGA&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=50
- Lecture 16.3: https://www.youtube.com/watch?v=SJqWQGh__N8&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=51
- Lecture 16.4: https://www.youtube.com/watch?v=uBmtTL3EitI&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=52
