<CS224W> Lecture 8. Applications of Graph Neural Networks

김경준·2022년 4월 5일

CS224W Graph study

CS224W

목록 보기

8/17

1. Graph Augmentation for GNNs

현재까지는 input 그래프가 계산 그래프와 동일하다는 가정이 있었으나 아래와 같은 이유로 부분 그래프를 계산 그래프로 쓸 필요가 있다.
1. Input 그래프는 feature가 부족하여 augmentation 할 필요가 있다.
2. 그래프가 sparse 할 경우 가상의 노드나 엣지를 추가하여 messag를 전달한 이웃노드를 늘릴 수 있다.
3. 그래프가 너무 dense 할 경우 샘플링을 통해 연산량을 줄일 수 있다.
4. 그래프의 크기가 너무 커 GPU에 올릴 수 없는 경우 부분 그래프를 샘플링 할 수 있다.

Feature Augmentation

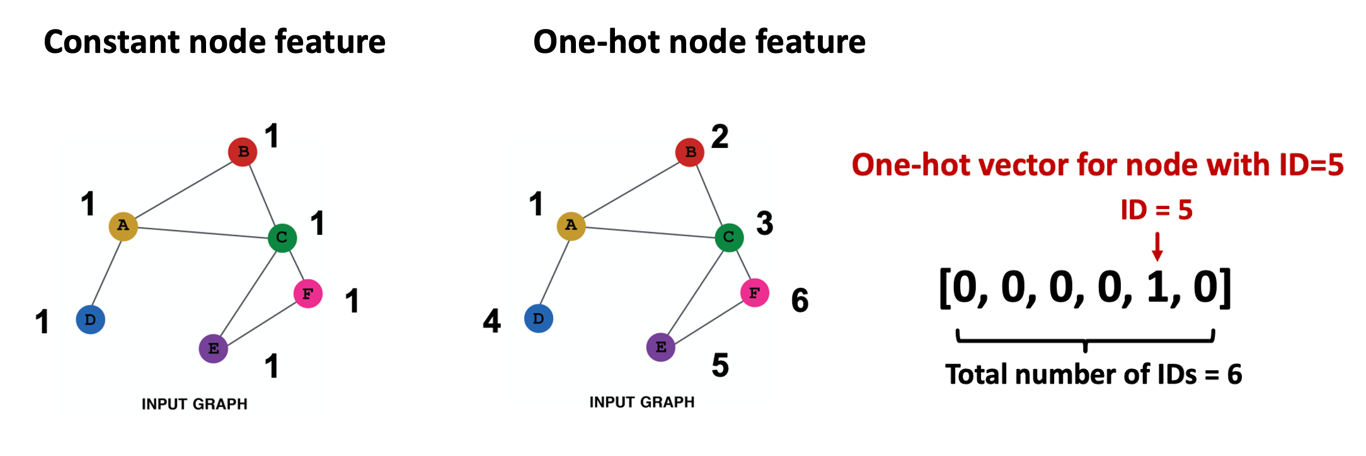
인접행렬만을 가지고 있어 feature가 없는 경우

각 노드에 상수를 부여하거나 one-hot 형태의 ID를 부여할 수 있다.
Constant node feature은 1차원이기 때문에 연산량이 적지만 표현력 또한 그만큼 제한적이다. 또한, 그래프의 크기와 무관하게 적용 가능하며 새로운 노드도 쉽게 일반화할 수 있다.
One-hot node feature은 연산량은 크지만 표현력이 뛰어나며 작은 그래프에만 적용가능하고 새로운 노드는 임베딩할 수 없다.

GNN으로 학습이 어려운 구조인 경우

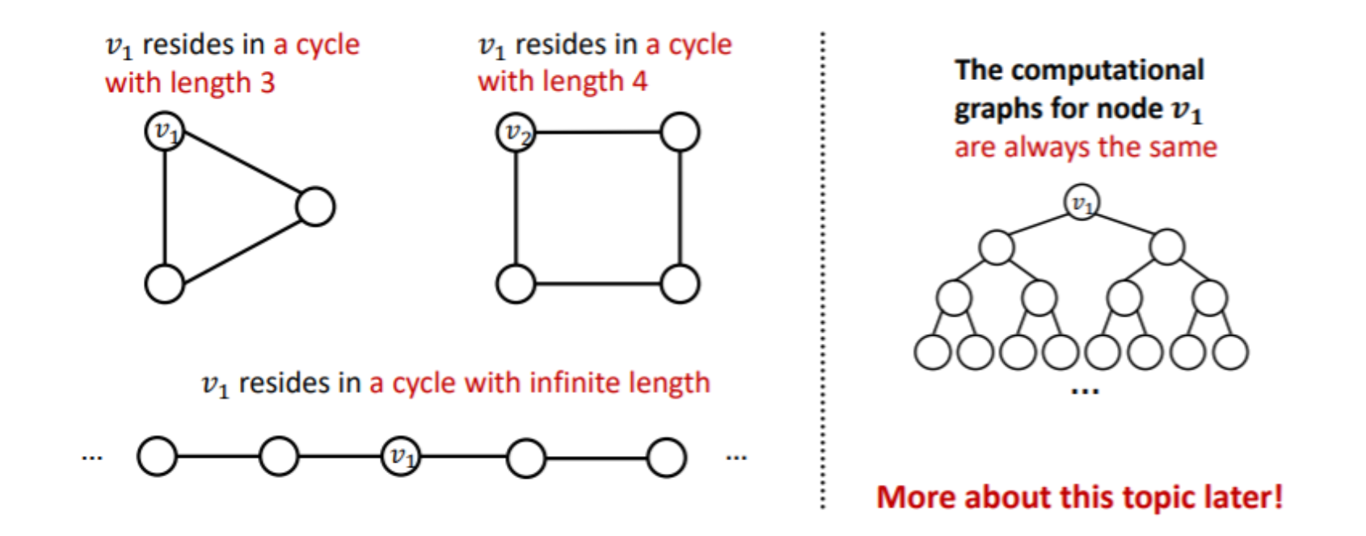
Circle 구조의 그래프의 경우 노드의 갯수가 달라도 모든 노드가 degree=2로 이루어져 있어 계산 그래프가 binary tree 형태가 되기 때문에 두 그래프가 구분이 되지 않는다.
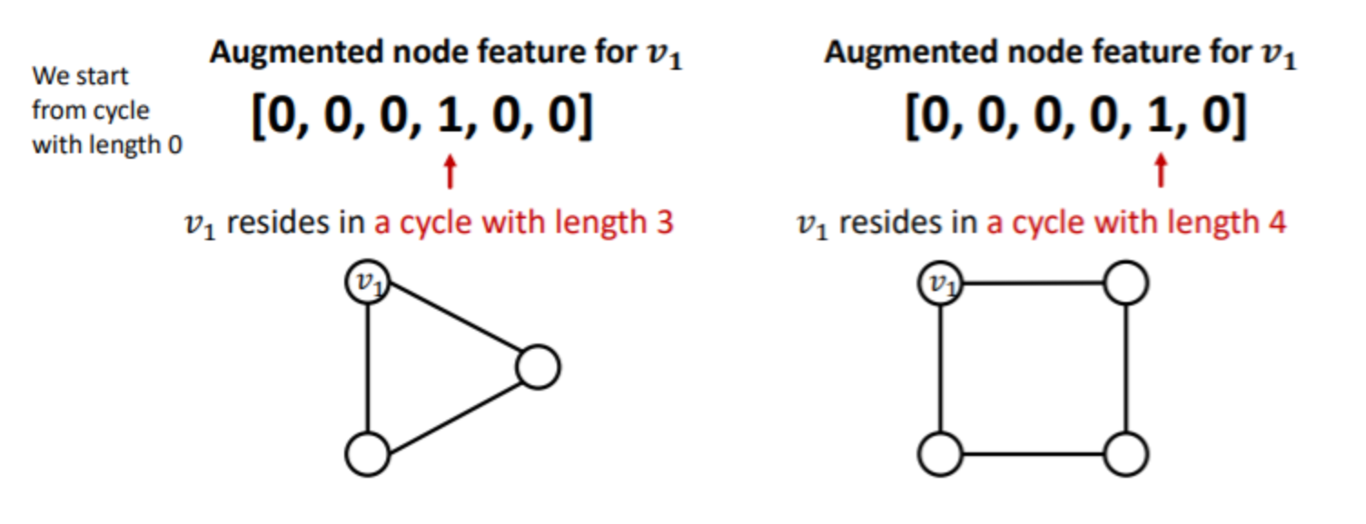
Cycle의 노드의 갯수를 명시하는 등의 방법으로 문제를 해결할 수 있다.

Add Virtual Nodes/Edges

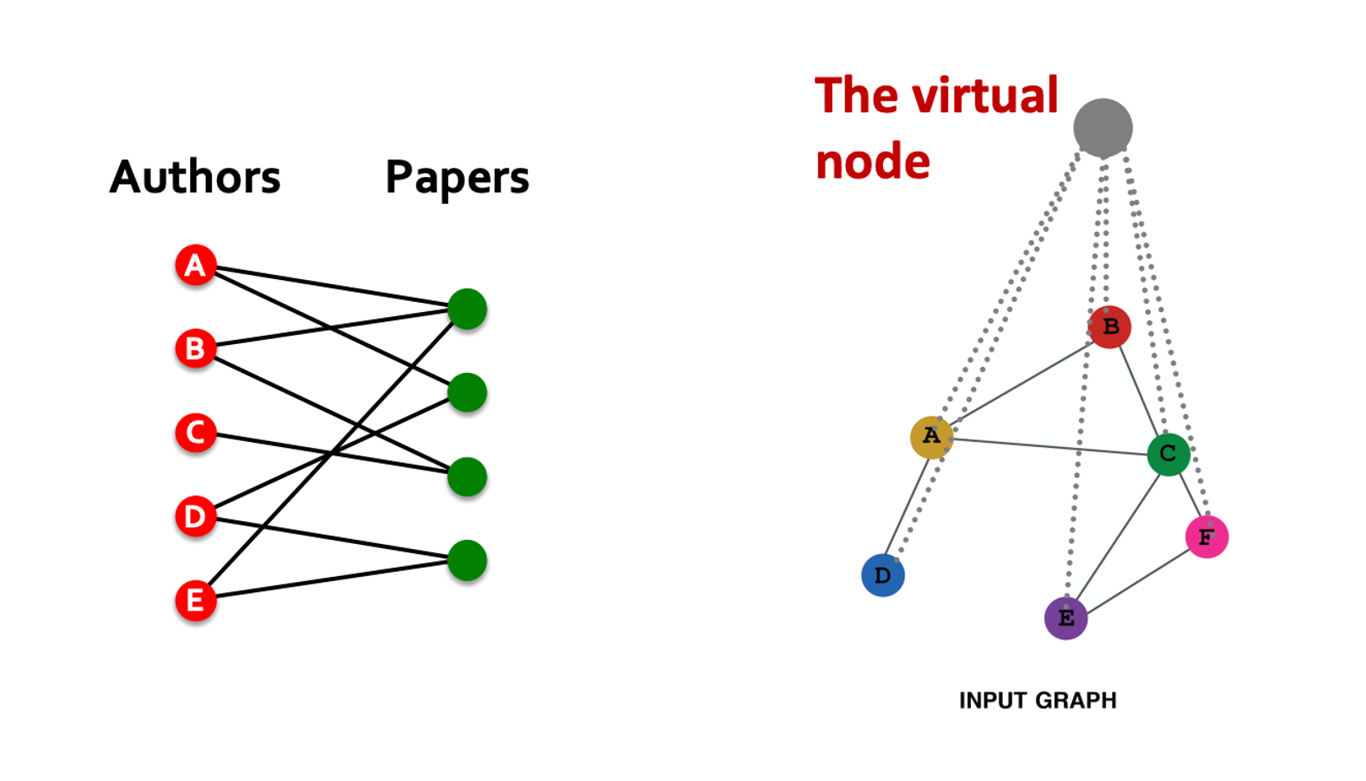
그래프가 sparse한 경우 가상의 엣지 혹은 노드를 추가해줄 수 있다.
인접행렬의 n승은 n-hop으로 갈 수 있는 노드를 나타내므로 GNN의 입력으로 $A+A^2$ 을 이용하면 가상의 2-hop edge를 추가하는 것이 된다.
Bipartite graph에서 2-hop은 같은 집단 내 연결을 의미하므로 효과적으로 활용할 수 있다(ex.authors의 2-hop은 공동저자를 의미)
모든 노드와 연결된 가상의 노드를 만들면 모든 노드가 2-hop으로 연결되어 sparse graph의 문제를 해결할 수 있다.

Node Neighborhood Sampling

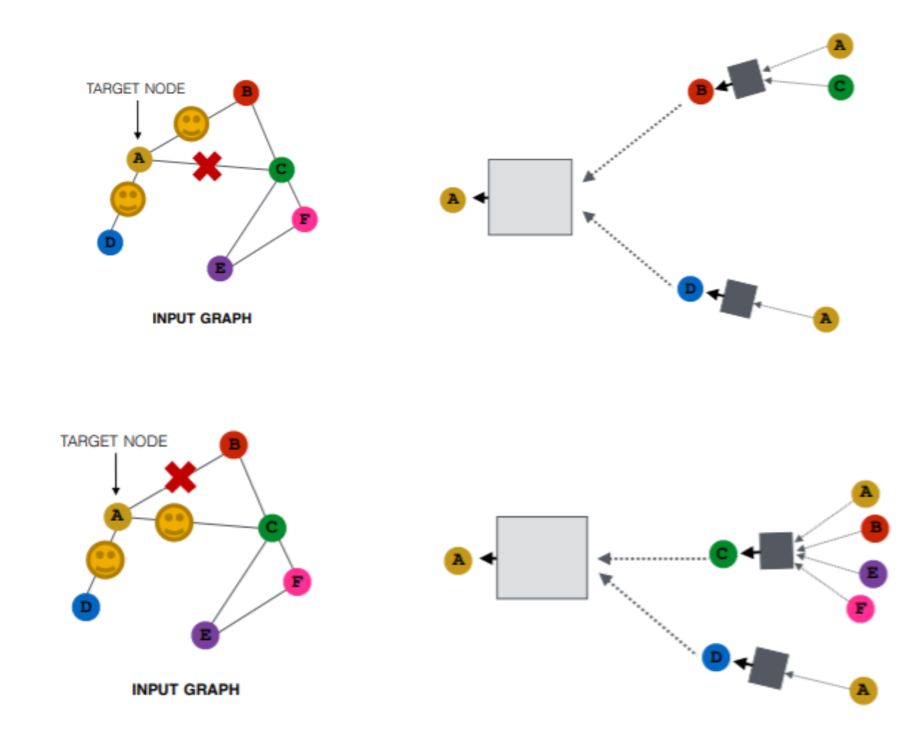
그래프가 너무 dense하여 연산량이 많을 경우 샘플링을 통해 일부 이웃노드만 사용할 수 있다.
매 에폭, 스텝, 레이어마다 샘플링을 고정하지 않고 다르게 반복하여 서로 다른 계산 그래프들로부터 노드 임베딩을 형성할 수 있다.

2. Prediction with GNNs

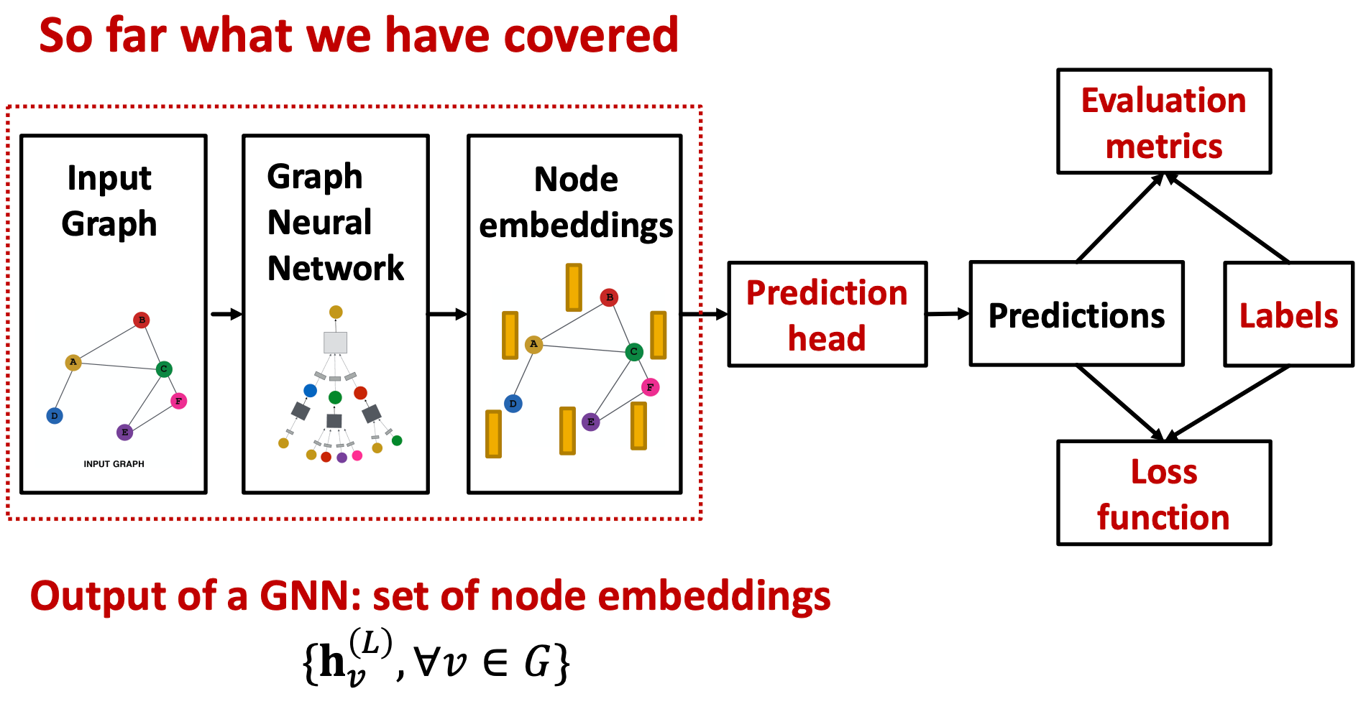
지금까지 다룬 것은 GNN을 통해 노드 임베딩을 형성하는 부분이었다.
같은 GNN 구조를 사용하더라도 task, loss function의 설정에 따라 다르게 학습되며 크게 아래의 세 task로 나눌 수 있다.
1. Node-level tasks
2. Edge-level tasks
3. Graph-level tasks

Node-level tasks

GNN을 거친 $d$ 차원의 노드 임베딩은 다음과 같이 표현할 수 있다.
$\{h_v^{(L)} \in \mathbb{R}^d, \forall v \in G\}$
분류 혹은 회귀의 task를 수행할 수 있으며 GNN의 마지막 레이어의 출력을 head layer에 통과시켜 결과를 얻는다.
$\hat{y}_{v}=H e a d_{n o d e}\left(h_{v}^{(L)}\right)=W^{(H)} h_{v}^{(L)}$

Edge-level tasks

Edge-level task에서는 두 노드의 임베딩 벡터를 head의 입력으로 활용한다.
$\hat{y}_{u v}=H e a d_{e d g e}\left(h_{v}^{(L)}, h_{u}^{(L)}\right)$
Head의 구성으로는 concat 후 선형변환이 있을 수 있다.
$y_{uv}=Linear(Concat(h_u^{(L)},h_v^{(L)})$
Undirected graph의 경우 두 노드의 순서와 무관하게 같은 결과값이 나와야 한다는 점에서 위의 방식은 문제가 있기 때문에 내적을 활용할 수도 있다.
$\hat{y}_{uv}=(h_v^{(L)})^{\top}h_v^{(L)}$
multi-head attention과 유사하게 구성하여 학습 가능한 파라미터 $W$ 를 둘 수도 있다.

$\begin{gathered} \widehat{y}_{u v}^{(1)}=\left(\mathbf{h}_{u}^{(L)}\right)^{T} \mathbf{W}^{(1)} \mathbf{h}_{v}^{(L)} \\ \widehat{y}_{u v}^{(k)}=\left(\mathbf{h}_{u}^{(L)}\right)^{T} \mathbf{W}^{(k)} \mathbf{h}_{v}^{(L)} \\ \widehat{\boldsymbol{y}}_{u v}=\operatorname{Concat}\left(\widehat{y}_{u v}^{(1)}, \ldots, \widehat{y}_{u v}^{(k)}\right) \in \mathbb{R}^{k} \end{gathered}$

Graph-level tasks

Graph-level의 task 또한 모든 노드를 활용해 예측한다.
$\hat{y}_{G}=H e a d_{\text {graph }}\left(\left\{h_{v}^{(L)} \in \mathbb{R}^{d}, \forall v \in G\right\}\right)$
Head는 노드들의 정보들을 종합하는 역할을 하며 아래와 같은 방법들이 있다.

1. Global Mean Pooling: 모든 노드의 벡터를 element-wise하게 평균. 그래프의 크기가 상이하더라도 그 차이를 무시할 수 있다.
$\widehat{\boldsymbol{y}}_{G}=\operatorname{Mean}\left(\left\{\mathbf{h}_{v}^{(L)} \in \mathbb{R}^{d}, \forall v \in G\right\}\right)$
2. Global Max Pooling: 모든 노드의 벡터를 element-wise하게 최대
$\widehat{\boldsymbol{y}}_{G}=\operatorname{Max}\left(\left\{\mathbf{h}_{v}^{(L)} \in \mathbb{R}^{d}, \forall v \in G\right\}\right)$
3. Global Sum Pooling: 모든 노드의 벡터를 element-wise하게 합. 상이한 그래프의 크기를 반영할 수 있다.

Global Pooling Problems

Global pooling은 큰 그래프에서 정보를 잃는다는 단점이 있다.
예를 들어, $G_1:\{-1,-2,0,1,2\}$ 과 $G_2:\{-10,-20,0,10,20\}$ 는 서로 다른 임베딩을 가지고 있지만 Global sum pooling을 할 경우 둘 다 0이 되어 구분할 수 없게 된다.
이러한 문제는 그래프가 클수록 하나의 노드가 가지는 영향력이 작아져 더 크게 나타날 수 있다.

Hierarchical Pooling

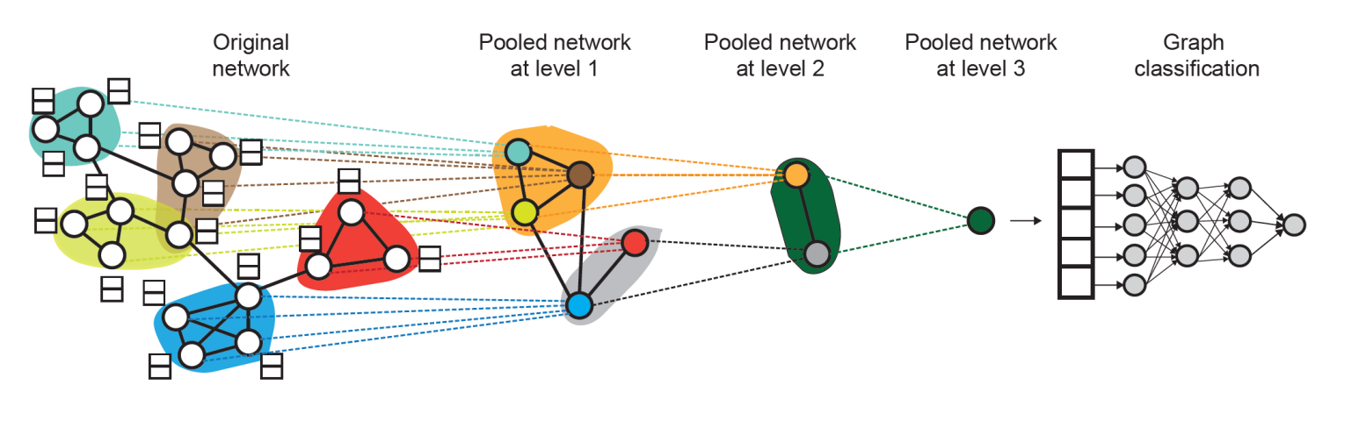
위 문제를 해결하기 위해 계층적으로 풀링하는 방식을 취할 수 있다.
예를 들어, $G_1$ 은
$\hat{y}_a=ReLU(Sum({-1,-2}))=0$
$\hat{y}_b=ReLU(Sum({0,1,2}))=3$
$\hat{y}_G=ReLU(Sum({y_a,y_b}))=3$ 으로 표현할 수 있다.
Subgraph의 임베딩 벡터를 생성하는 GNN과 어떤 노드를 클러스터할지 계산하는 GNN은 각각 독립적으로 작동한다.

3. Training Graph Neural Networks

Labels

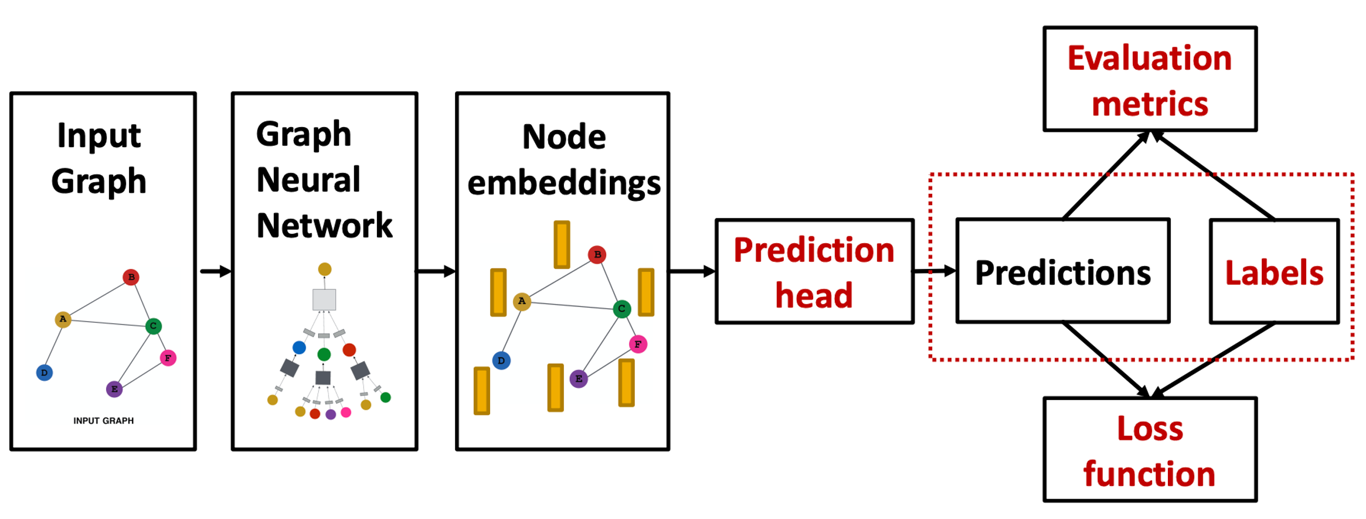
그래프에서 supervised learning은 라벨이 외부 소스로부터 오는 경우(ex.분자구조에 대한 약효 예측 라벨), unsupervised learning은 그래프 내의 정보를 이용하는 경우(ex.두 노드의 엣지 존재 유무)를 의미한다.
Unsupervised learning은 경계가 모호해져 self-supervised learning와 동일시되기도 하며 노드 정보, 엣지 유무 등 그래프 내의 있는 요소 중 지도 학습으로 사용될 수 있는 요소를 찾는 것이 핵심이 된다.

Loss function

Classification: prediction head를 거친 벡터에 softmax를 취해준다.
Regression: 일반적으로 Mean Squared Error(MSE)가 많이 쓰인다.

Evaluation Metrics

Classification: 다중 분류에서는 accuacy가, 이진 분류에서는 accuracy와 함께 precision, recall, f1-score, ROC, AUC도 사용된다.
Regression: RMSE와 MAE가 주로 사용된다.

4. Setting-up GNN Prediction Tasks

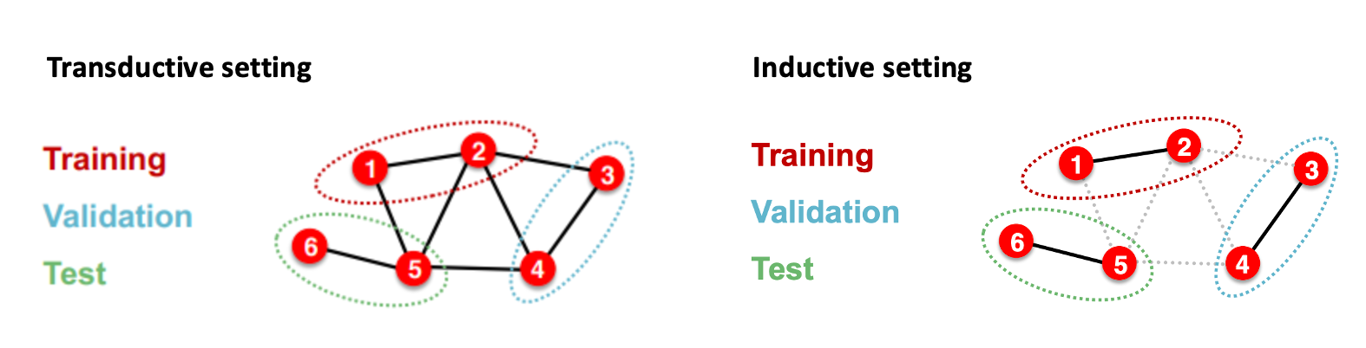
그래프는 이미지, 텍스트와 달리 train, validation, test 데이터로 나눠도 상호종속적이다.
그래프의 데이터셋 분리에는 transductive setting과 inductive setting이 있다.

Transductive setting

Input graph가 모든 data splits에서 활용되며 노드의 라벨만이 나뉜다.
Training 시에는 전체 그래프의 임베딩을 계산하고 노드1,2의 라벨을 활용해 학습한다.
Validation 시에는 전체 그래프의 임베딩을 계산하고 노드3,4의 라벨을 평가한다.

Inductive setting

엣지를 끊어 세 개의 독립적인 그래프를 만든다. 노드5는 더 이상 노드1의 예측에 영향을 미치지 않는다.
Training 시에는 노드1,2만의 임베딩을 계산하며 노드1,2의 라벨을 통해 학습한다.
Validation 시에는 노드3,4의 임베딩을 계산하며 노드3,4의 라벨로 평가를 한다.

Node Classification

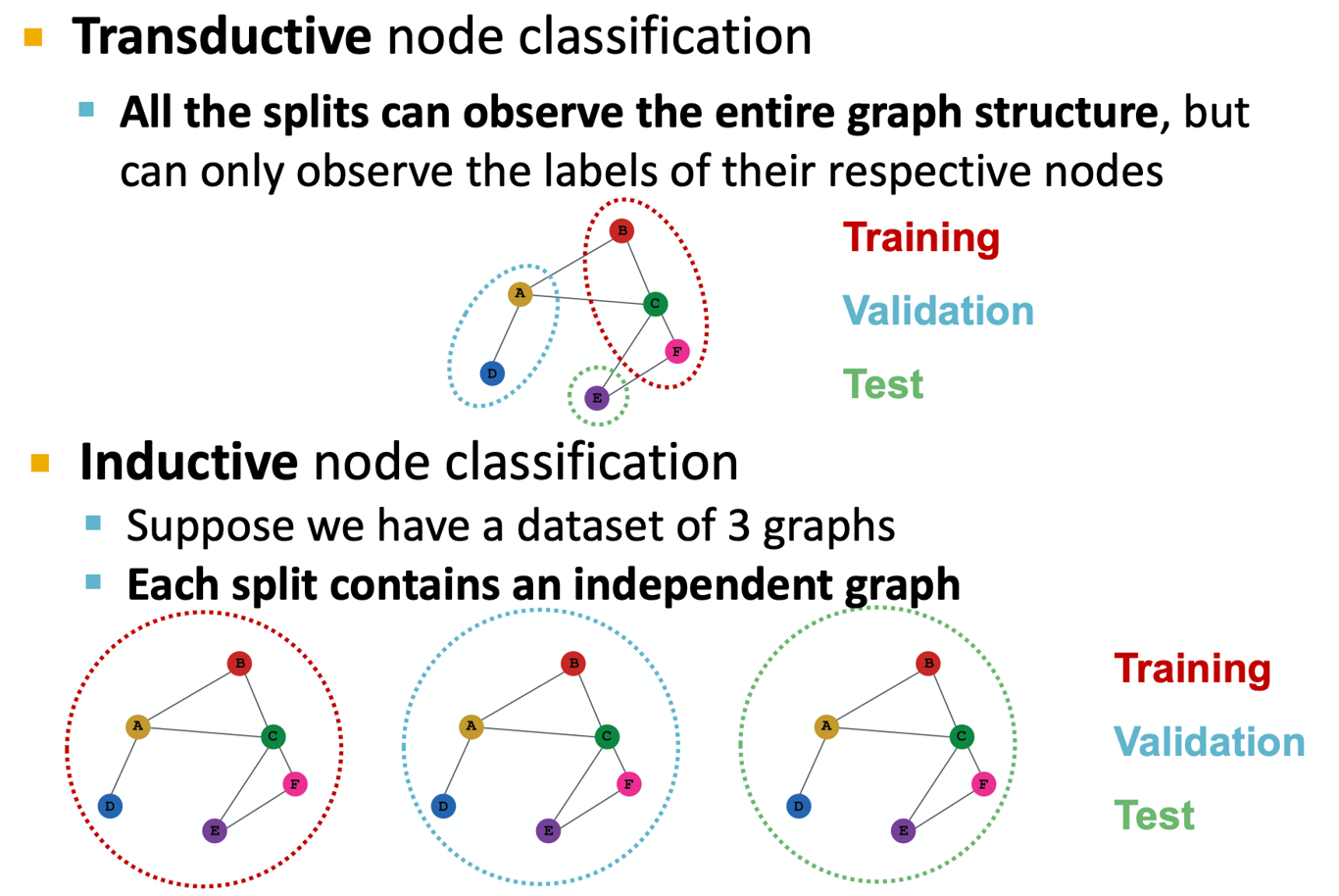
노드의 분류는 transductive, inductive setting가 모두 가능하다.
Transductive setting에서는 모든 split이 그래프를 공유하지만 receptive node의 라벨만을 볼 수 있고 Inductive setting에서는 split마다 독립적인 그래프가 존재한다.

Graph Classification

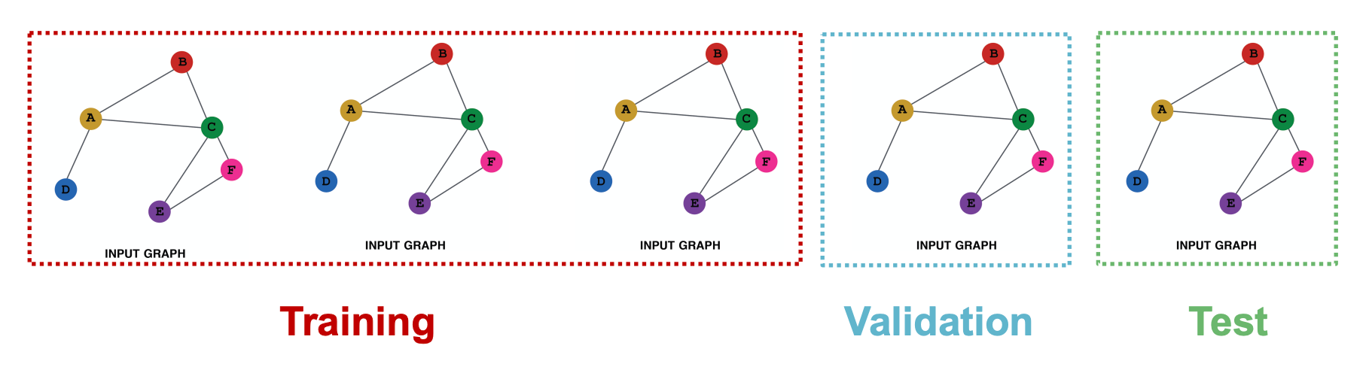
그래프의 분류는 unseen graph에 대해 테스트를 해야하기 때문에 inductive setting에서만 정의된다.
.

Link Prediction

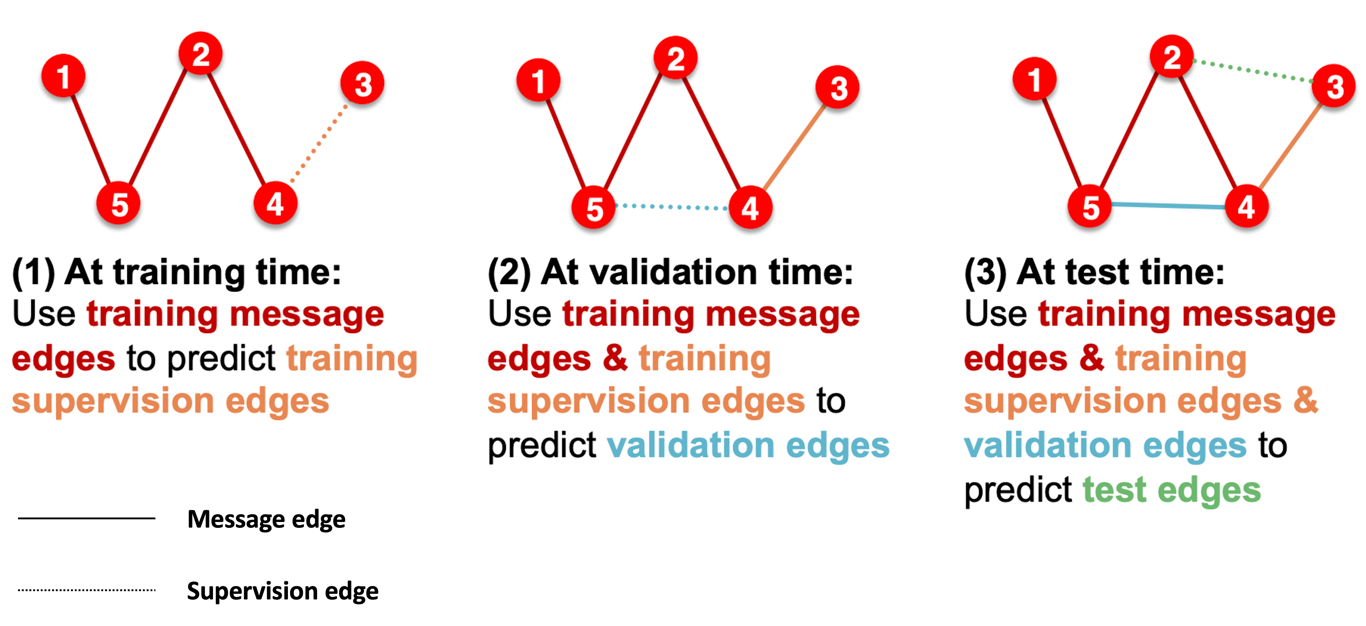
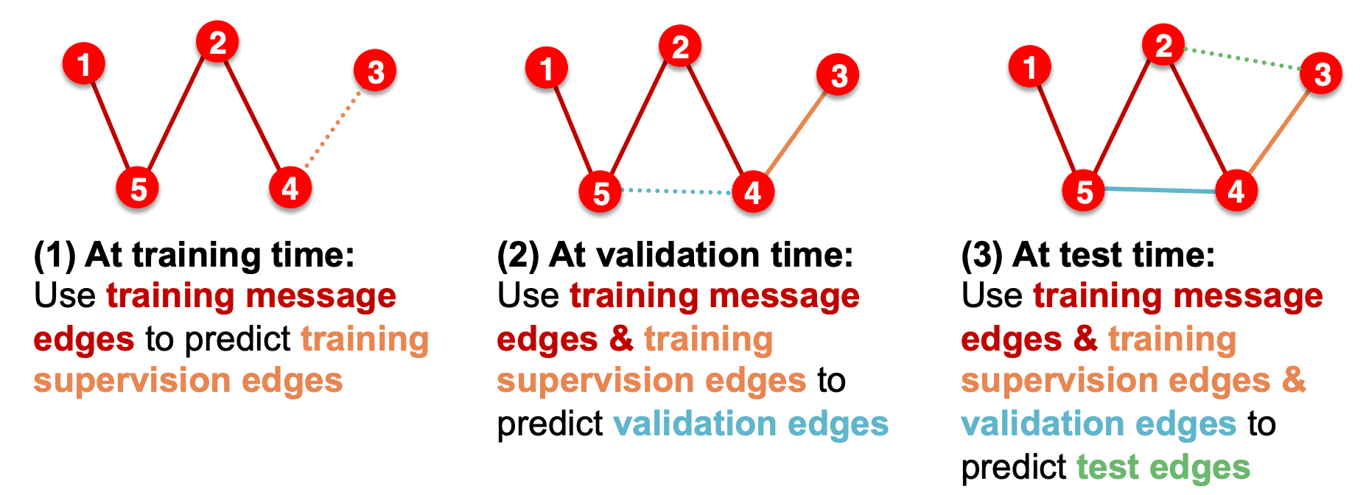
Link prediction은 self-supervised task로 edge를 제거한 뒤 존재여부를 예측하도록 구성한다.
Message passing 시 사용되는 Message edge와 예측을 수행할 supervision edge로 나뉘게 된다
그래프가 하나인 경우 transductive setting으로 supervision edge만 데이터셋에 따라 분리된다. 학습 후 supervision edge는 GNN이 알고있으므로 validation 시에는 message edge로 사용하여 grow하는 방식이 이상적이다.
Inductive setting은 그래프가 여러개인 경우로 각각의 그래프를 split하면 된다.