1. How Expressive are Graph Neural Networks

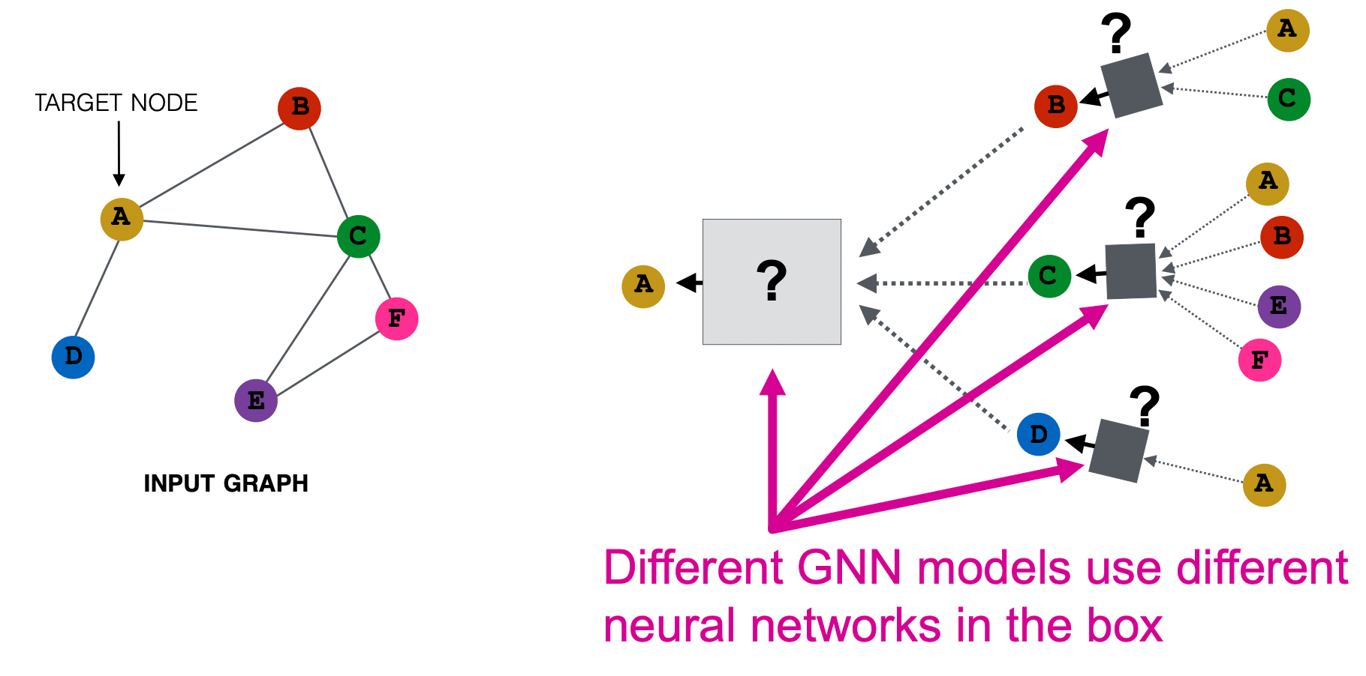
• 우리는 local network neigborhood에 기반하여 노드 임베딩을 생성하고자 한다.

• 이를 위한 다양한 GNN 모델들이 나왔으며 GCN은 element-wise mean pooling+Linear+ReLU를 이용하고 GraphSAGE는 MLP+element-wise max-pooling을 이용하는 등 그 방식이 다양하다.
  

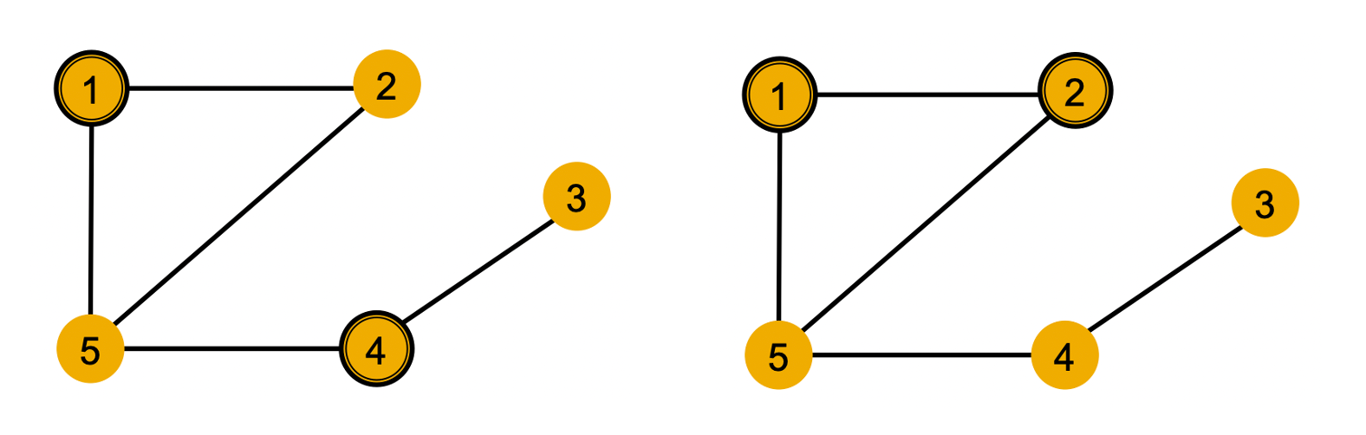
• 노드의 색상이 feature를 나타낸다고 하자. 즉, 같은 색상의 노드는 같은 feature를 가지고 있음을 의미한다.

• 이 때 노드1과 노드4는 이웃 노드의 degree가 달라 구분할 수 있지만 노드1과 노드2는 그래프 상에서 symmetric하여 구분할 수 없다.

Computational Graph

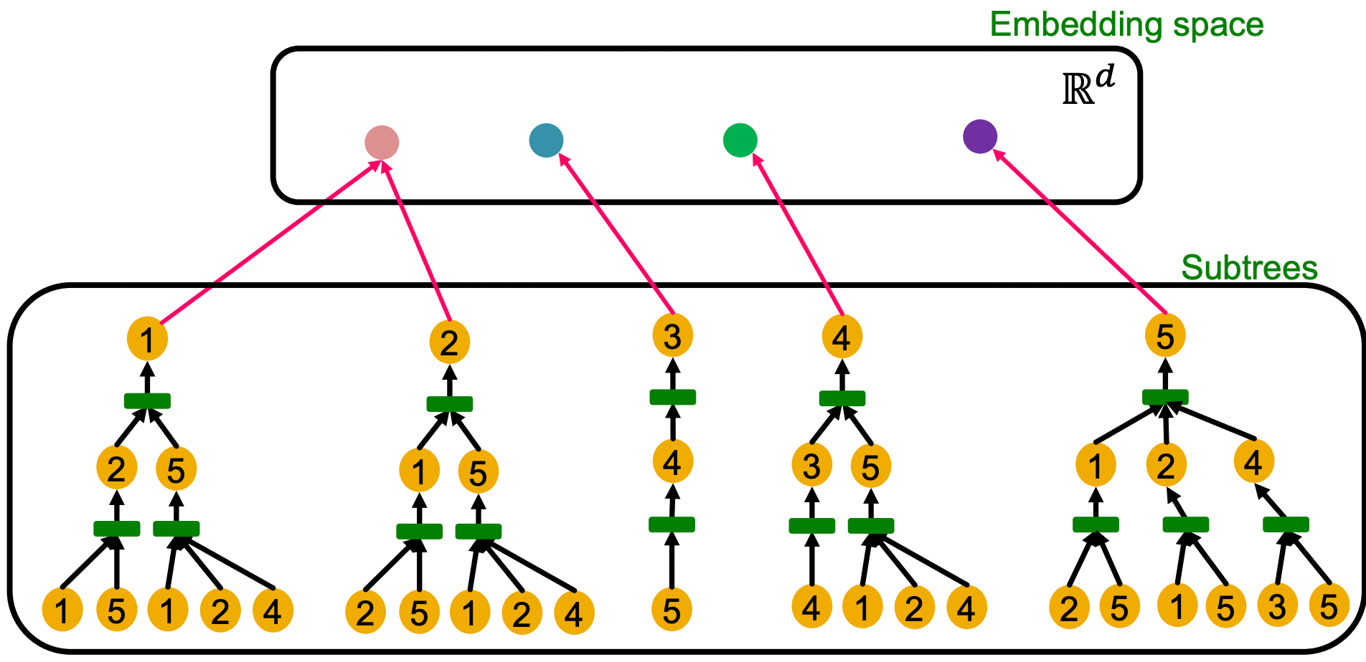
• 각 노드에 대한 subtree를 만들 수 있으며 ID는 고려하지 않으므로 노드1과 2는 embedding space에서 동일한 것이 된다.
• GNN이 효율적이기 위해서는 injective하게 서로 다른 계산 그래프에 대해 각각 다른 임베딩 벡터를 출력하는 함수가 되어야 한다.
  
• 동일한 높이를 가지는 계산 그래프는 leaf node부터 root node까지 반복적으로 정보를 처리하여 구분을 한다.
• 반복적으로 정보를 처리하는 부분이 aggregation function이며 이 함수가 단사함수일 때 표현력이 큰 GNN이 될 수 있다.

2. Designing the Most Powerful Graph Neural Network

Neighbor Aggregation

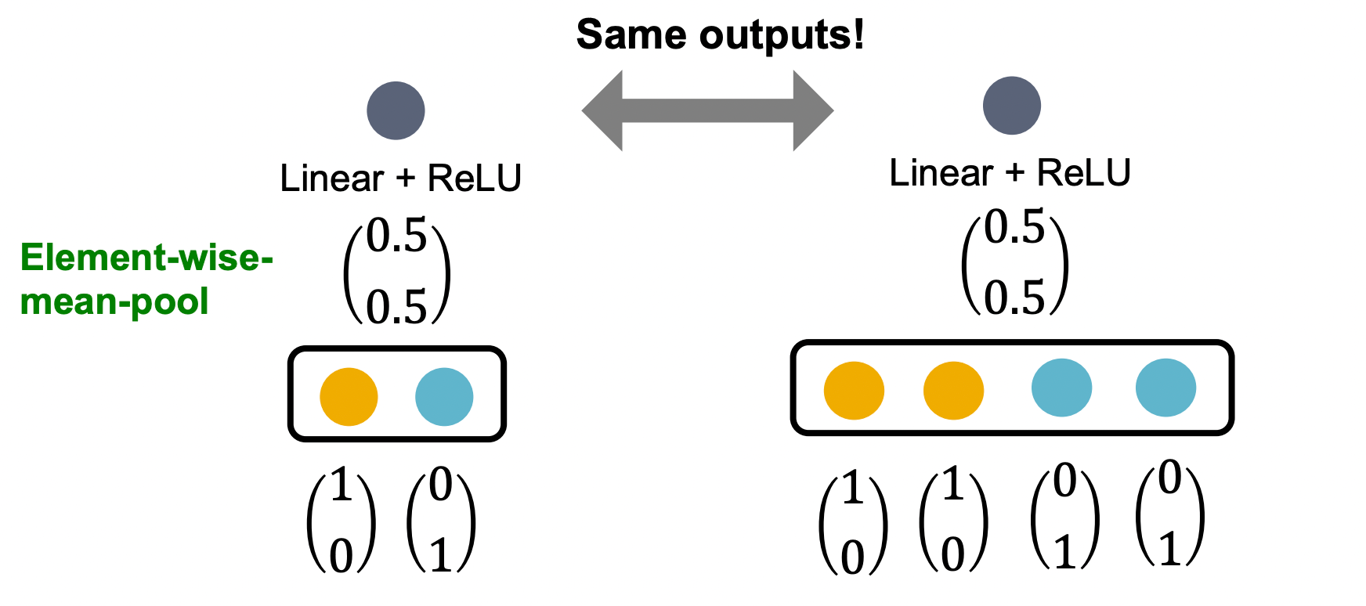
• GCN은 element-wise mean+Linear+ReLU를 통해 aggregationg한다.
• 이러한 방식은 동일한 색상 비율을 가지는 multi-set를 구분하지 못한다.
• 각 노드의 색상이 one-hot encoding으로 표현된다고 할 때 노드의 수가 2배가 되어도 output은 동일한 모습을 보인다.

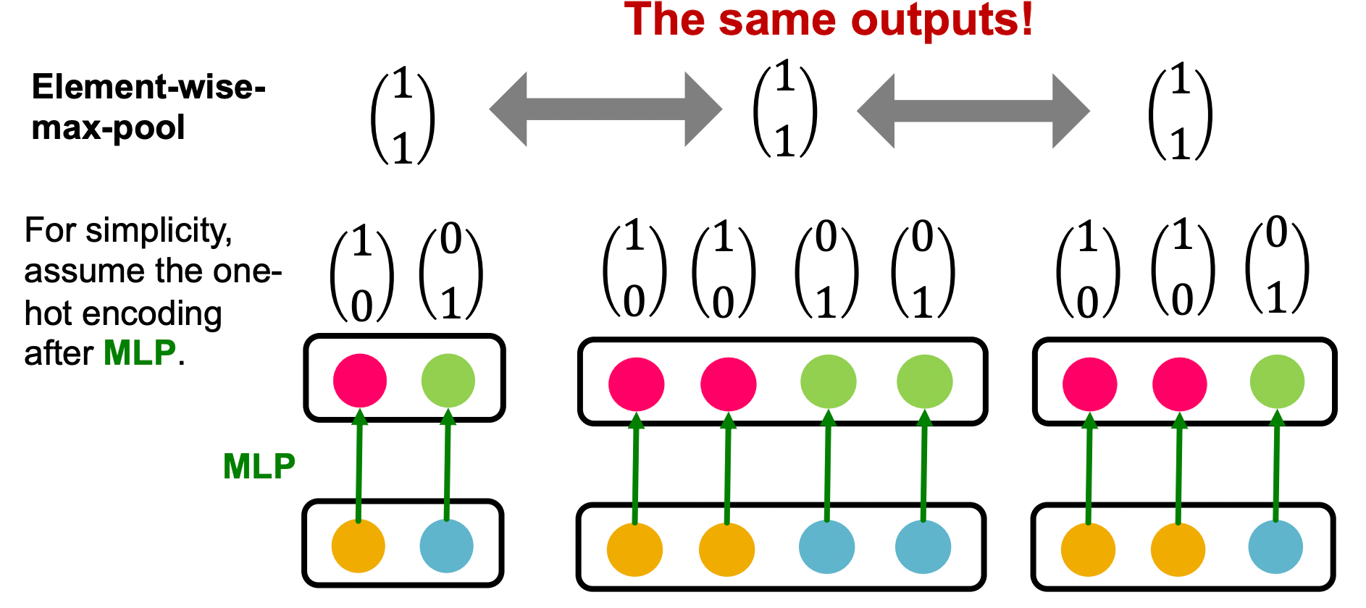
• GraphSAGE는 MLP+element-wise max로 aggregation한다.
• 이러한 방식은 같은 색상의 노드들이 전부 존재한다면 갯수와 무관하게 같은 output을 가지게 된다.

Graph Isomorphism Network(GIN)

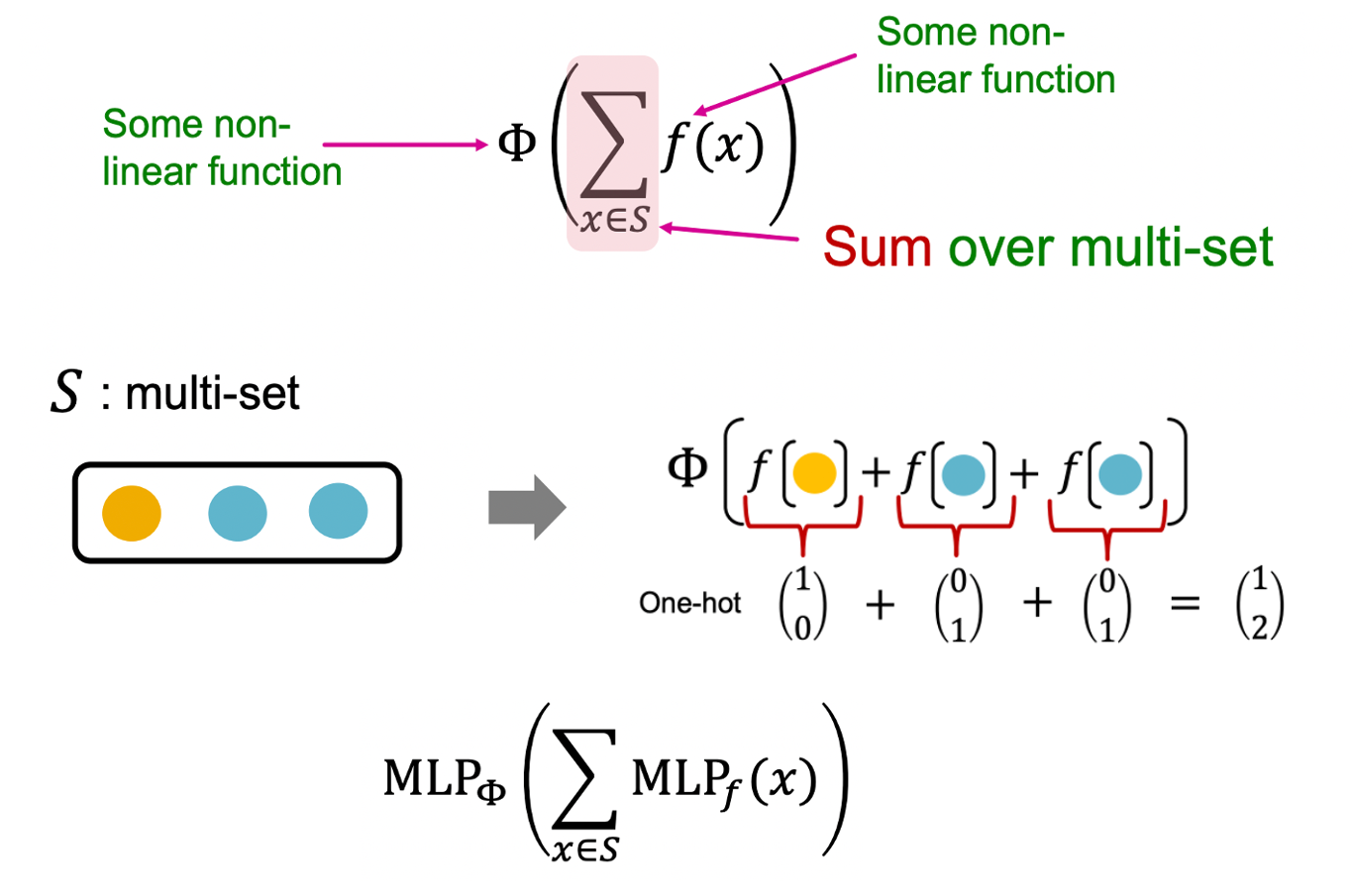
• 각 원소에 대한 비선형 연산인 $f$와 모든 원소의 합에 대한 비선형 연산인 $\phi$를 함께 활용하면 injective function을 만들 수 있다.
• $f$와 $\phi$는 단순하게 MLP를 활용할 수 있다.

GIN with WL Graph Kernel

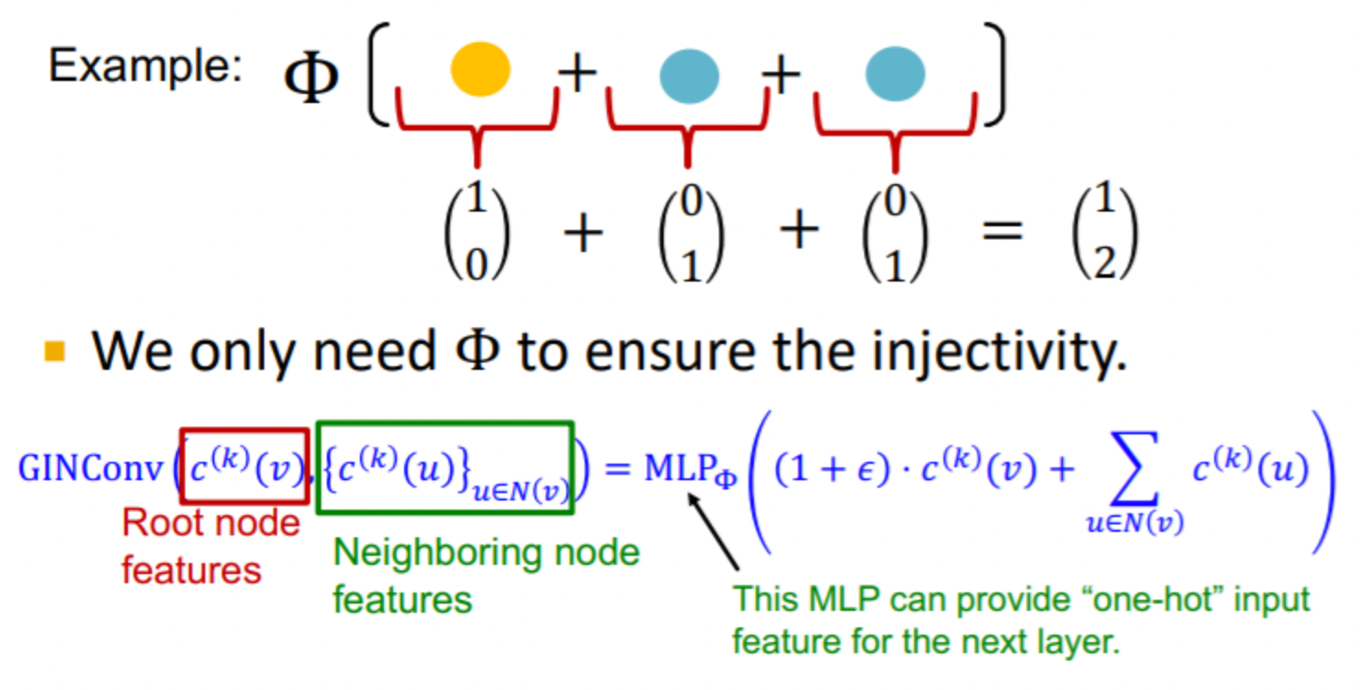
• WL Kernel은 모든 노드에 동일한 초깃값을 설정한 뒤 이웃 노드의 정보를 aggregation하여 반복적으로 해쉬 테이블을 업데이트 하는 방식이다. <Lecture2>
• 이는 단사함수이며 GIN은 해쉬 테이블을 MlP로 변형하여 사용하는 것과 동일하다.
• $MLP_{\phi}$는 자기 자신과 이웃 노드의 벡터를 종합하여 다음 레이어로 전달하며 input과 동일한 형태(one-hot)로 만들어주어 레이어를 거듭해도 정보가 보존될 수 있도록 만들어준다.
• GIN은 저차원 벡터로 구성되어 코사인 유사도 등을 통해 유사도를 계산하기 용이하며, MLP가 학습가능한 파라미터로 구성되어 있기 때문에 downstream task에 맞춰 fine tuning 할 수 있다는 장점이 있다.

References

• Lecture 9.1: https://www.youtube.com/watch?v=5vMEgYbka0A&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=26
• Lecture 9.2: https://www.youtube.com/watch?v=B5y47gWt3co&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=27