1.Message Passing and Node Classification
Correlation
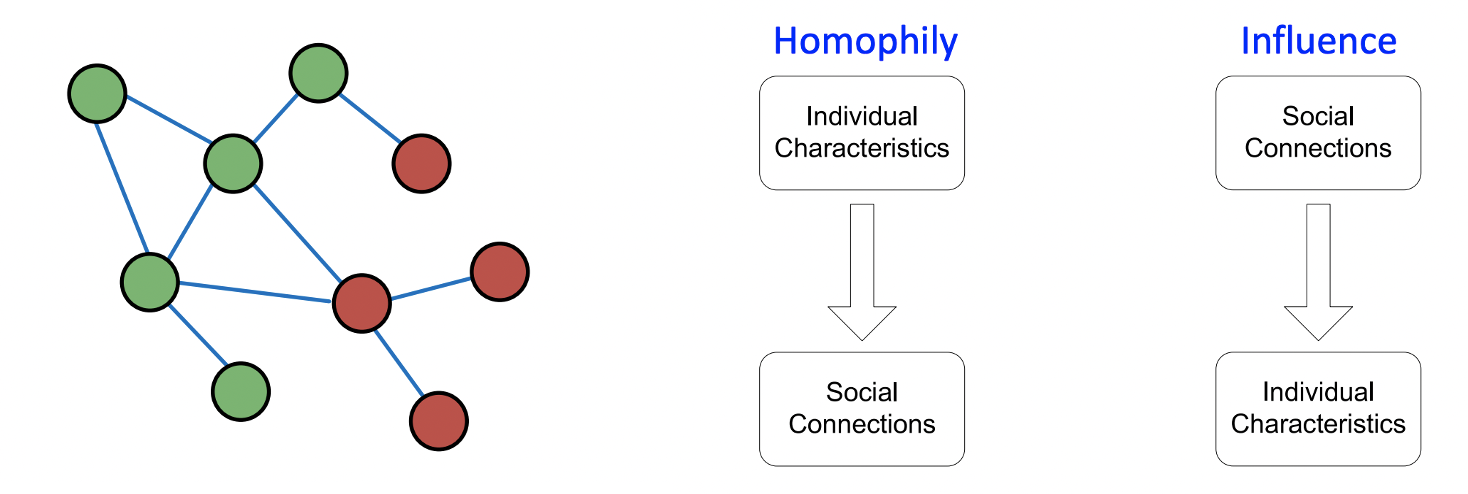
- 가까운 노드들끼리는 같은 클래스에 속한다고 보고 동일한 색을 부여한다.
- 상관관계는 Homophily와 Influence에 의해 정의된다.
Homophily: 비슷한 특성을 지니는 것들끼리 모이는 경향이 있다.
Unfluence: 사회적인 관계가 개인의 특성에 영향을 미친다.
Motivation
- 그래프 상에서 비슷한 노드들은 가까이 위치하거나 서로 연결되어있을 것이라는 가정
- Guilt-by-association: 어떤 노드와 연결되어 있는 노드는 그 노드와 동일한 라벨을 가질 것이다.
- 노드 의 라벨은 의 feature와 의 이웃 노드들의 라벨과 feature에 영향을 받는다.
Semi-supervised Learning
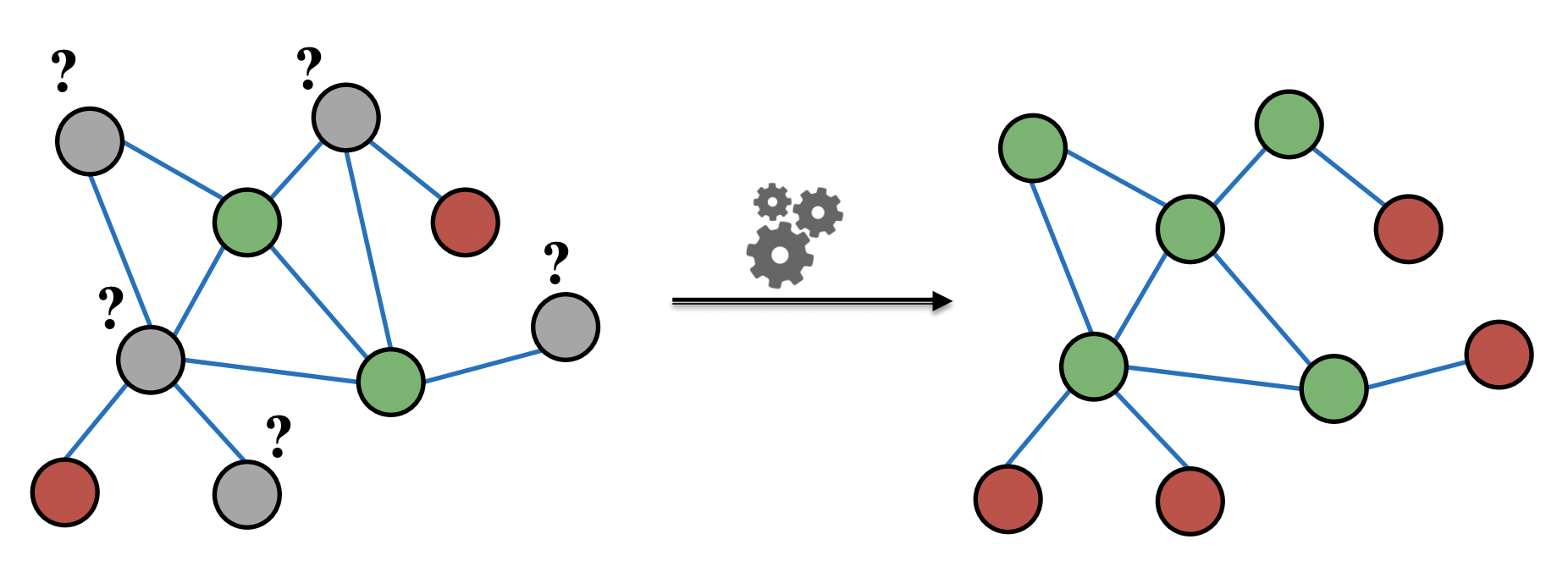
- 일부 노드들의 라벨(color)을 알고 있을 때 나머지 노드들의 라벨을 예측하는 semi-supervised learning
- 네트워크에 homopyiliy가 있다고 가정한다.
Collective Classification
- 상관관계를 이용해 연결된 노드들의 클래스를 동시에 분류한다.
- Markov assumption: 노드 의 라벨 는 이웃노드의 라벨 의 영향을 받는다.
- Collective classification은 3개의 step으로 이루어진다.
1. Local Classifier: 초기 라벨을 할당하는 단계로 노드의 feature를 통해 예측한다.
2. Relational Classifier: 노드 간의 상관관계를 이용하는 단계로 이웃노드들의 feature를 활용하여 예측한다.
3. Collective Inference: 상관관계를 활용하는 classifier를 반복적으로 적용하는 단계로 이웃 노드들 간의 inconsistency가 최소가 될 때 반복을 마친다.
2. Relational Classification and Iterative Classification
Relational classifiers
- 노드 의 class probability 는 이웃 노드들의 class probability의 가중평균으로 정의한다.
- 라벨링 된 노드는 ground truth , 라벨링이 안 된 노드는 로 초기화한다.
- 수렴할 때까지 혹은 최대 반복횟수에 도달할 때까지 랜덤한 순서로 노드를 업데이트 한다.
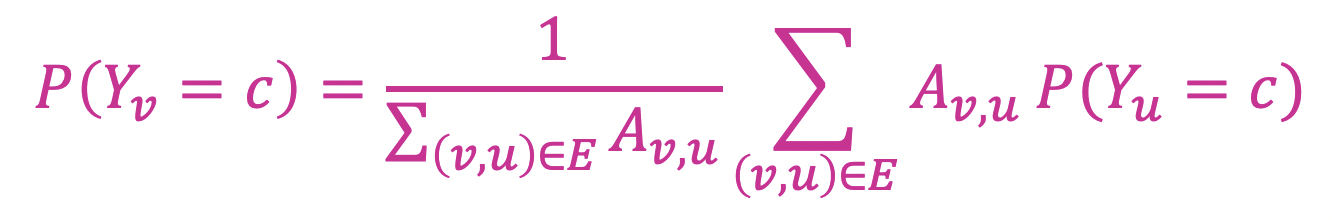
- 는 노드 가 라벨 일 확률을, 는 두 노드 간의 edge weight를 의미한다.
- 수렴이 보장되지 않으며 노드의 feature 정보를 활용하지 않는다는 단점이 있다.
Example
Initialization
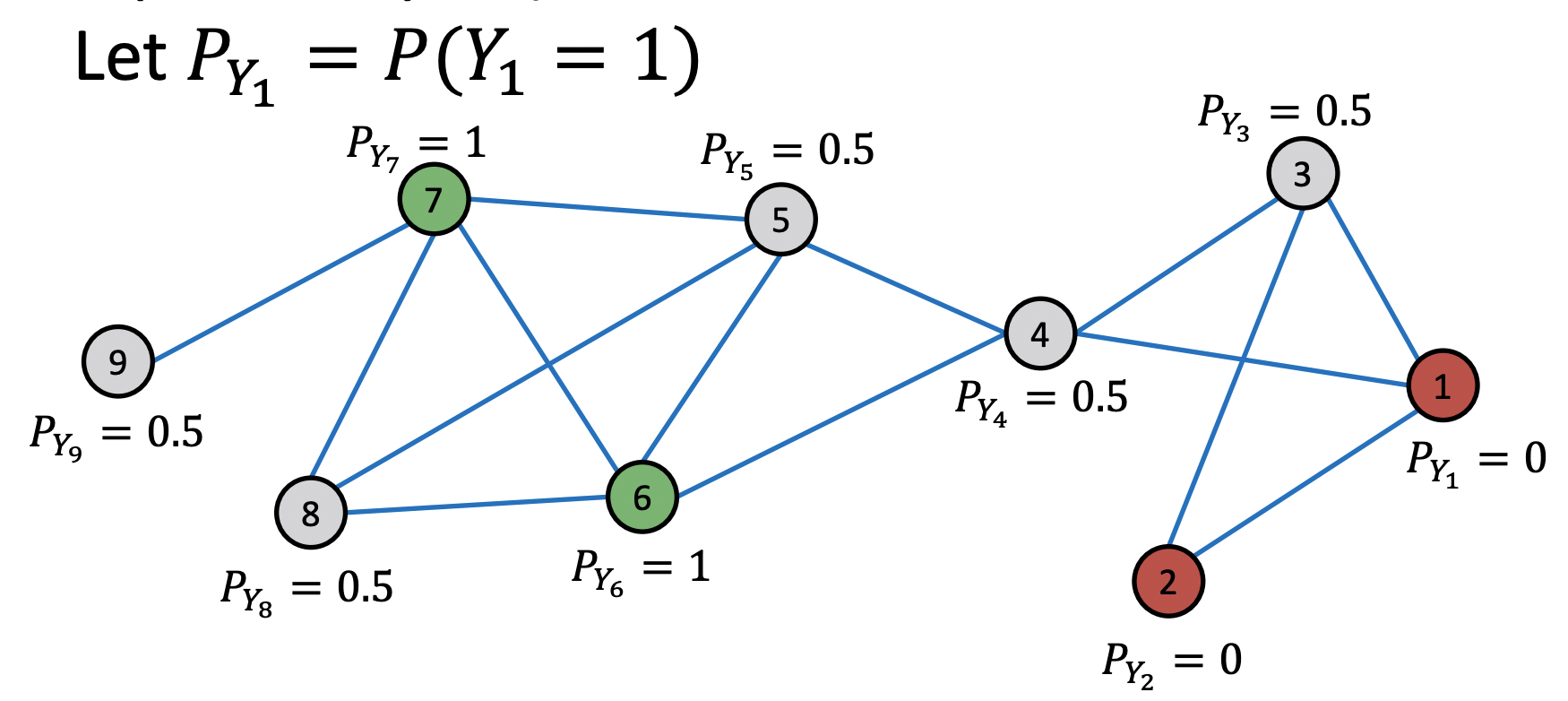
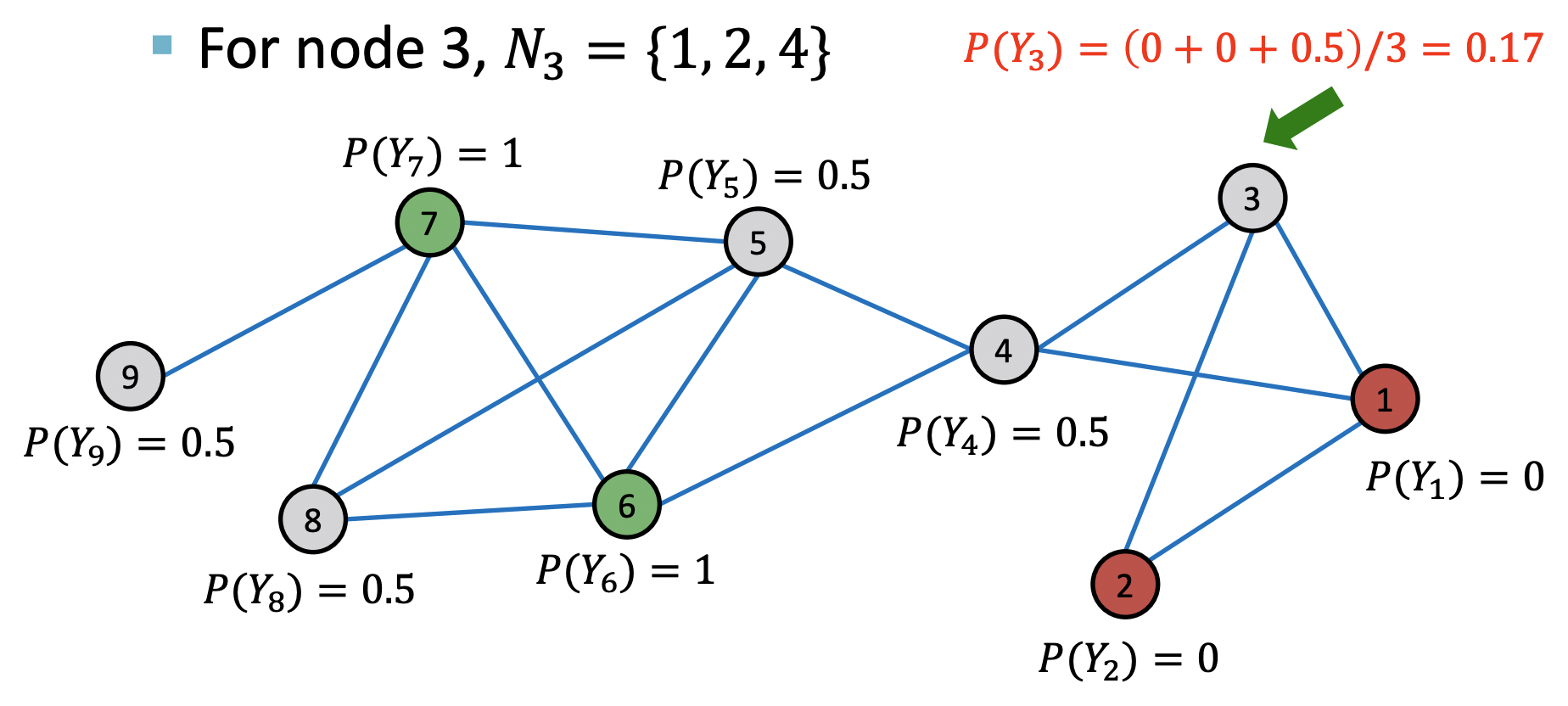
1st iteration, update node3
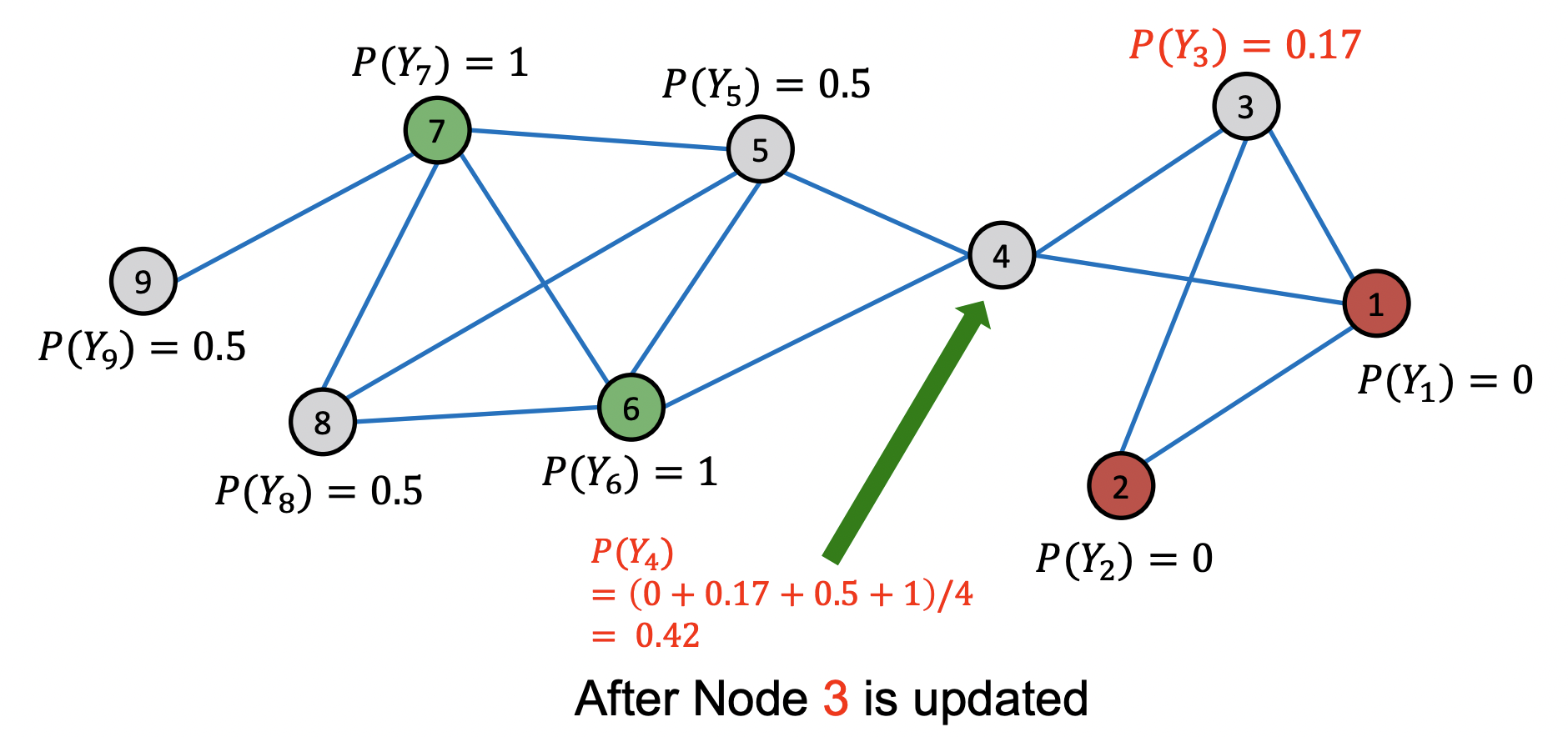
1st iteration, update node4
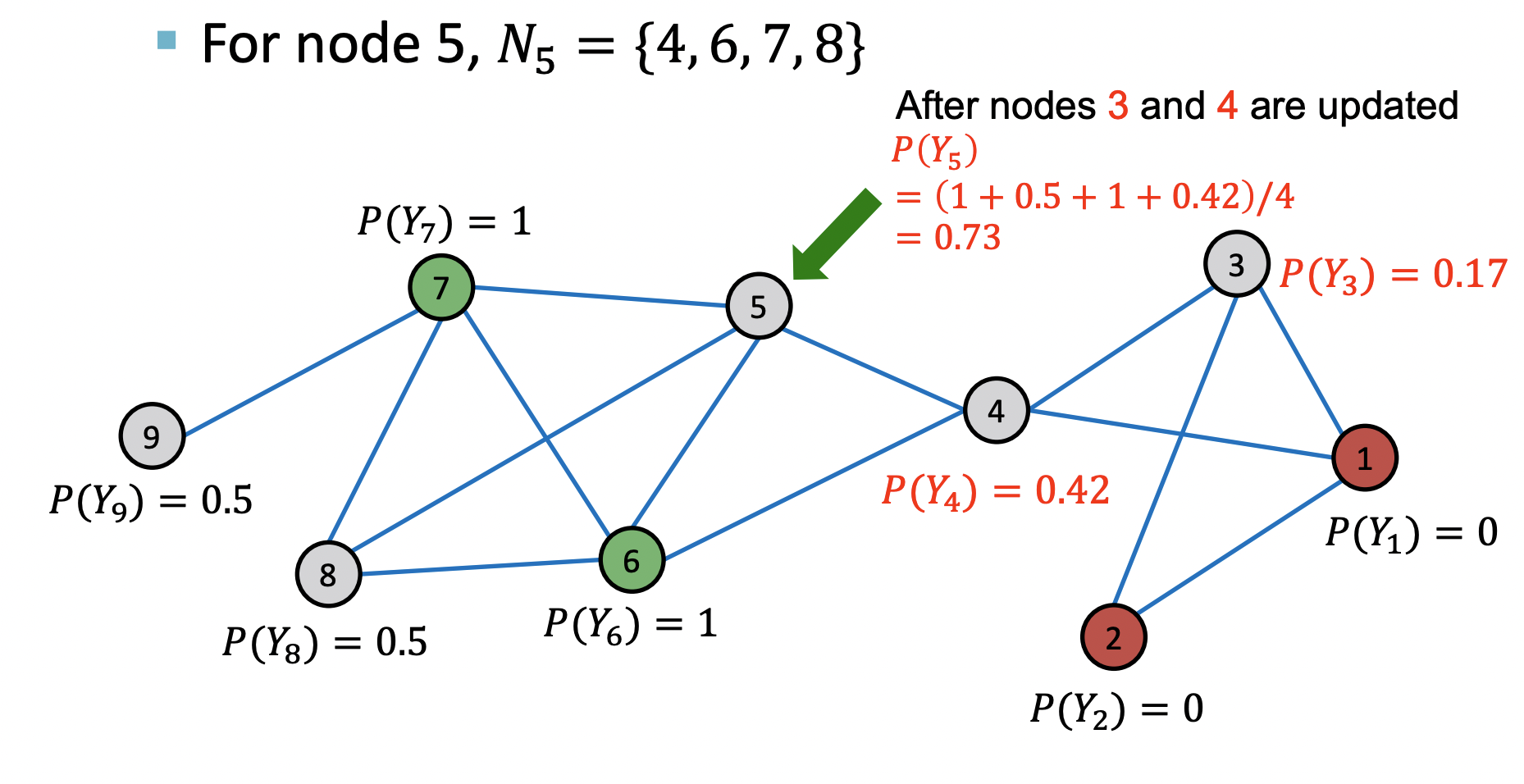
1st iteration, update node5
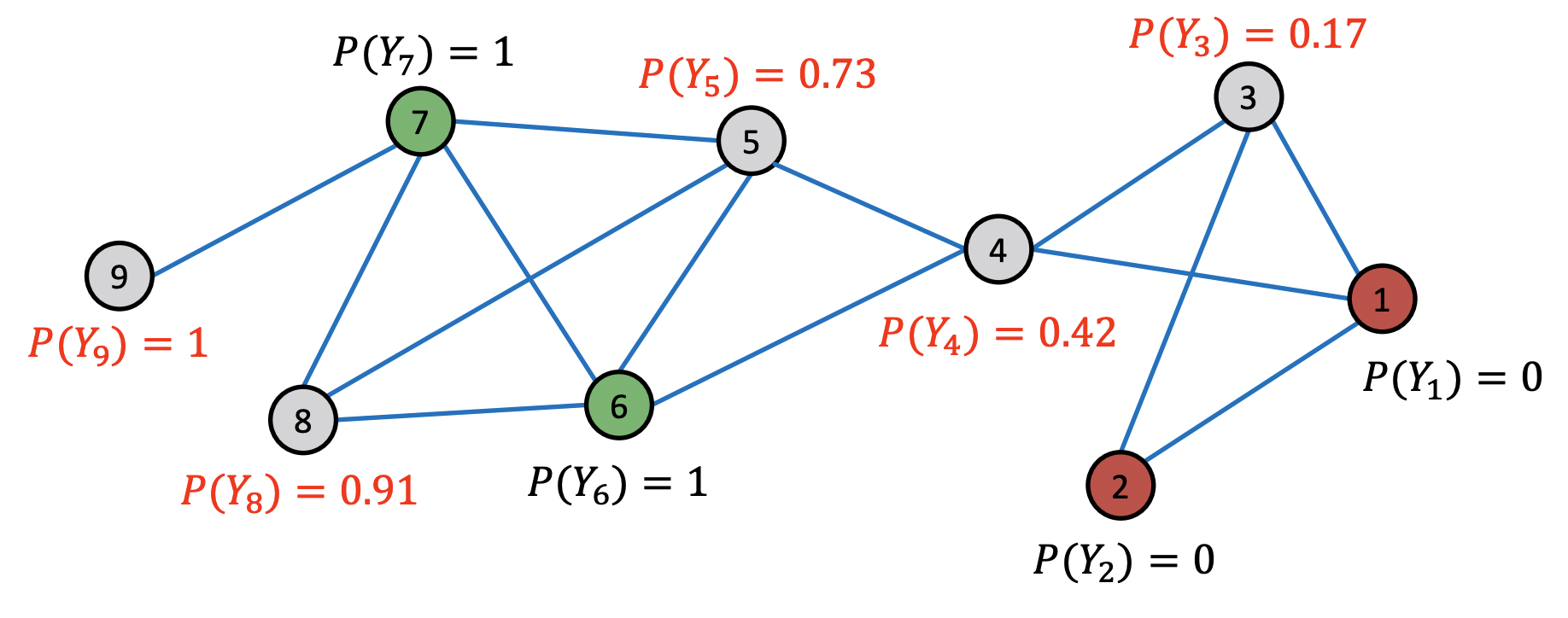
After 1st iteration
After 2nd iteration
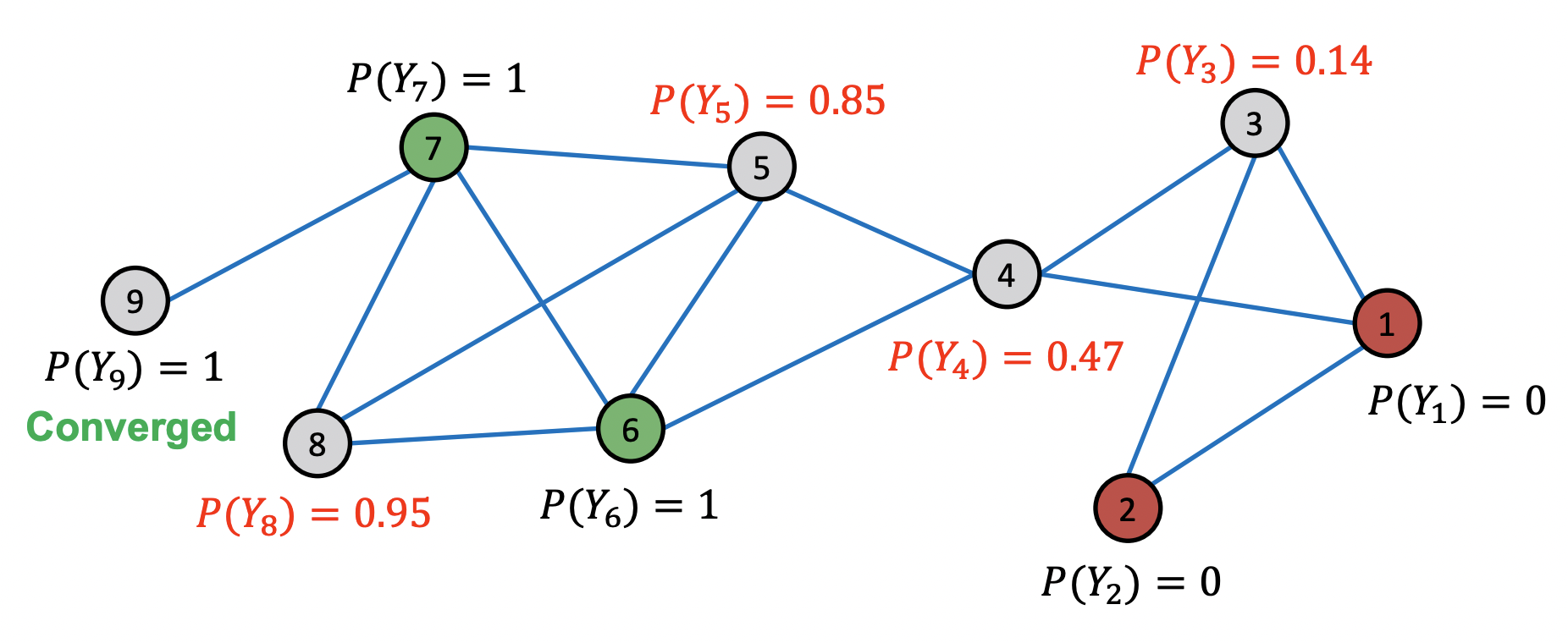
After 3rd iteration
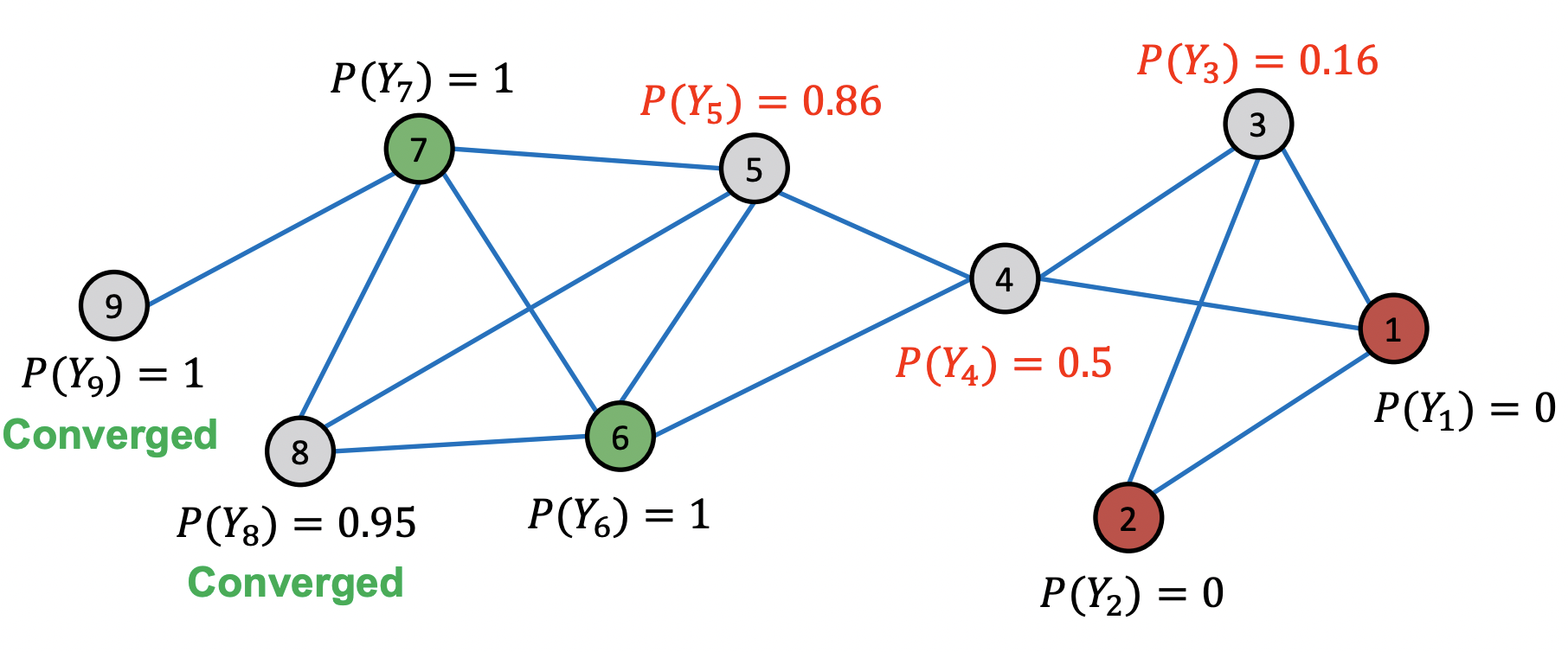
After 4th iteration, Convergence
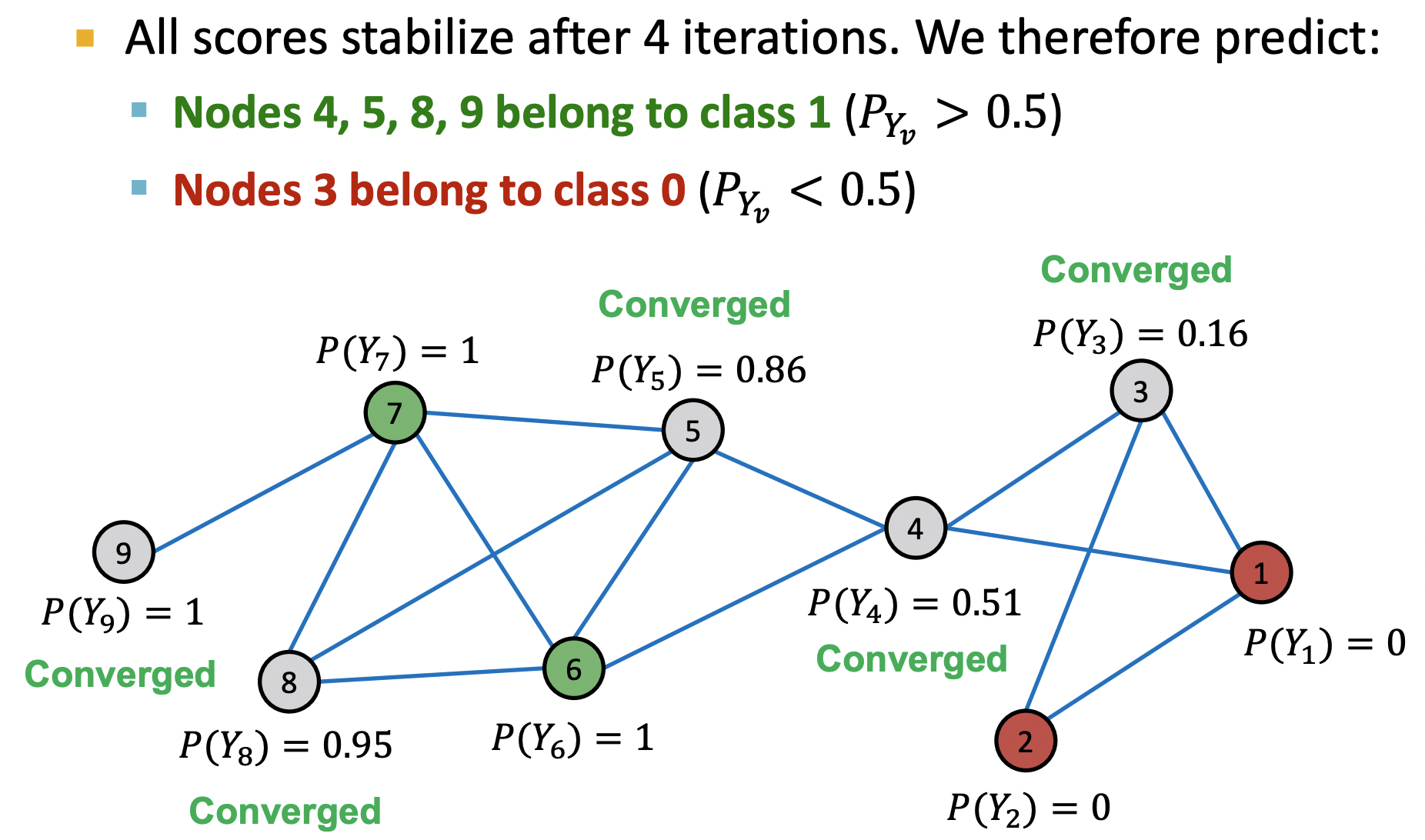
- 4번의 반복 이후 모든 노드들이 수렴했다.
- 가 0.5보다 크면 클래스 1, 작으면 클래스 0으로 분류한다.
Iterative Classification
- 이웃노드 집합 의 summary 와 feature 를 모두 이용해 노드 를 분류한다.
- feature vector로 예측하는 와 feature vector와 summary를 통해 예측하는 두 개의 분류기를 활용한다.
- Summary 는 에서 각 라벨의 수에 대한 히스토그램, 존재 유무, 비율 등에 대한 vector로 정의할 수 있다.
Training
- Training 과정에서는 모든 노드의 라벨을 알고 있다.
- 과 를 통해 를 예측한다.
- 는 실제 라벨을 이용해 구성한다.
Test
- Test 과정에서는 일부 노드의 라벨만 알고 있다. 혹은 모든 노드의 라벨을 모를 수도 있다.
- 는 변하지 않을므로 는 한 번만 계산하여 를 예측한다.
- 을 통해 할당한 초기 를 토대로 아래 과정을 수렴 혹은 최대횟수에 도달할 때까지 반복한다.
- 를 통해 를 업데이트한다.
- 를 통해 를 업데이트한다.
Example
Input: 웹페이지의 그래프
Node: 웹페이지
Edge: 웹페이지를 연결하는 하이퍼링크(Diredcted)
Node feature: 웹페이지 description
Task: 각 웹페이지의 주제 예측
: 각 노드의 feature vector(TF-IDF 등)
: Incoming neigbor 라벨에 대한 summary([0인 이웃노드 유무, 1인 이웃노드 유무])
: Outgoing neigbor 라벨에 대한 summary([0인 이웃노드 유무, 1인 이웃노드 유무])
Training
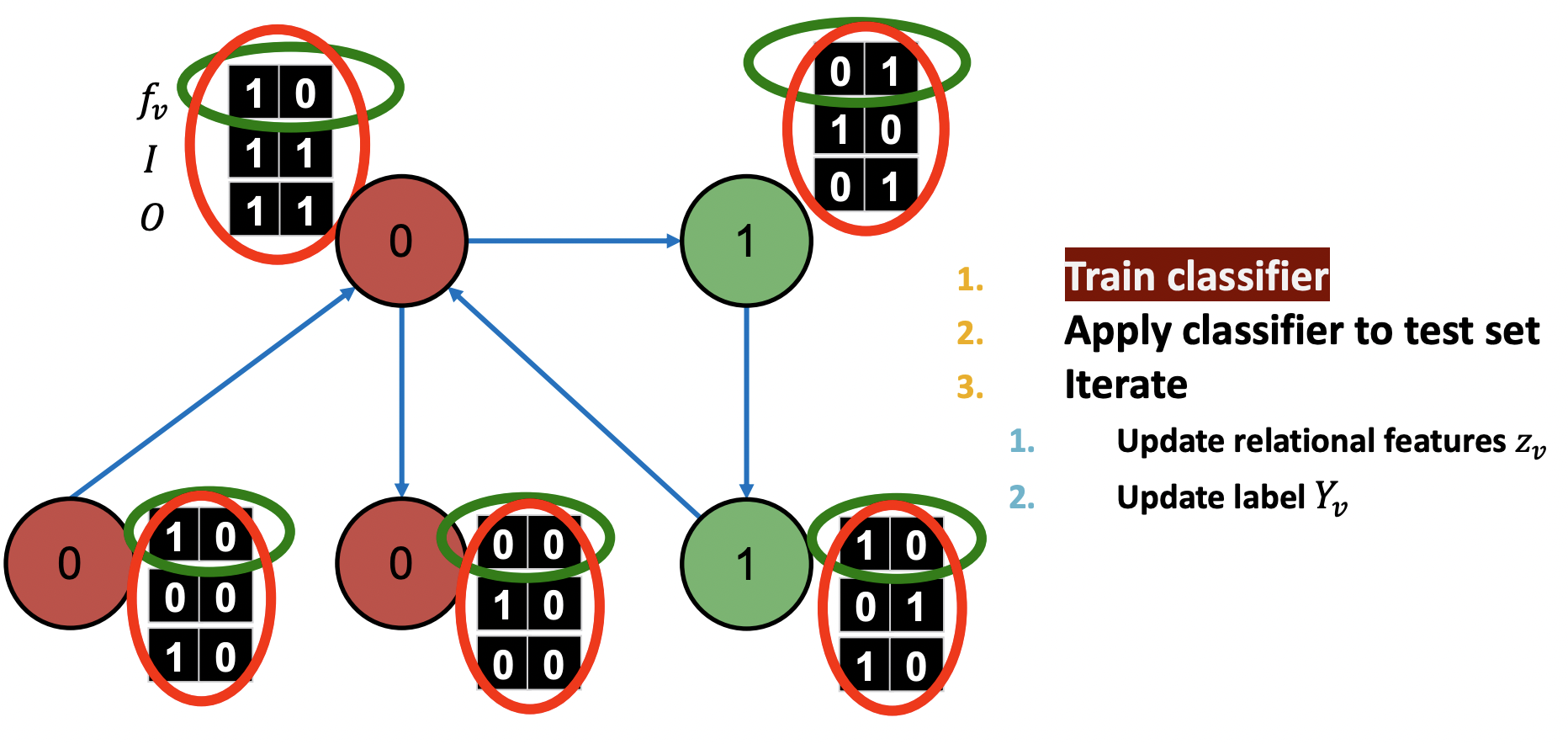
- Feature vector(green)만을 활용해 로 예측
- Feature vevtor와 summary(red)를 활용해 로 예측
Test
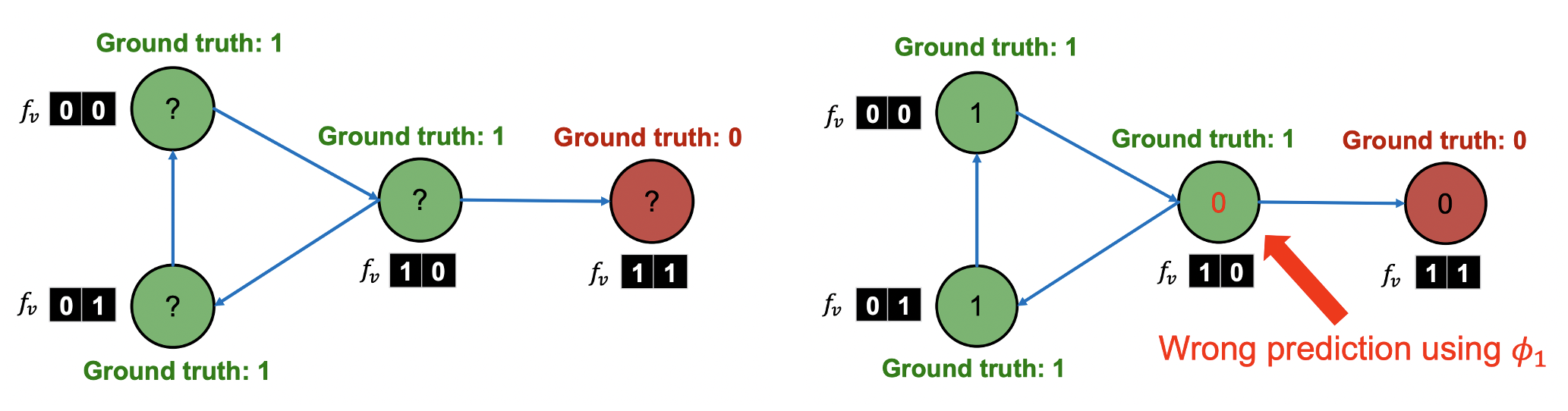
- 학습된 을 통해 를 예측한다.
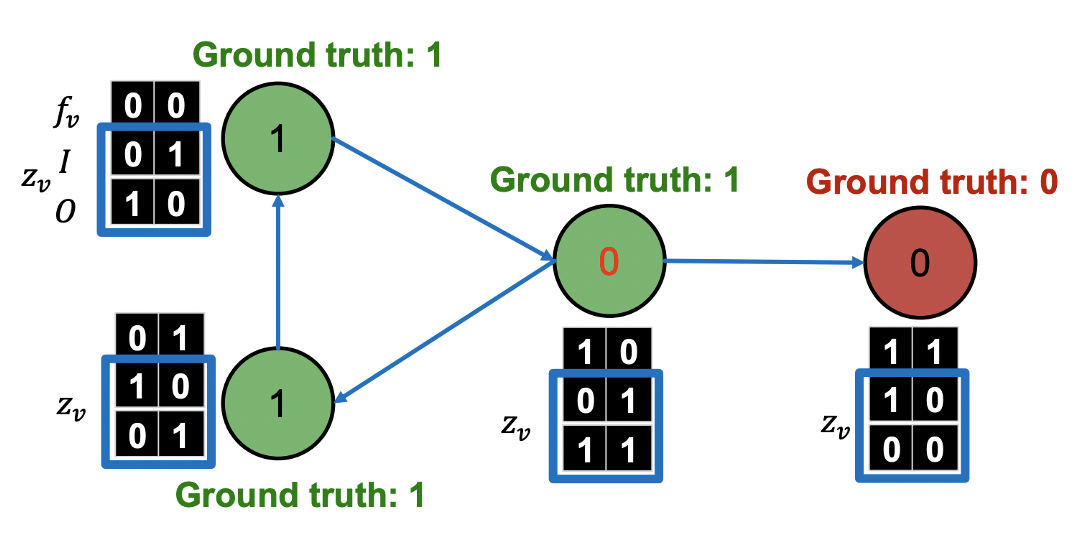
- 예측한 를 통해 를 업데이트한다.
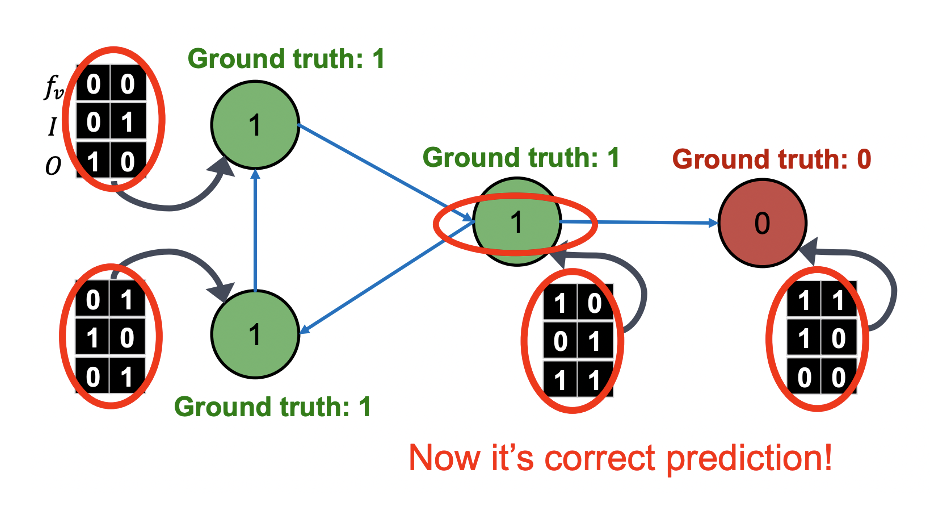
- 와 새로운 를 통해 를 업데이트 한다.
- 위 과정은 수렴할 때까지 반복하며 예시에는 한 번의 반복만으로 GT를 맞춘 것을 확인할 수 있다.
3. Collective classification: Belief Propagation
Loopy Belief Propagation
- 앞서 본 방식에서는 노드 의 클래스 확률을 이웃 노드의 확률의 가중평균으로 정의하였다.
- 이를 이웃노드로부터 belief를 전달받는다고 말하며 반복을 통해 이웃노드 뿐만 아니라 간접적으로 연결된 노드(ex.이웃노드의 이웃노드)로부터도 영향을 받는다고 할 수 있다.
- Loopy belief propagation은 간접적인 방식이 아닌 belief가 그래프에 직접 흐르도록 알고리즘을 구성하는 것을 의미한다.
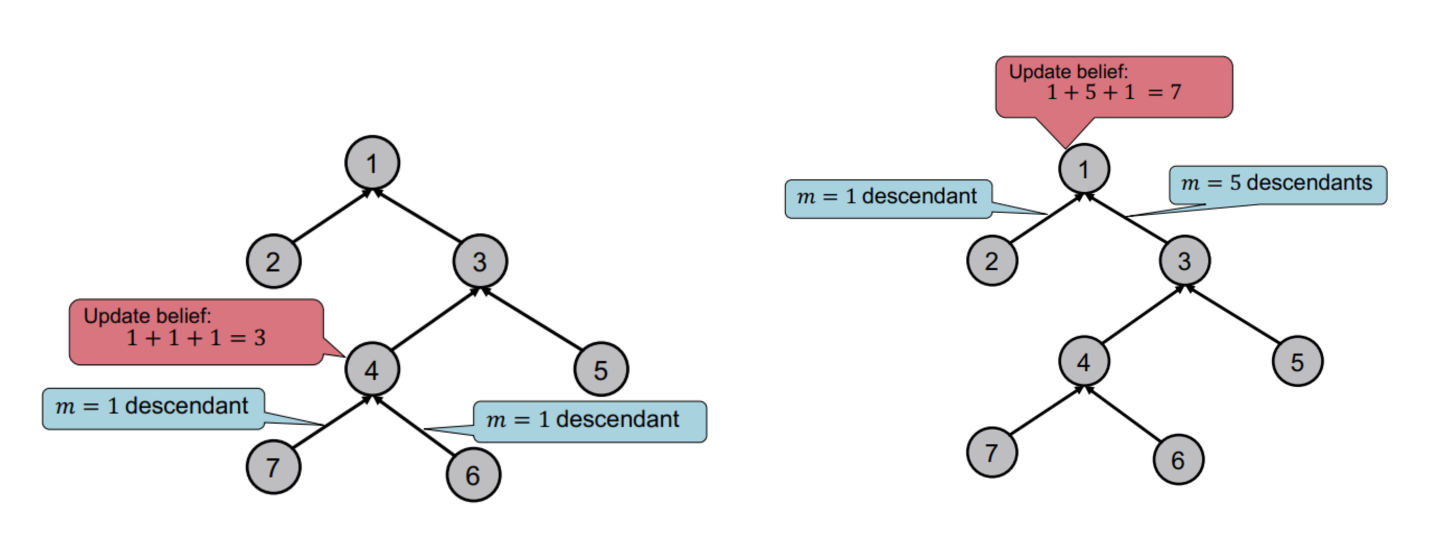
- 예를 들어, 트리 구조에서 그래프의 노드 수를 계산할 때는 child->parent 방향으로의 belief를 생각할 수 있다.
- 노드의 belief(이전까지 지나온 노드의 수)에 자기 자신 1을 더하면 노드까지의 노드의 수를 구할 수 있다.
Algorithm
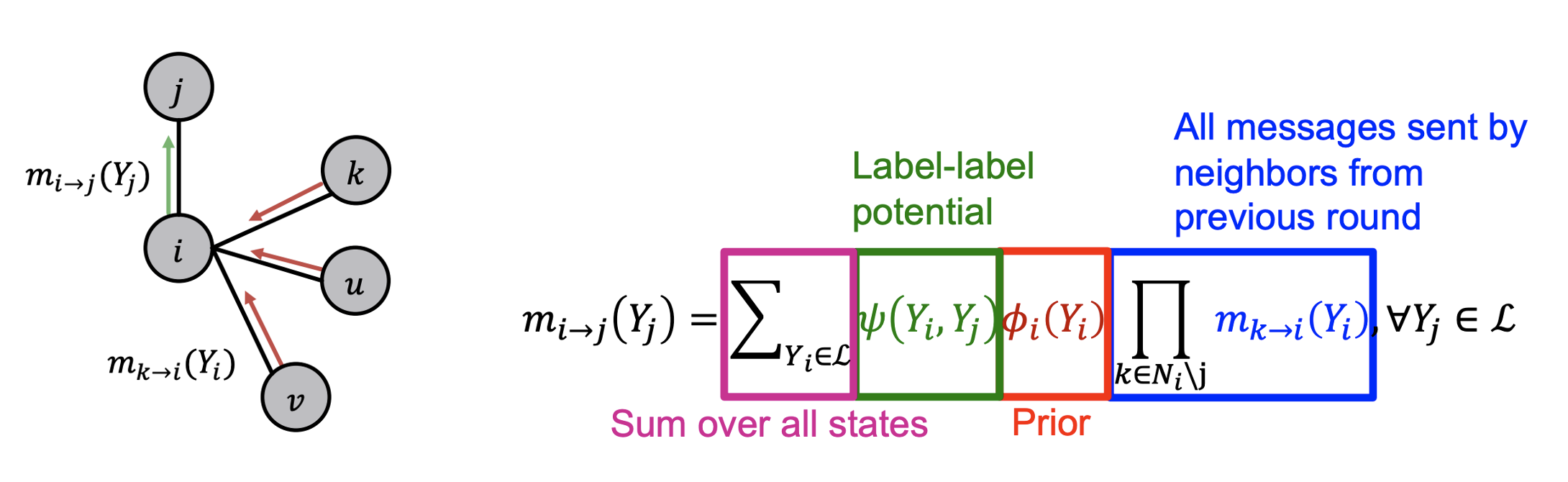
- : 각 노드가 이웃노드의 클래스에 미치는 영향력을 나타낸 행렬. 는 노드 의 라벨이 일 때 노드 가 클래스에 속할 확률에 비례한다.
- (prior beleif): 노드 가 에 속할 확률
- 로 전달되는 의 메시지로 가 이웃노드들로부터 받은 belief와 자신의 정보를 종합해 의 라벨을 believe하는 것
- 모든 라벨을 포함하는 집합
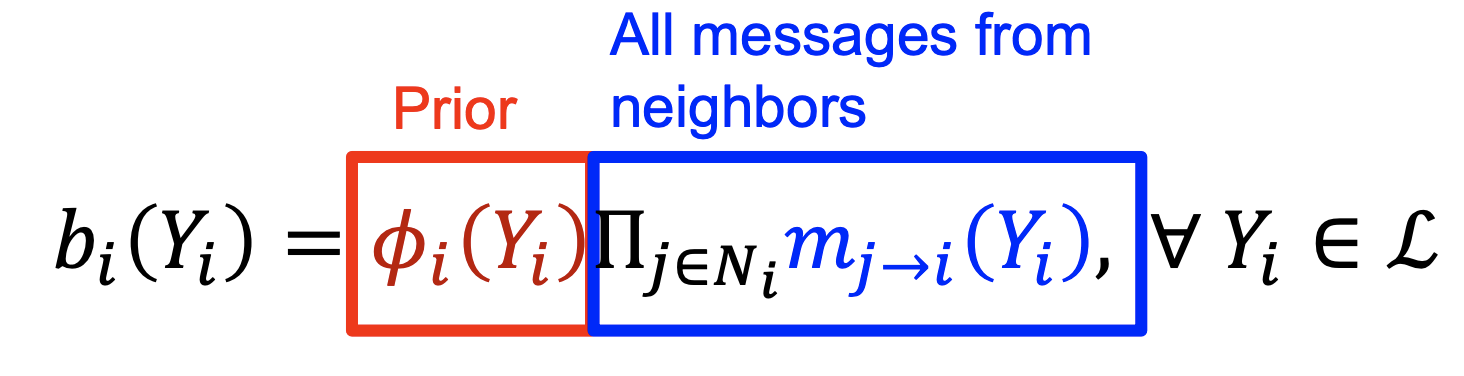
- message passing 과정이 충분히 반복되어 수렴되었을 때 위 식과 같이 확률이 계산된다.
What Can Go Wrong?
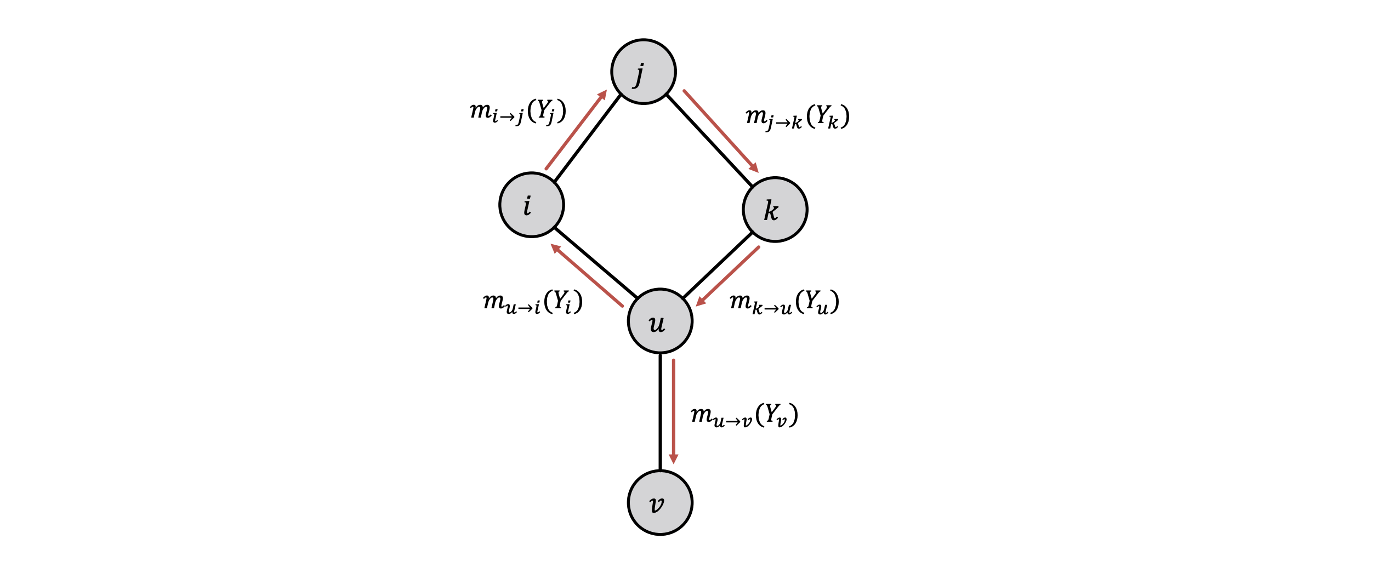
- 그래프가 순환구조인 경우 노드들은 독립적이지 않다.
- 노드 는 로부터 메시지를 받고 있지만 결국 자기 자신의 메시지까지 받는 상황이다.
- 반대로 가 로 메시지를 전달하고 가 로 메시지를 전달한다면 의 메시지는 에게 중복 전달하게 된다.
- 부분적으로는 이러한 문제점이 크게 나타날 것 같지만 실제로는 전체 구조가 매우 크고 복잡하여 Loopy BP 알고리즘은 잘 작동한다.
References
- Lecture 5.1: https://www.youtube.com/watch?v=6g9vtxUmfwM&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=14
- Lecture 5.2: https://www.youtube.com/watch?v=QUO-HQ44EDc&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=15
- Lecture 5.3: https://www.youtube.com/watch?v=kh3I_UTtUOo&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=16
