<CS224W> Lecture 4: Graph as Matrix
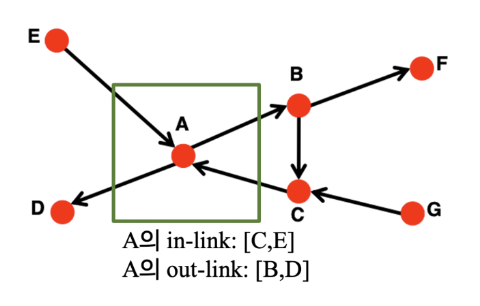
- 웹은 각 웹페이지가 노드, 페이지 간의 하이퍼링크가 엣지인 그래프로 표현할 수 있으며 각 웹페이지는 서로 다른 중요도를 가진다.
- 웹에는 방향성이 있어 해당 웹페이지로 연결되는 in-link와 다른 웹페이지로 연결되는 out-link가 있다.
The "Flow" Model
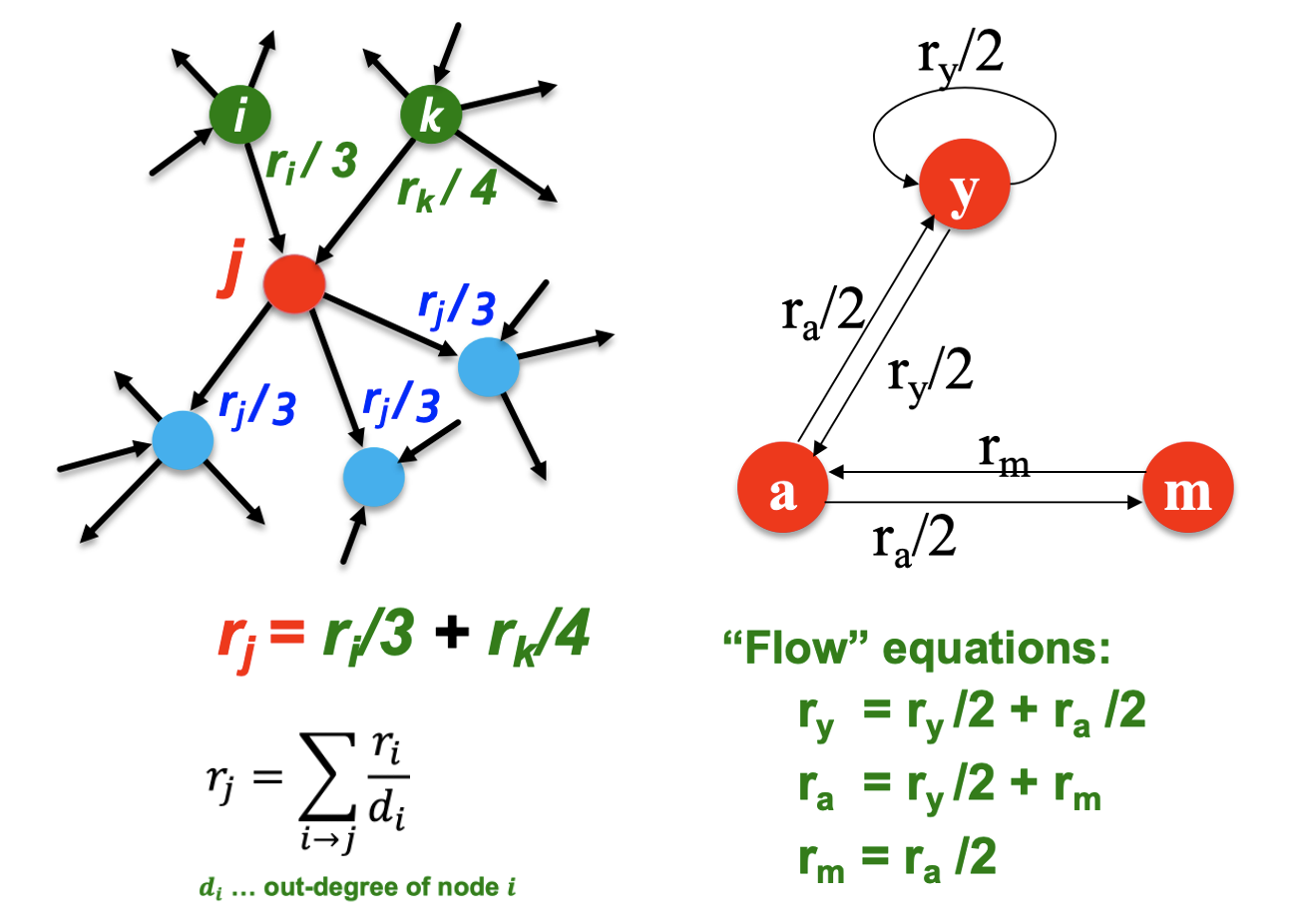
- In-link가 많을수록 중요도가 높으며 in-link가 같을 경우 중요한 페이지로부터 들어온 link가 많은지로 중요도를 판단하여 recursive한 문제가 된다.
- In-link는 vote로 볼 수 있으며 page i의 중요도가 ri이고 out-links가 di개면 각 링크들은 ri/di의 votes를 가지게 된다.
- Page j의 rj는 모든 votes의 합이 된다.
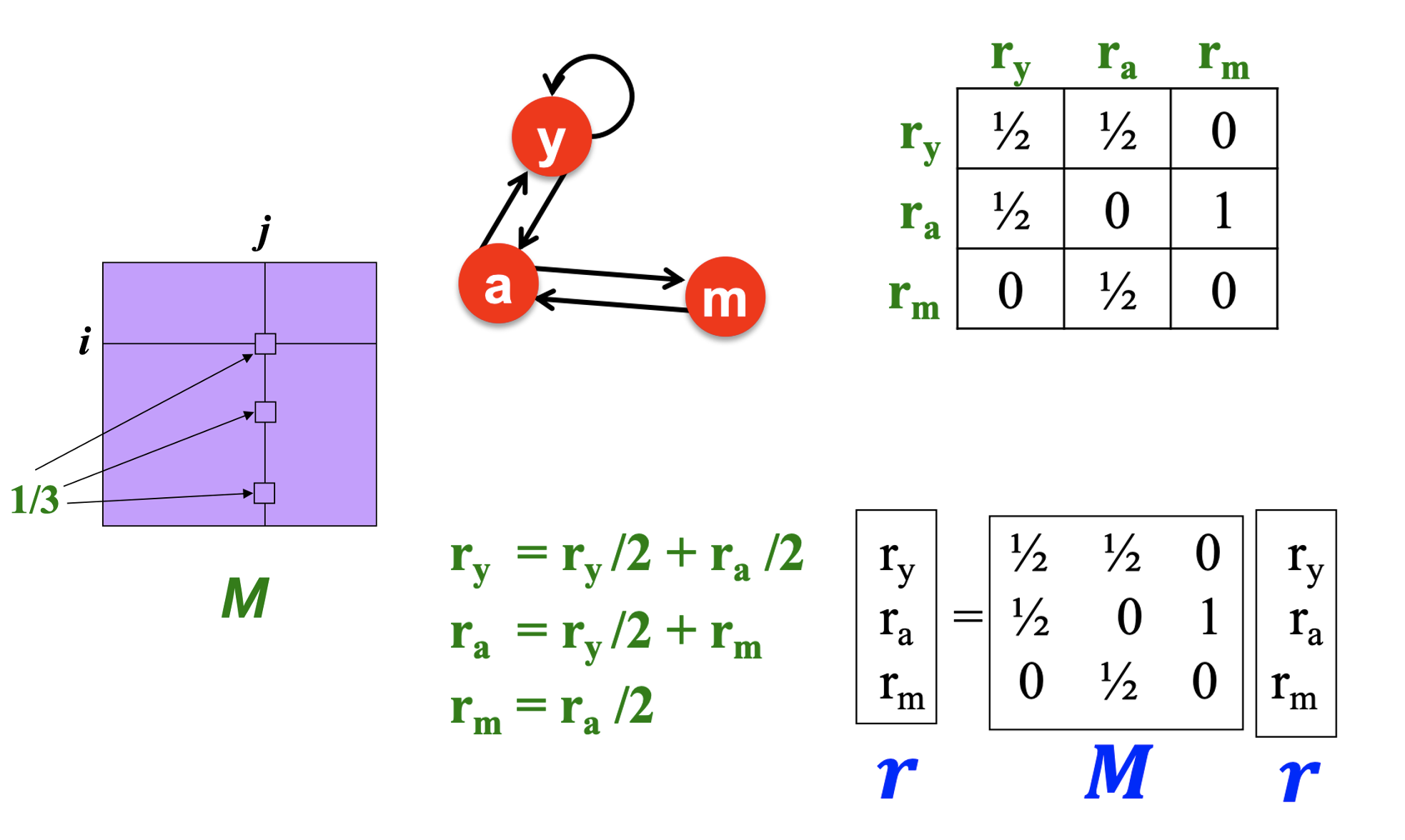
- Page j가 dj개의 out-links를 가질 때 j에서 i로 가는 link가 있다면 Mij=dj1이다.
- Page 별 중요도에 대한 벡터를 r이라 할 때 r=M⋅r로 나타낼 수 있다.
Stationary Distribution
- p(t)는 균일한 확률로 random walk하는 surfer가 t 시점에 page i에 있을 확률이 i번째 원소에 담긴 벡터이다.
- t+1 시점의 surfer의 위치는 p(t+1)=M⋅p(t)가 된다.
- Random walk가 state에 도달하면 p(t+1)=M⋅p(t)=p(t)로 더 이상 변하지 않는 stationary distribution 상태이다.
- 중요도 벡터도 r=M⋅r로 같은 형태이므로 stationary distribution이라 할 수 있다.
2. How to solve?
Power Iteration
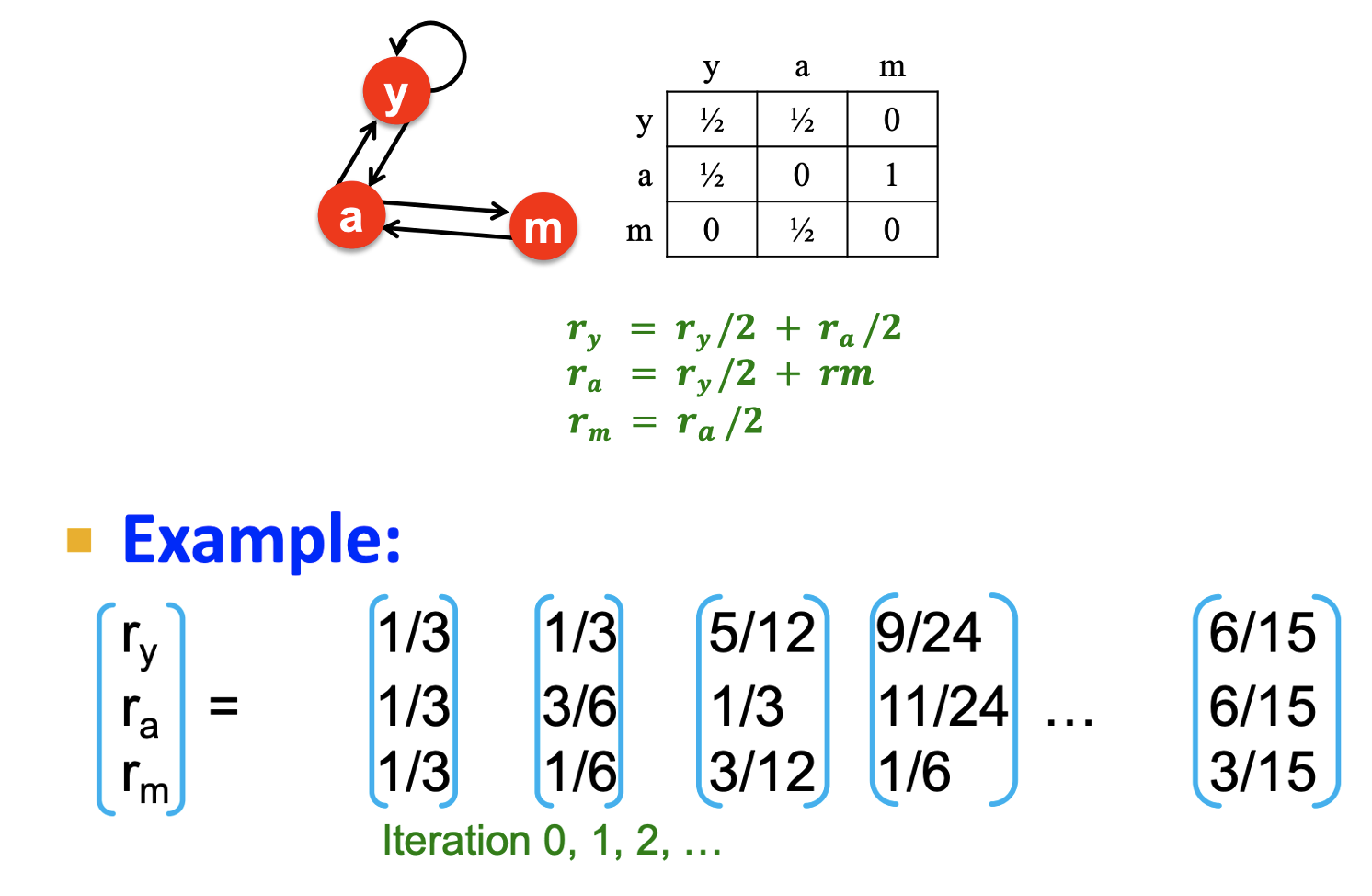
- Flow 방정식이 1⋅r=M⋅r이므로 고유값이 1이고, 중요도 벡터 r이 고유벡터라고 볼 수 있다.
- 우리는 Random walk에서 strationary distribution 상태로 존재하는 중요도 벡터 r을 찾기 위해 ∑i∣∣∣rit+1−rit∣∣∣<ϵ로 수렴할 때까지 M(M(...M(Mu)))로 반복 계산을 한다.
Problems

- Dead ends: out-link가 없는 경우 M이 column stochastic하지 않아(column의 합이 1이 아닌) 중요도에 leakage가 발생한다.
- Spider traps: 모든 out-links가 그룹 안에 속할 때 한 번 들어가면 갇히는 현상이 발생해 해당 page가 중요도를 흡수한다.
Solutions
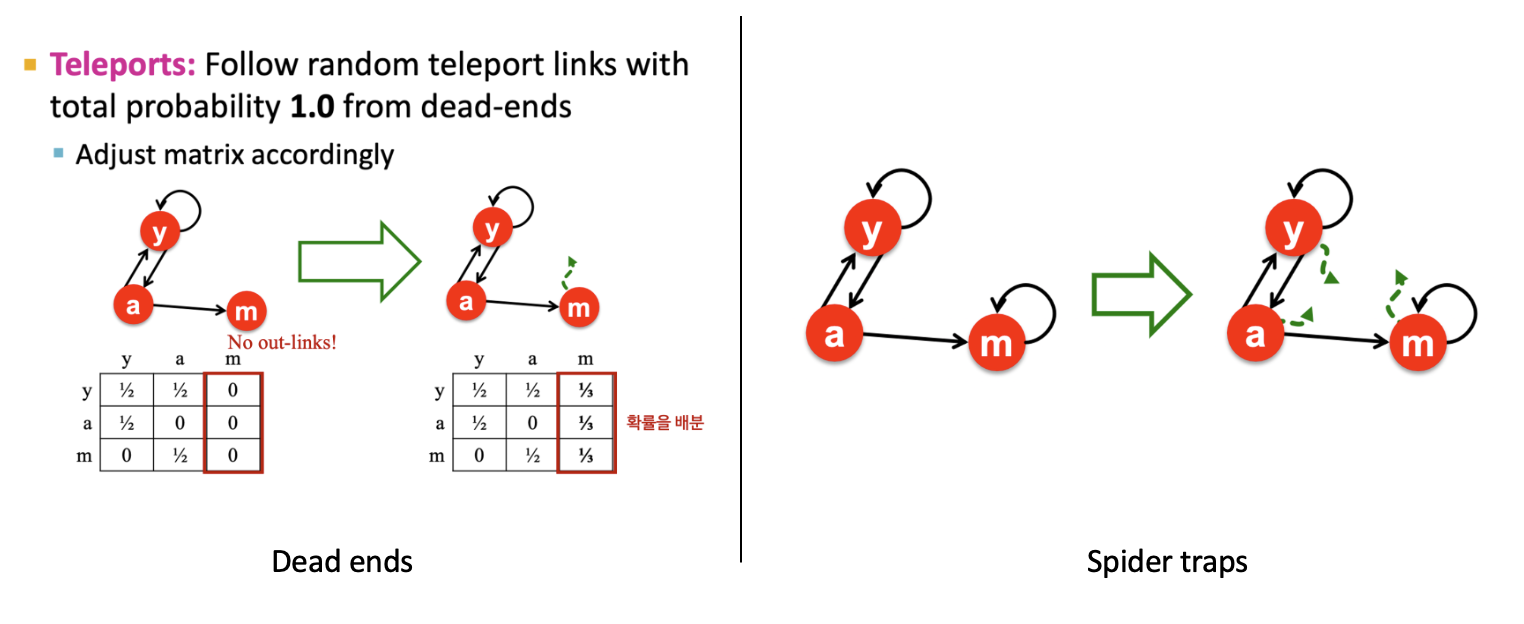
- Dead ends: 확률을 배분하여 column stochastic을 만족시킨다.
- Spider traps: Random teleport를 활용하여 β의 확률로 기존의 link를 타고 이동하거나 (1−β)의 확률로 연결되지 않았던 페이지로 이동한다.
Google Matrix
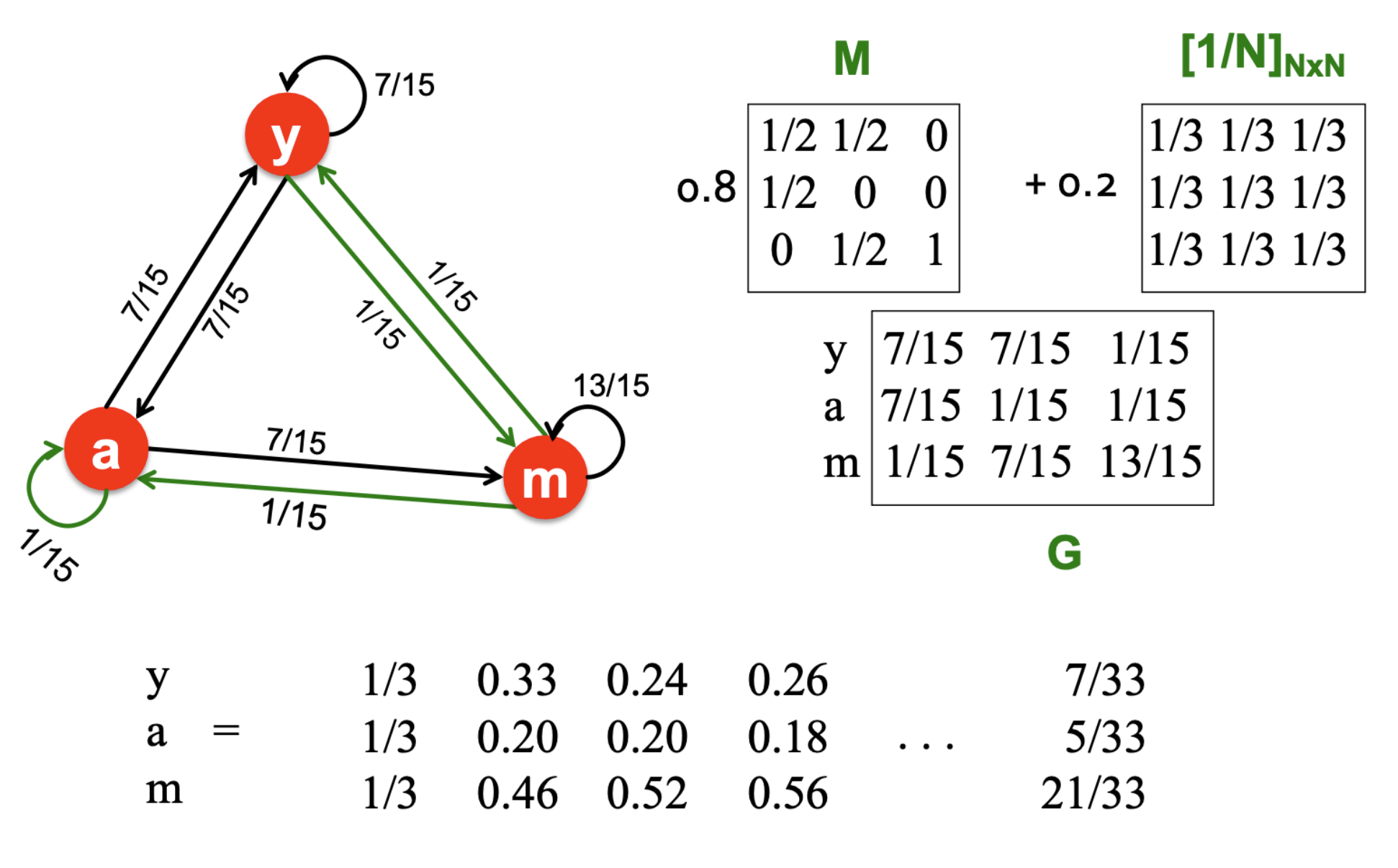
- Random teleport을 포함한 PageRank의 방정식은 rj=∑i−>jβdiri+(1−β)N1이다.
- 따라서, Google matrix G=βM+(1−β)[N1]NxN로 표현되며 PageRank는 r=Gr을 푸는 문제가 된다.
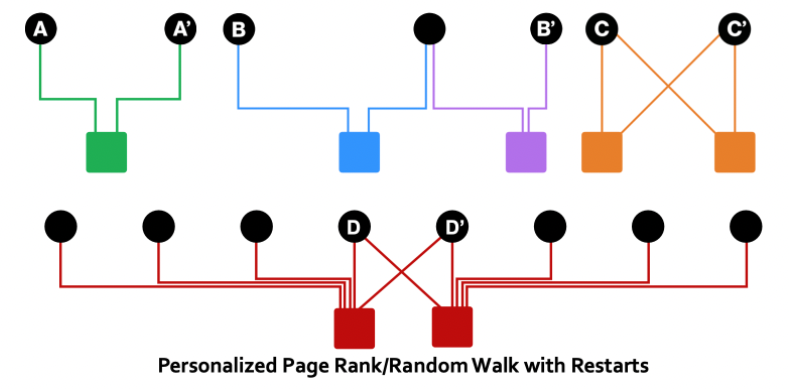
- 위 그래프는 사용자(사각형)와 아이템(원)으로 이루어진 biparatite graph이다.
- (C,C′),(A,A′),(B,B′) 순으로 연관성이 큼을 알 수 있고 (D,D′)는 사용자가 너무 많은 아이템을 구매하여 우연성이 있기 때문에 (C,C′)만큼 연관성이 크다고 보기는 어렵다.
- 이를 표현하기 위해 중요도를 기반으로 rank를 설정하고 전체 노드 간에 랜덤하게 텔레포트를 하는 PageRank와 다른 Personalized PageRank와 Random Walks with Restarts가 있다.
- 텔레포트가 될 확률을 일부 노드끼리만 균일하게 혹은 가중치를 반영하여 설정한다.
- 텔레포트 행렬을 T라 하면 열벡터는 다음과 같다.
[T1j,T2j,...,TNj]=[0.2,0,0,0,0,0.4,0,0,0.4]
Random Walks with Restarts
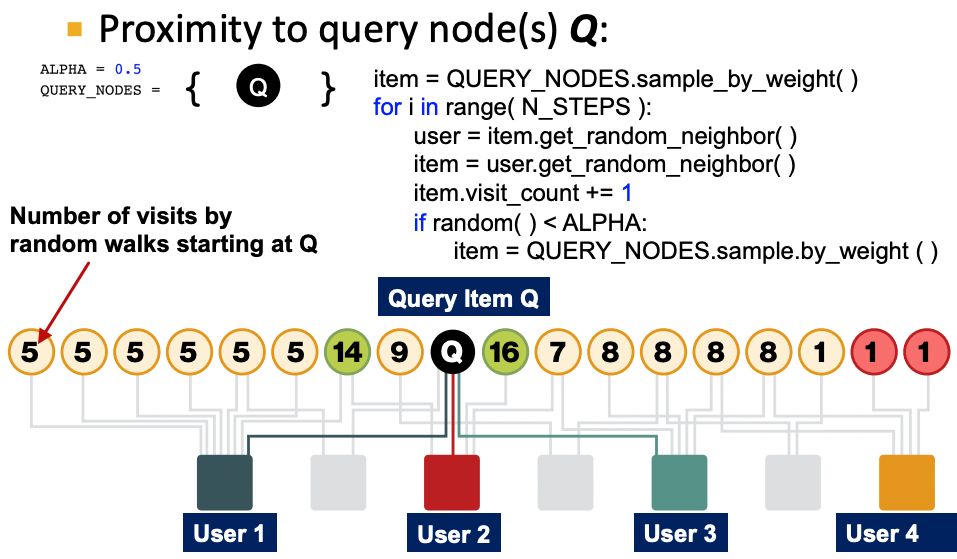
- 랜덤워크를 재시작할 노드에만 확률값 1을 부여한다.
[T1j,T2j,...,TNj]=[0,0,0,0,0,1,0,0,0]
- ALPHA는 랜덤워크를 재시작할 확률이다.
- 시작 노드와 특정 노드 간에 엣지가 많거나, 경로가 많거나, 직접 연결되어 있거나, degree가 낮은 사용자로 연결되어 있다면 랜덤워크에서 많이 방문하게 되고 유사도가 높아진다.
4. Matrix Factorization
Simple Matrix Factorization
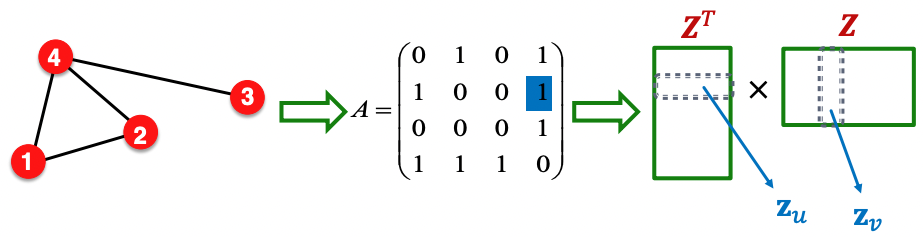
- 임베딩 행렬 Z의 column은 각 노드의 embedding vector를 담고있다.
- 비슷한 노드=연결되어 있는 노드라는 관점에서 인접 행렬 A의 요소는 z의 내적과 같다.
zv⊤zu=Auv
- 임베딩 벡터의 차원 d는 일반적으로 노드의 수보다 훨씬 작아 정보를 담기에 충분하지 못하므로 Z⊤Z=A를 근사시키기 위해 다음과 같은 목적함수를 사용한다.
minZ∣∣A−Z⊤Z∣∣2
Random Walk-vased Similarity
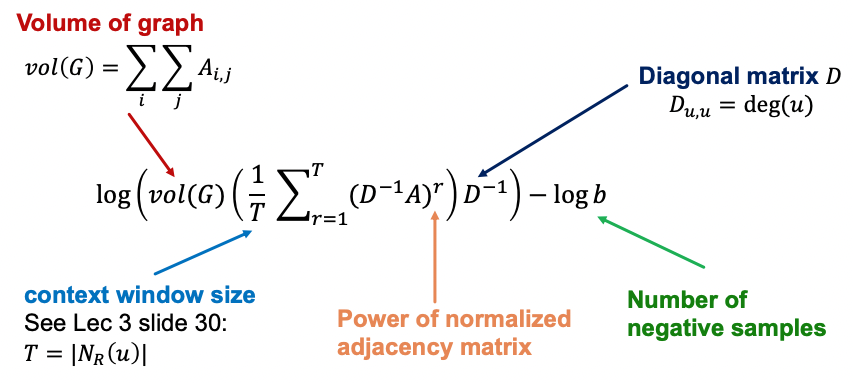
- DeepWalk나 node2vec은 노드 유사성에 대해 복잡한 정의를 내리고 있다.
- r은 랜덤워크의 step 수, T는 전체 윈도우 사이즈, D는 각 노드의 degree에 대한 대각행렬이다.
5. Limitation of node embedding via matrix factorization and random walks
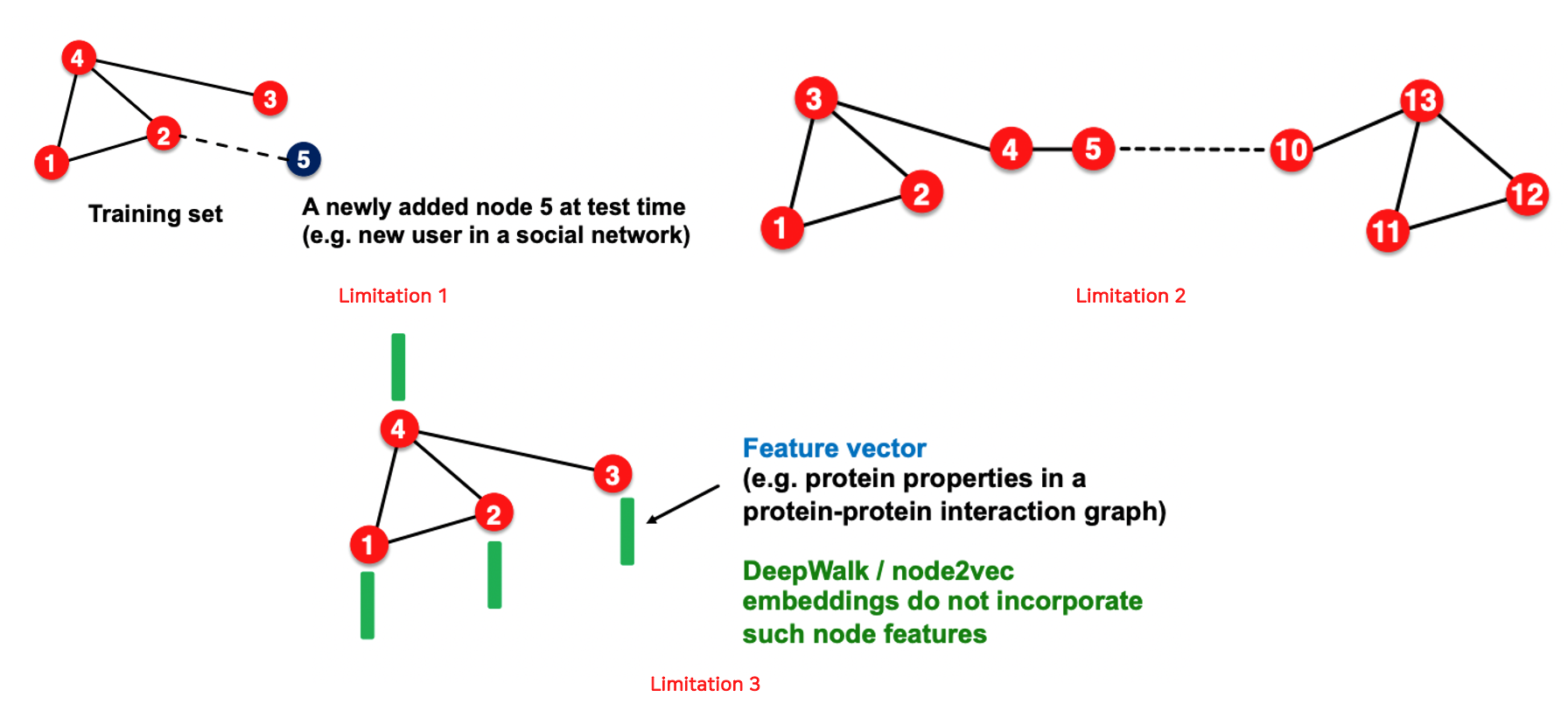
- 훈련 시 학습되지 못한 노드의 임베딩 벡터를 만들 수 없다.
- 구조적 유사성을 잡아낼 수 없다. 1번 노드와 11번 노드는 비슷한 구조이지만 서로 다른 embedding vector를 가진다.(Anonymous walk의 경우 잡아낼 수 있기는 하다.)
- 노드, 엣지, 그래프의 feature를 활용할 수 없다.
References













