Components of Graph

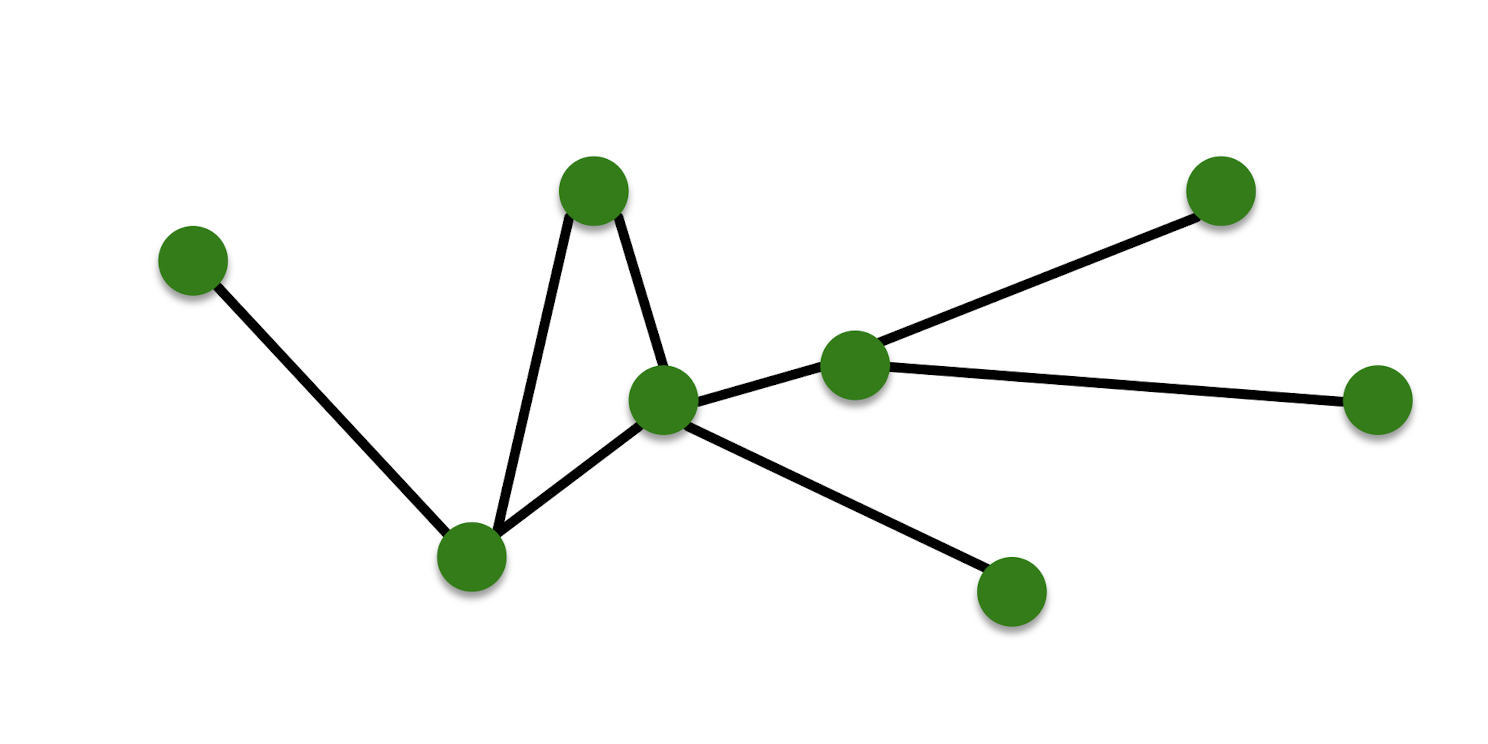
• Objects는 nodes(vertices)에 담기며 $N$으로 표기한다.
• Interactions는 edges(links)에 담기며 $E$로 표기한다.
• node와 edge로 이루어진 전체 system을 graph 혹은 network라고 하며 $G(N,E)$로 표기한다.

Directions & Node Degrees

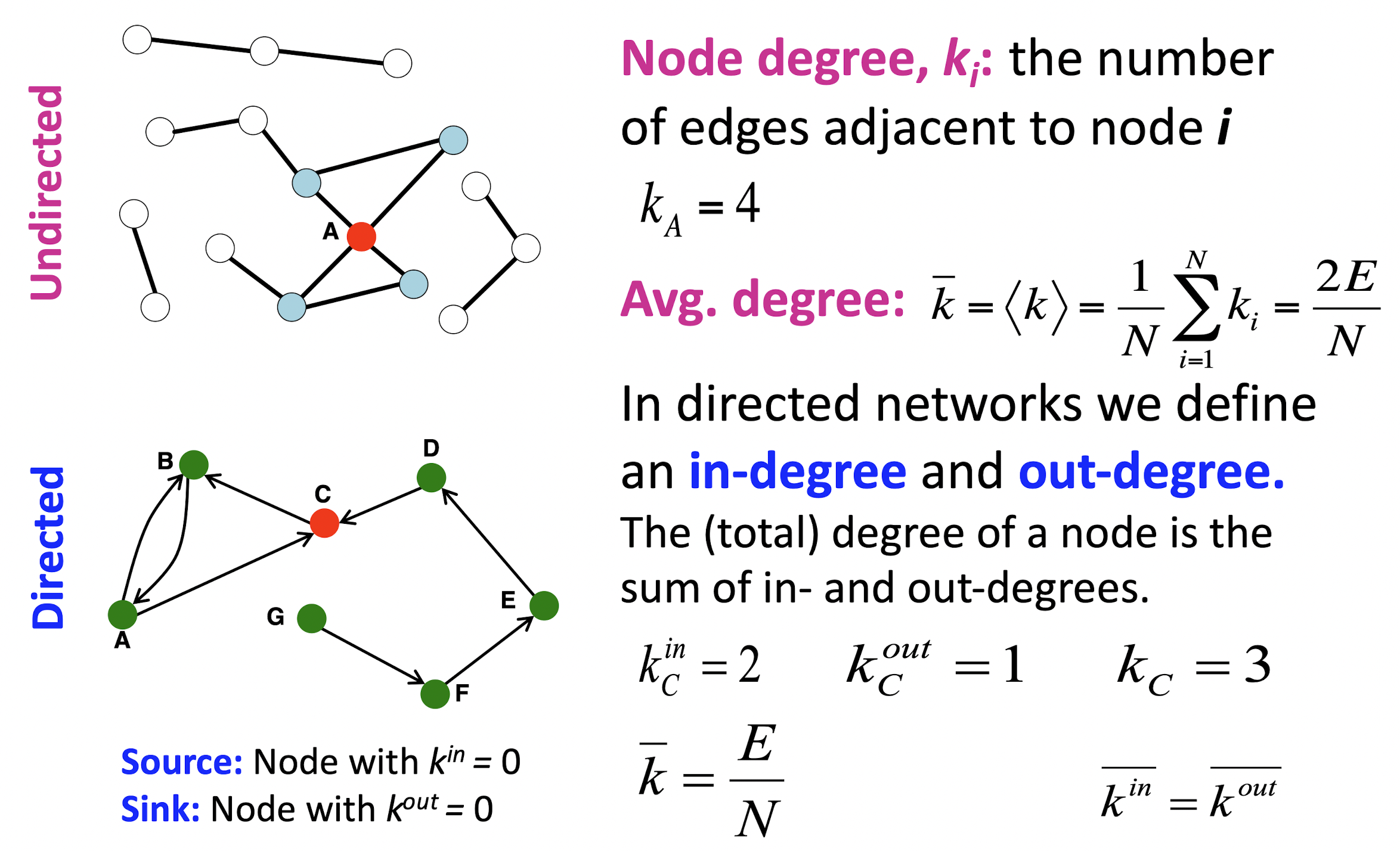
• 양방향 그래프를 Undirected graph라 하며 friendship, collaborations와 같은 관계를 표현할 수 있다.
• 일방향 그래프를 Directed graph라 하며 following, phone calls와 같은 관계를 표현할 수 있다.
• $i$번째 노드의 인접 엣지의 수를 $k_i$로 표기하면 Undirected graph의 평균 $\bar{k}=\frac{1}{N} \sum_{i=1}^{N} k_{i}=\frac{2 E}{N}$가 된다.
• Directed graph의 경우 방향성이 있어 $k_i^{in}$과 $k_i^{out}$으로 나뉘며 평균은 in, out 모두 $\bar{k}=\frac{E}{N}$로 같다.

Bipartite Graph

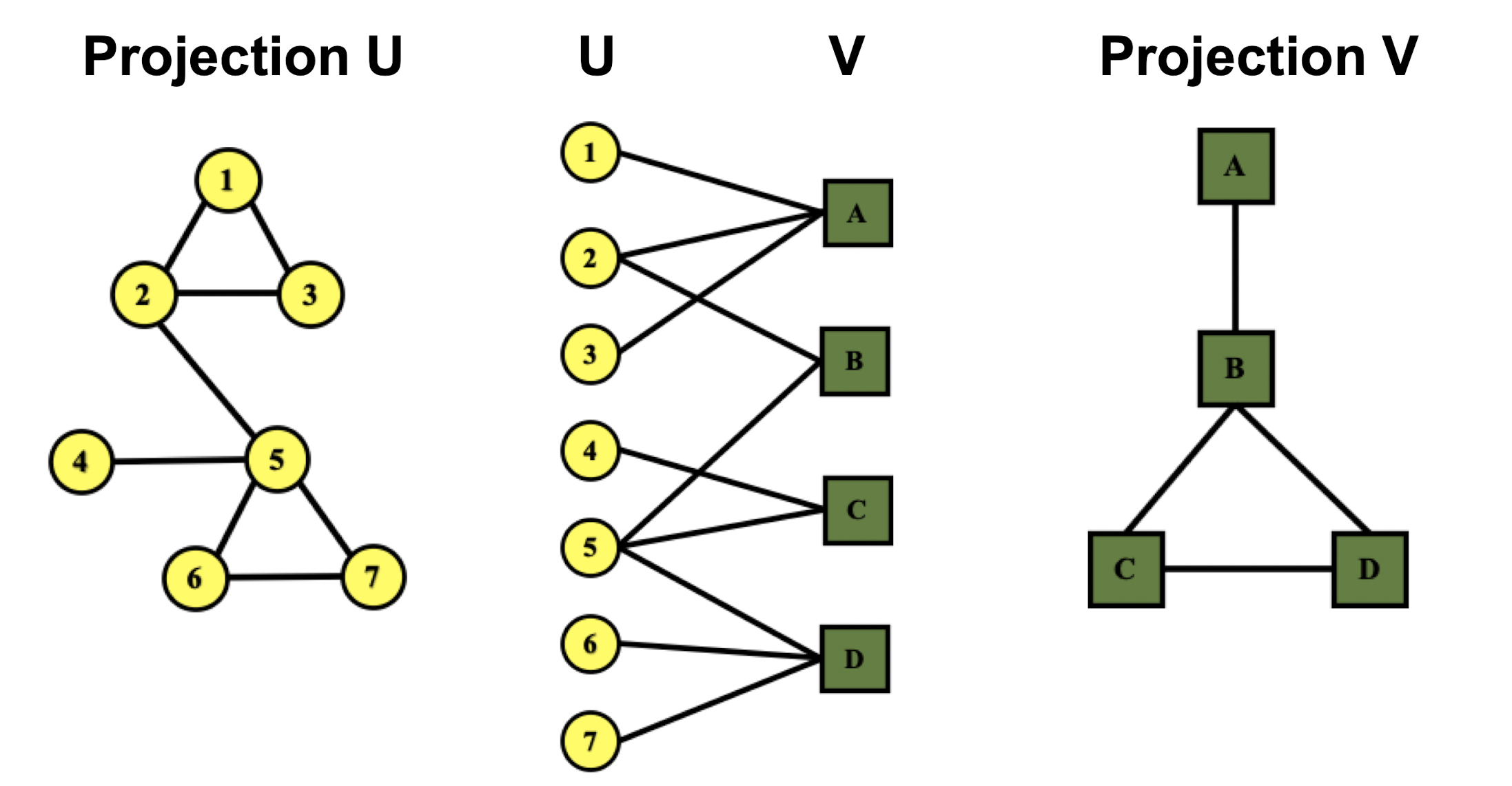
• Biparitite graph는 독립적인 두 개의 set인 $U, V$로 구성된 그래프로 각 set의 노드들끼리는 독립적이며 다른 set와의 연관성만 가진다.
• Authors-to-Papers, Actors-to-Movies 등이 그 예시가 될 수 있다.
• 다른 세트의 동일한 노드와 연결된 노드들끼리 연결시켜 $Projection U,V$를 만들 수 있다.

Graph representation

Adjacency Matrix

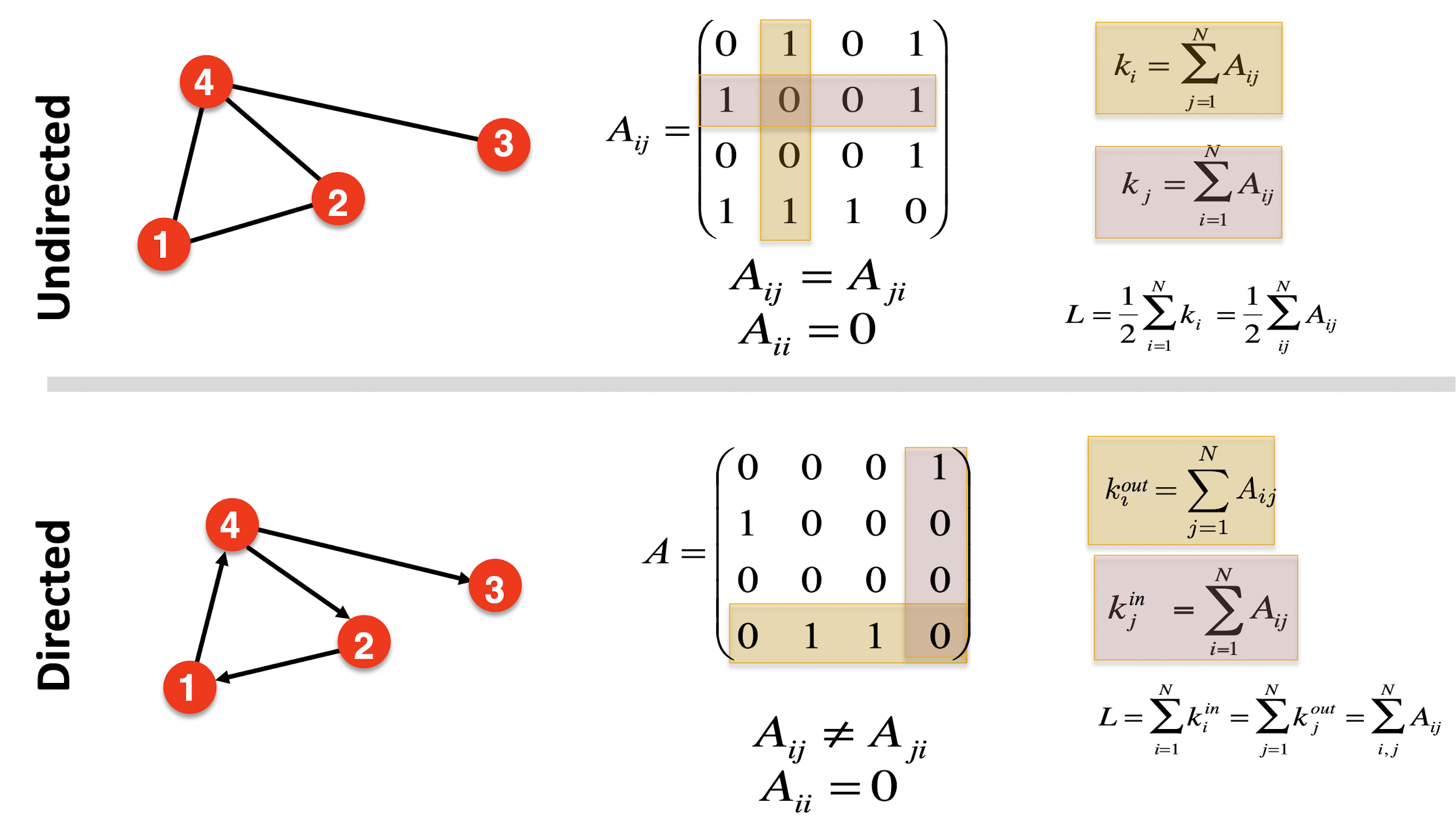
• $i$번째 노드와 $j$번째 노드가 연결되어 있을 때 1, 연결되지 않았을 때 0으로 표시하여 인접행렬을 만들 수 있다.
• Undirected graph의 경우 $A_{i j}=A_{j i}$이므로 symmetric하며 Directed graph에서는 성립하지 않는다.
• 엣지의 수 $L$은 Undirected graph에서는 $\frac{1}{2} \sum_{i j}^{N} A_{i j}$, Directed graph에서는 $\sum_{i, j}^{N} A_{i j}$이다.

Edge list

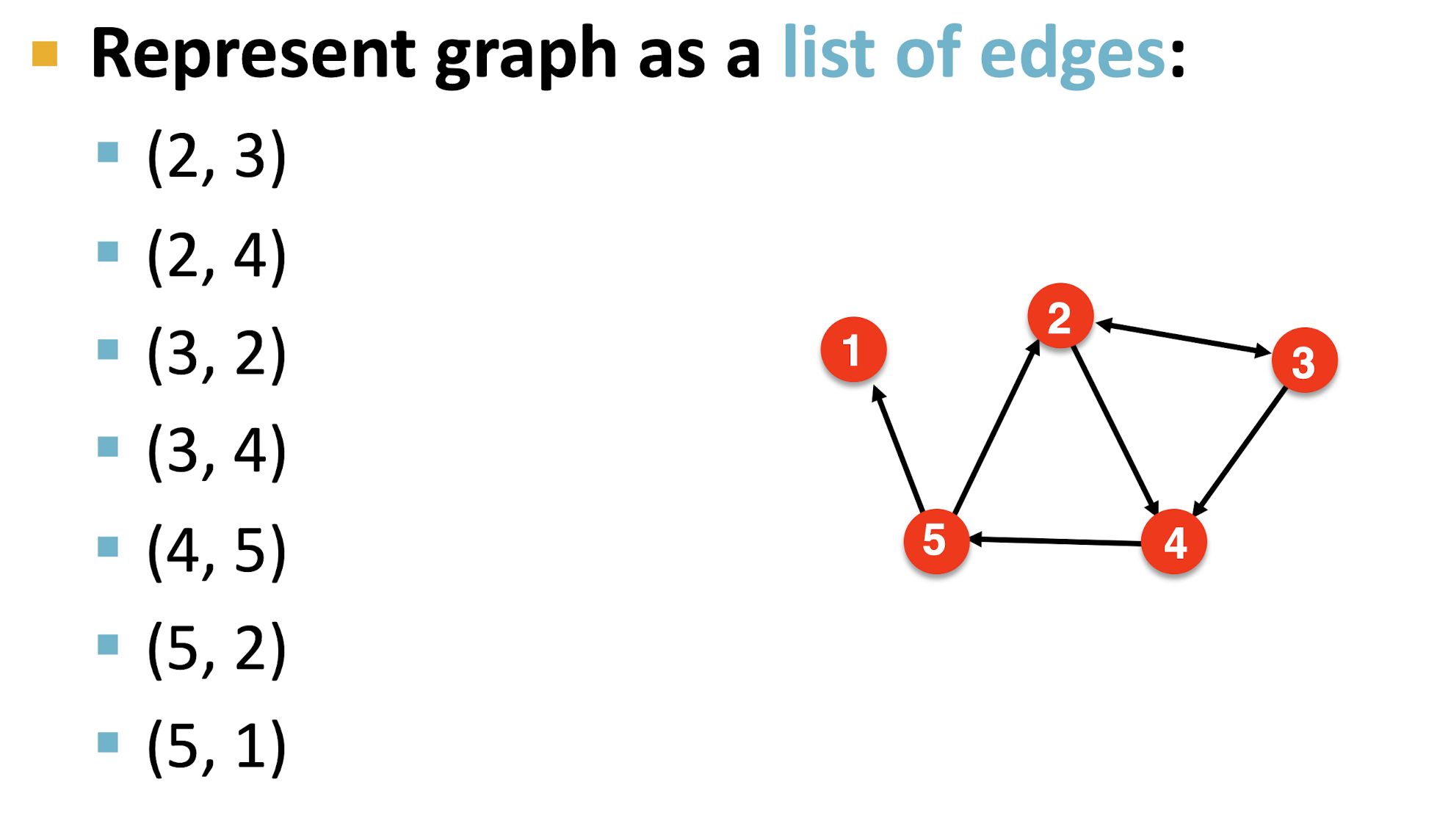
• 출발 노드와 도착 노드의 쌍으로 표현하는 방법

Adjacency list

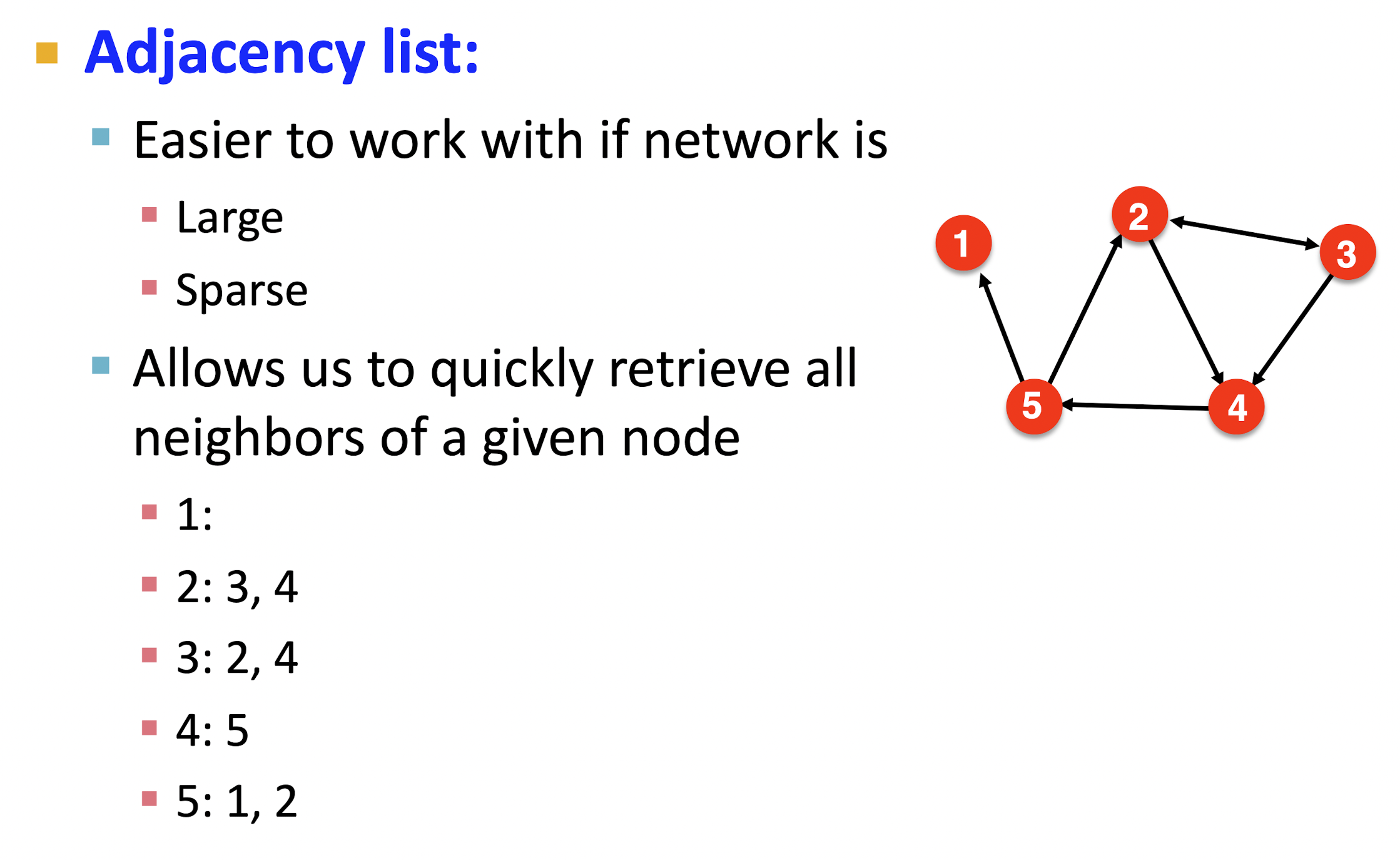
• 출발 노드를 key, 도착노드들을 values로 두어 dictionary 형태로 표현하는 방법

More Types of Graphs

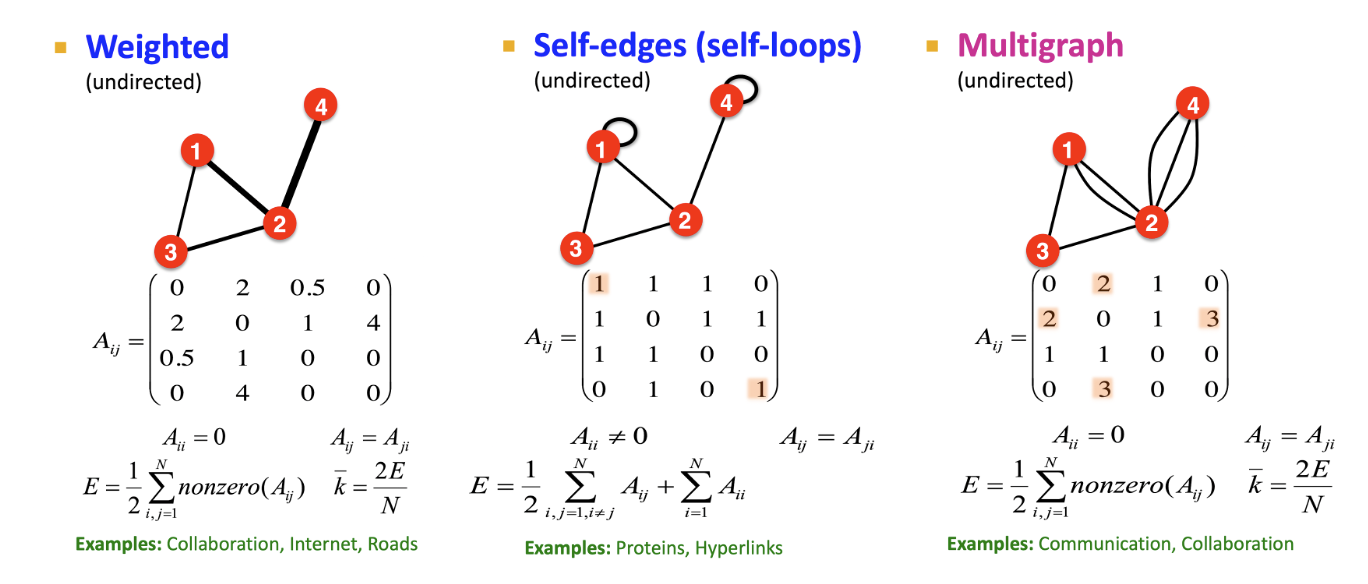
• 엣지에 가중치가 있는 Weighted graph, 자기 자신으로의 엣지가 있는 Self-loops graph, 2개의 노드를 있는 엣지가 2개 이상인 Multigraph 등 다양한 형태의 그래프들이 있다.

Connectivity

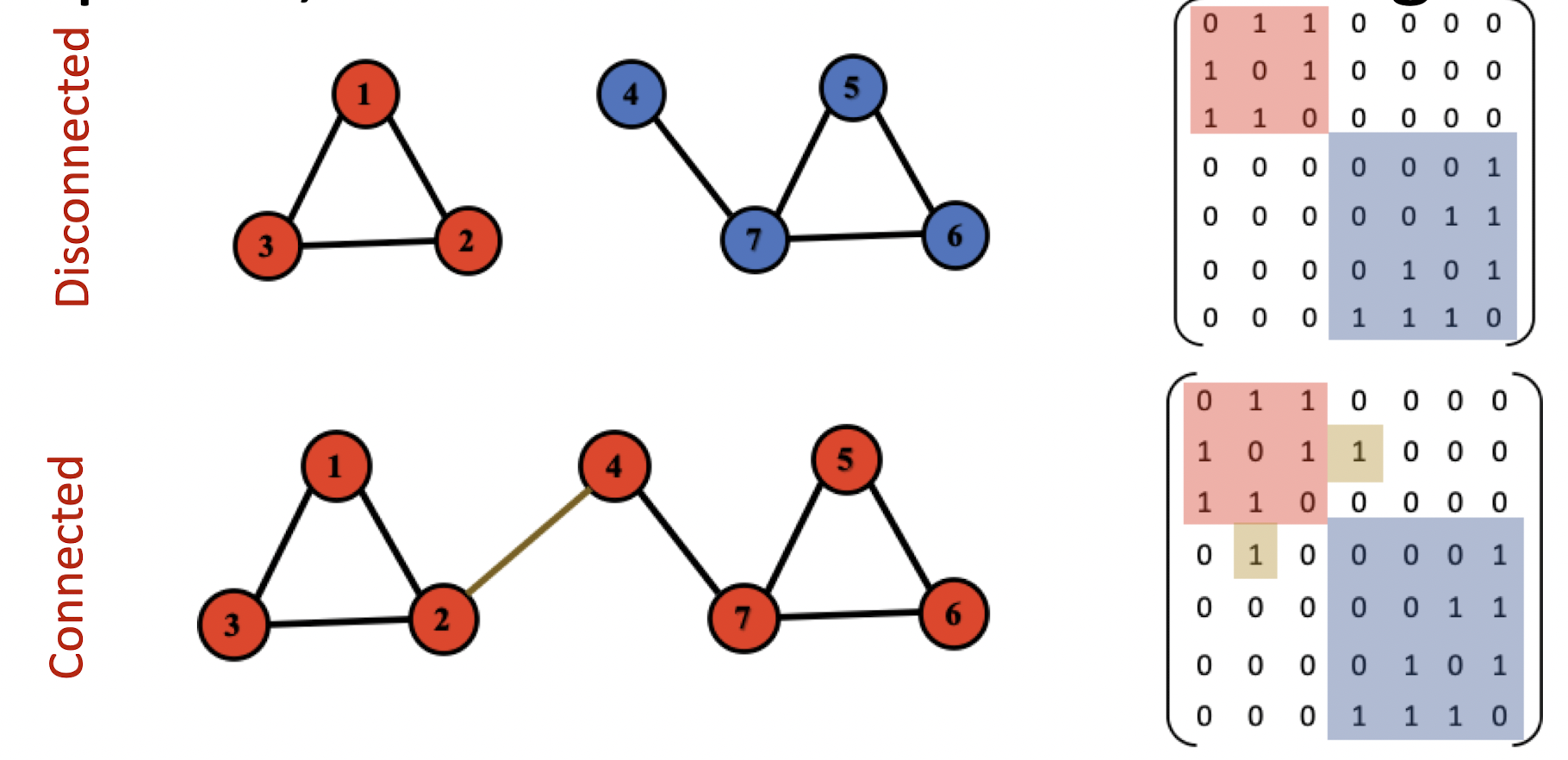
• Conntected graph(undirected): 어떤 노드에서 출발하든지 도착 노드로 갈 수 있는 그래프
• Disconnected graph: 그래프가 끊어져있어 출발 노드에 따라 못 가는 노드가 생기는 그래프
• Bridge edge: 삭제될 경우 Disconnected graph로 만드는 edge
• Articulation node: 삭제될 경우 Disconnected graph로 만드는 edge
• Disconnected graph의 인접행렬은 block-diagonal 형태이다.

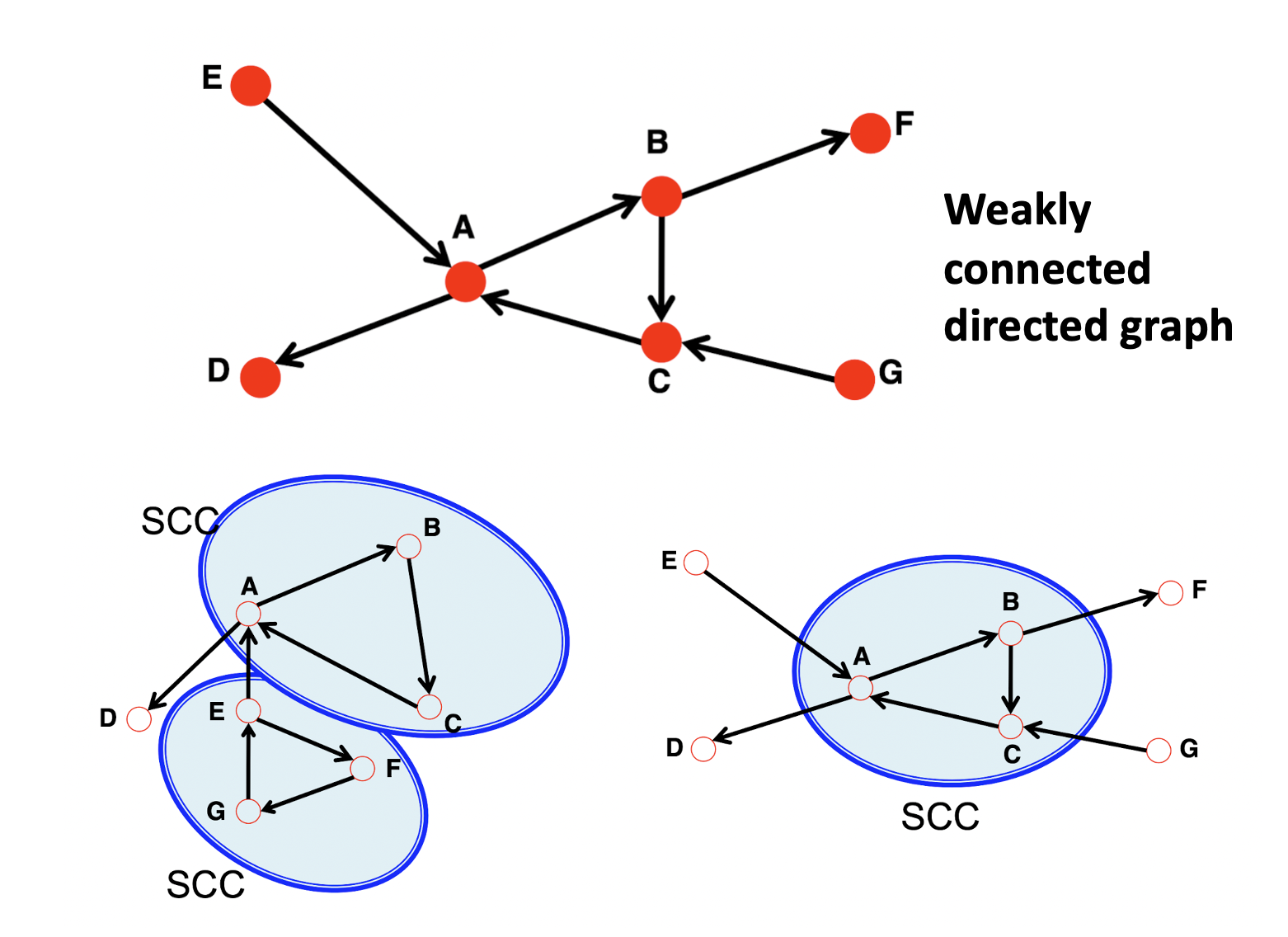
• Strongly connected directed graphh: edge의 방향과 상관없이 A->B, B->A의 길이 모두 연결되어있는 그래프.
• Weakly connected directed graph: 노드들이 전부 연결되어 있지만 방향에 의해 다른 노드로 못 가는 경우가 있는 그래프. 예를 들어, 위 그래프에서 F->G의 길은 존재하지 않는다.
• SSC(Strongly connected components): 그래프 내에서 부분적으로 strongly connected된 subgraph.

Reference

• https://www.youtube.com/watch?v=JAB_plj2rbA&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=1