1. Node-level Tasks and Features

Node의 위치 및 구조를 파악하기 위한 feature로는 Degree, Centrality, Clustering coefficient, Graphlets가 있다.

Node Degree

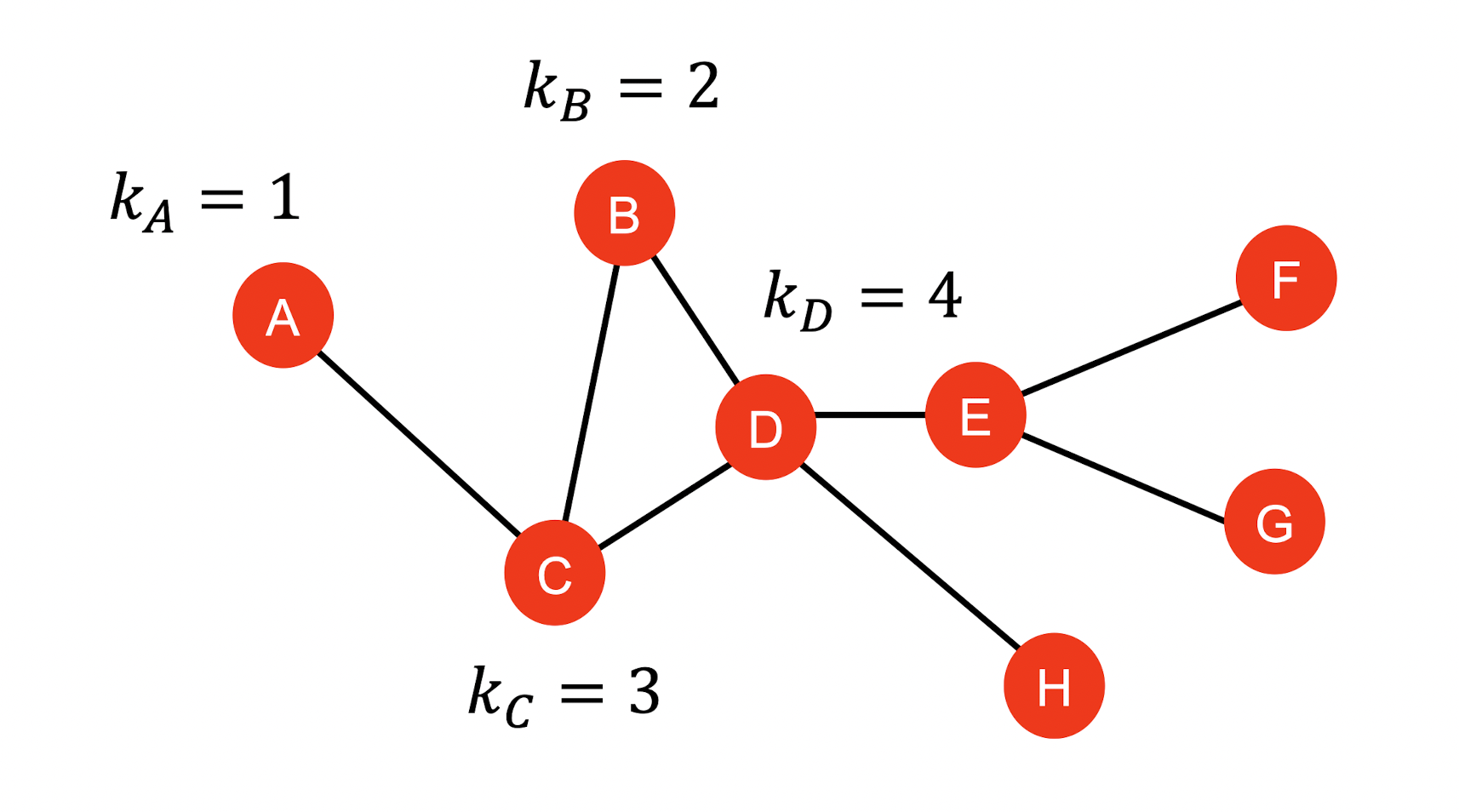
• $k_v$는 node $v$의 edge의 수를 의미한다.
• edge의 수 = 이웃 node의 수

Node Centrality

Node degree는 이웃 node의 중요성을 반영하지 않는다. 중요성을 반영하기 위해 node centrality $c_v$를 도입하며 어떤 값을 줄지에 대한 방법은 다양하다.

Eigenvector centrality

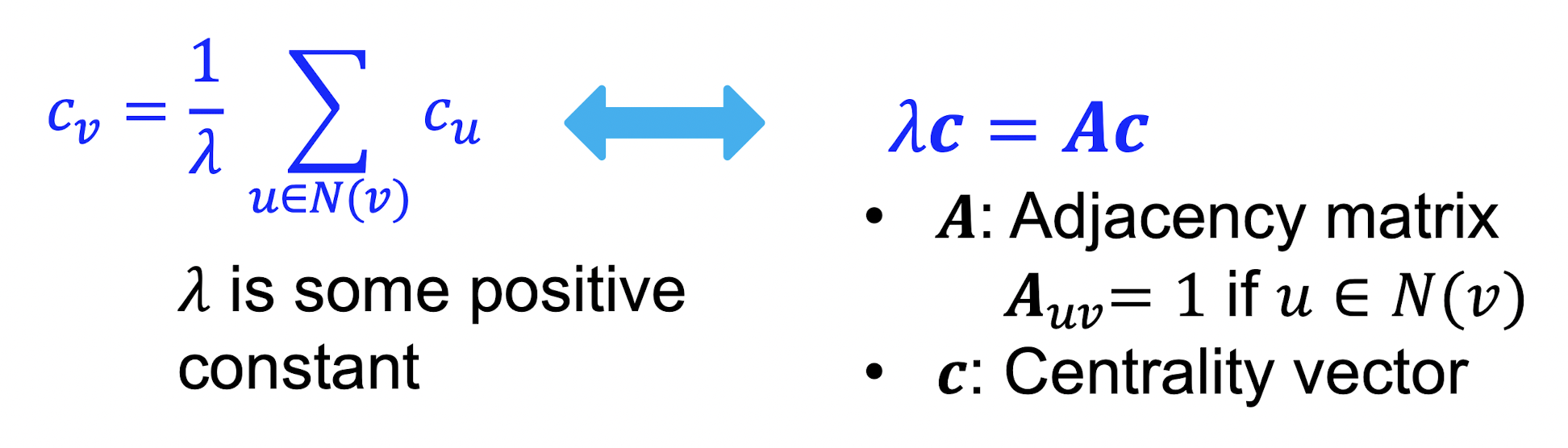
• node $v$는 중요한 이웃 node들로 둘러쌓여 있을 때 그 중요성이 크다할 수 있다.
• 따라서 node $v$의 centrality를 이웃 노드들의 centrality의 합으로 정의한다.
• 위 식은 recursive equation이며 matrix 형태로 변환할 수 있다.
• $A$는 node들 간의 관계를 나타내는 인접행렬이며 $c$는 Centrality vector이므로 $c$가 eigenvector임을 알 수 있다.

Betweenness centrality

• 어떤 node가 다른 node들의 shortest path를 연결해주는 징검다리 역할을 한다면 중요성이 크다고 할 수 있다.
• node $s$와 $v$를 잇는 모든 shortest path 중 node $v$를 거치는 경우의 비율을 $c_v$로 정의한다.

Closeness centrality

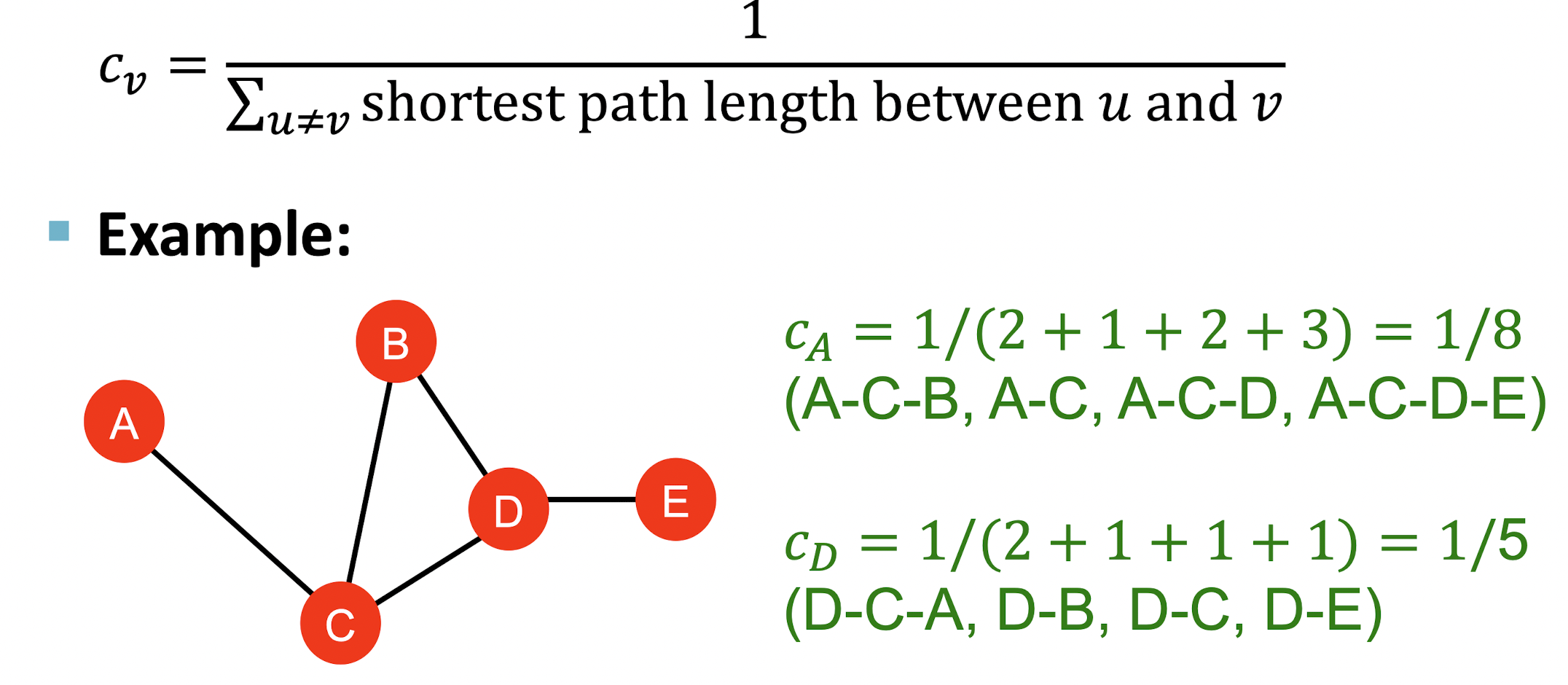
• 다른 node들과의 거리가 짧을 경우 그 node는 중요성이 크다고 볼 수 있다.
• 모든 node로 가는 shortest path의 길이의 역수로 $c_v$를 정의한다.

Clustering Coefficient

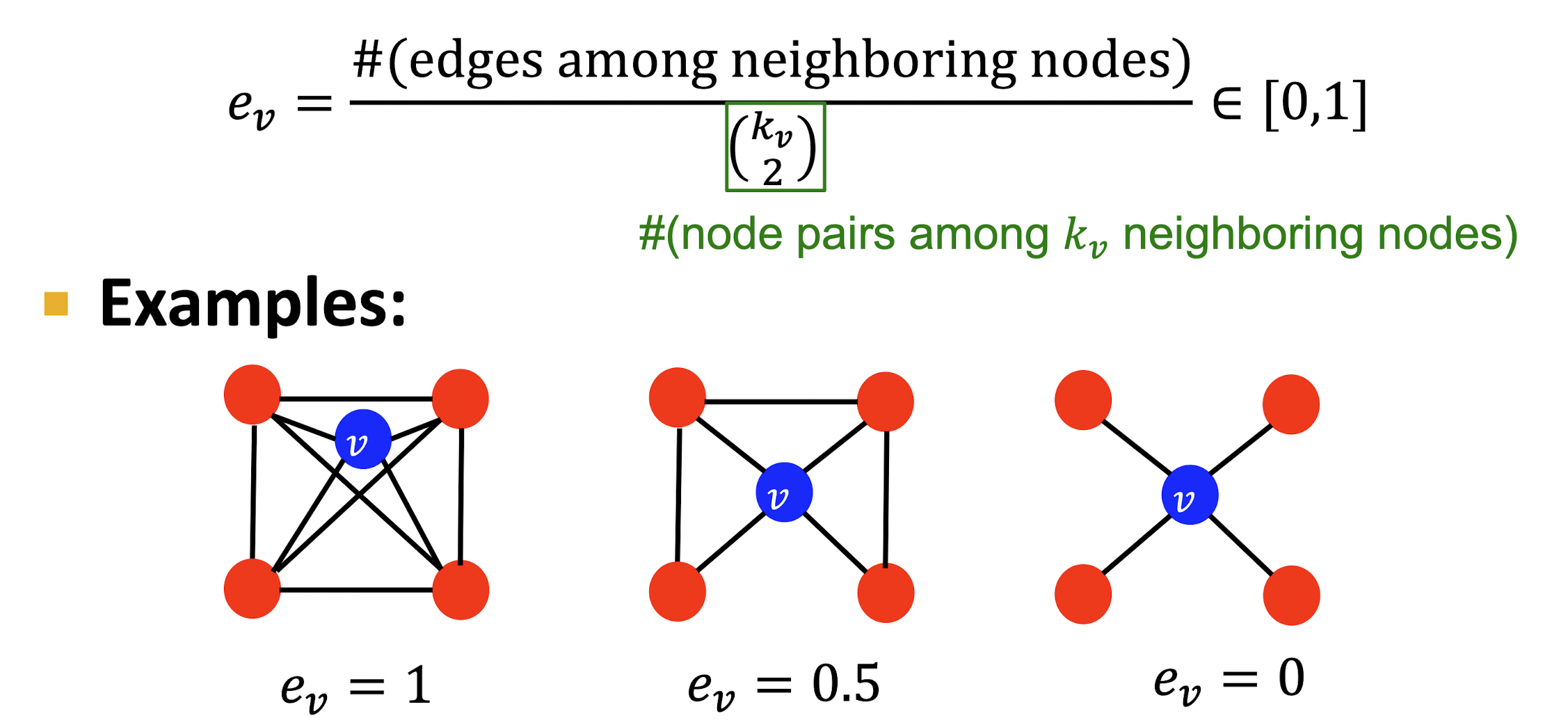
• 이웃 node들 간의 연결성을 나타내는 계수로 그 값이 높을수록 clusetring 되어 있다고 볼 수 있다.
• $k_v$개의 이웃 node의 최대 연결 가능 edge의 수 $\left(\begin{array}{c} k_{v} \\ 2 \end{array}\right)$ 중 실제 연결된 edge의 수의 비율로 $e_v$를 정의한다.

Graphlets

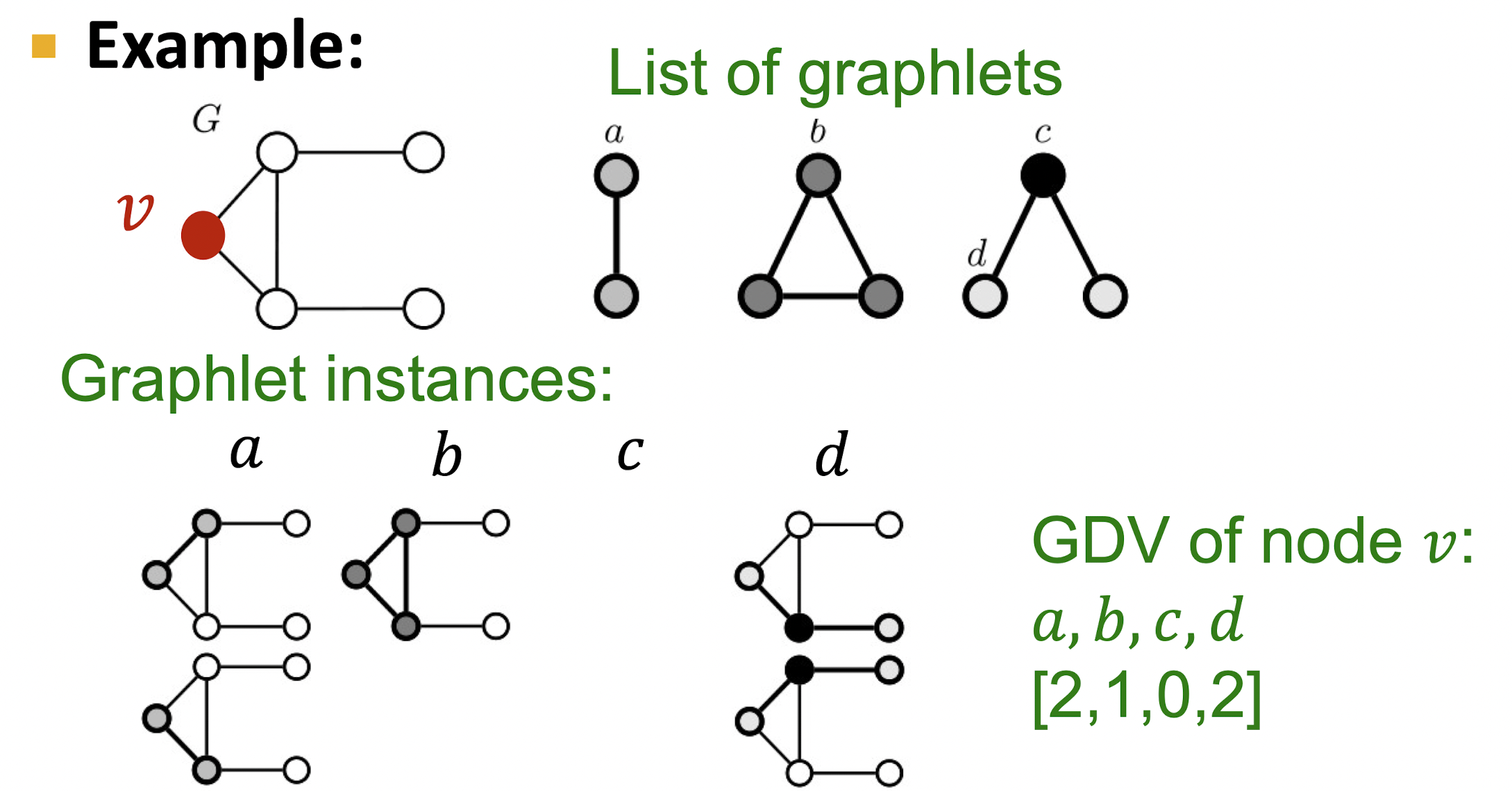
• non-isomorphic subgraphs로 주어진 node를 특징화 할 수 있다.
• Graphlet Degree Vector(GDV)는 node의 지역적 위상을 측정해주는 척도로 두 node의 비교는 그 node의 주변이 얼마나 비슷한지를 나타낸다.
• node $v$를 root로 할 때 $a,b,c,d$가 root인 subgraph와 동일한 모양을 가지는 경우의 수를 벡터 형태로 담아 GDV를 나타낸다.

2.Link Prediction Task and Features

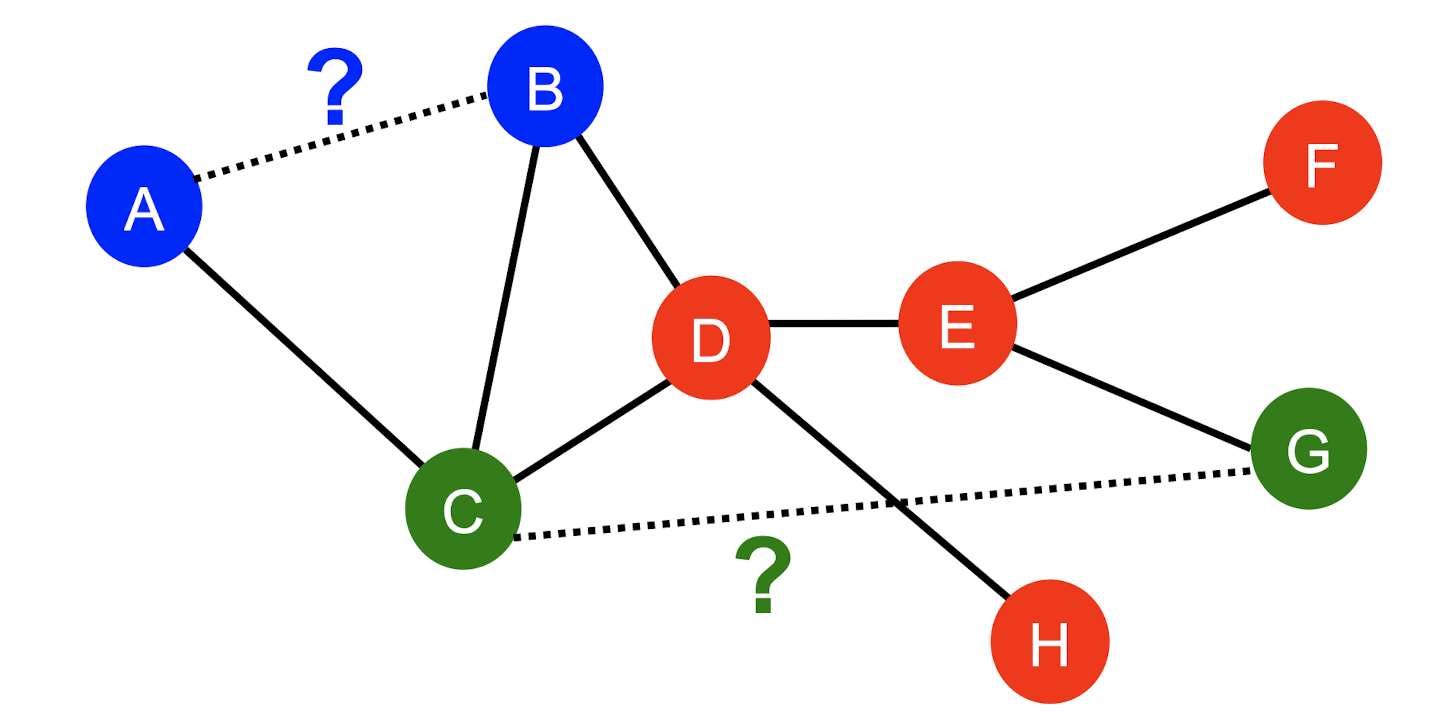
• 기존의 edges에 기반하여 새로운 edges를 예측
• node쌍의 feature를 design하는 것이 핵심이다.
• Link-level features로는 Distance-based feature, Local neighborhood overlap, Global neighborhood overlap이 있다.

  Link Prediction Task

  1. Edge들을 무작위로 삭제한다.
  2. $G[t_0,t_0']$로부터 두 node의 score $c(x,y)$를 계산하여 내림차순으로 정렬한 뒤 상위 n개의 새로운 edge들을 예측한다.
  3. $G[t_1,t_1']$에서 실제로 나타나는 edge들인지 비교하여 evaluation한다.

Distance-Based Features

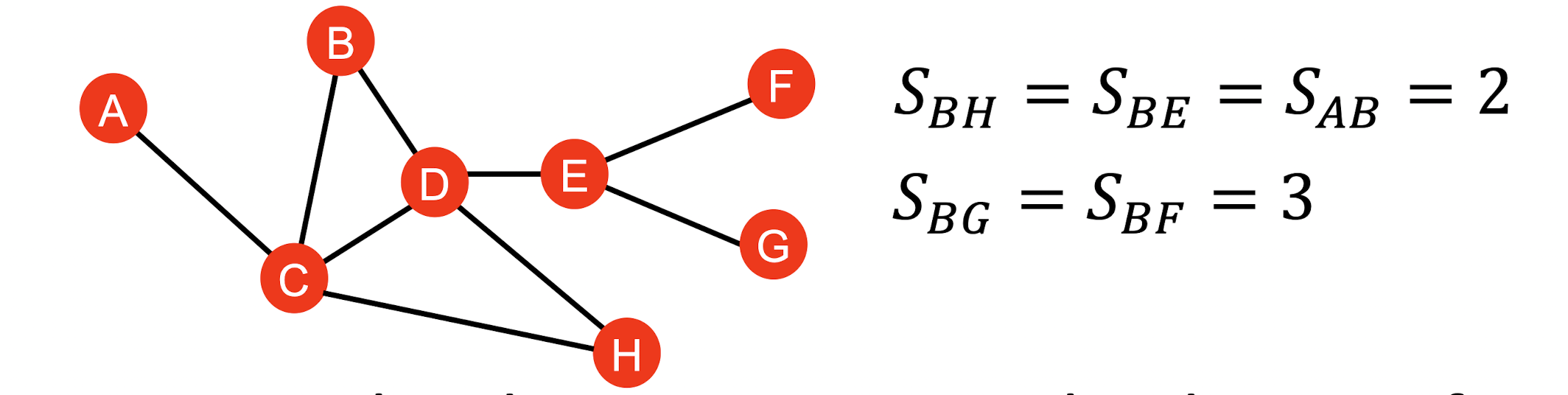
• 두 node 간의 최단거리를 feature로 둔다.

Local Neighborhood Overlap

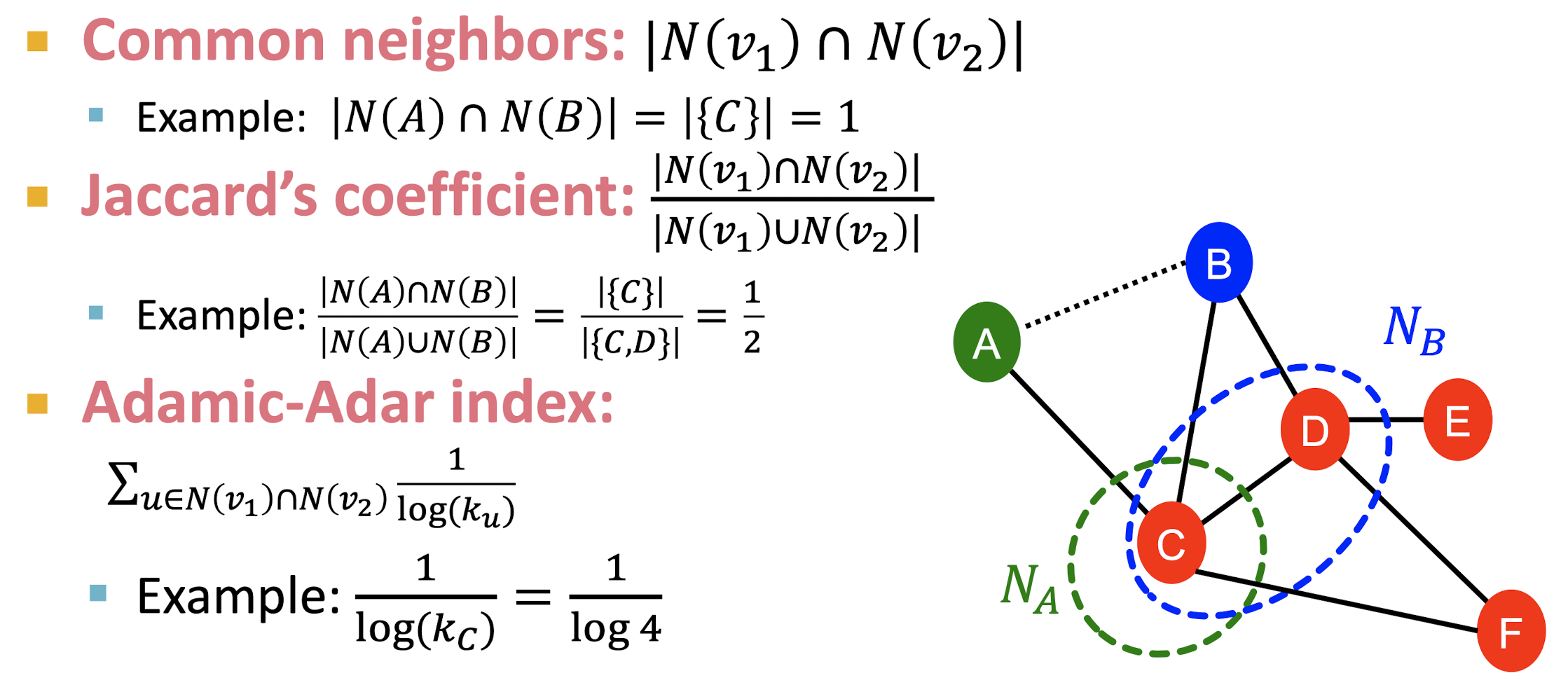
• 두 node가 공유하는 neighbor nodes를 feature로 둔다.
• Common neighbors는 두 node가 공유하는 neighbor node의 수를 의미한다.
• Jaccard's coeeficient는 두 node의 모든 neighbor nodes 중 공유하는 node의 수의 비율을 의미한다.
• Adamic-Adar index는 두 node가 공유하는 node의 neighbor nodes의 수에 역수를 취하는 값으로 공유하는 node가 많다 하더라도 degree가 크다면 두 node의 연관성이 떨어질 수 있음을 나타내기 위해 쓰인다.

Global Neighborhood Overlap

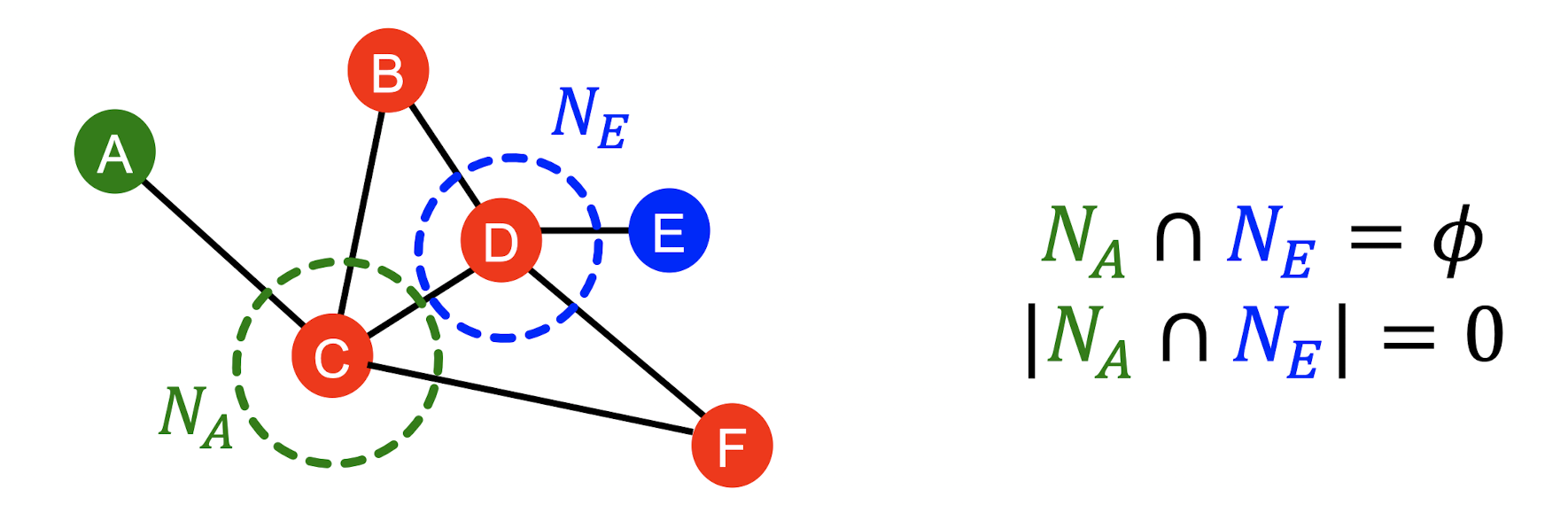
• 위 그래프에서 $A$와 $E$는 공유 node가 없으므로 metric이 0이 된다.
• 하지만 두 node 또한 연결될 수 있는 potential이 존재한다.
• 따라서, 두 node의 모든 path를 세는 Katz index를 활용한다.
  
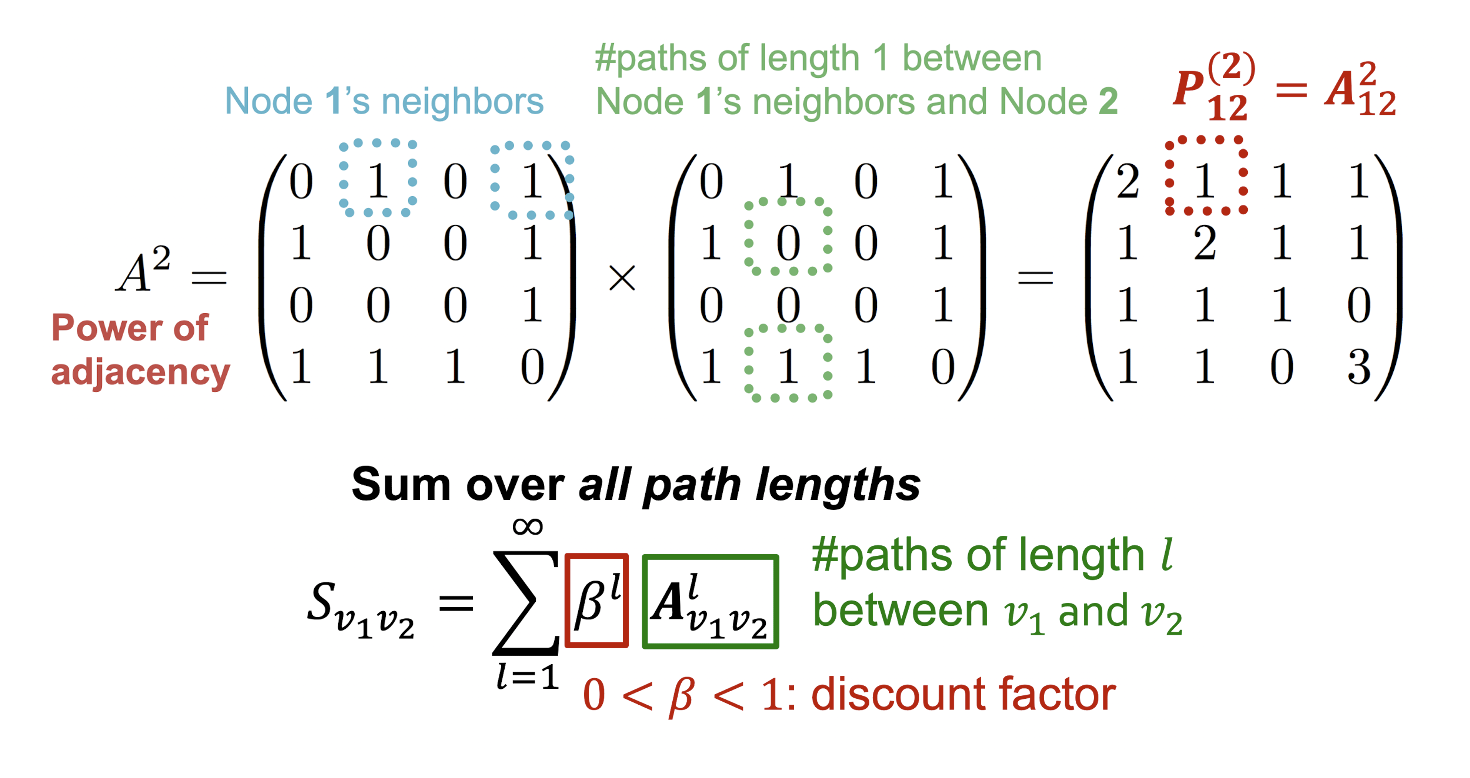
• $A^l_{v_1v_2}$은 두 node $v_1,v_2$의 length가 $l$인 path의 개수를 의미하므로 $S_{v_1v_2}$를 통해 Katz index를 구할 수 있다.

3. Graph-Level Features

• Graph 구조에 대한 feature를 얻기 위해 커널을 활용할 수 있다.
• 커널 $K(G,G') \in \mathbb{R}$가 그래프 간의 유사도를 측정한다고 할 때 feature represenstation을 얻을 수 있다.
  $K(G,G') = \phi(G)^\top \phi(G')$
• Graph Kernerl에는 Graphlet Kernel, Weisfeiler-Lehman Kernel 등이 있다.

Bag of Words(BoW)

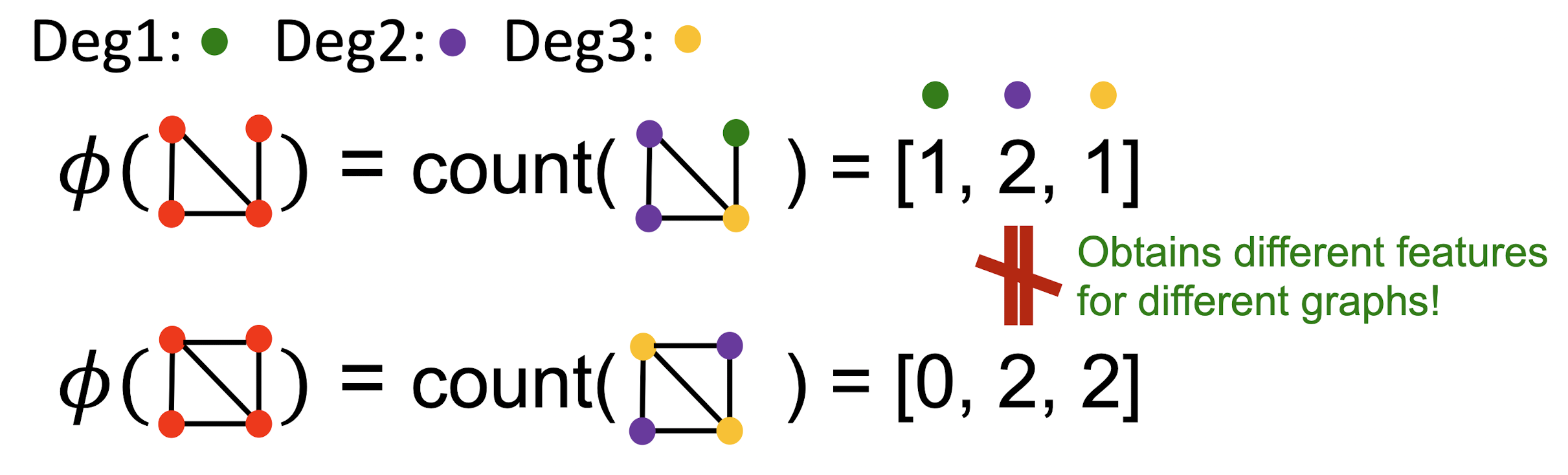
• NLP에서 document 내에서 나타나는 word의 수를 세는 표현방식을 그래프에도 적용할 수 있다.
• 위 그래프에서 두 그래프가 동일하게 4개의 node를 가지므로 같은 크기의 feature vector를 얻을 수 있으며 degree의 수에 따른 node의 개수를 벡터 형태로 기록했을 때 서로 다른 그래프임을 알 수 있다.

Graphlet Features

• 그래프 내의 다른 graphlets의 수를 세는 방식
• node-level에서의 graphlet과는 다르게 정의된다.

  

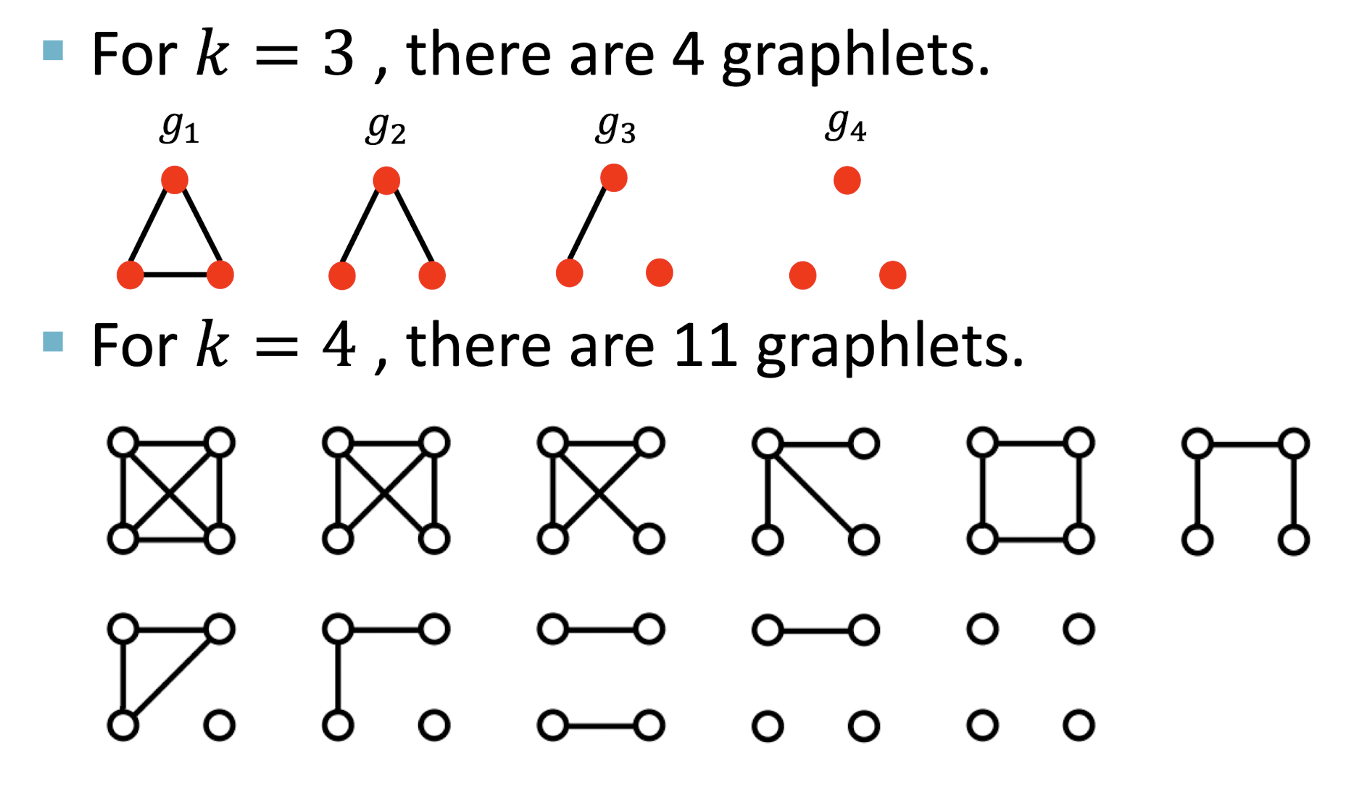
  • Graphlets의 nodes가 꼭 연결되어 있을 필요는 없다.
    ( = isolated nodes를 허용한다.)
  • Graphlets에 root가 존재하지 않는다.

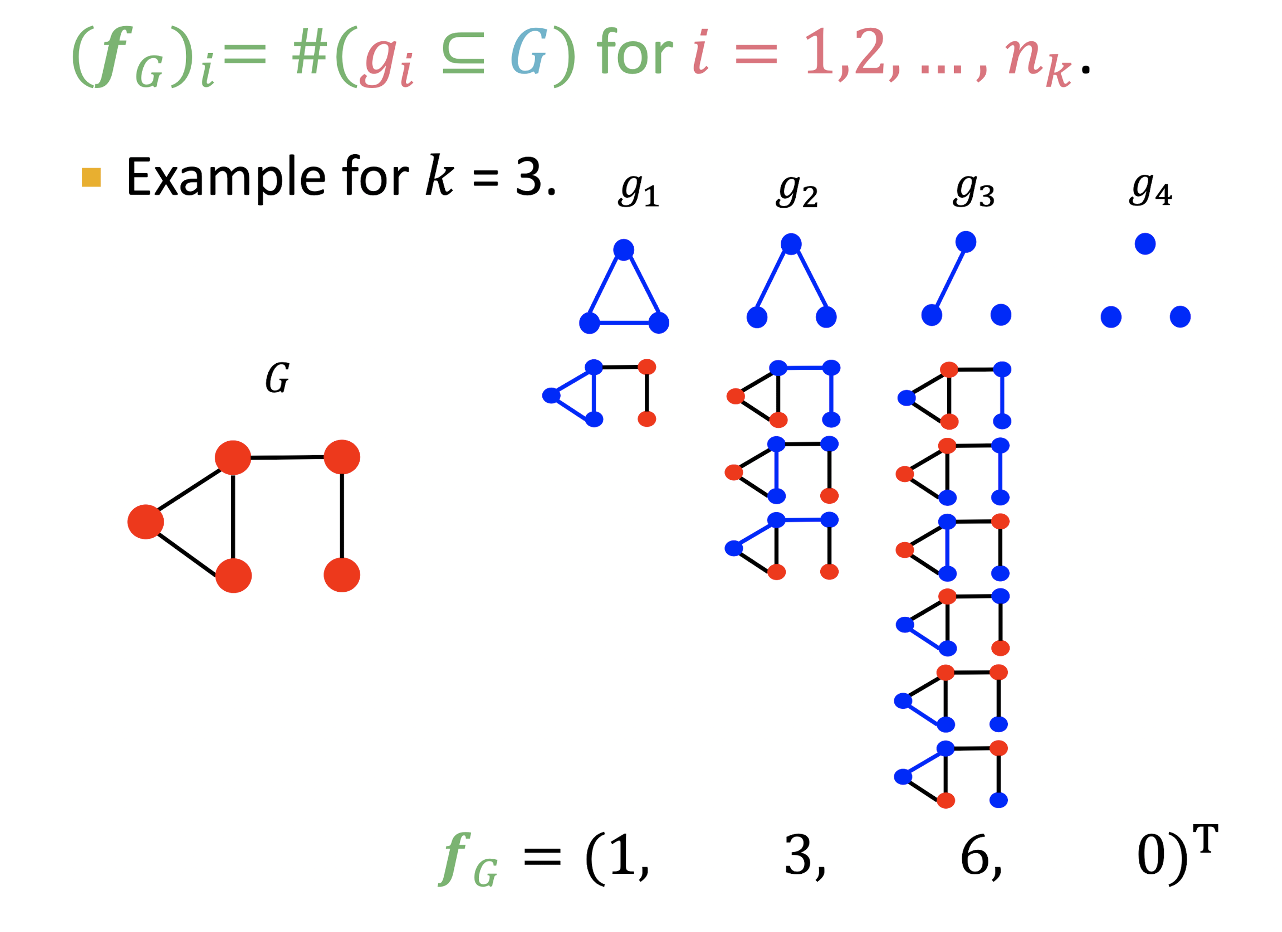
• Feature $(f_G)_i$는 그래프 $G$에 포함되는 graphlet $\mathcal{G_k}$의 개수로 표현할 수 있다.
• Graphlet을 활용하여 kernel을 $K(G,G') = f_G^\top f_{G'}$로 정의할 수 있다.
• 하지만 $G$와 $G'$가 다른 size를 가질 수 있기 때문에 정규화 된 feature vector $h_G$를 활용한다.
  

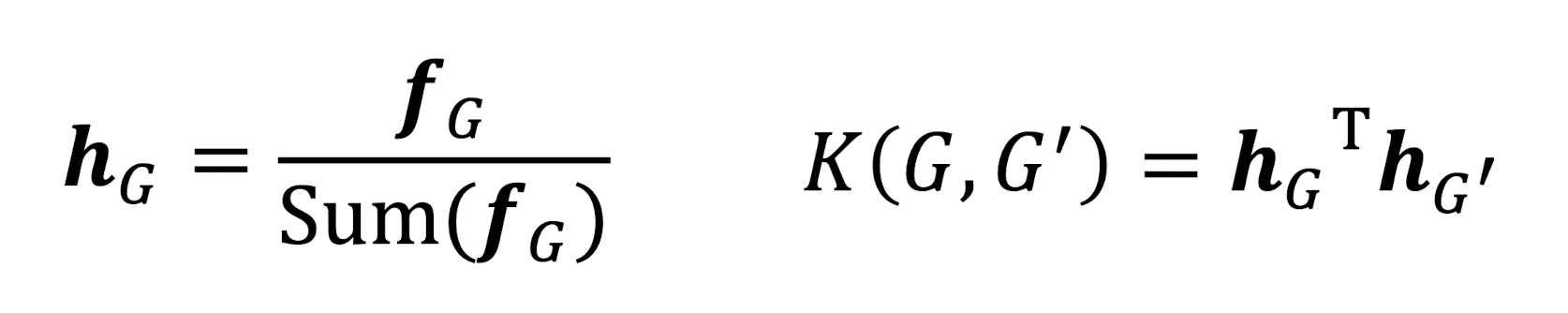
Weisfeiler-Lehman Kernel

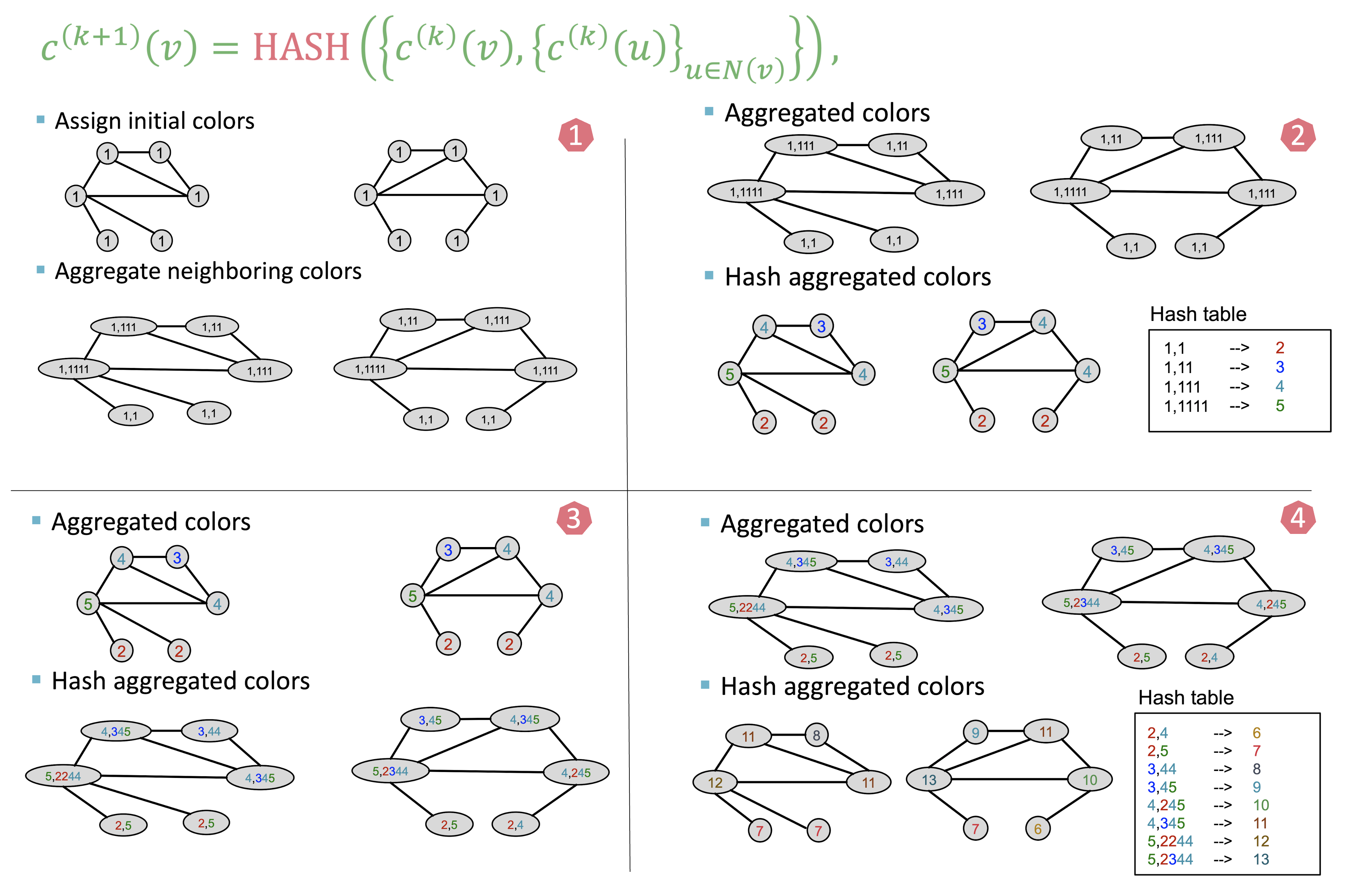
Color Refinement 과정

• 모든 노드에 초깃값을 지정한다.
• 이웃 노드들을 값을 root 노드에 덧붙인다.
• Hash table 형태로 key에 따라 value(=color)를 부여한다.
• 위의 과정을 반복한다.

• Graphlet을 활용하는 방식은 계산량이 많아 color refinement를 활용한다.
• 각 color를 가지는 노드의 수를 vector 형태로 담아 feature vector $\phi$를 도출할 수 있으며 $\phi(G_i)^\top \phi(G_j)$로 두 그래프의 유사도를 구할 수 있다.
• 각 스텝에서 WL kernel의 시간복잡도는 엣지의 수에 linear하다.

References

• Lecture2.1: https://www.youtube.com/watch?v=3IS7UhNMQ3U&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=4
• Lecture2.2: https://www.youtube.com/watch?v=4dVwlE9jYxY&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=5
• Lecture2.3: https://www.youtube.com/watch?v=buzsHTa4Hgs&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=6