Overview
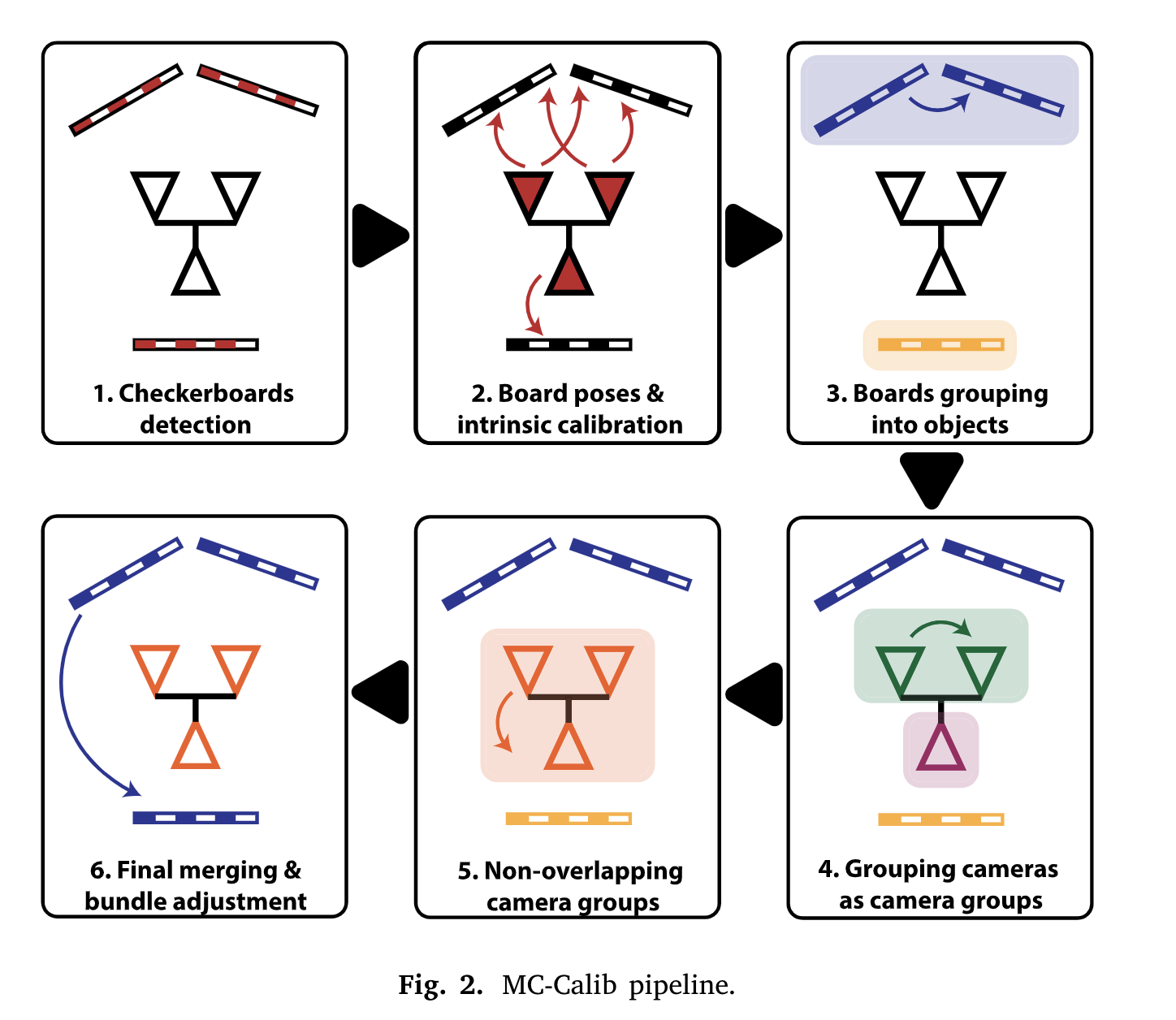
- Charuco board detection을 통해 모든 카메라의 intrinsic parameter initialization
- N-point technique을 통해 관측되는 board에 대한 camera pose에 대해 추정
- Single image에서 보이는 board 간의 transformation 계산 후 merge(=3D object)
- 유사한 3D objects를 보는 카메라들을 그룹화
- Non-overlapping camera group 간의 calibration
Checkerboard detection and keypoints extraction
- 복작합 세팅을 다루기 위해 charuco board를 사용한다.
- 모든 카메라는 2D keypoints와 그에 상응하는 3D points를 저장한다.
- 이 과정이 robust해야 calibraion이 잘 이루어질 수 있으므로 corner refinement 과정을 거치며 collinearity check를 적용하고 볼 수 있는 keypoints가 threshold 미만일 때 해당 board는 무시한다.
Intrinsic parameters initialization
- 체커보드로부터 얻은 3D-2D 매칭쌍은 intrinsic parameter 와 distortion coefficient 를 초기화하기 위해 사용된다.
- Perspective camera에 대해서는 Brown distortion model을, fisheye camera에 대해서는 Kannalla distortion model을 사용한다.
- 위 방식들은 image가 많을 때 상대적으로 느려 카메라 당 50개의 image를 subsampling 한다.(이후 refinement 시에는 모든 image 사용)
- Non-ovelapping camera가 많을 때 다양한 viewpoints에 대한 정확한 intrinsic calibration을 하는 것은 비효율적이기 때문에 pre-computed intrinsic parameter를 사용할 수도 있다.
Board pose estimation and intrinsic refinement
-
관측된 board에 대한 모든 카메라의 상대적인 pose를 추정한다.
-
RANSAC을 통해 오차가 큰 outlier는 제거하며 PnP 알고리즘을 통해 와 를 구한다.
-
Inlier points는 Levenberg-Marquardt non-linear refinement에서 사용되어 board에 대한 camera의 pose를 조정하는데 활용된다.
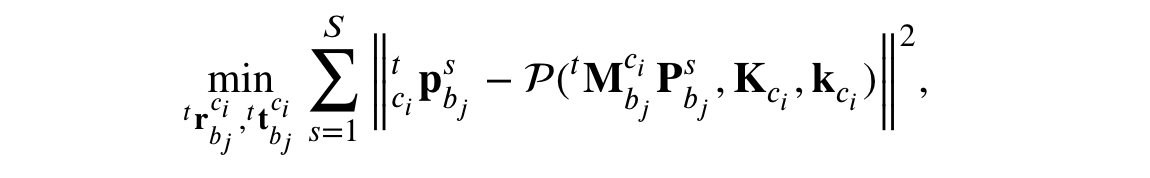
-
위와 같은 reprojection error를 통해 refine 되며 는 board에서 보이는 corner의 수를 의미한다.
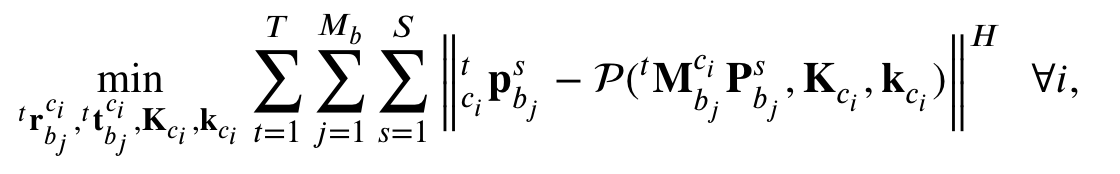
-
Intrinsic, extrinsic parameter에 대한 초깃값을 얻은 뒤에는 위와 같은 cost function을 통해 두 파라미터를 함께 refinement 한다.
-
와 는 각각 번째 카메라에서 관측되는 프레임의 수와 board의 수를 의미한다.
-
는 Huber loss로 outlier에 대한 robustness를 가지기 위해 사용한다.
Board grouping into objects
- Board들을 하나의 3D object로 합치기 위해 boards 간의 상대적인 pose를 알아야한다.
- 이는 카메라와의 pose로부터 구할 수 있다.
- Robustness를 위해 board 쌍이 함께 보이는 모든 이미지로부터 측정한 rotation, translation 값을 평균내어 계산한다.
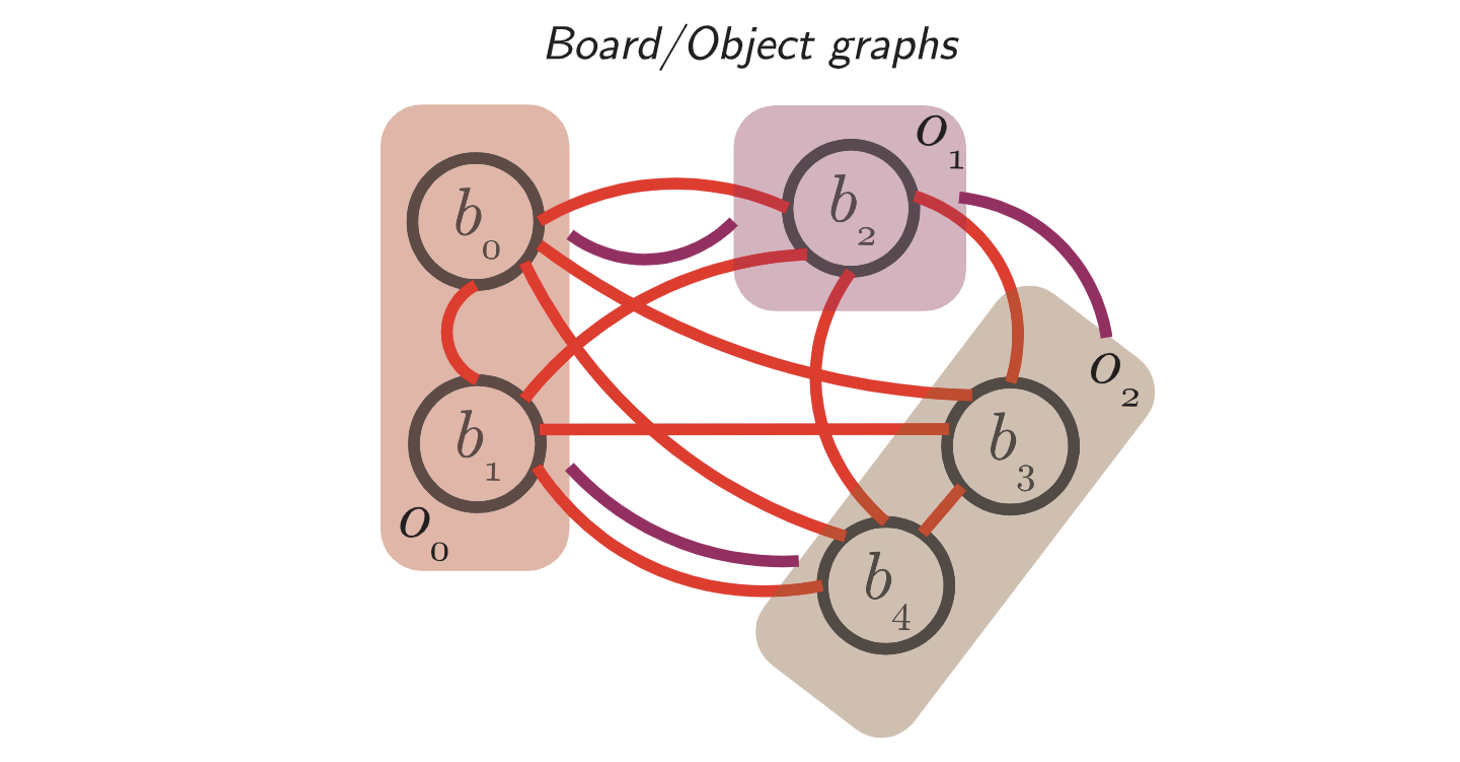
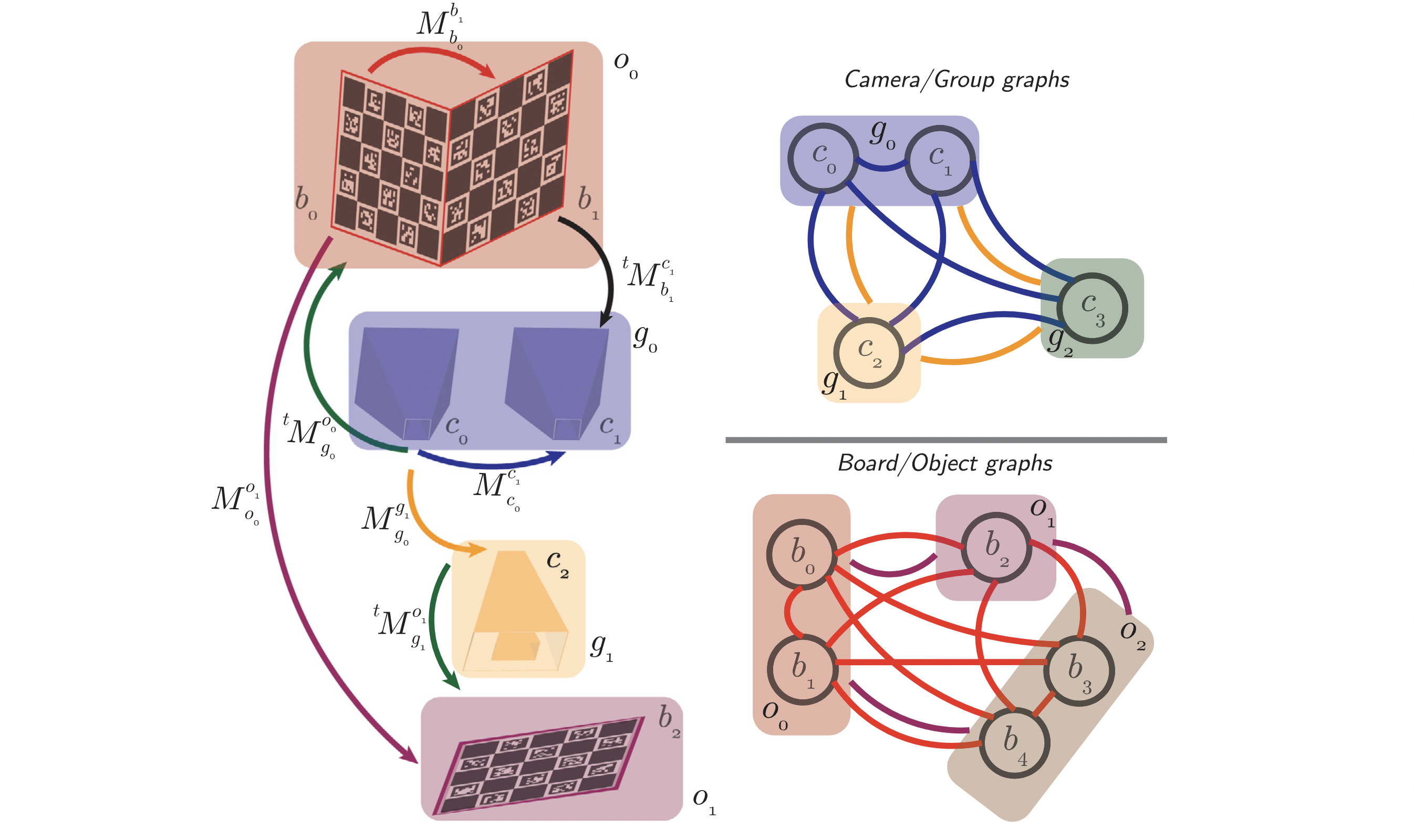
- Directed weighted graph를 활용해 inter-board poses로부터 3D object를 구성한다.
- 각 object에서의 reference board는 index가 가장 작은 board가 된다. 예를 들어 에서는 이, 에서는 이 reference board가 된다.
- 따라서, object 내에서 번째 board에 대한 pose는 로 나타낸다
-> 모든 board를 reference board의 좌표계에서 표현 할 수 있다. - Object 내에 board가 3개 이상인 경우에는 다익스트라 알고리즘을 통해 최적의 transformation 구성을 찾는다.
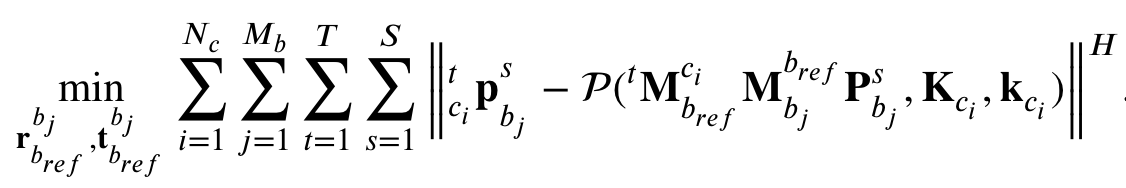
- 최종적으로 위와 같은 reprojection error를 통해 3D structure를 refinement 한다.
Extra study
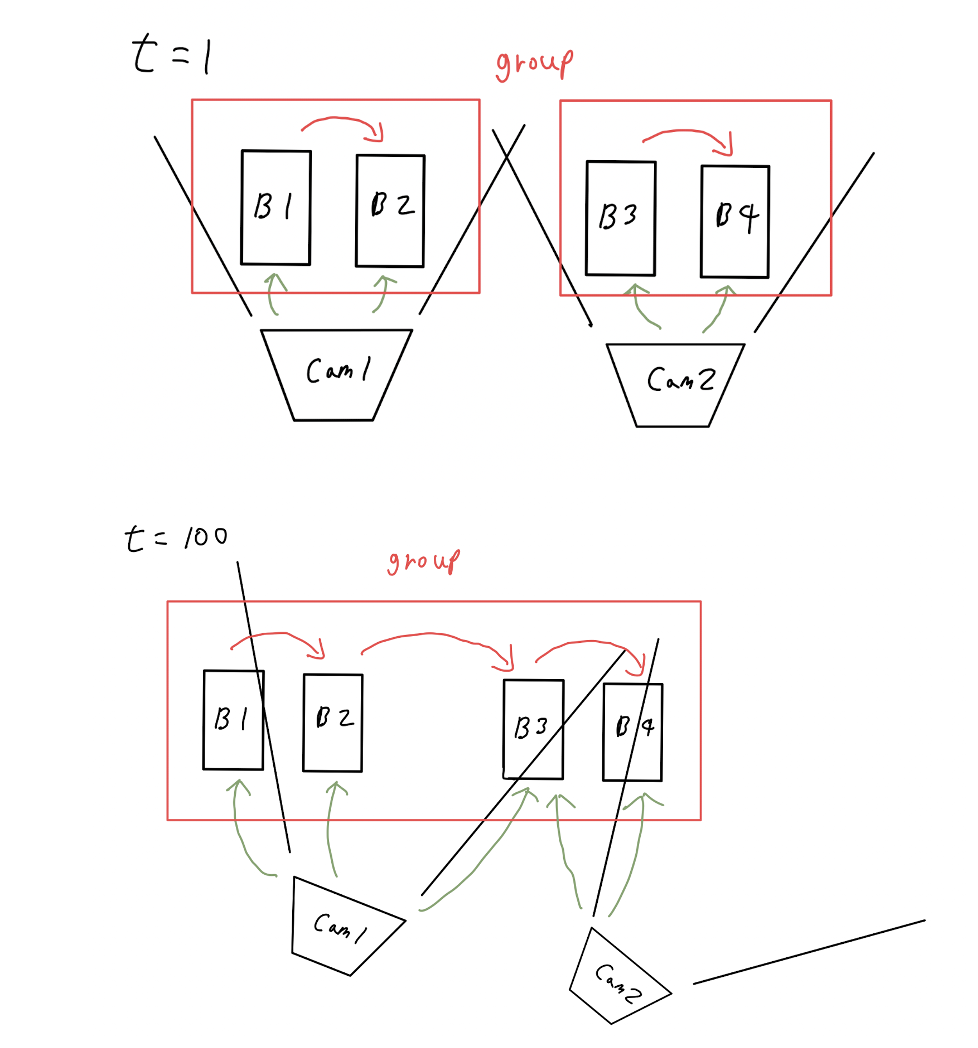
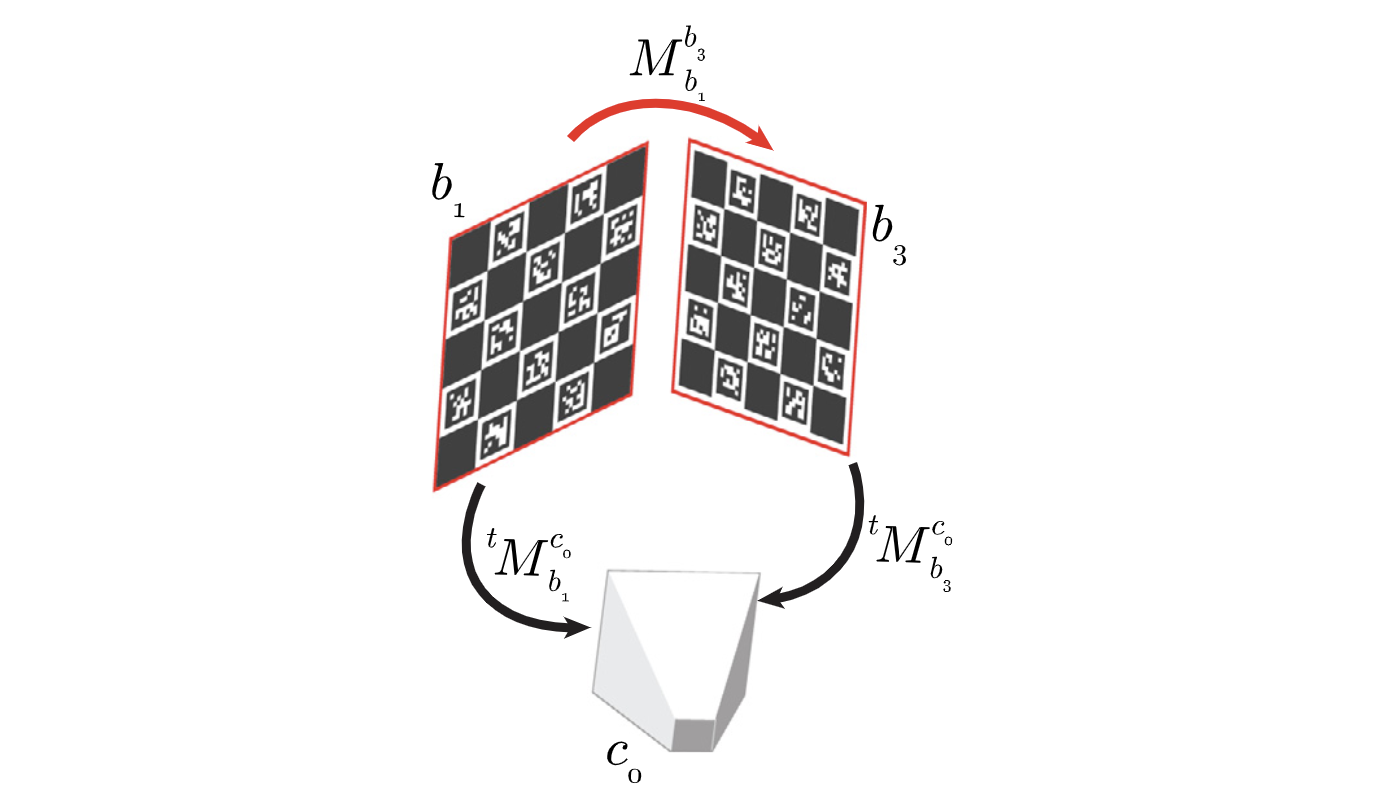
- 모든 frame을 거쳤을 때 board 간의 transformation 관계를 알 수 있으면 그룹화한다.
- 에서 각 카메라는 서로 다른 2개의 board를 관측하므로 (B1,B2)와 (B3,B4) 간의 transformation만 구할 수 있다.
- 에서는 camera1이 B2와 B3를 관측하므로 (B2,B3)의 transformation을 구할 수 있다.
- B1, B2, B3, B4 사이의 관계를 전부 알 수 있으므로 4개의 보드를 그룹화한다.
Grouping cameras as camera groups
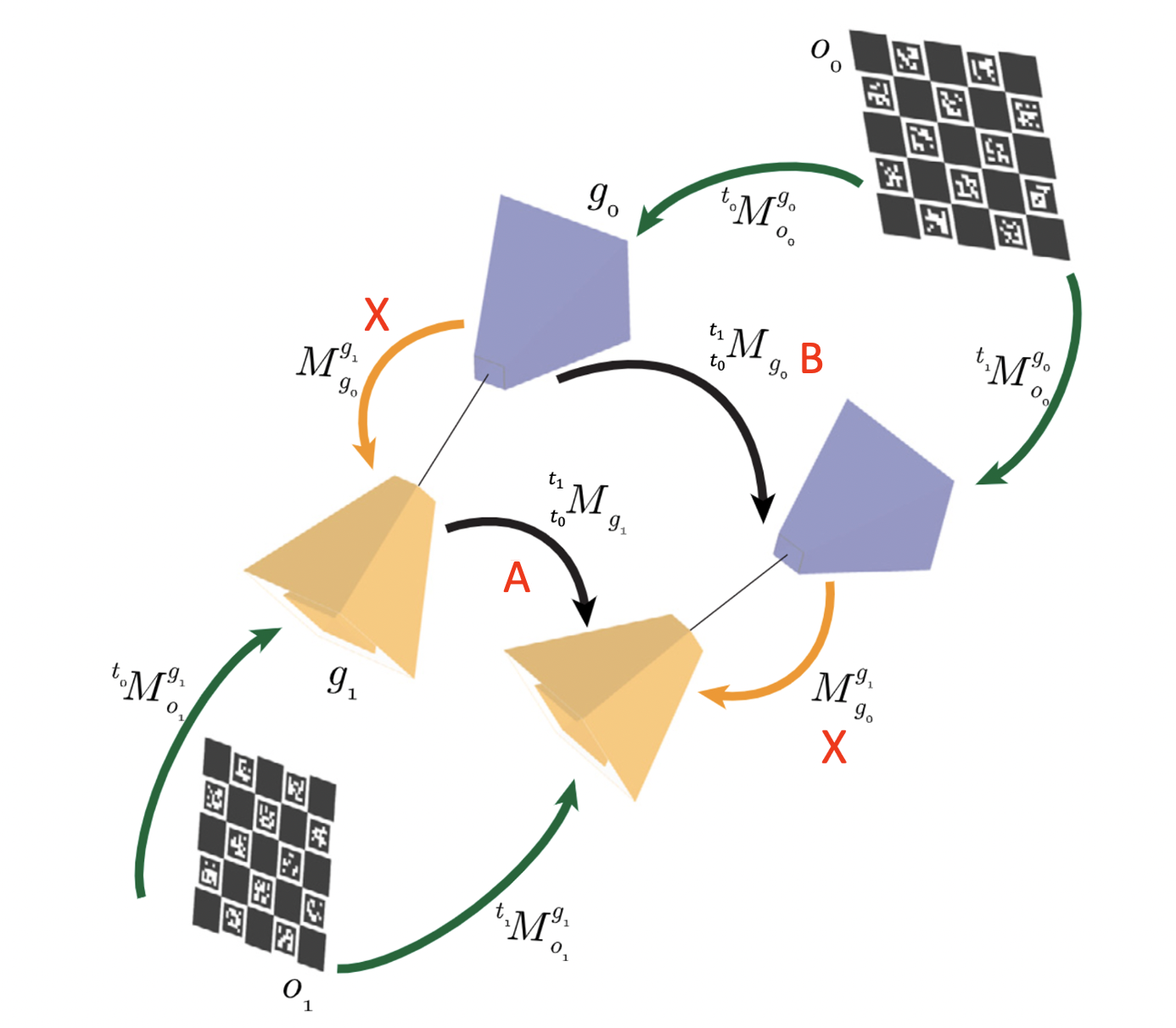
- 3D object를 만든 후 object로부터의 camera pose는 PnP 알고리즘을 통해 추정한다.
- 프레임에서 object 으로부터 camera 의 pose는 로 표현할 수 있다.
- 위 그림에서 3개의 카메라는 하나의 object를 동시에 보기 때문에 하나의 그룹 으로 묶어줄 수 있다.
- Inter-camera pose는 inter-board와 마찬가지로 여러 frame에서의 추정값을 평균 내어 사용하며 가장 작은 index를 가진 카메라가 reference가 된다.
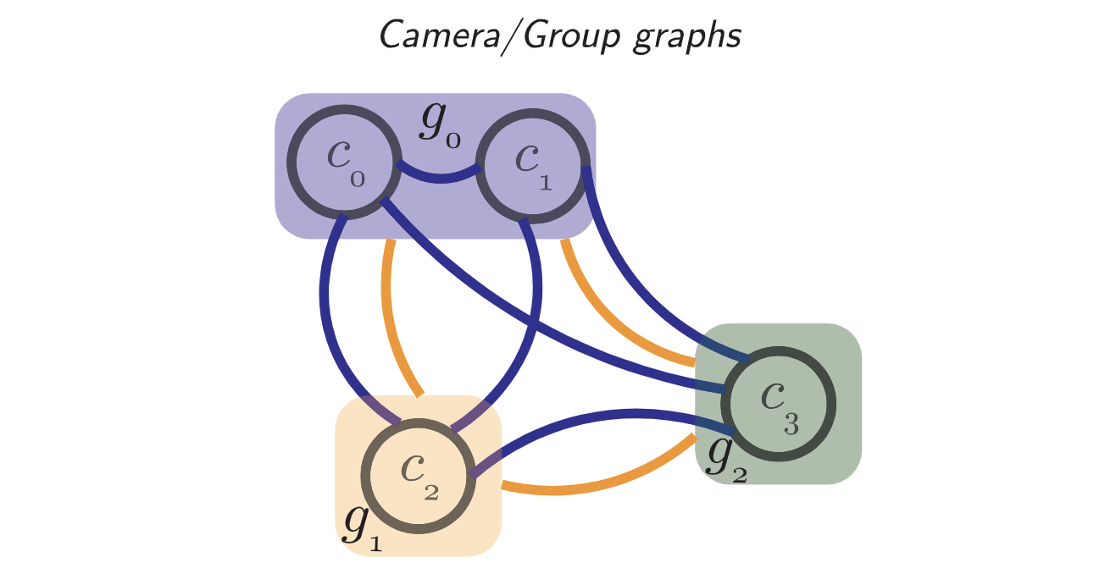
- Reference camera에 대한 camera들의 pose를 initialize할 때 다익스트라 알고리즘을 활용해 observation의 수를 최대화하는 경로를 찾는다.
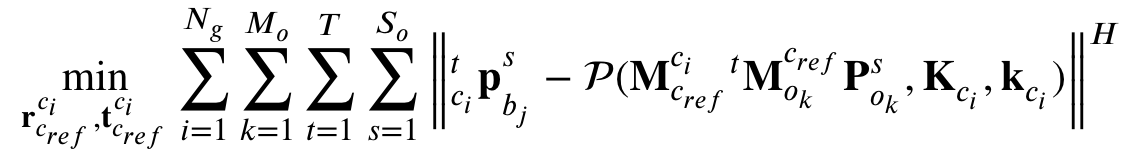
- 최종적으로 camera group은 위와 같은 cost function을 최소화하는 방향으로 refinement 한다.
Non-overlapping camera groups estimation
Hand-eye calibration for non-overlapping cameras
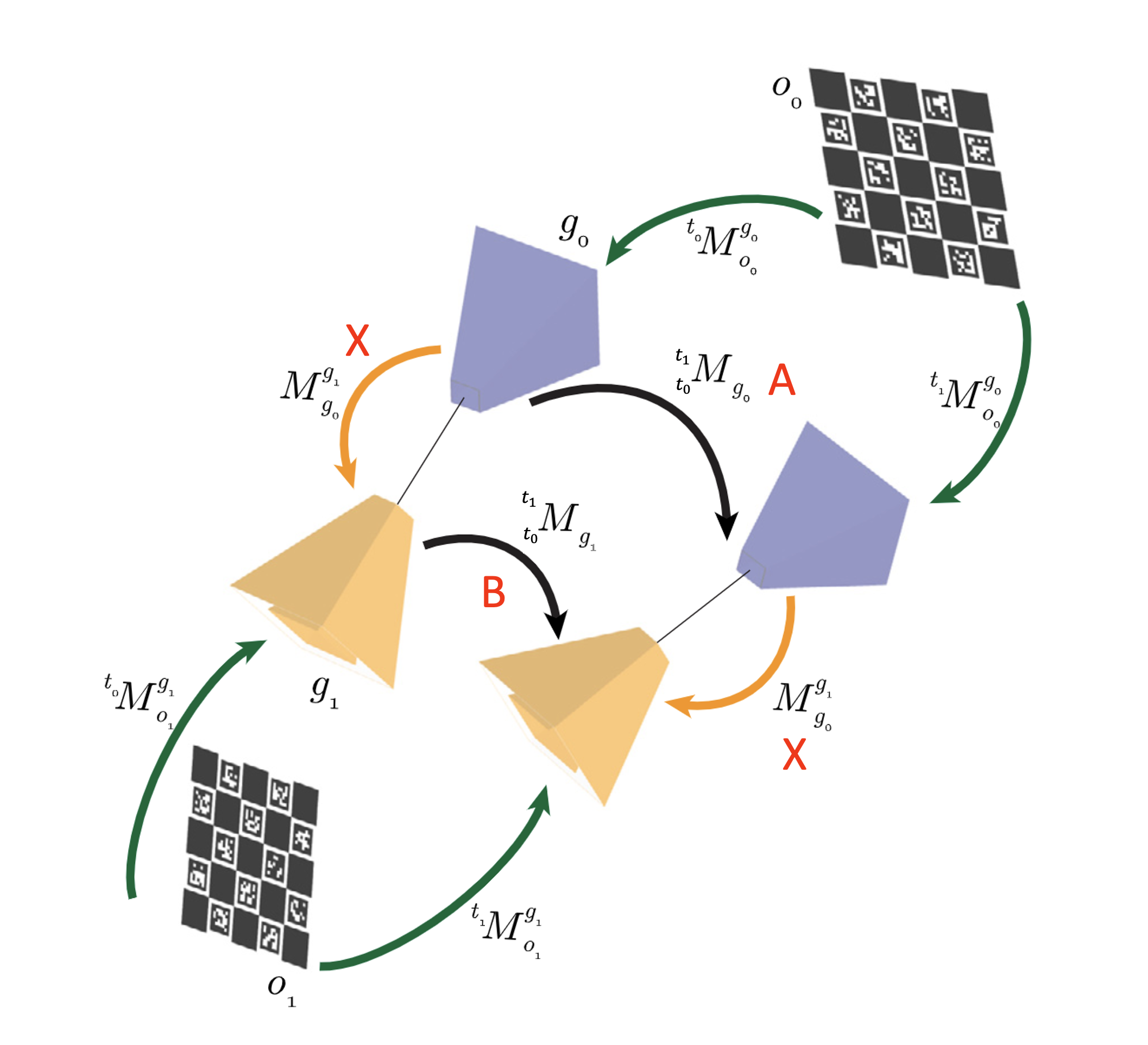
-
공통의 FoV가 없는 non-overlapping camera group이 남아있는 경우 hand-eye calibration을 활용한다.
-
프레임에 에서 으로 가는 변환과 프레임에 돌아오는 변환으로 루프를 만들어 를 구할 수 있다. -
프레임에 에서 으로 가는 변환과 프레임에 돌아오는 변환으로 루프를 만들어 를 구할 수 있다. -
모든 프레임에 대해 일반화할 수 있으며 의 형태가 된다.

-
Rotation equation으로부터 을 먼저 구한 뒤 translation equation을 통해 까지 구할 수 있다.
Best view selection and bootstrapped initialization
Best view selection
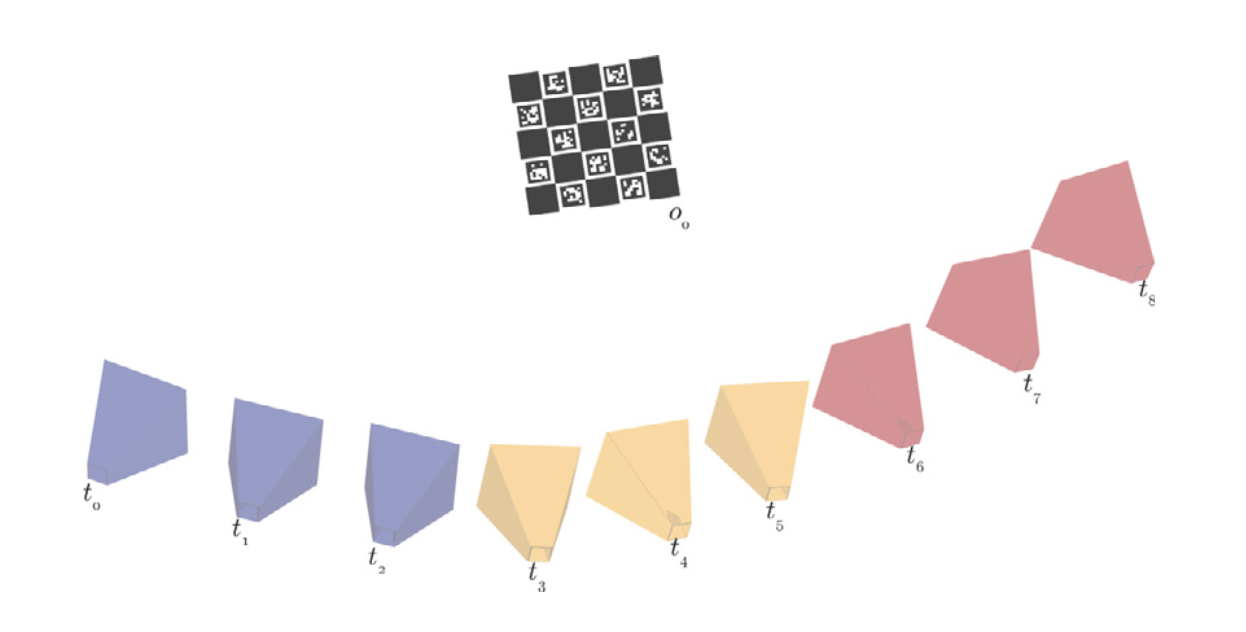
- Hand-eye calibration은 모든 프레임의 조합에 대해 적용할 수 있으나 영상이 길 경우 연산량에 문제가 있다.
- 또한, 연속된 프레임은 유사한 pose를 가지므로 큰 도움이 되지 않는다.
- Best view selection는 다양성을 극대화하고 outlier에 대해 robust하다.
- Translational component를 concat하여 유사한 pose들이 하나의 cluster로 구성되도록 만든다.
- K-means clustering을 활용하며 다양성을 보장하기 위해 rotation은 고려하지 않는다.
Bootstrapping
- 위 과정을 통해 20개의 initial clustering을 만든 뒤 배치마다 6개의 클러스터를 랜덤 샘플링한다.
- 6개의 pose로 hand-eye calibration을 수행하며 rotational error를 통해 검증하여 오차가 5도 미만인 경우만 저장한다.
- 배치는 200번 수행하며 rotation과 translation의 중앙값으로 최종 추정값을 정한다.
Merging camera groups and bundle adjustment
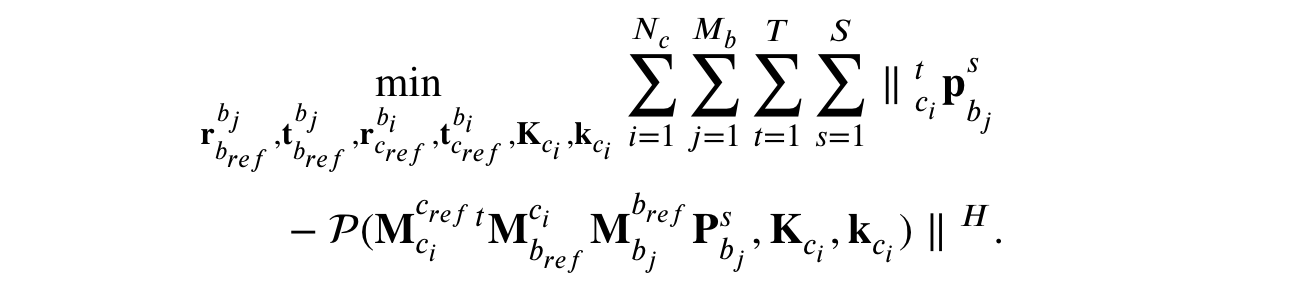
- Non-overlapping에 대한 initail pose 추정이 끝난 뒤 카메라 그룹과 objects는 그래프 알고리즘에 의해 합쳐진다.
- 최종적으로 모든 프레임에 대한 reprojection error를 통해 refinement 한다.
