Introduction
- 추천시스템에서 Matrix Factorization(MF)는 사용자와 아이템이 공유하는 잠재 벡터를 찾아 효과적으로 연관성을 찾는 모델이다.
- 그동안 MF의 성능을 향상시키기 위한 다양한 연구들이 진행되었지만 내적의 특성상 선형적인 관계를 표현하기에 그친다는 한계가 있었다.
- Deep nueral network는 그동안 CV, NLP 등의 분야에서 크게 발전하였으나 추천시스템에서는 단지 보조적인 정보를 모델링하기 위해서만 사용되었다.
- 본 논문에서는 내적 대신 neural architecture를 활용하여 더욱 복잡한 관계를 나타낼 수 있는 모델을 만든다.
Contributions
- DNN에 기반한 협력필터링 NCF를 제안한다.
- MF가 NCF의 특별한 케이스임을 보이며, 비선형적인 고차원 모델을 만들기 위해 다중 퍼셉트론을 이용한다.
- 다양한 실험을 통해 NCF의 효율성을 증명한다.
Preliminaries
Learning from implicit data
implicit 데이터에 대해 사용자와 아이템 간의 상호작용이 있을 때 1, 그렇지 않을 때 0으로 표현하는 매트릭스가 있다고 하자. 이 때 문제는 0이 부정적인 의견을 내포하는 것이 아니라 단순히 상관관계가 나타나지 않았음을 의미한다는 것이다. 결국, implicit 피드백에 대한 추천시스템의 문제는 관측되지 않은 관계에 대한 추정이 되며 이에 대한 loss function으로는 두 가지가 있다.
- point-wise loss: 회귀에 주로 쓰이는 방법으로 오차를 최소화한다.
- paoir-wise loss: 관측값이 관측되지 않은 값보다 큰 값을 가지도록 하여 두 값의 마진을 최대화한다.
NCF의 뉴럴네트워크를 활용한 모델을 위 두 가지 방식을 모두 충족시킬 수 있다.
Matrix Factorization
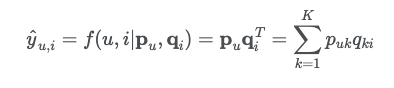
MF에서는 K차원의 latent space를 찾아 사용자의 잠재벡터인 와 아이템의 잠재벡터인 의 내적을 통해 를 추정한다.
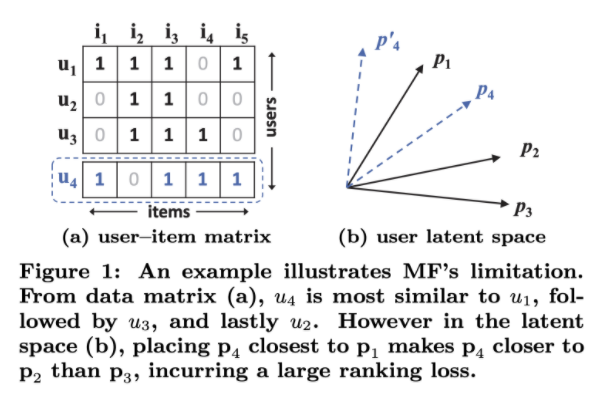
MF의 위 그림에서 볼 수 있다. u1, u2, u3의 유사도에 따라 벡터를 그리면 (b)와 같이 나오게 된다. 이 때, u4라는 새로운 데이터에 대해 유사도를 측정하면 u1>u3>u2의 순으로 u4와 유사하지만 (b)의 그림에서 이를 표현할 수 있는 벡터를 그리는 것이 불가능함을 알 수 있다. 즉, 저차원 공간에서의 한계점이 나타나며 DNN의 비선형성을 통한 해결점이 있음을 알 수 있다.
Neural Collaborative Filtering
General Framework
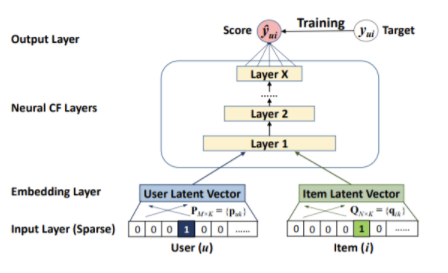
- input으로 사용자와 아이템의 one-hot encoding 벡터를 사용한다.
- embedding layer에서 dense vector로 변환된다. 이 임베딩 과정이 MF 모델에서의 잠재벡터와 같은 역할을 한다고 볼 수 있다.
- Neural collaborative filtering layers에서는 score를 예측하는 역할을 수행한다.
- 예측한 score와 실제값의 binary cross entropy를 줄이는 방식으로 학습한다.
Generalized Matrix Factorization(GMF)
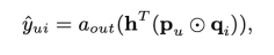
단순히 dot-product로 output을 예측했던 MF와 달리 GMF에서는 element-wise product를 수행하며, 가중치를 적용해준후 활성화함수를 통과한다. 활성화함수로는 시그모이드를 사용하였다.
Multi-Layer Perceptron(MLP)
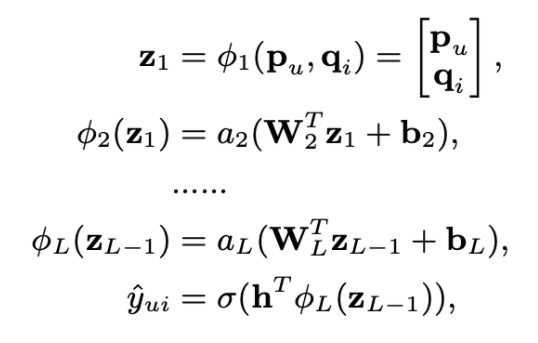
Element-wise product를 수행하여 뉴럴 네트워크로 넘겨주었던 GMF와 달리 MLP에서는 Concatenate한 후 뉴럴 네트워크의 input으로 들어간다.
Fusion of GMF and MLP
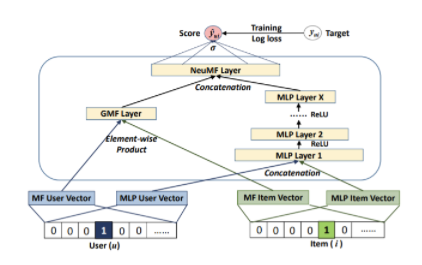
앞서 보았던 GMF와 MLP를 함께 활용한 모델 구조이다. 각각의 네트워크를 수행한 후 concatenation을 통해 합친다. 합칠 때 가중치를 통해 영향력을 조정할 수 있으나 0.5를 사용하였고 최종적으로 시그모이드를 거쳐 예측 output을 도출한다.
선형적인 특성을 가진 GMF와 비선형적인 특성을 가진 MLP가 합쳐져 사용자와 아이템 간의 복잡한 관계를 표현할 수 있다는 장점이 있으며, 두 모델을 각각 최적화 함으로써 서로 다른 사이즈의 임베딩을 가진다는 것도 특징이다.
Experiment
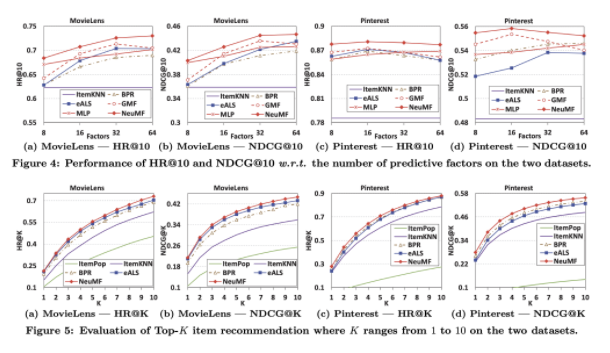
- HR@10과 NDCH@10에 대한 각 모델 별 성능 평가표를 비교해본 결과 NeuMF가 모든 경우에서 SOTA를 달성하는 모습을 보였다.
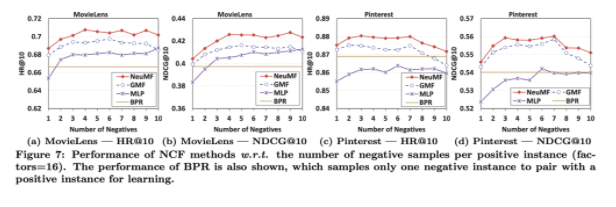
- point-wise loss의 경우 negative sampling ratio를 조절할 수 있다. 실험 결과 3~6 사이에서 최적이었다.
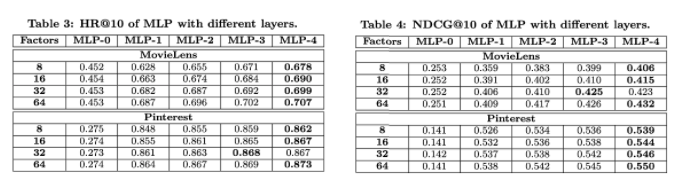
- MLP에서 레이어를 늘릴수록 더 성능이 좋은 것으로 보아 DNN이 효과적임을 알 수 있다.
