[3강] Optimization

최적화

우리는 이전 강의에서 손실 함수(loss function) 이라는 개념을 배웠고 이를 최소화하는 W (weight matrix) 를 구하고자 한다. 이를 위해서 여러 전략을 생각해볼 수 있다.

• Random Search
  임의 가중치를 시도하고 가장 잘 작동하는 것을 선택하는 방식
• Random Local Search
  $W$에 무작위 값을 더한 새로운 $W_n$에 대해 loss가 더 낮다면 이를 택하는 방식
• Gradient
  손실 함수에 대한 기울기 (미분) 값을 계산하는 방식.
  이 방식이 가장 효율적이다.

모든 차원에 대한 손실 함수의 편도함수를 계산하여 numerical gradient를 구하는 방법이 있다.
이 방법은 파라미터의 갯수가 늘어날수록 더 느려지므로 현실적으로 사용하기 힘들다.
대신에 Calculus를 사용하여 analytic gradient를 계산해볼 수 있다.

Gradient Descent

while True:
  weights_grad = evaluate_gradient(loss_fun, data, weights)
  weights += - step_size * weights_grad # perform parameter update

손실함수의 기울기를 반복적으로 평가하여 매개 변수 업데이트를 수행하는 과정을 Gradient Descent 라고 한다.

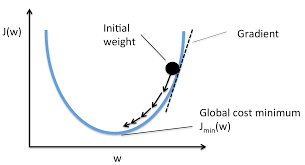
실제로는 매우 고차원의 함수일 경우가 다분하지만, 이해를 쉽게 하기 위해서 2차원으로 생각해보자. 위 그림에서 x축을 $W$, y축을 손실 함수라고 정의하겠다. initial weight은 맨 처음 W값이다.
이 W를 손실 함수의 기울기가 점점 작아지는 방향을 따라 이동시키면, loss를 가장 작아지게 하는 W를 구할 수 있을 것이다.
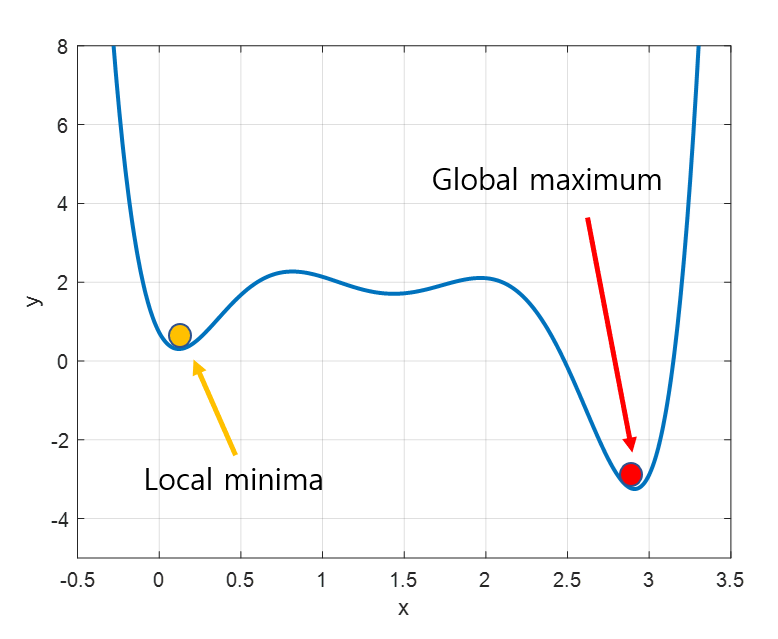
만일 해당 지점이 손실 함수의 극소점이면 local optima, 최대점이면 global optima라고 한다.

Mini-batch Gradient Descent

데이터 셋이 수백만 개라면, 이들 데이터 모두에 대해 gradient를 계산하는 것은 매우 비효율적이다. 데이터 셋 중 일부 샘플만 뽑아서 gradient를 계산하는 방식을 mini-batch gradient descent라 하며, 근사치를 이용하기 때문에 100%에 가까운 정확성은 아니지만, 빠르게 작업할 수 있다.

Stochastic Gradient Descent (SGD)

이 방법은 batch size = 1로 지정하여 gradient를 계산하는 극단적인 방식이지만, 실제로는 SGD와 MGD와 같은 의미로 쓰는 경우가 많다.

batch size

배치 크기는 일종의 하이퍼 파라미터이므로 프로그래머가 직접 지정해주어야 한다. 보통은 메모리 크기가 클수록 큰 값을 사용하고, 8, 16, 32 등 2의 배수로 값을 지정한다.

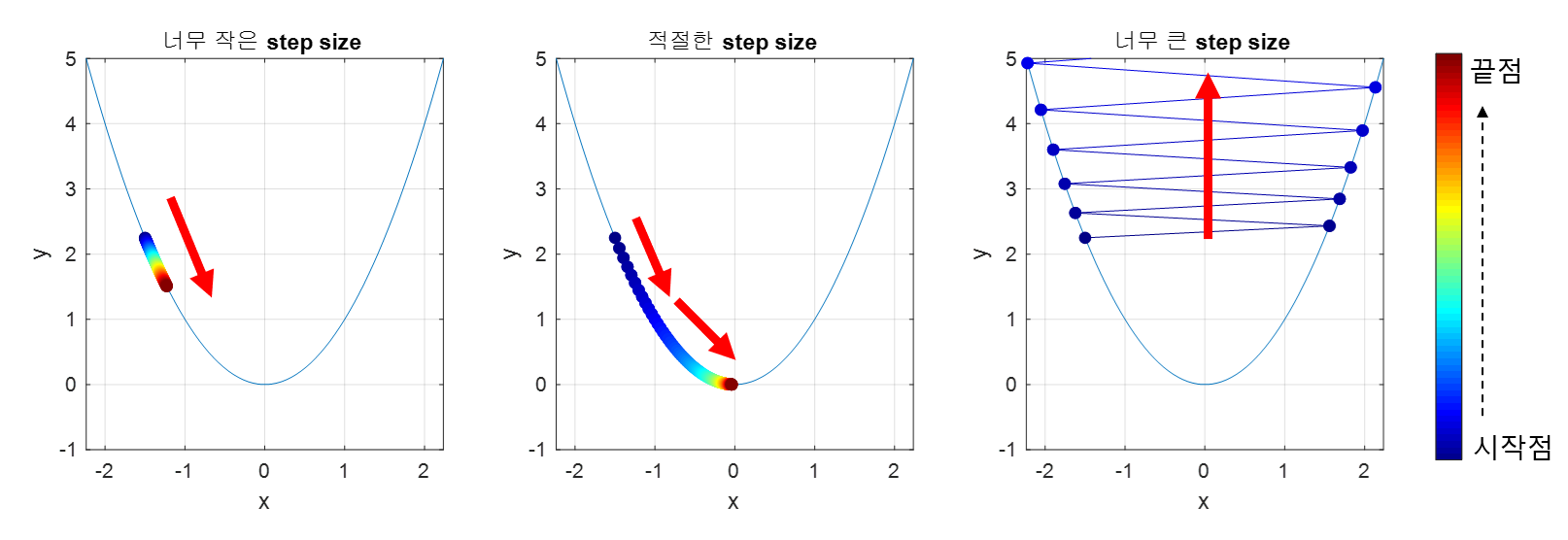
step size

gradient descent를 이용하면 loss function의 기울기가 가장 가파른 방향을 알려주지만, W가 얼마나 이동해야 하는 지를 알려주지는 않는다. 이러한 이동량에 대한 하이퍼 파라미터를 learning rate 라고 한다. 이 값이 너무 작으면 꾸준히 loss가 낮아지긴 하겠지만 보폭이 작아서 학습 속도가 매우 느려진다. 반면에 이 값이 너무 크면 loss로 수렴하지 않고 오히려 발산해버리는 경우가 생길 수 있어서 적당한 값을 찾는 것이 매우 중요하다.
일반적으로는 0.01, 0.001, 0.0001 등의 값을 취한다.