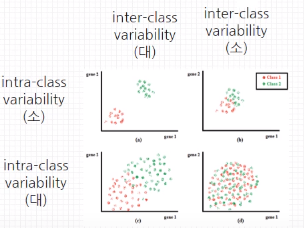
데이터의 분포에 대한 개념이다.
- Intra Class Variability : 클래스 내부 다양성 → 낮을수록 좋다
- Inter Class Variability : 클래스 간 다양성 → 높을수록 좋다
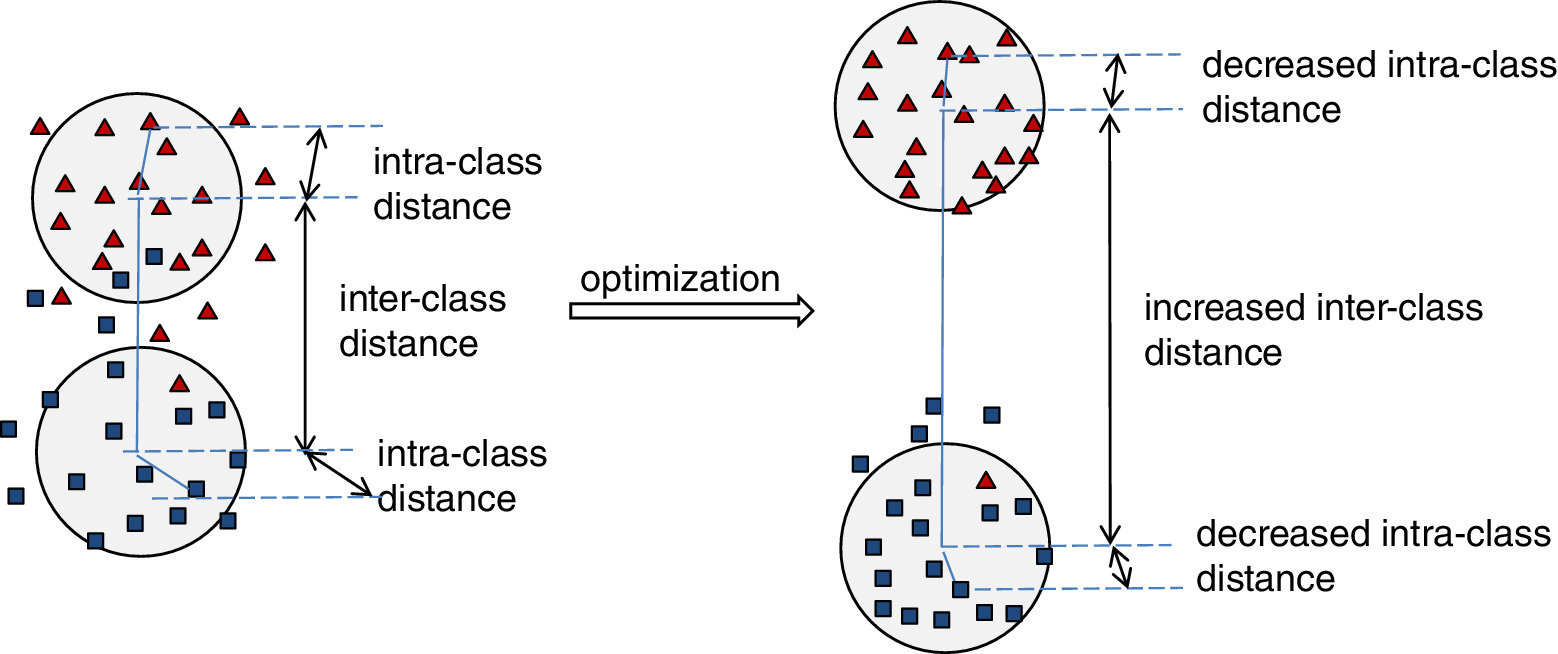
Variability가 아니라 Distance라고 생각해도 좋다
Intra Class Variability
A라는 분류를 갖는 데이터들의 특성이 서로 유사할수록 모델은 이들을 A라고 인지하기 쉬워진다. 반면에 특성이 다양할수록 이들이 가지는 공통적인 특성을 모델이 학습하기는 더 어려워진다. 예를들면 강아지 중에서도 푸들에 한정해서만 분류해도 된다면 난이도가 쉬워지지만, 강아지라는 종 전체에 대해서 판별해야 한다면 보다 어려울 것이다. 이 경우가 Intra Class Variability가 높은 경우이다. 그러므로 어떠한 분류에 대한 데이터 분포를 좁게 구성할수록 학습이 쉬워진다고 볼 수 있다.
Inter Class Variability
여기에 B라는 분류를 갖는 데이터들이 추가되었다고 하자. 이러한 데이터 셋이 A와 유사도가 높지만, 다르게 분류되어야 한다면 위 그림에서 왼쪽처럼 분류가 더 어려워질 것이다. 예를들면 성견과 아기 강아지 간에 분류해야 한다면? 아니면 거봉과 켐벨이라던가.. 이런 경우에는 데이터셋끼리 유사점이 많아서 난이도가 높다. 이 경우가 Inter Class Variability가 낮은 경우이다. 더군다나 Intra Class Variability 까지 높다면 실제 결과에서 오검출이 발생할 확률이 높아질 것이다. 그러므로 어떠한 분류를 갖는 데이터 셋 간의 거리를 크게 유지할수록 더 좋은 성능을 기대할 수 있다.
데이터 셋의 중요성
이 경우에는 단순히 학습량을 늘리거나 하이퍼 파라미터를 튜닝하거나, 심지어 모델의 구조를 바꾸더라도 성능을 더 이상 향상 시키지 못할 수도 있다. 극단적으로는 벤치마크 성능이 우월한 모델 구조를 가져도 일정 수준이상 loss가 줄어들지 않을 수도 있다. 그러므로 머신러닝이나 딥러닝은 모델의 성능이 아무리 좋아도 데이터 셋의 의존도가 매우 높을 수 밖에 없기에 데이터 셋에 대한 검수, 편향되지 않는 데이터 구성, 분류 기준의 명확화 등이 굉장히 중요하다.