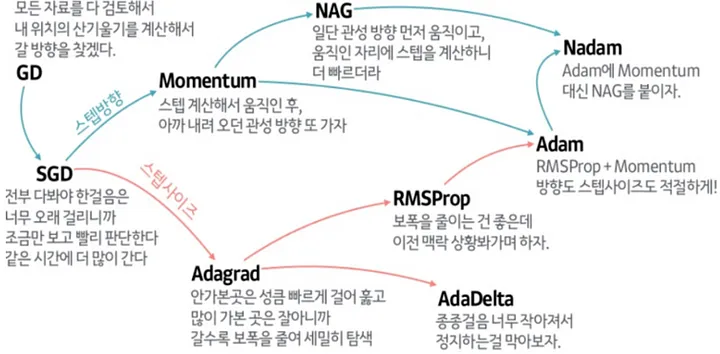

Gradient Descent (GD) 과정을 효율적으로 수행하게 해주는 것이 Optimizer이다.
다만 GD는 모든 데이터 셋을 전부 이용해서 기울기를 계산하므로 현실적이지 않아서 여러 해결책이 등장하게 되었다.
위 그림처럼 local minima에 빠져버리는 문제도 있지만, 전체 데이터를 다 사용하는건 일단 메모리도 부족하다.
SGD (Stochastic Gradient Descent)
전체가 아닌 일부 미니배치만 추려서 GD를 수행한다. 이 경우에도 GD에서의 문제점이 잔재해 있다.
Momentum
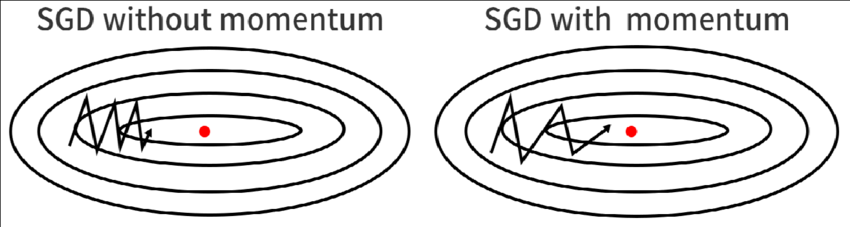
이동 방향으로의 관성을 주어 해당 방향으로 보다 빠르게 수렴하도록 한다.
NAG (Nesterov Accelerated Gradient)
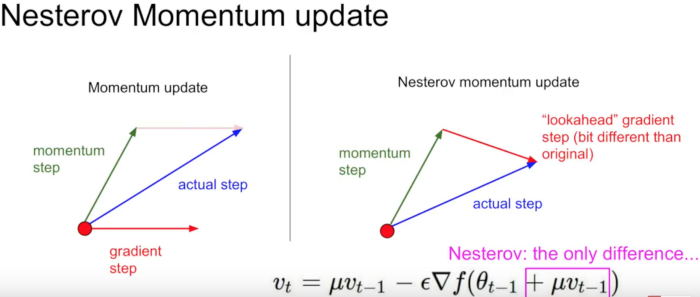
모멘텀만큼 어느정도 이동하고 그 자리에서 다시 계산한다
Adagrad
자주 등장하거나 변화를 많이 한 변수들의 경우 optimum에 가까이 있을 확률이 높기 때문에 작은 크기로 이동하면서 세밀한 값을 조정하고, 적게 변화한 변수들은 optimum 값에 도달하기 위해서는 많이 이동해야할 확률이 높기 때문에 먼저 빠르게 loss 값을 줄이는 방향으로 이동하려는 방식이라고 생각할 수 있겠다.
현실에서의 탐색 방식과 유사하다. 없을 것 같은 곳은 대충 훑고, 있을 것 같은 곳을 세밀하게 탐색하는 느낌의 방식이다.
RMSProp
Adagrad에서 사용되는 G_t라는 값이 무한히 커지는 단점을 극복하기 위해 지수 이동평균을 적용한 방식이다.
가장 최근의 기울기에 대한 가중치를 높게 반영한다고 한다
Adam
RMSProp과 Momentum 기법을 합친 방식.
잘 모르면 결국 Adam이다. 경험적으로 봤을때 대부분 잘 동작한다.
다만 때에 따라선 다른 optimizer(RMSProp, Adagrad)가 조금이나마 더 잘 동작하는 경우도 있어서 여러 방식을 시도해보는 것도 좋다.