확률(2)

김민주·2025년 4월 8일

GK

목록 보기

8/15

확률 이론의 기본 개념

1. 확률 공간 (Probability Space)

1.1 표본공간 (Sample Space, Ω)

정의: 가능한 모든 결과의 집합. 예를 들어, 동전 던지기의 표본공간은
Ω={H,T} 입니다.

특징: 실험이나 관측에서 나올 수 있는 모든 가능성을 포괄.

1.2 사건 (Event)

정의: 표본공간의 부분집합으로, 관측 가능한 특정 결과나 그들의 모임.

예: 주사위를 던졌을 때 짝수가 나오는 사건

A={2,4,6}.

1.3 확률 측도 (Probability Measure)

정의: 각 사건에 대해 0과 1 사이의 값을 할당하는 함수

확률 공간에서 사건의 확률을 수학적으로 정의하는 함수
특정 집합의 크기를 재는 방식으로 확률을 할당
P:F→[0,1].

공리 (콜모고로프 공리):
공리(Axiom)는 수학에서 증명 없이 받아들이는 기본적인 원칙이나 규칙

<확률 측도의 공리>

전체 확률: P(Ω)=1 (전체 표본공간의 확률은 1)
비음성성 : P(A)≥0 (모든 사건의 확률은 음수가 아님)
가산 가법성: 상호 배타적인 사건들의 합집합에 대한 확률은 각 사건의 확률의 합과 같다.

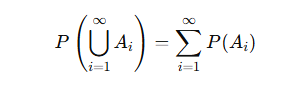
2.조건부 확률과 독립성

2-1. 조건부 확률

정의: 사건 B가 일어난 상황 하에서 사건
A가 일어날 확률을 P(A∣B)로 표기

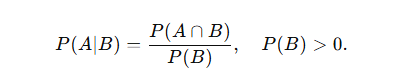
2-2. 독립 사건(Independence)

두 사건 A, B가 서로 영향을 미치지 않은 것

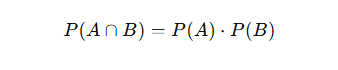
조건부 독립성 : 사건 B의 발생 여부와 관계 없이 A의 발생확률이 동일하면 독립이라고 봄

3. 무작위 변수(Random Variables)와 분포

3-1. 무작위 변수의 정의

표본 공간의 각 원소에 실수 값을 할당하는 함수

X:Ω→R

3-2. 확률 질량 함수- 이산형변수 (Probability Mass Function, PMF) – 이산형 변수

정의: 이산형 무작위 변수 X의 경우, 각 이산적인 값 x에 대해 그 값이 나타날 확률을P(X=x)로 나타냅니다. 이를 함수 형태로 표현한 것이 확률 질량 함수(PMF)

특징

합이 1 : 이산형 변수 X가 가질 수 있는 모든 가능한 값 x에 대해 P(X=x)=1.
비음수 : P(X=x)≥0

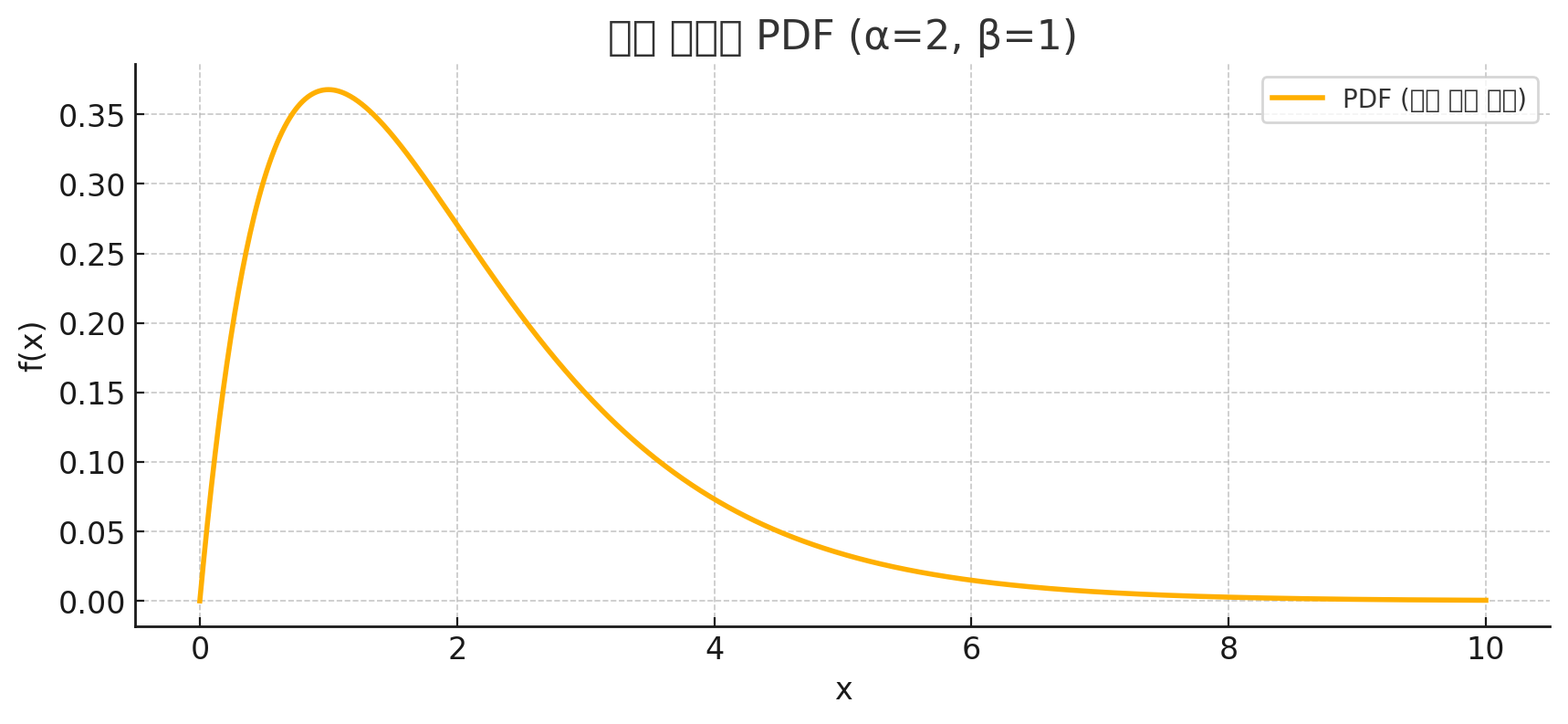
3-3. 확률 밀도 함수(Probability Density Function, PDF) - 연속형 변수

정의:
연속형 무작위 변수 X는 특정 값에서 직접 확률을 가지지 않으며, 대신 확률 밀도 함수 f(x)를 통해 확률의 '분포'를 기술합니다.

특징
비음수 조건: f(x)≥0 모든 x에 대해 성립
전체 확률의 적분 :
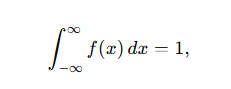
즉, 연속 전체 구간에 대해 확률의 총합(적분값)은 1

PDF VS 신뢰구간 비교

PDF : 데이터 자체의 분포를 그린 그림
신뢰구간 : 모수가 어디쯤 있는지 추정
EX. 평균 μ는 **대략 95% 확률로 [3.1, 3.9] 안에 있을 거야”
→ 이건 모수에 대한 불확실성을 설명하는 구간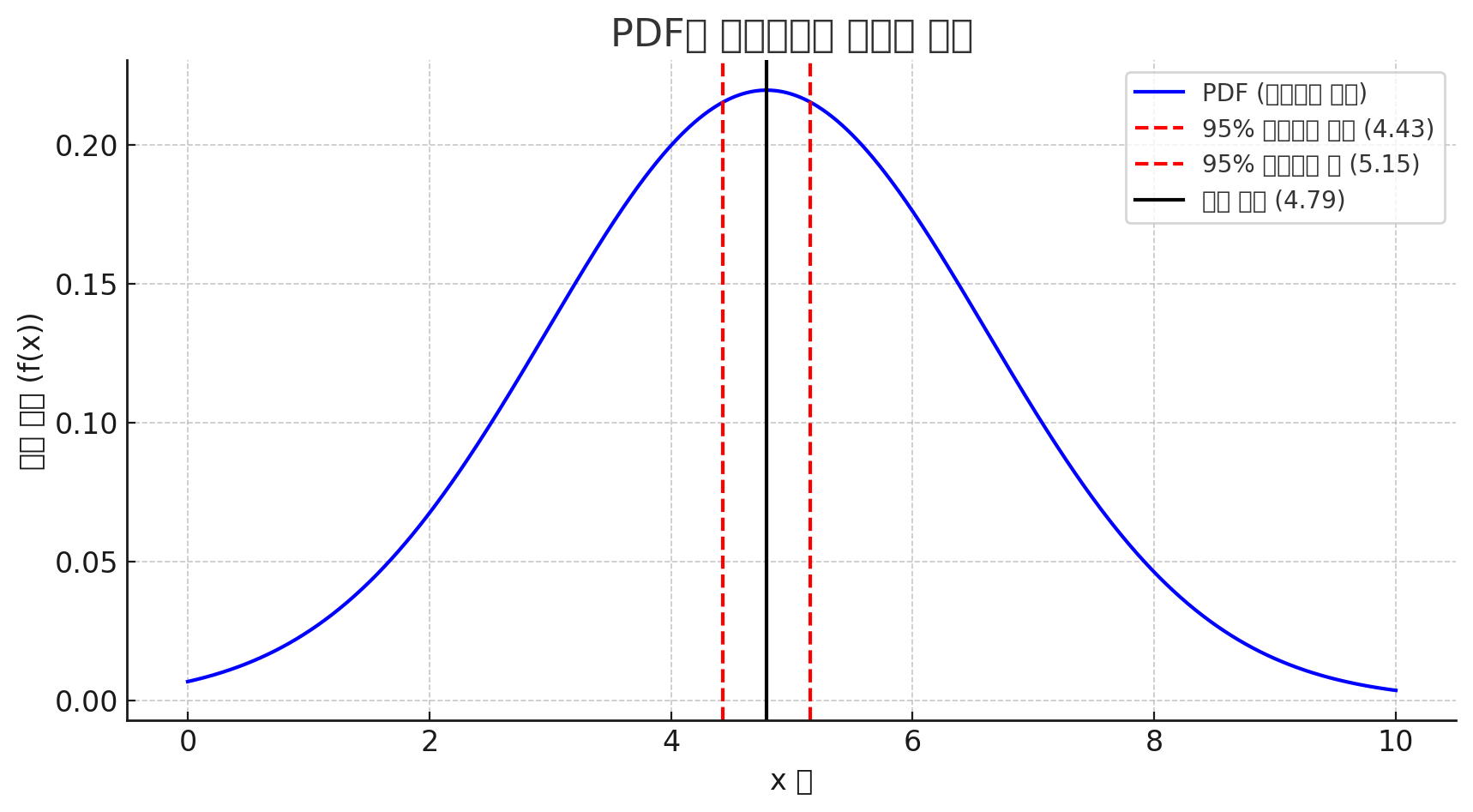
파란 곡선 : PDF(확률 밀도 함수)
검은 선 : 표본 평균
빨간 점선 : 95%의 신뢰구간
우리가 뽑은 데이터로 추정한 결과, 모평균은 이 범위안에 있을 확률이 95%다 라는 의미

3-4. 누적 분포 함수(Cumulative Distribution Function, CDF)

정의 :
누적 분포 함수 F(x)는 무작위 변수 X가 x 이하의 값을 가질 누적 확률
x값이 커질수록 지금까지 누적된 확률이 점점 더 쌓여감

y축 F(x)는 → P(X ≤ x)

"x까지 사건이 일어날 누적 확률"을 보여주는 그래프

출처 : https://datacookbook.kr/54

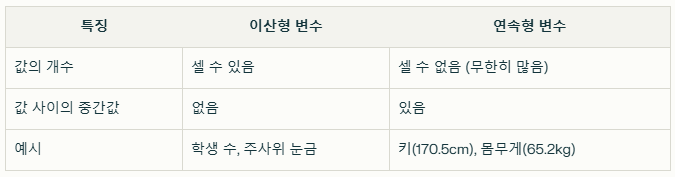
<이산형 변수 VS 연속형 변수>

4. 기댓값, 분산, 모멘트

확률 변수의 특성을 수치화 하는데 사용되는 도구

4-1. 기댓값

정의 : X가 취할 수 있는 값들을 가중 평균한 값으로 "중심"위치를 나타냄
중심 위치: 기대값은 데이터나 확률 분포의 중심 위치를 나타내며, 평균적인 경향성을 이해하는 데 중요한 역할을 합니다.
예측: 미래의 결과를 예측할 때, 기대값은 "평균적으로" 어떠한 결과가 나타날지를 제시합니다.
선형성: 기대값은 선형 연산자이므로, 두 확률 변수의 합에 대한 기대값은 각각의 기대값의 합과 같다는 성질(즉, E[aX+bY]=aE[X]+bE[Y])을 가집니다

4-2. 분산(Variance)

정의 : 분산은 무작위 변수 X의 값들이 평균 E[X]에서 벗어난 정도를 제곱한 후, 그 제곱된 값들의 평균을 구하는 방식으로 정의
데이터의 산포도를 나타냄
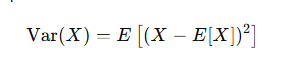
제곱을 하는 이유 ?
편차가 음수와 양수로 상쇄되지 않도록 하기 위해
단위의 제곱: 분산은 원래 단위의 제곱(예: 길이가 미터라면 분산은 제곱미터)으로 나타납니다. 이 때문에 해석 시 주의해야 하며, 필요에 따라 표준편차(분산의 제곱근)를 사용하는 경우가 많습니다.

특징

산포 정도 측정: 분산 값이 작으면 X의 값들이 기대값 주위에 몰려 있음을 의미하고, 값이 크면 퍼짐 정도가 크다는 것을 나타냅니다.

모멘트 관계:
X제곱은 2차 모멘트라고 하며, 기대값과 함께 분산을 통해 분포의 산포 특성을 파악할 수 있습니다.

4-3. 고차 모멘트와 모멘트 생성 함수 (MGF)

확률 분포의 '모양'을 더 자세히 설명해주기 위해 사용되는 척도

모멘트?

무작위 변수 X에 대해 (N차 모멘트)를 구하는 것을 의미.

n은 양의 정수
n=1이면 1차 모멘트로 기댓값(평균)을 나타냅니다.
n=2이면 2차 모멘트가 나오고, 이 값은 분산을 계산하는 데 사용되거나 분산 자체와 연관됩니다.
고차 모멘트는 n≥3인 경우를 말하며, 이는 단순히 평균과 산포도를 넘어서 분포의 모양에 관한 정보를 제공합니다.

왜 ‘중앙화된’ 모멘트를 사용하는가?
중앙화된 모멘트:
E[(X−E[X]) N제곱] 같이 평균을 빼고 제곱 또는 세제곱, 네제곱 등의 연산을 하는 이유는 각 값들이 평균에서 얼마나 떨어져 있는지를 정확하게 파악하기 위함입니다.

중앙값으로부터의 차이를 사용하면 값들이 평균보다 크거나 작은지에 관계없이, 분포가 얼마나 퍼져 있는지 또는 어느 쪽으로 치우쳤는지를 균형 있게 반영할 수 있습니다.
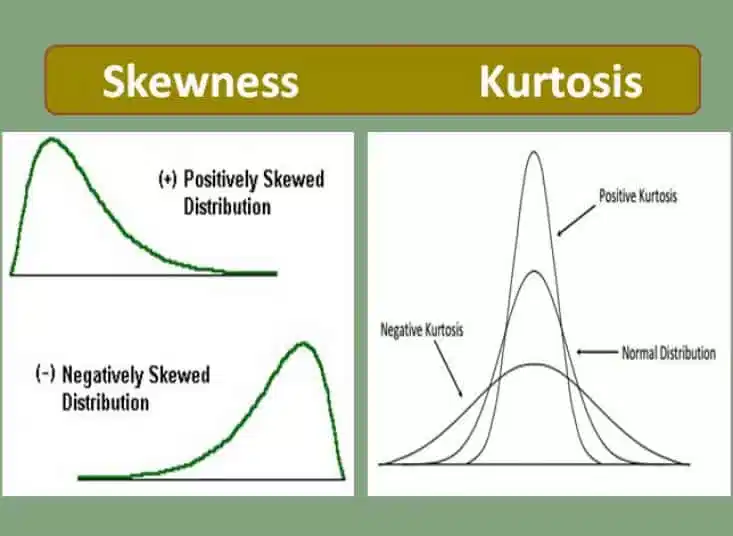- 왼쪽 사진(왜도), 오른쪽 사진(첨도)

출처 : https://www.excelr.com/skewness-and-kurtosis

5. 확률 분포의 주요 예시

5-1. 이산 확률 분포

1. 베르누이 분포 (Bernoulli Distribution)

정의:
베르누이 분포는 단 하나의 시행(trial)에서 두 가지 결과(성공과 실패) 중 하나가 발생하는 경우를 나타냅니다.
예를 들어, 동전을 던져서 앞면(H)이 나오면 성공, 뒷면(T)이 나오면 실패로 보는 경우

2. 이항 분포 (Binomial Distribution)

- 정의 : 독립적인 베르누이 시행을 N번 반복할 때, 그 중 성공이 몇 번 발생하는지 모델링함

3. 포아송 분포(Poisson Distribution)

정의 : 단위 시간이나 단위 공간 내에서 발생하는 어떤 사건의 개수를 모델링하는데 사용됨
사건이 드물게 발생하는 상황에 적합

특징:

사건들이 독립적으로 발생하며, 동일한 단위 구간에서 발생하는 사건의 수가 평균 λ 주변에서 분포합니다.
기댓값과 분산 모두 λ로 동일합니다.

예시: 1분 동안 웹사이트에 접속하는 사용자 수, 1시간 동안 특정 교차로에서 발생하는 교통사고 수 등.

4. 기하 분포(Geometric Distribution)

정의 : 베르누이 시행에서 첫 번째 성공까지 걸리는 시행 횟수를 모델링하는 분포
=> "성공"이 처음으로 나타날 때까지 몇 번의 시행이 필요한지를 나타냄

5-2. 연속 확률 분포

1. 정규 분포(Normal Distribution)

정의 : 평균을 중심으로 좌우 대칭인 종 모양의 분포

특징
대칭성을 가지므로 평균, 중앙값, 최빈값이 모두 같음
68-95-99.7 법칙: 약 68%의 데이터가 μ±σ, 95%가 μ±2σ, 99.7%가 μ±3σ 안에 위치합니다

2. 지수 분포(Exponential Distribution)

정의 : 사건 발생 간의 시간 간격을 모델링하는데 자주 사용

ex) 특정 이벤트(전화 도착, 기계 의 고장 등)가 다음에 언제 발생할지 예측할 때 사용됨

특징 : 메모리리스 성질 - 과거에 사건이 발생한 시간이 미래에 발생할 시간에 영향을 주지 x

출처 : https://woochan-autobiography.tistory.com/112

3. 감마 분포(Gamma Distribution)

정의 : 지수 분포를 일반화 한것
지수 분포를 일반화한 것, 단위 시간 내에 여러 사건이 발생하는 시간 간격의 합이나, 대기 시간의 총합 등을 모델링할 때 사용

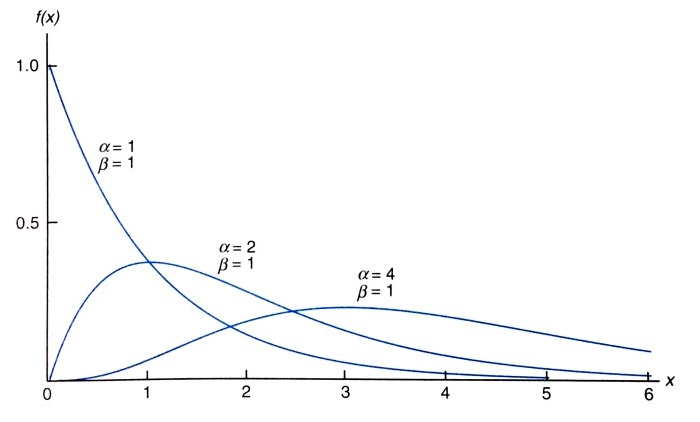
출처 : https://for-my-wealthy-life.tistory.com/56

4. 베타 분포

정의 : 확률 또는 비율과 같은 0과 1 사이의 값들을 모델링하는데 사용
어떤 사건의 성공률이나 확률
에 대한 사전 분포로 활용됨

특징

다양한 형태를 띠므로, U자형, 종 모양, 편향된 분포 등 여러 모양을 가짐
베이지안 통계학에서 중요한 역할을 하며, 사전 분포나 사후 분포로 자주 사용됨

6. 확률의 극한 정리들

6-1 법칙의 수렴 (Law of Large Numbers)

많은 표본을 모으면, 그 표본들의 평균이 모수(즉, 분포의 실제 평균)에 가까워진다
약한 법칙 : 독립이고 동일한 분포를 따르는 무작위 변수들의 평균이 진짜 평균에 수렴한다는 원리.
=> 표본 크기가 충분히 커지면, 표본 평균이 모평균과 크게 벗어날 확률이 0에 수렴합니다. 이 결과는 다양한 통계적 추정 방법(예: 추정치의 일관성)에 기초

강한 법칙: "거의 모든" 실현 경로(표본의 결과)에서, 무한히 많은 표본을 관찰하면 표본 평균은 정확히 모평균에 수렴한다는 강한 보장을 제공합니다. 이는 개별 실험의 결과에 의존하지 않고, 이론적으로 거의 모든 경우에서 성공적인 수렴을 보장

6-2 중심 극한 정리 (Central Limit Theorem, CLT)

정의: 개별 분포의 형태와 상관 없이, 충분히 많은 독립 확률 변수들의 합(또는 평균)을 정규화(normalization)하면 근사적으로 정규 분포를 이룬다

실제 응용:

통계적 추정: 표본평균을 이용한 모평균 추정의 정규성을 가정하여 신뢰구간을 설정할 수 있음.

가설 검정: 표본의 통계량이 정규분포에 근사하기 때문에 z-검정, t-검정 등 정규성에 기반한 검정방법을 사용할 수 있음.

산업 및 품질 관리: 대량의 데이터를 취급하는 경우, 평균값의 분포가 정규에 가까워지므로, 품질 관리나 공정 통계에서 유용하게 활용

주요 조건: 독립성, 동일 분포(혹은 약한 종속 조건) 등이 필요하며, 표본 크기가 클수록 근사가 더 정확해짐.

=> 법칙의 수렴과 중심 극한 정리 모두 표본 크기의 증가가 추론에서 가지는 중요성을 강조

7. 확률 계산의 추가 도구

7-1. 조건부 기댓값 (Conditional Expectation)

정의 :

조건부 기댓값 E[X∣Y]는 어떤 확률 변수
X의 기댓값을, 다른 변수 Y의 특정 값이나 정보를 알고 있을 때 계산한 값입니다.
이는 “주어진 조건 하에서의 평균”이라고 생각할 수 있습니다.

예를 들어, 주사위를 던졌을 때 앞면이 특정 조건(예: 짝수)이 주어졌다면, 그 조건 하에서 얻을 수 있는 기대값을 산출하는 것이 조건부 기댓값

예측 및 베이즈 추정 시 사용
변수 간 관계 반영 - x와 Y 사이의 의존 관계를 반영하므로, 단순 전체 평균만 계산하는 것보다 더 세말한 정보 제공
확률 과정 및 시계열 분석

7-2. 치비셰프 부등식