Regression Performance Metrics

• 회귀 모델의 성능을 평가하는 데 일반적으로 사용되는 네 가지 지표는 평균 제곱 오차(MSE), 평균 제곱근 오차(RMSE), 평균 절대 오차(MAE) 및 결정 계수(R2)이다.

Type of Metrics

Mean Squared Error (MSE)

Definition:
평균 제곱 오차(MSE)는 예측 값과 실제 값 간의 제곱 차이의 평균이다.
제곱 과정으로 인해 더 큰 오류에 더 큰 비중을 둔다.

Formula:
$\text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y_i})^2$

Interpretation(해석):

• 낮은 MSE는 더 나은 성능을 나타낸다.
• MSE는 큰 오류가 제곱되기 때문에 이상값에 민감하다.

Use Case:
MSE는 큰 예측 오류를 더 크게 벌주고자 할 때 유용하며, 큰 예측 오류가 특히 바람직하지 않은 응용 분야에 적합하다.

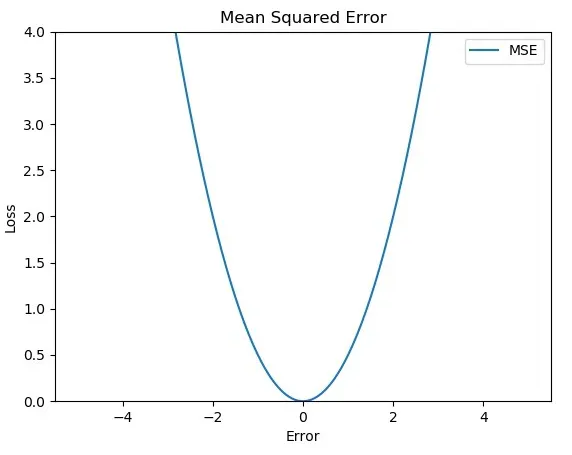
• 오류 값이 제곱되기 때문에, 오류가 0과 1 사이일 때는 오류가 원래 값보다 작게 반영되고, 오류가 1보다 클 때는 원래 값보다 크게 반영된다.

• 모든 함수 값은 미분 가능하다. MSE는 이차 함수이기 때문에 최고점을 가지지 않는다.

Root Mean Square Error (RMSE)

Definition:
평균 제곱근 오차(RMSE)는 예측 값과 실제 값 간의 제곱 차이의 평균의 제곱근이다.

Formula:
$\text{RMSE} = \sqrt{ \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y_i})^2 }$

Interpretation:

• RMSE는 종속 변수와 동일한 단위(제곱X) 로 직접 해석할 수 있다.
• 낮은 RMSE는 더 나은 성능을 나타낸다.
• MSE와 마찬가지로 RMSE는 이상값에 민감하다.

Use Case:
RMSE는 해석하기 쉽고 종속 변수의 규모와 직접적으로 관련된 오류 지표가 필요할 때 일반적으로 사용된다.
민감정도가 MSE와 MAE의 중간정도라서, 일반적인 문제에 많이 사용된다.

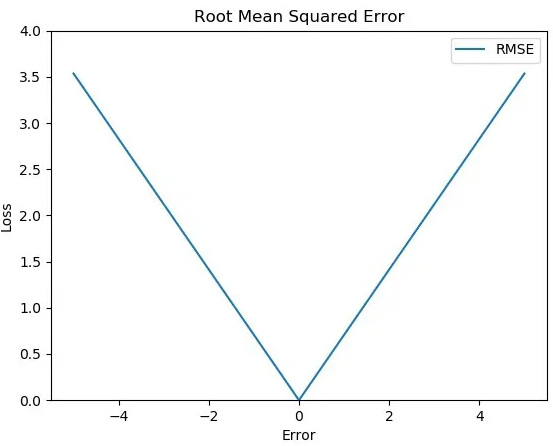
• MSE에서 제곱근을 취하기 때문에 오류가 증폭되는 MSE의 단점이 어느 정도 제거된다.
• MSE는 부드러운 곡선 형태로 오류 함수를 가지지만, RMSE는 MSE에서 제곱근을 취하기 때문에 미분 불가능한 점을 가진다.

Mean Absolute Error (MAE)

Definition:
평균 절대 오차(MAE)는 예측 값과 실제 값 간의 절대 차이의 평균이다. 이는 더 큰 오류를 강조하지 않는다.

Formula:
$\text{MAE} = \frac{1}{n} \sum_{i=1}^{n} | y_i - \hat{y_i} |$

Interpretation:

• MAE는 MSE 및 RMSE에 비해 이상값에 덜 민감하다.
• 낮은 MAE는 더 나은 적합성과 높은 예측 정확성을 나타낸다.

Use Case:
MAE는 오류의 크기에 관계없이 모든 오류를 동일하게 취급하는 간단하고 직관적인 예측 오류 측정이 필요할 때 유용하다.

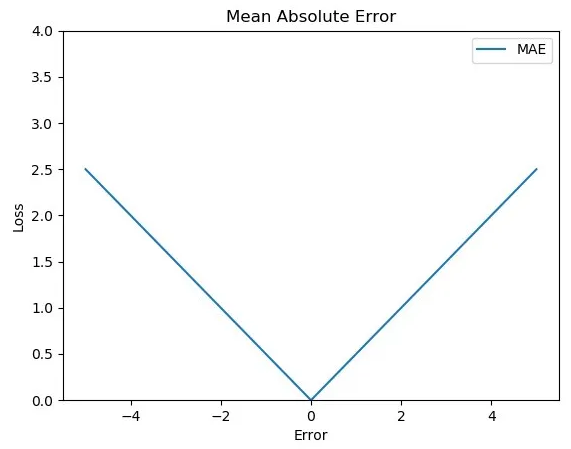
• 값이 제곱되지 않기 때문에 이상값에 대해 강건(민감하지 않음)하다.
• MAE를 나타내는 함수의 최소값이 꼭지점이기 때문에 함수 값 중 미분할 수 없는 점이 있다.
• MSE와 RMSE와 달리 모든 오류에 동일한 가중치를 부여한다.

RMSE vs MAE

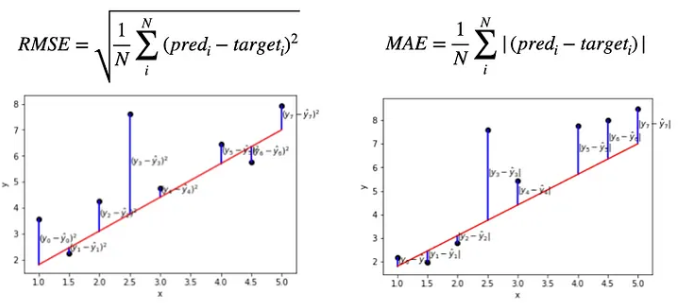
제곱하여 루트를 씌우는 RMSE는 큰값은 더 크게, 작은값은 더 작게 받아들여지는 경향이 있다.

결정 계수 (R²)

Definition:
결정 계수 (R²)는 독립 변수로부터 종속 변수의 분산 중 예측 가능한 비율을 측정한다.

Formula:
$R^2 = \frac{SS_{\text{res}}}{SS_{\text{tot}}}= 1- \frac{SS_{\text{error}}}{SS_{\text{tot}}}$

여기서:

• $SS_{\text{res}}$는 잔차 제곱합
• $SS_{\text{tot}}$는 총 제곱합

Interpretation:

• $R^2$는 0에서 1까지의 값을 가진다.
• $R^2 = 0$은 모델이 종속 변수의 분산을 전혀 설명하지 못함
• $R^2 = 1$은 모델이 종속 변수의 모든 분산을 설명함
• 높은 $R^2$ 값은 더 나은 모델 성능과 설명력을 나타냄

Use Case:
$R^2$는 모델의 전반적인 적합성을 이해하고 다양한 모델의 설명력을 비교하는 데 유용하다.

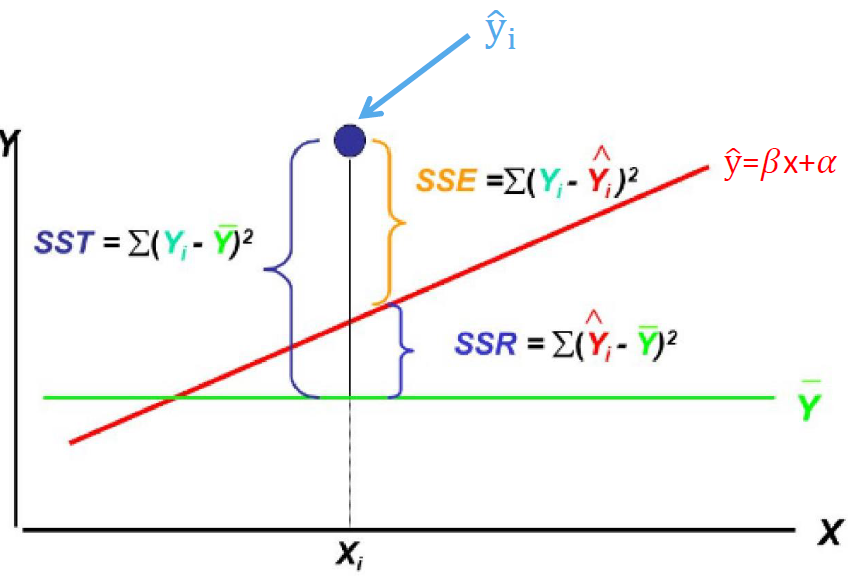
SST, SSR, SSE 간의 관계

$SST = SSR + SSE$
$\sum (y_i - \bar{y})^2 = \sum (\hat{y_i} - \bar{y})^2 + \sum (y_i - \hat{y_i})^2$

정의:
SST = 총 제곱합
SSR = 회귀에 의한 제곱합
SSE = 오류에 의한 제곱합

$R^2$는 회귀선(SSR)이 설명하는 총 변동(SST)의 비율이다.
$R^2 = \frac{SSR}{SST} = 1 - \frac{SSE}{SST}$
$(0 \leq R^2 \leq 1)$

값이 1에 가까울수록 회귀선의 설명력이 높다.

조정된 결정 계수 (R²)

• 조정된 결정 계수는($R^2$) 설명 변수가 추가됨에 따라 결정 계수가 증가하는 문제를 해결하기 위해 설계된 지표이다. 이는 모델 복잡성에 대한 패널티를 부과하여 모델이 훈련 데이터에 과도하게 맞춰져 새로운 데이터에 대한 예측 능력을 잃는 과적합을 방지한다.

• 조정 결정 계수는 SSE(잔차 제곱합)와 SST(총 제곱합)의 비율을 활용하여 조정된다. 여기서 n은 샘플 크기, k는 설명 변수의 수를 나타낸다. 이 비율은 자유도를 고려하여 조정되어 추가적인 설명 변수가 유의미한 개선을 가져오는지 더 정확하게 평가할 수 있게 한다.
  $R^2_{adj} = 1 - \left( \frac{SSE / (n - k - 1)}{SST / (n - 1)} \right)$

• 정의:

  • $R^2_{adj}$는 조정 결정 계수
  • SSE는 잔차 제곱합
  • SST는 총 제곱합
  • n은 샘플 크기
  • k는 설명 변수의 수

• 계수는 설명 변수가 추가될 때 반드시 증가하지는 않는다.

• 조정 결정 계수는 0과 1 사이의 값을 가지며, 값이 높을수록 데이터에 대한 모델 적합도가 더 좋음을 나타낸다.

• 그러나 높은 값이 반드시 좋은 모델을 의미하는 것은 아니다.

• 모델이 지나치게 복잡하면 과적합 문제가 발생할 수 있다.

• 따라서 모델을 평가할 때는 조정 결정 계수뿐만 아니라 다른 평가 지표도 고려하는 것이 중요하다.