Correlation

정의

• 상관 관계는 두 변수 간의 관계의 강도와 방향을 설명하는 통계적 측정치
• 두 변수가 상관 관계가 있을 때, 한 변수의 변화가 다른 변수의 변화와 연관이 있음을 의미

Types of Correlation

Positive Correlation

두 변수가 같은 방향으로 움직일 때. 하나가 증가하면 다른 것도 증가. 예를 들어, 키와 몸무게는 보통 양의 상관 관계를 보인다.

Negative Correlation

두 변수가 반대 방향으로 움직일 때. 하나가 증가하면 다른 하나는 감소. 예를 들어, 자동차 속도와 도착 시간은 음의 상관 관계를 보인다.

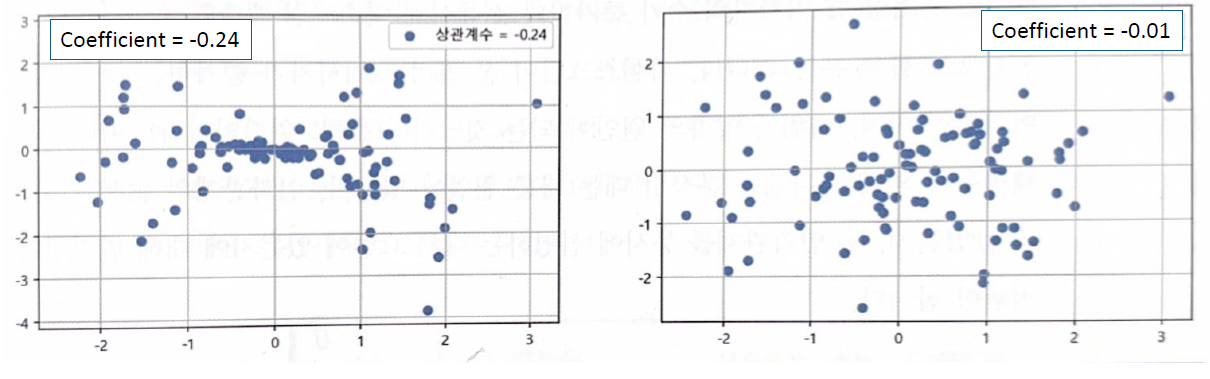
No Correlation

두 변수 간에 명확한 관계가 없을 때. 예를 들어, 무작위로 선택된 사람들의 커피 소비량과 수학 시험 점수 간에는 명확한 관계가 없다.

Measuring Correlation

• 상관 계수는 두 변수 X와 Y 간의 상관 계수 r을 계산하는 방법을 설명한다. 상관 계수는 두 변수 간의 선형 관계를 측정한다.
  $r = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum (x_i - \bar{x})^2 \sum (y_i - \bar{y})^2}}$

  • $x_i$와 $y_i$는 X와 Y의 관찰된 값
  • $\bar{x}$와 $\bar{y}$는 X와 Y의 샘플 평균
  • $n$은 관찰 횟수

• 공식은 분산과 표준 편차를 사용하여 다음과 같이 표현할 수도 있다
  $r = \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y}) / (n-1)}{\sqrt{\sum_{i=1}^n (x_i - \bar{x})^2 / (n-1)} \sqrt{\sum_{i=1}^n (y_i - \bar{y})^2 / (n-1)}} = \frac{\text{cov}(X,Y)}{SD_x \cdot SD_y}$

  • $cov(X, Y)$는 X와 Y의 공분산
  • $SD_X$와 $SD_Y$는 X와 Y의 표준 편차

• 이는 상관 계수가 공분산을 변수의 표준 편차의 곱으로 나눈 값임을 보여준다.

n-1로 나누는 이유는 샘플링 한 후의 평균이기 때문에(베셀 보정)

상관 관계와 공분산(Covariance)

상관 계수 r은 -1에서 1 사이의 값을 가진다.

• r = 1 : Perfect positive correlation
• r = −1 : Perfect negative correlation
• r = 0 : 상관 관계 없음.

공분산(Covariance)

• 공분산은 두 확률 변수의 변화가 함께 얼마나 변하는지를 측정하는 값이다.
• 이는 한 변수의 증가가 다른 변수의 증가(또는 감소)와 연관이 있는지를 결정한다.
• 공분산은 양수, 음수 또는 0이 될 수 있다.

양의 공분산

만약 cov(X,Y) > 0이면, X가 증가할 때 Y도 증가하는 경향이 있다.

• 마찬가지로 X가 감소할 때 Y도 감소하는 경향이 있다.

음의 공분산

만약 cov(X,Y) < 0이면, X가 증가할 때 Y는 감소하는 경향이 있으며 그 반대도 마찬가지이다.

0의 공분산

만약 cov(X,Y) = 0이면, 변수들 간에 선형 관계가 없음을 나타낸다. 그러나 이는 X와 Y가 독립적임을 의미하지는 않는다. 비선형 관계가 있을 수 있다.

• 공분산은 두 변수 간의 선형 관계의 방향에 대한 아이디어를 제공한다.
• 그러나 관계의 강도에 대한 정보는 제공하지 않으며, 이것이 상관 계수(r)의 역할이다.
• 상관 계수는 공분산을 변수의 표준 편차로 정규화하여 -1에서 1 사이의 단위 없는 값을 출력한다.

예시

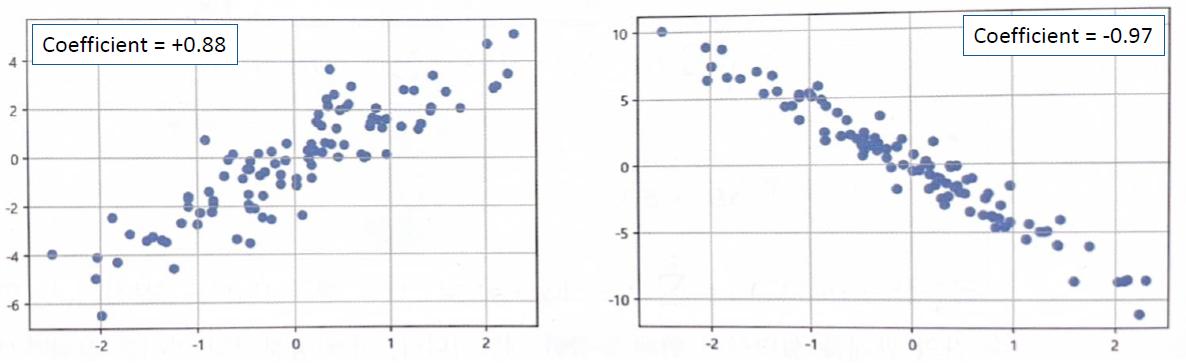
linear하지 않은 관계도 차원축소 등의 트릭을 통해 선형관계를 보여줄 수 있다.

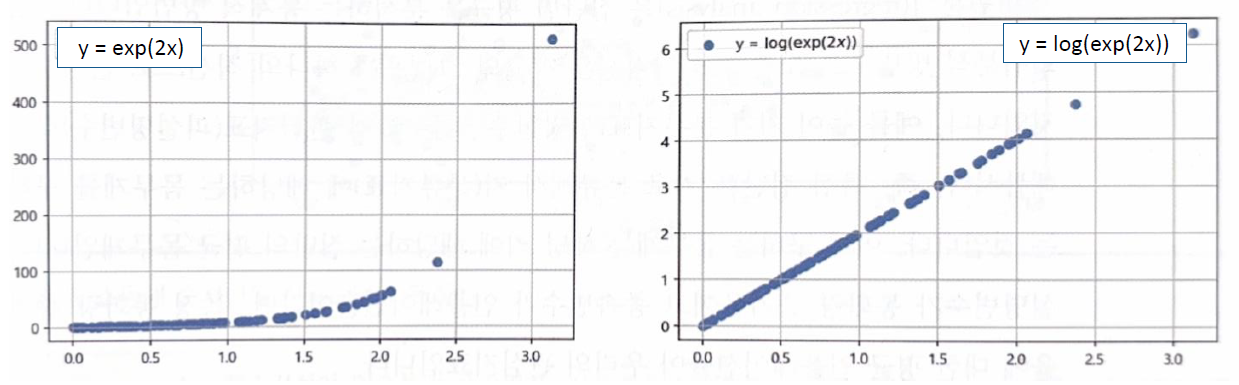
상관 관계 vs. 인과 관계(Causation)

• 두 변수 간의 상관 관계가 높더라도, 이것이 두 변수 간의 인과 관계를 의미하지는 않는다.

• 상관 관계는 두 변수 간의 선형 관계의 강도와 방향을 측정한다. 이는 한 변수가 변화할 때 다른 변수가 얼마나 변하는 경향이 있는지를 알려준다. 그러나 상관 관계는 인과 관계를 의미하지 않는다.

• 인과 관계(Causation)는 한 변수의 변화가 직접적으로 다른 변수의 변화를 일으키는 원인과 결과의 관계를 의미한다. 인과 관계를 확립하려면 일반적으로 통제된 실험이나 종단 연구가 필요하다. 이는 다른 요인을 배제하고 종속 변수의 변화가 독립 변수의 변화에 의한 것임을 의미한다.

예시

인과 관계 없는 상관 관계

• 아이스크림 판매량과 익사 사고
  아이스크림 판매량과 익사 사고 사이에 높은 상관 관계가 있다. 그러나 아이스크림을 먹는 것이 익사를 일으키지는 않는다. 기저 요인은 날씨로, 더운 날씨에 아이스크림 판매량과 익사 사고가 모두 증가한다.
• 이때 날씨-아이스크림판매량, 날씨-익사사고간에 인과관계가 있는 것

가짜 상관 관계

• 어린이의 신발 사이즈와 읽기 능력
  신발 사이즈와 읽기 능력 사이에 상관 관계가 있을 수 있지만, 신발 사이즈가 읽기 능력을 향상시키지는 않는다. 대신, 나이가 혼란 변수로 작용한다. 나이가 많은 어린이는 더 큰 발을 가지고 있고 더 많은 연습으로 인해 읽기 능력이 더 뛰어나다.

인과 관계를 확립하기 위한 방법

연구자들은 인과관계를 확립하기 위해 아래와 같은 방법을 활용한다.

• 무작위 대조 시험 (RCTs): 피실험자를 무작위로 실험군과 대조군에 배정하여 중재의 효과를 관찰한다.
• Longitudinal Studies(종단 연구) : 시간의 경과에 따라 피실험자를 추적하여 한 변수의 변화가 다른 변수에 미치는 영향을 관찰한다.
• 통계적 방법: 회귀 분석과 같은 기법을 사용하여 혼란 변수를 통제하고 인과 관계의 가능성을 결정한다.

Regression

• 회귀 분석은 종속 변수(보통 Y로 표시됨)가 독립 변수(보통 X로 표시됨) 중 하나의 변화에 따라 어떻게 변하는지를 이해하는 데 도움이 된다.
  다른 독립 변수들은 고정된 상태로 변수를 변화시킨다.

회귀 분석의 종류

1. Simple Linear Regression(단순 선형 회귀):

• 하나의 종속 변수와 하나의 독립 변수를 포함
• 변수 간의 관계는 직선(선형 관계)으로 모델링
• 일반적인 방정식의 형태는 다음과 같다
  $Y = \beta_0 + \beta_1X + \epsilon$
• 여기서 $\beta_0$는 절편, $\beta_1$는 기울기, $\epsilon$는 오차 항

2. Multiple Linear Regression(다중 선형 회귀):

• 여러개의 변수를 하나의 선형 함수로 모델링
• 일반적인 방정식의 형태는 다음과 같다
  $Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + \cdots + \beta_pX_p + \epsilon$
• 각 $\beta$는 다른 변수를 고정한 상태에서 해당 X가 한 단위 변화할 때 Y의 변화를 나타낸다.

3. Polynomial Regression(다항 회귀):

• 독립 변수 X와 종속 변수 Y 간의 관계가 n차 다항식으로 모델링되는 형태
• 일반적인 방정식의 형태는 다음과 같다
  $Y = \beta_0 + \beta_1X + \beta_2X^2 + \cdots - \beta_nX^n + \epsilon$

4. Logistic Regression(로지스틱 회귀):

• 종속 변수가 범주형일 때 사용된다 (예: 이진 출력).
• 독립 변수와 종속 변수의 로그 오즈(log-odds) 간의 관계가 선형으로 모델링
• 일반적인 방정식의 형태는 다음과 같다.
  $\log \left( \frac{P}{1 - P} \right) = \beta_0 + \beta_1X_1 + \beta_2X_2 + \cdots + \beta_pX_p$
• 여기서 P는 종속 사건이 발생할 확률
  

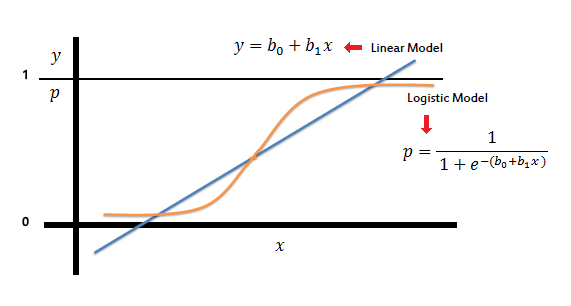
선형회귀 조건

1. 선형성:
   종속 변수와 독립 변수 간의 관계는 선형이어야 한다.
2. 독립성:
   관찰값은 서로 독립적이어야 한다.
3. 등분산성:
   잔차의 분산은 모든 독립 변수 수준에서 일정해야 한다.
4. 정규성:
   잔차는 대략 정규 분포를 따라야 한다.

선형 회귀 예제1

한국 통계청에서 수집한 가계 금융 복지 조사 자료에 따르면, 30대 1인 가구의 소득과 자산에 대한 평균, 표준 편차, 상관 계수는 다음과 같다.

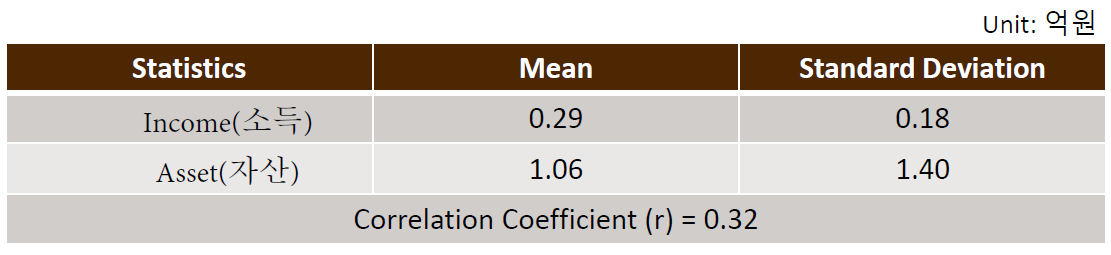
JACK의 소득이 상위 10%에 속한다고 가정할 때, JACK의 자산 백분위를 추정해보자.

풀이

1단계: 변수 정의

• Y: 자산
• X: 소득

2단계: 단순 선형 회귀 공식 사용

회귀 방정식은 다음과 같다
$Y = \beta_0 + \beta_1X$
$\beta_0$는 절편, $\beta_1$는 기울기

기울기 ($\beta_1$)는 상관 계수 (r)와 X 및 Y의 표준 편차를 사용하여 계산할 수 있다
$\beta_1 = r \cdot \frac{\sigma_Y}{\sigma_X}$

3단계: Calculate the Slope ($\beta_1$)

주어진 값:

• $r = 0.32$
• $SD_y = 1.40$ (자산의 표준 편차)
• $SD_x = 0.18$ (소득의 표준 편차)

$\beta_1 = r \cdot \frac{\sigma_Y}{\sigma_X}$

$\beta_1 \approx 2.4889$

4단계: Calculate the Intercept ($\beta_0$)

절편은 X와 Y의 평균을 사용하여 계산할 수 있다
$\beta_0 = \bar{Y} - \beta_1 \cdot \bar{X}$

주어진 값:

• $\bar{Y} = 1.06$ (자산 평균)
• $\bar{X} = 0.29$ (소득 평균)

$\beta_0 = 1.06 - (2.4889 \cdot 0.29)$

$\beta_0 \approx 1.06 - 0.7218$

$\beta_0 \approx 0.3382$

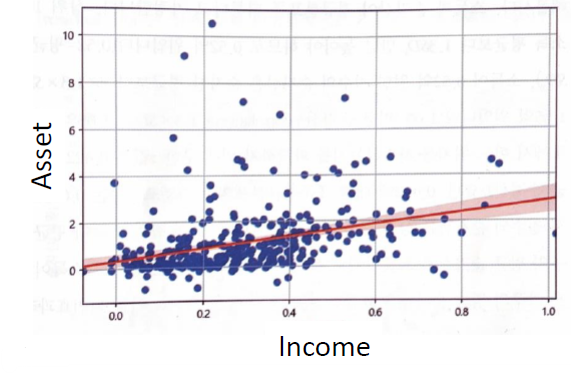
5단계 : 상위 10% 값 구하기

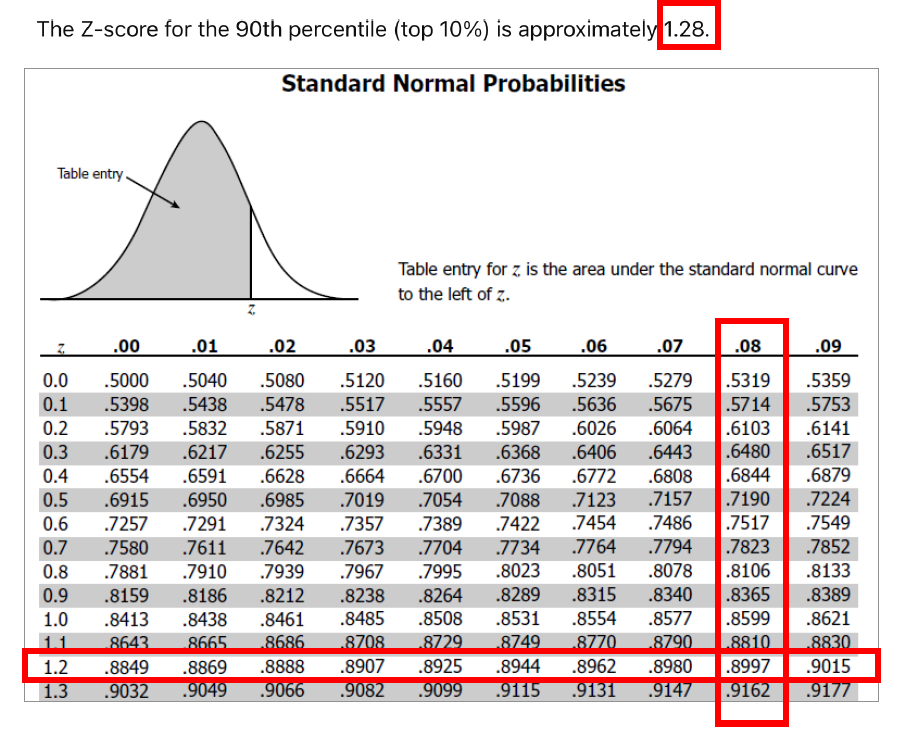
상위 10% 소득 수준에 대한 Z-점수는 약 1.28이다.

$X = \bar{X} + Z \cdot \sigma_x$

주어진 값:

• $\bar{X} = 0.29$ (소득 평균)
• $Z = 1.28$
• $\sigma_x = 0.18$

계산:

$X = 0.29 + 1.28 \cdot 0.18$
$X = 0.29 + 0.2304$
$X \approx 0.5204$

-> JACK의 소득은 대략 0.52 억원

Step 6: 상위 10% 소득에 대한 자산(순자산)을 추정

$Y = \beta_0 + \beta_1X$

주어진 값:

• $\beta_0 = 0.3382$
• $\beta_1 = 2.4889$
• $X \approx 0.5204$

계산:

$Y = 0.3382 + 2.4889 \cdot 0.5204$

$Y \approx 0.3382 + 1.2943$

$Y \approx 1.6325$

-> 상위 10%에 속할 때 그의 자산은 약 1.6325억 원으로 추정

Step 7: 상위 10% 소득에 대한 자산(순자산)이 상위 몇 프로인지 확인

주어진 값:

• 자산의 평균 ($\bar{Y}$) = 1.06
• 자산의 표준 편차 ($\sigma_y$) = 1.40
• 자산 값 ($Y$) = 1.63

Z-점수 공식:
$Z = \frac{Y - \bar{Y}}{\sigma_y}$
계산:
$Z = \frac{1.63 - 1.06}{1.40}$
$Z = \frac{0.57}{1.40}$
$Z \approx 0.4071$

Step 8: Find the Percentile

Z-표를 사용하여, Z = 0.4071에 해당하는 백분위수를 찾는다.

Z-표를 참조하면:

$P(Z < 0.4071) \approx 0.6578$

따라서, JACK의 자산은 하위 약 65.78%에 해당한다.

이로부터 백분위를 계산하면:

$1 - 0.6578 = 0.3422 \approx 34.22\%$

따라서, JACK의 자산은 상위 34.22%에 해당한다.

선형 회귀 예제2

대학 졸업생 그룹의 초봉과 학자금 대출 금액을 분석하고 있다.

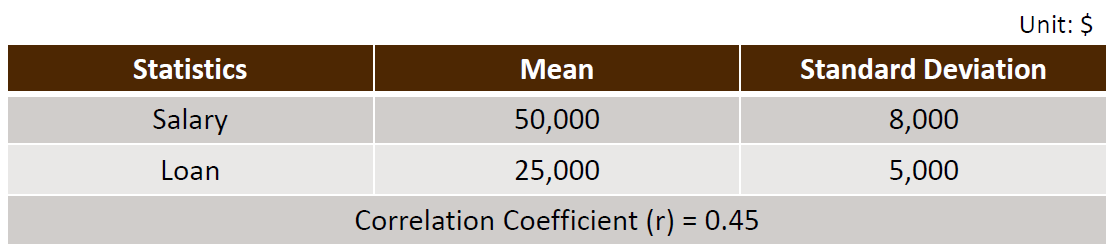
상위 5% 초봉에 해당하는 졸업생의 예상 학자금 대출 금액을 계산하자. 그리고 그 대출 금액에 해당하는 학자금 대출 분포의 백분위를 결정하여라.

풀이

1단계: 변수 정의

• Y: 학자금 대출 금액
• X: 초봉

2단계:

$Y = \beta_0 + \beta_1X$
$\beta_0$는 절편, $\beta_1$는 기울기

3단계: 기울기 ($\beta_1$) 계산

$\beta_1 = r \cdot \frac{\sigma_y}{\sigma_x}$

주어진 값:

• r = 0.45
• $\sigma_y$ = $5,000 (대출 표준 편차)
• $\sigma_x$ = $8,000 (초봉 표준 편차)

$\beta_1 = 0.45 \cdot \frac{5,000}{8,000}$
$\beta_1 = 0.45 \cdot 0.625$
$\beta_1 \approx 0.28125$

4단계: 절편 ($\beta_0$) 계산

$\beta_0 = \bar{Y} - \beta_1 \cdot \bar{X}$

주어진 값:

• $\bar{Y}$ = $25,000 (대출 평균)

• $\bar{X}$ = $50,000 (초봉 평균)

$\beta_0 = 25,000 - (0.28125 \cdot 50,000)$

$\beta_0 = 25,000 - 14,062.5$

$\beta_0 \approx 10,937.5$

5단계: 상위 5% 초봉 수준 결정

상위 5%에 해당하는 Z-점수는 약 1.645

$X = \bar{X} + Z \cdot \sigma_x$
주어진 값:
• $\bar{X} = 50,000$
• $Z = 1.645$
• $\sigma_x = 8,000$

$X = 50,000 + 1.645 \cdot 8,000$

$X = 50,000 + 13,160$

$X \approx 63,160$
상위 5%의 초봉은 약 $63,160이다.

6단계: 상위 5% 초봉에 대한 학자금 대출 금액 추정

$Y = \beta_0 + \beta_1X$
$Y = 10,937.5 + 0.28125 \cdot 63,160$
$Y = 10,937.5 + 17,760.25$

$Y \approx 28,697.75$

상위 5% 초봉의 학자금 대출 금액은 약 $28,697.75이다.

7단계: 학자금 대출 금액에 대한 Z-점수 계산

$Z = \frac{Y - \bar{Y}}{\sigma_y}$
주어진 값:

• $\bar{Y}$ = $25,000 (대출 평균)

• $\sigma_y$ = $5,000 (대출 표준 편차)

$Z = \frac{28,697.75 - 25,000}{5,000}$

$Z = \frac{3,697.75}{5,000}$

$Z \approx 0.73955$

8단계: 백분위수 찾기

Z-표 (또는 표준 정규 분포 계산기)를 사용하여 Z = 0.73955에 해당하는 백분위수를 찾는다.

$P(Z < 0.73955) \approx 0.7690$

76.69%

1-0.7669 = 0.2331 = 23.31%

따라서, 해당 대출 금액은 약 상위 23.31%에 속한다.