Shifter, Multiplier, Divider

Shifter, Rotator

bit를 이동시키고 2의 제곱수로 곱하거나 나누는 연산을 수행한다.

Logical Shifter : bit를 왼쪽 또는 오른쪽으로 이동시키고 생기는 빈 공간을 0으로 채운다.

• 11001 >> 2 = 00110
• 11001 << 2 = 00100

Arithmetic Shifter : logical shift와 동일하나, right shift에서만 생기는 빈 공간을 msb로 채운다.

• 11001 >>> 2 = 11110
• 11001 <<< 2 = 00100

Rotator : bit를 원형으로 순환시킨다. 즉, 밀려 나온 bit들은 반대쪽 끝으로 들어간다.

• 11001 ROR 2 = 01110
• 11001 ROL 2 = 00111

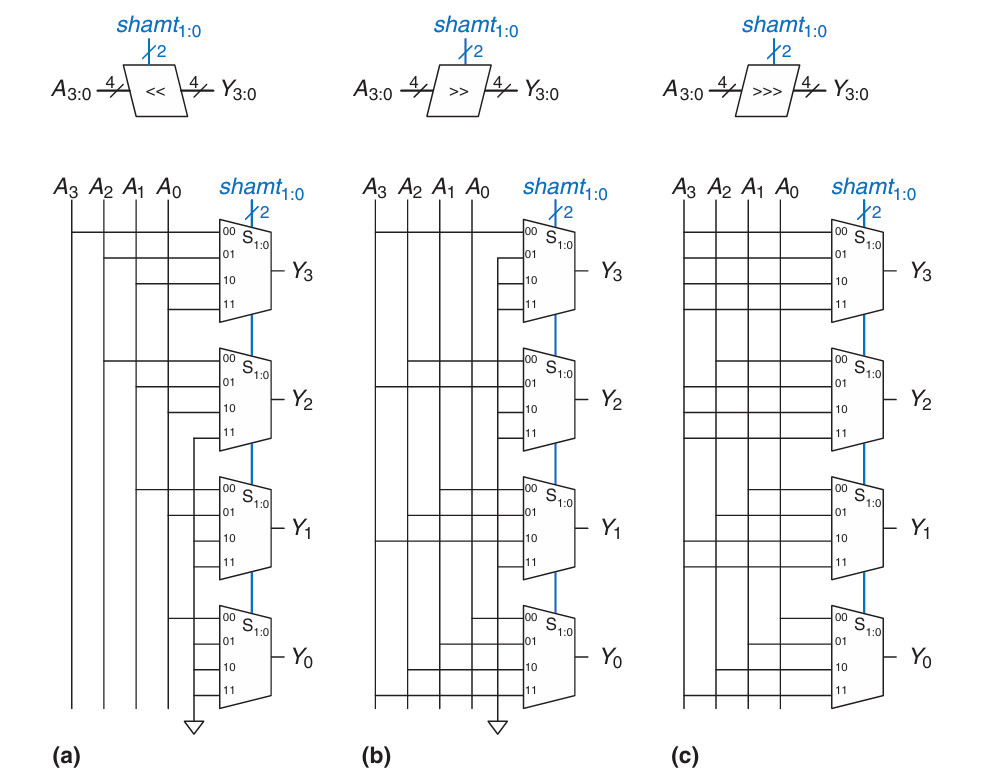
(a) shift left, (b) logical shift right, (c) arithmetic shift right

N-bit shifter는 N개의 N:1 mux로 설계된다.
(b)와 (c)의 차이를 보면 (b)의 경우 채워지는 자리에 0이 연결되어있는 것을 볼 수 있다. (c)의 채워지는 bit는 msb에 의해 결정되기 때문에 모든 자리에 $A_3$이 연결되어있다.

Shift연산과 곱셈/나눗셈의 관계

• $A<<N = A\times2^N$
• $A>>>N=A\div 2^N$

단, 나눗셈의 경우 피연산자가 양의 정수(unsigned이거나 signed int)이고 arithmetic shift이며 2의 거듭제곱으로 나누어 떨어지는 경우에만 성립함을 주의하자.

Multiplier

unsigned 이진수의 곱셈은 0과 1만을 사용한 정수 곱셈과 유사하다.

일반적으로 $N\times N$ multiplier는 두 개의 $N$-bit 이진수를 입력으로 받아 하나의 $2N$-bit 이진수를 출력으로 낸다.

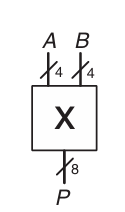
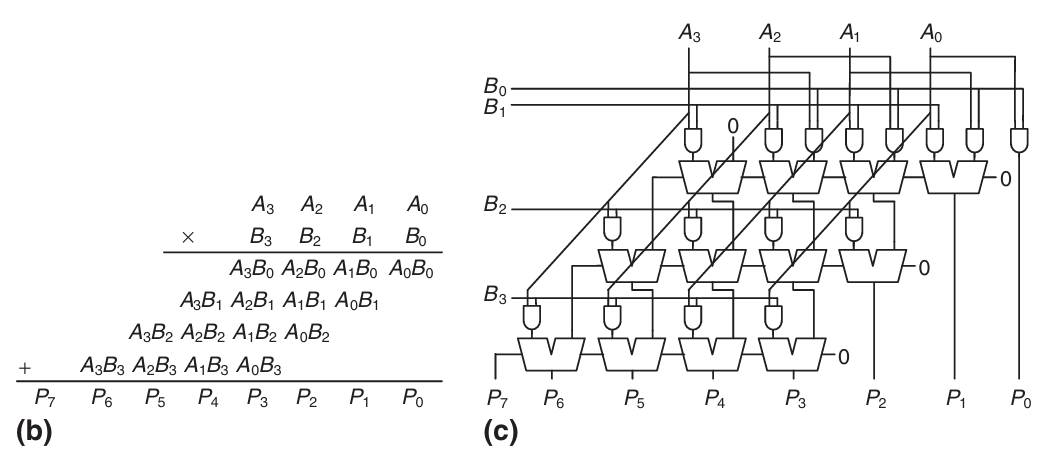
1-bit 이진수의 곱셈연산은 AND 연산과 같다.
(1×1=0, 1×0=0 ; 1 AND 1 = 1, 1 AND 0 = 0)
따라서 partial product 구현에는 AND gate가 사용된다.

각 partial product는 multiplier bit $B_3,B_2,B_1,B_0$와 multiplicand bit $A_3,A_2,A_1,A_0$의 AND 연산이다. 피연산자가 $N$-bit라면 $N$개의 partial product가 존재하고 $N-1$ 개의 1-bit adder 계층이 존재한다.

Divider

나눗셈은 다음과 같이 생각할 수 있다.

$A/B=Q+R/B$
$Q$ : 몫
$R$ : 나머지

2584/15=172 R4의 연산과정을 살펴보자.

이진수에서도 동일하게 수행이 가능하다.

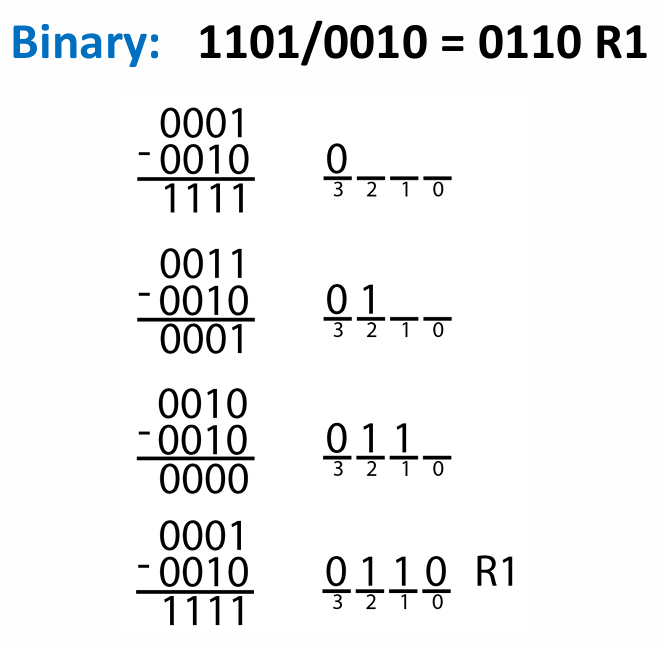
이 과정을 알고리즘화 하면 다음과 같이 작성된다.

$A/B=Q+R/B$

$R^{\prime}=0\\\mathsf{for}\ i=N-1\ \mathsf{to}\ 0\\\quad R=\{R^{\prime}<<1,A_i\}\\\quad D=R-B\\\quad \mathsf{if}\ D<0\ \mathsf{then}\ Q_i=0,\ R^{\prime}=R\;\;//\ R<B\\\quad \mathsf{else}\quad\quad\quad\quad\ \ Q_i=1, R^{\prime}=D\;\;//R\ge B\\R=R^{\prime}$

ⅰ) partial remainder $R$을 $R^{\prime}$으로 초기화한다.
ⅱ) $R$의 lsb를 $A$의 bit로 shift 한다(매 loop마다 msb부터 한자리씩).
ⅲ) $R < B$이면 결과는 0이고 $R^{\prime}=R$로 초기화한다.
ⅳ) $R\ge B$이면 결과는 1이고 $R^{\prime}=D$로 초기화한다.
ⅴ) 위 과정을 자리수만큼 반복한다.
ⅵ) 마지막에 나머지 $R$은 $R^{\prime}$으로 정해진다.

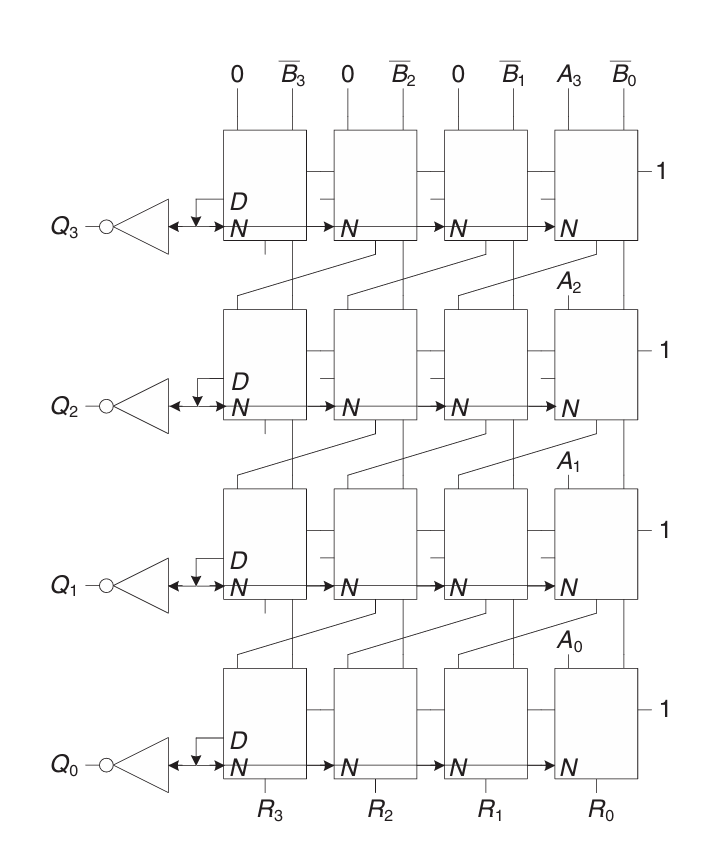
위 알고리즘을 토대로 설계한 4×4 Diveder다.

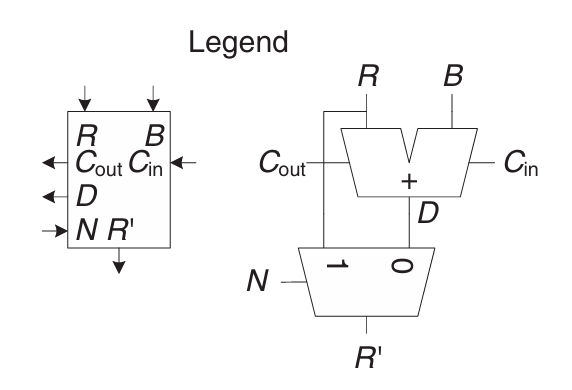
내부적으로는 위와 같이 설계되어있다.

---

<참고자료>
Harris & Harris, Digital Design and Computer Architecture, RISC-V Edition, 2022.