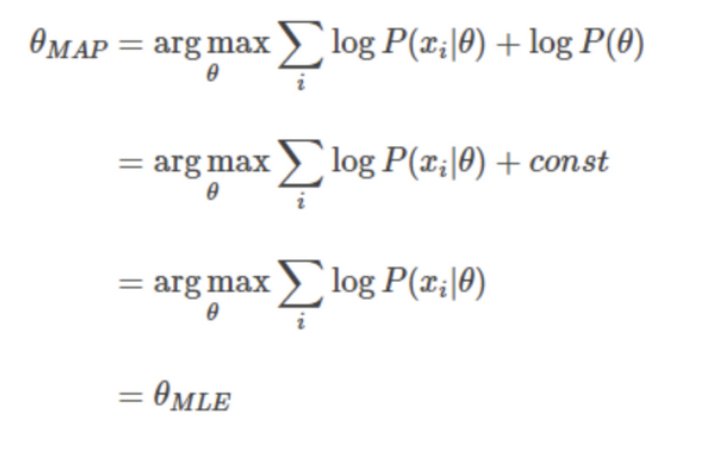MLE & MAP

MLE(Maximum Likelihood Estimation)

---

• Likelihood 값을 최대로 하는 $\theta$를 찾는 방법
  $P(\theta|X) = {P(X|\theta)p(\theta) \over P(X)} \propto P(X|\theta)$
  ⇒ 여기서 posterior를 크게하는 것은 likelihood를 크게하는 것이라고 생각하는 방식이다.
  • $\theta_{MLE} = argmax_\theta P(X|\theta) = argmax_\theta \prod_iP(x_i|\theta)$ $\theta_{MLE} = argmax_\theta \log \prod_i P(x_i | \theta) = argmax_\theta \sum_i \log P(x_i|\theta)$
    

MAP(Maximum A posterior Probability)

---

• Posterior probability를 최대로 하는 $\theta$를 찾는 방법
  $P(\theta|X) = {P(X|\theta)p(\theta) \over P(X)} \propto P(X|\theta)p(\theta)$
  ⇒ $P(X|\theta)P(\theta)$값을 최대로하는 $\theta$를 찾는 것

  • $\theta_{MAP} = argmax_{\theta} P(x|\theta)P(\theta) = argmax_\theta [\log P(X|\theta) + \log P(\theta)]$

    $= argmax_{\theta} \log \prod_iP(x_i | \theta) + \log P(\theta) = argmax_{\theta} \sum_i\log P(x_i|\theta) + \log P(\theta)$
    

Uniform Distribution

---

• 만약 $\theta$가 uniform distribution일 경우, $P(\theta)$는 상수가 되기 때문에 MLE = MAP가 된다.