SVM(Support Vector Machine)

KAIST 문일철 교수님의 인공지능 및 기계학습 개론1 수업을 참고하여 정리한 글입니다.
https://www.edwith.org/machinelearning1_17/lecture/10602

1. SVM이란?

데이터를 두 범주로 나누는 문제를 푼다고 생각해 보자.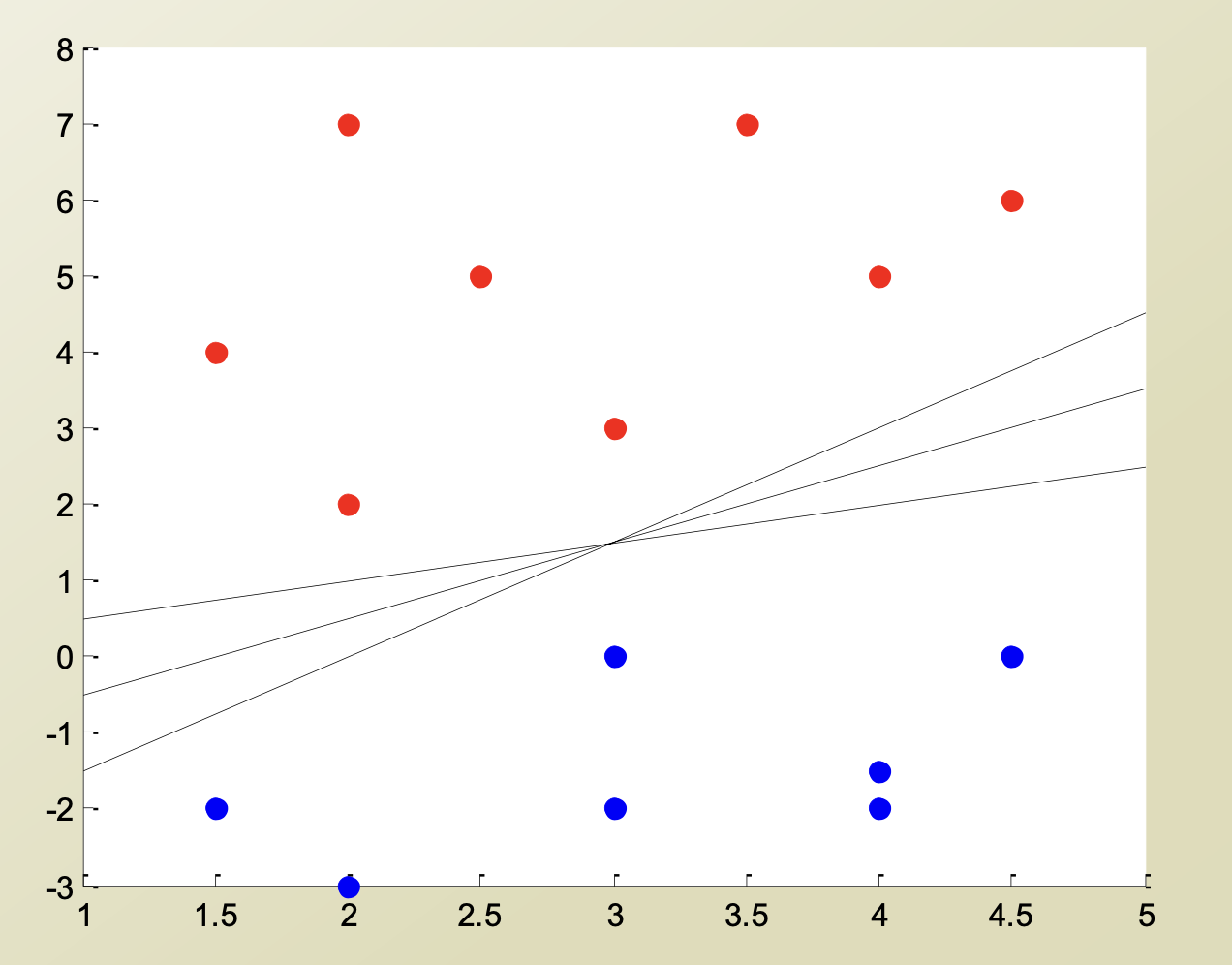이와 같이 데이터가 존재할 때, 데이터를 두 범주로 나누는 선은 어떻게 정의되어야 할까?
SVM은 이 경계선을 정의하는 모델이다.
여기서 경계선은 Decision Boundary 라고 한다.

2. Decision Boundary

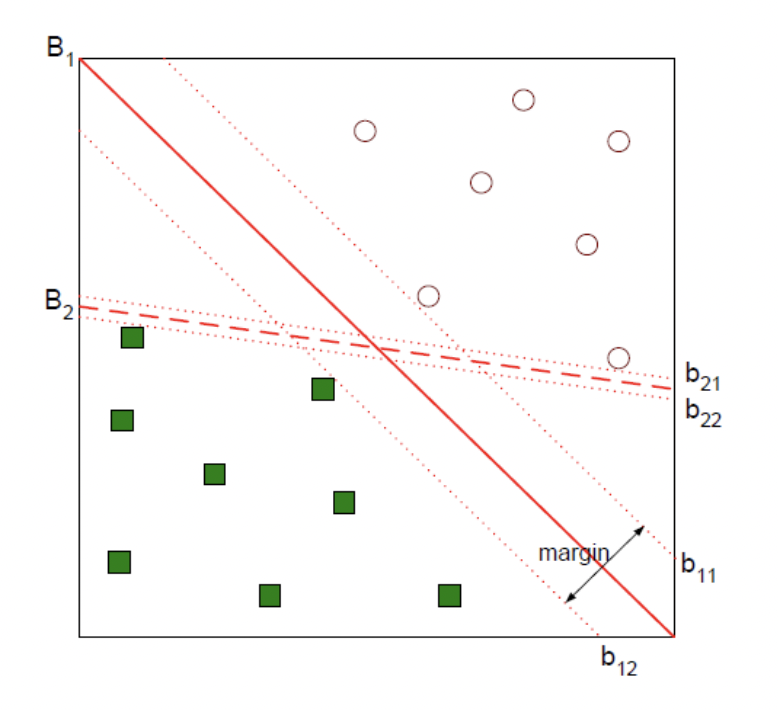위와 같이 데이터가 분포할 때, 데이터를 두 범주로 나누는 Decision Boundary는 여러가지가 존재한다. 그 중 두가지를 뽑아서 B1, B2로 나타냈는데, 둘 중 어느 것이 Decsion Boundary를 잘 설정했냐고 한다면, B1일 것이다.

그 이유는 그림과 같이 B1에 평행하면서 Decision Boundary 와 가장 근접해 있는 데이터와 맞닿은 선을 b11, b12라고 하고, 두 선 사이의 거리를 margin 이라고 정의했을 때, margin이 커지도록 Decision Boundary를 설정하는 것이 좋기 때문이다.

3. Margin Distance

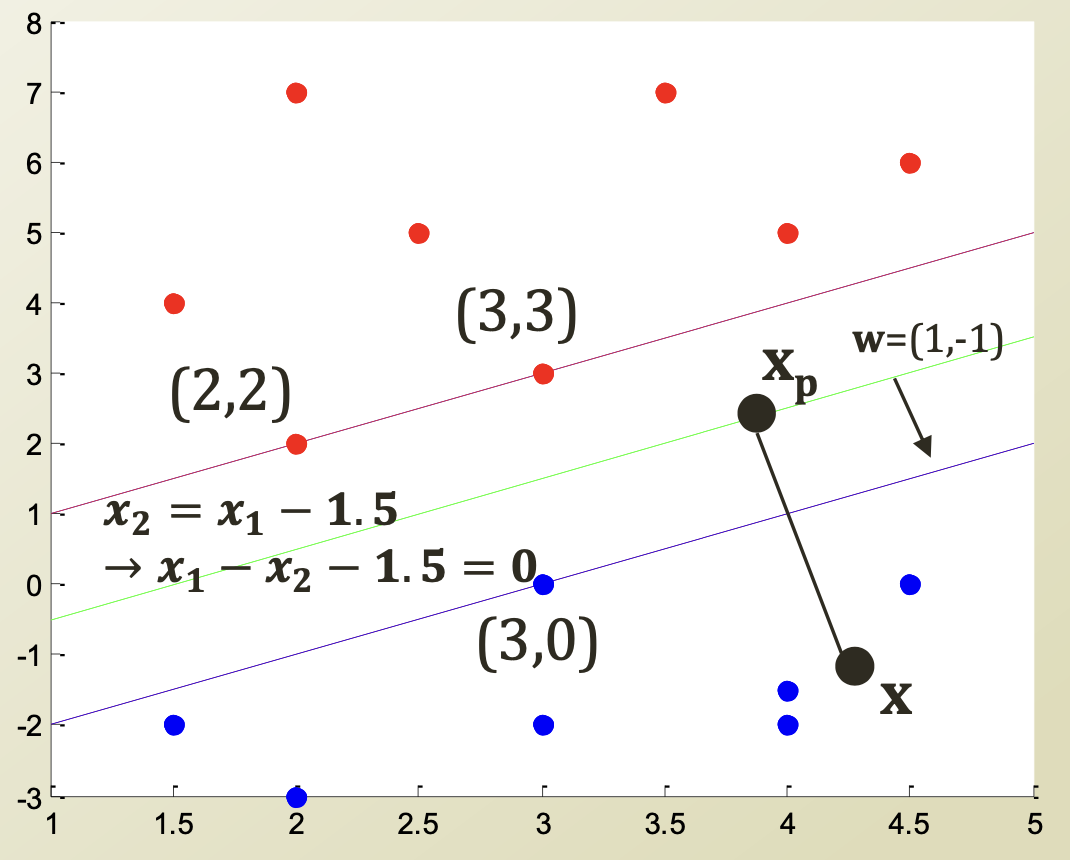Decision Boundary에 해당하는 직선 함수를 $f(x) = w \cdot x + b$ 라고 할 때,

• A point $x$ on the boundary
  $f(x) = w\cdot x + b = 0$
• A positive point x
  $f(x) = w \cdot x + b = a, a>0$

$x$ 가 $x_p$ 로부터 decision boundary에 수직하게 떨어져 있는 point라 할 때,
$x = x_p + r {w\over { ||w||}}$ 로 나타낼 수 있으며, $f(x_p) = 0$ 이다.
$f(x) = w \cdot x + b = w(x_p + r {w\over||w||}) + b=wx_p + b + r{w\cdot w \over ||w||}= r||w||$ $(\because f(x_p) = w \cdot x_p + b = 0)$
따라서, $x$ 부터 $x_p$까지의 distance인 $r={f(x) \over ||w||}$ 이다.

이제 distance 식을 도출했으니, margin distance를 구해보자.
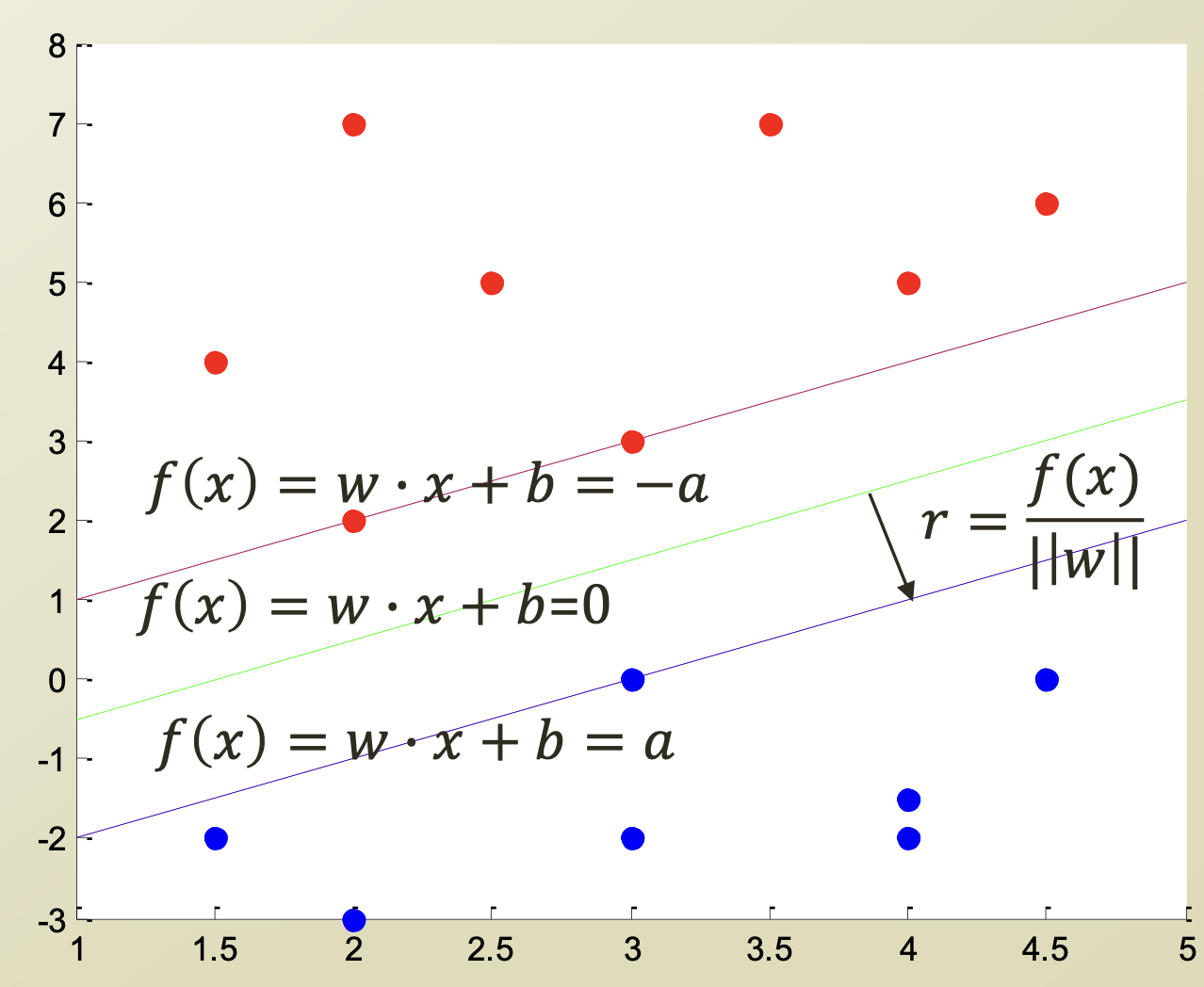Decision boundary가 위와 같을 때, margin distance는 $2r$ 이므로,
margin distance $= {2a \over ||w||}$ 이다.

margin distance이 최대가 되도록 하기 위해서 해결해야 하는 optimization problem은 다음과 같다.
$max_{w,b}2r = {2a \over ||w||}$
결국 해결해야할 optimization problem은 $min_{w,b}||w||$ 로 나타낼 수 있다.

4. Error cases in SVM

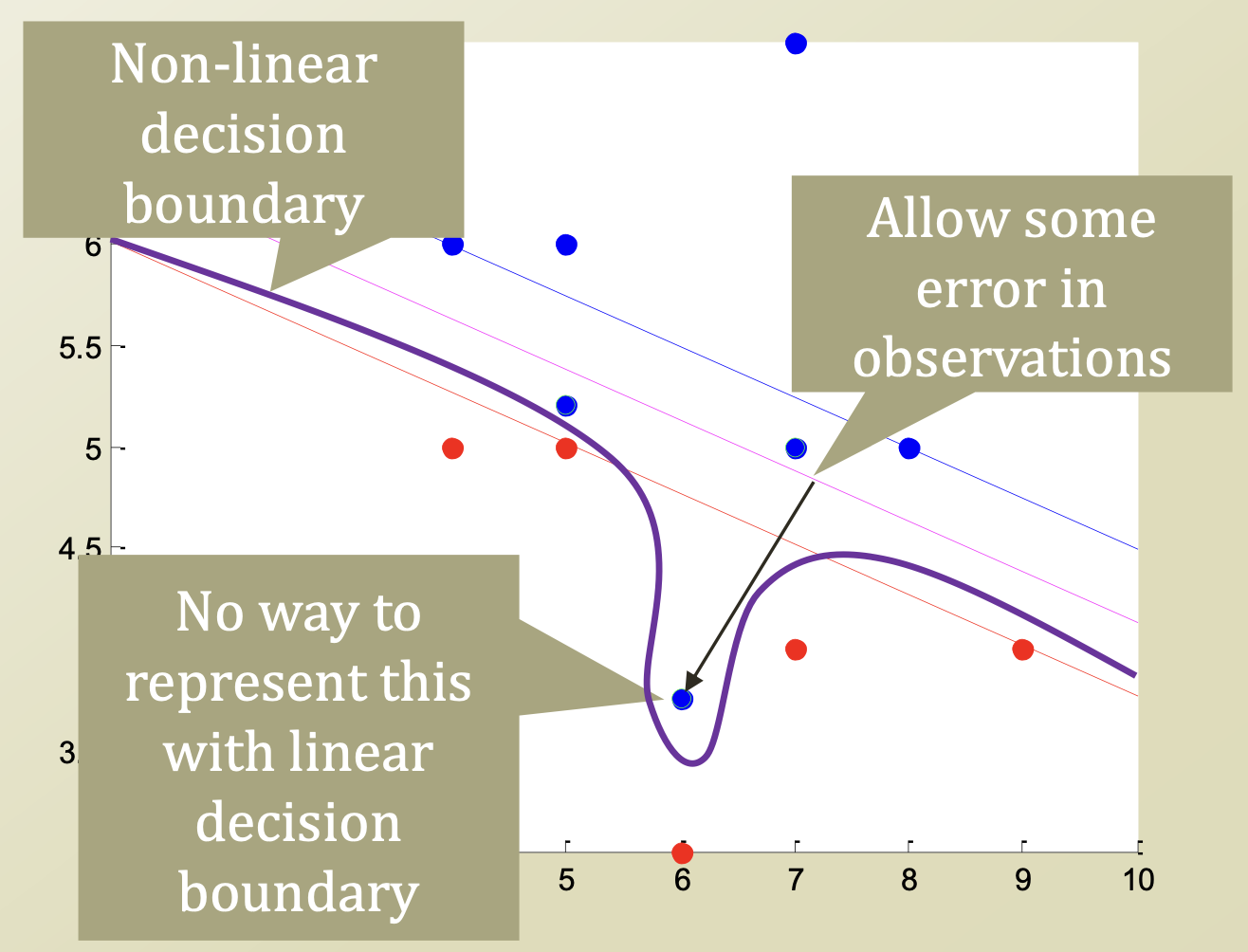=> 이와 같이 error case가 존재할 때, 이를 어떻게 해결해야할까?

• Option 1
  Make Decision Boundary more complex
  => non linear한 Decision boundary로 다시 설정함.
• Option 2
  Admit there will be an "error"
  => error data로 인정하고, 그에 대해 penalty를 부과함.

Error Handling in SVM

• Option 1 : Error case의 갯수를 세어, 그 수만큼 페널티를 부과함.
  $min_{w,b}||w||+ C \times \#_{error}$

• Option 2 : Error case가 Decision boundary로부터 얼마나 떨어져 있는지에 따라, 페널티를 다르게 부과함.
  $min_{w,b}||w||+ C \sum_j\xi_j$
  ($\xi$ = slack variable : Loss function)
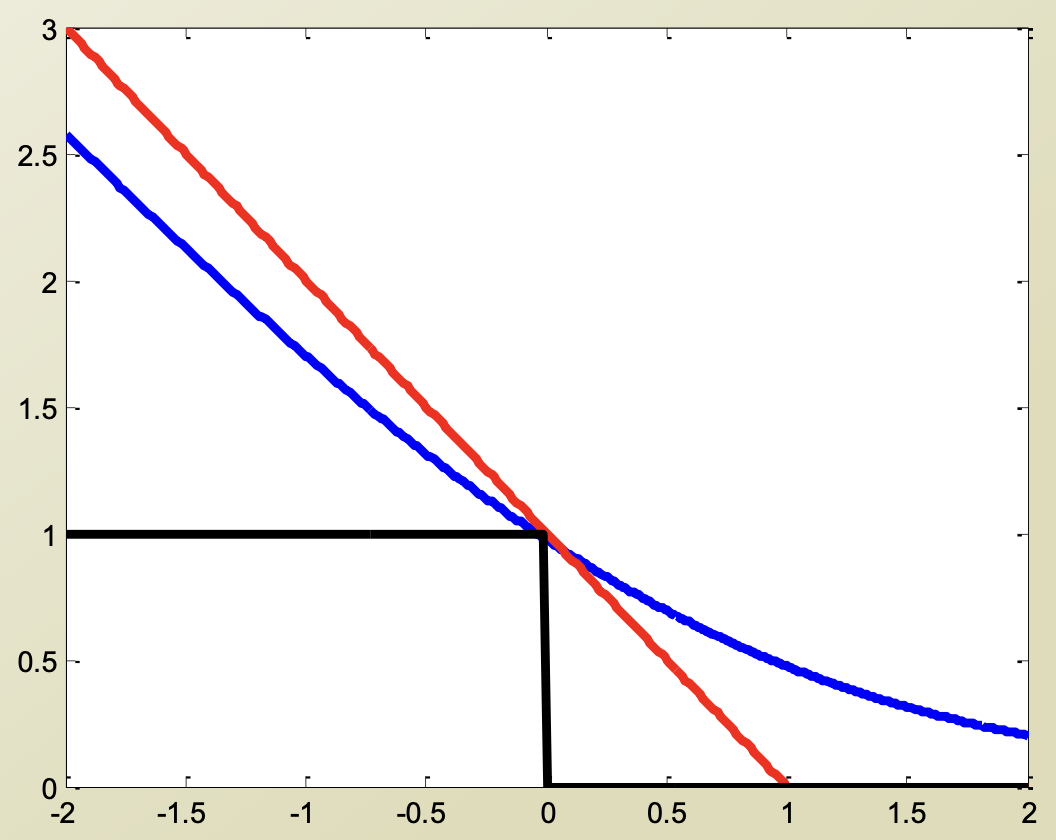
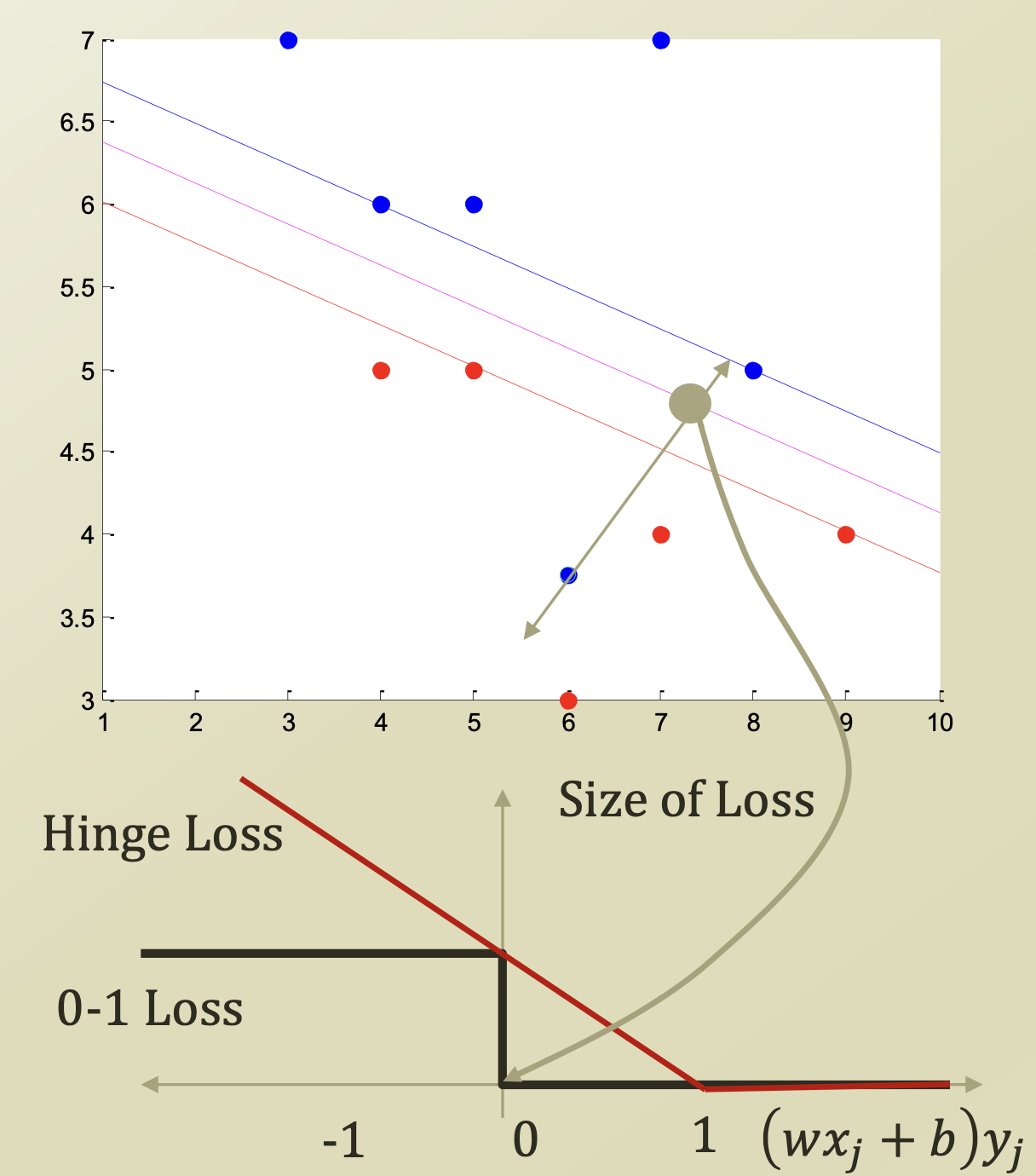  0-1 Loss의 경우 Option 1과 같이 Decision Boundary를 넘어가면 penalty가 1로 고정되는 것이고, Hinge Loss의 경우 Decision Boundary로부터 거리가 멀어질수록 penalty가 커진다.

• Loss function
  $\xi_j = (1 - (wx_j + b)y_j)_+$ => hinge loss
  $\xi_j = - log(P(Y_j|X_j, w, b)) = log(1 + e^{(wx_j + b)y_j})$ => log loss
  

5. Dual Problem of SVM

우리가 해결해야할 optimization problem은 다음과 같다.
$min_{w,b}||w||$
$s.t.$ $(wx_j + b)y_j\geq1, \forall j$

이 problem을 Lagrange Dual problem으로 바꾸면 다음과 같다.
$max_{\alpha \geq0} min_{w,b}{1\over2}w\cdot w - \sum_j\alpha_j[(wx_j + b)y_j -1]$
$s.t.\alpha_j\geq0, for$ $\forall j$
(Lagrange Dual Problem에 관해서는 다음 post에서 설명하겠습니다.)

여기서 strong duality를 만족하기 위해서 KKT Condition을 만족해야하므로,
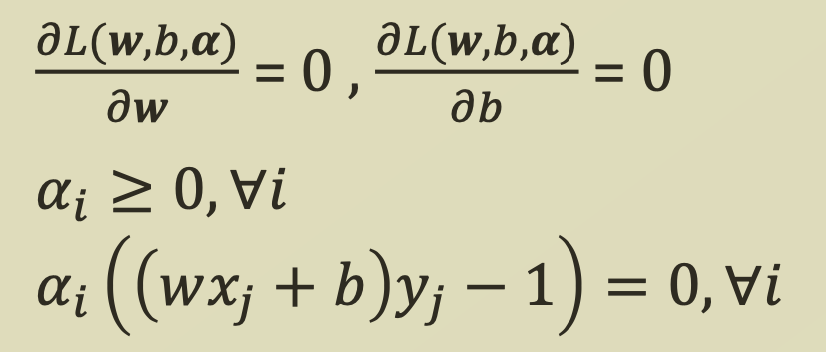위 식들을 함께 정리해보면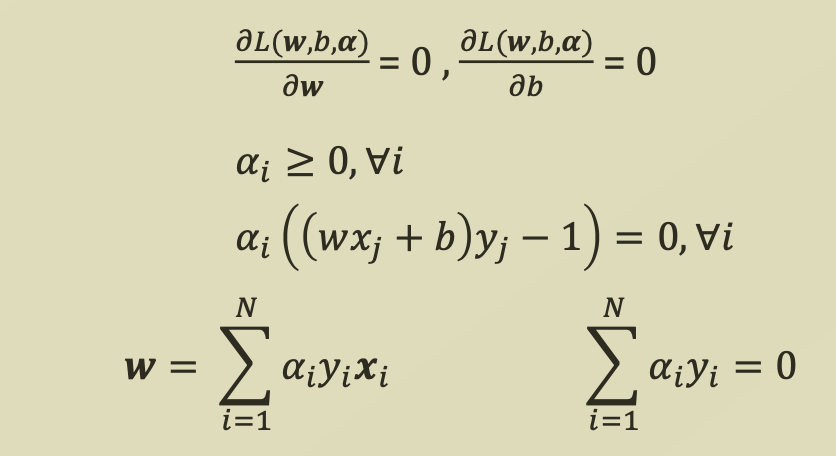다음과 같은 조건들을 도출할 수 있다.

이 조건들을 통해 Lagrange problem을 정리해 보면, 다음과 같이 정리된다.
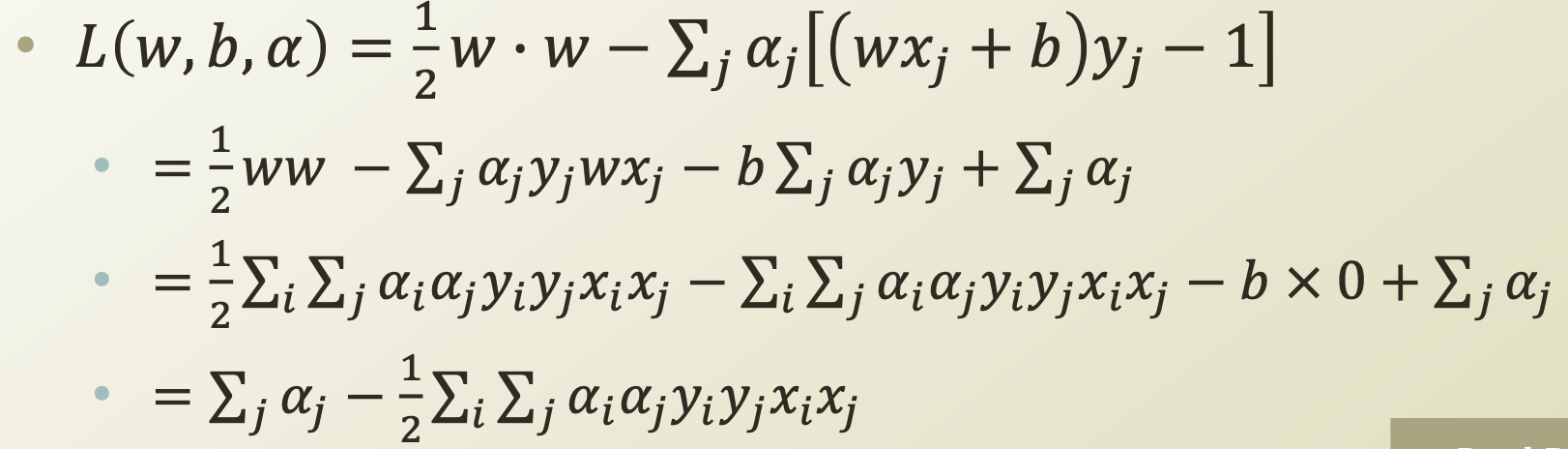=> 이 식은 $w$에 관한 식이 $\alpha$에 관한 식으로 변경되었다는 점에서 의의가 있다.

6. Kernel Trick

=> non-linear한 Decision boudary를 더 쉽게 설정하기 위해 하는 trick이다.

• Mapping Function
  => Linearly separable하지 않은 data들에 대해서, 더 높은 차원의 data로 mapping시킴으로써, linearly separable하도록 만드는 함수
  

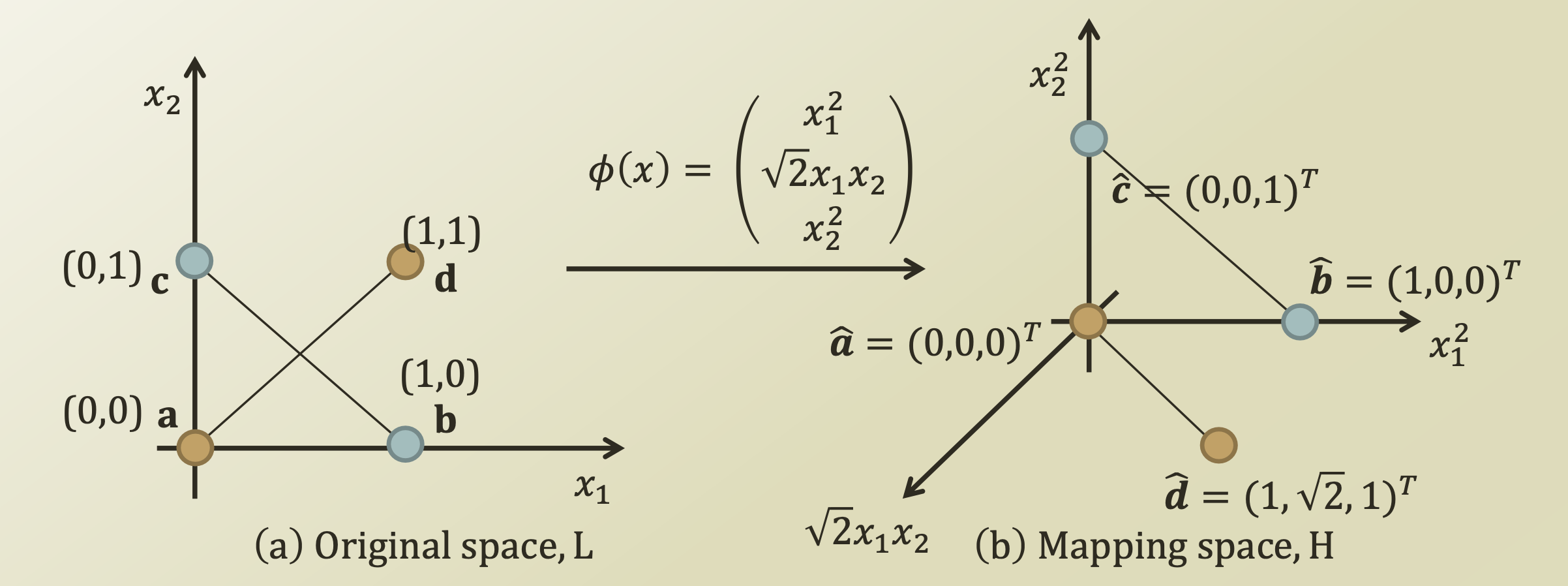
• Kernel Function
  => 두 data를 mapping function을 통해 다른 차원으로 보낸 후 내적한 것
  $K(x_i, x_j) = \phi(x_i)\cdot\phi(x_j)$

  예를 들어, $\phi(x) = (x_1^2, \sqrt2 x_1x_2, x_2^2)$ 라고 할 때, Kernel function으로 나타내 보자.
  $\textbf{x} = <x_1, x_2>$, $\textbf{z} = <z_1, z_2>$
  $K(<x_1, x_2>,<z_1,z_2>) =$
  $<x_1^2, \sqrt2 x_1x_2, x_2^2> \cdot <x_1^2, \sqrt2 x_1x_2, x_2^2>$
  $= (x_1z_1+x_2z_2)^2 = (\textbf{x} \cdot \textbf{z})^2$
  위의 식 처럼 복잡해보이는 두 mapping function을 내적함에 따라, 간단하게 나타낼 수 있다.

  위와 같은 Polynomial Kernel Function외에 다양한 kernel function이 있다.
  

7. Dual SVM with Kernel Trick

이제 SVM을 Dual problem으로 나타낸 식에 Kernel Trick을 적용해보자.
Data의 차원을 높이기 위해 mapping 시키면 다음과 같이 w와 b의 식을 정리할 수 있다.

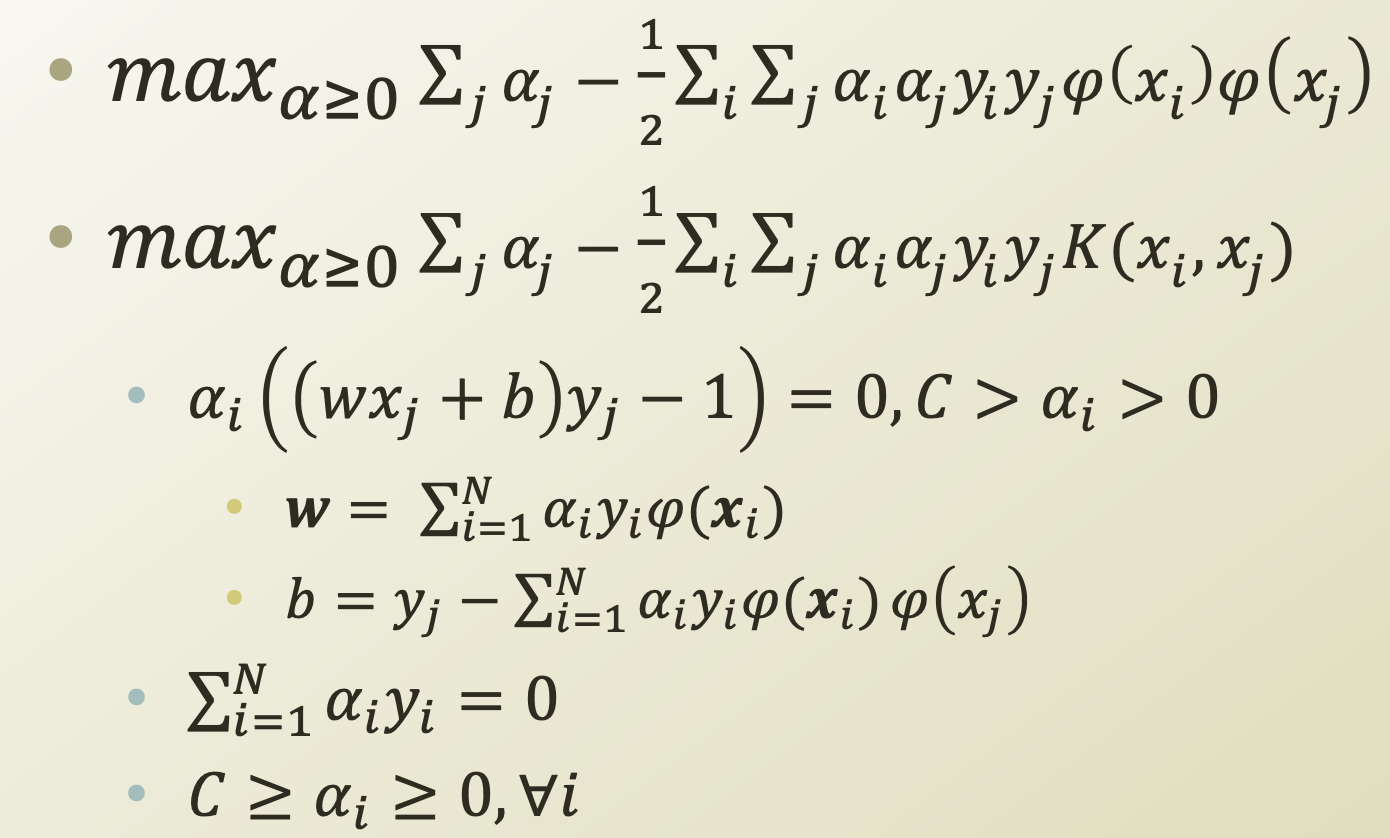
여기서 우리의 목적은 새로운 data가 들어왔을 때, Decision boundary식인 wx + b에 넣어 음수인지 양수인지 판단해 data를 분류하는 것이므로, 우리가 판단 해야할 식은 $sign(w\cdot x + b)$이다.

이 식에 커널 트릭을 적용하면 다음과 같다.

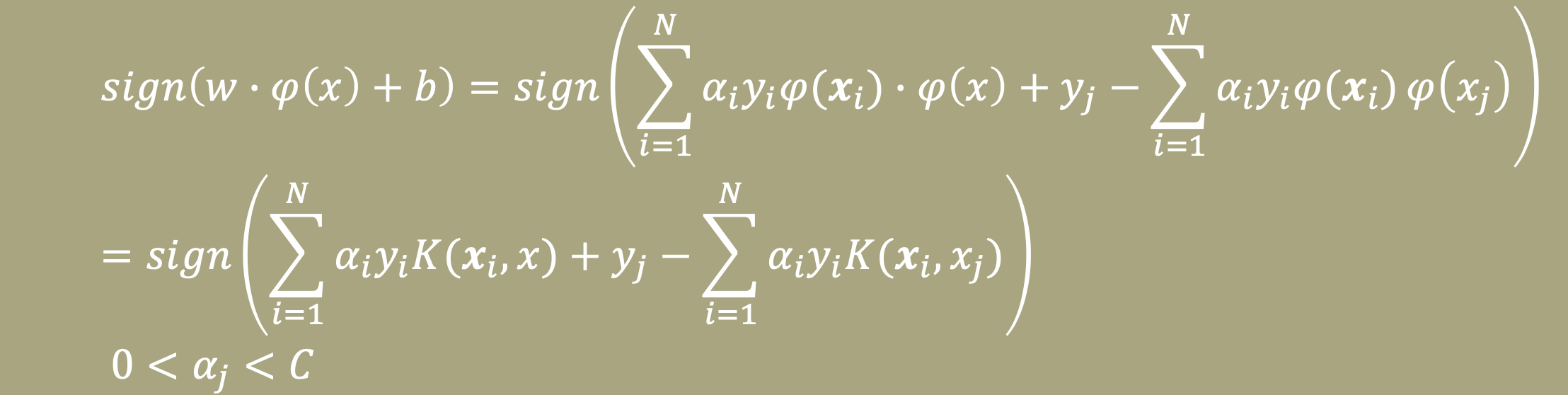
Reference

[1]https://ratsgo.github.io/machine%20learning/2017/05/23/SVM/
[2]https://hleecaster.com/ml-svm-concept/
[3]https://sanghyu.tistory.com/14