[cs231n] Lecture 3 : Loss function and Optimization

woonho·2022년 7월 19일

이 글은 cs231n(2017)강의를 보며 정리한 글입니다.
https://www.youtube.com/watch?v=h7iBpEHGVNc&list=PLC1qU-LWwrF64f4QKQT-Vg5Wr4qEE1Zxk&index=3

Loss function : 실제 데이터와 예측 데이터의 차이를 수치화 해주는 함수
=> 오차가 클수록 손실 함수의 크기가 커지므로, 손실함수의 크기를 최소화 시키는게 학습 목표가 된다.
Optimization : 손실 함수의 크기를 최소화 시키기 위한 가중치와 bias를 찾는 과정

1. SVM Loss

예를 들어, 이와 같이 각 데이터에 대한 score가 주어졌을 때, 각 데이터의 Loss값은 어떻게 정의될까?
Loss function에는 여러가지가 존재하지만, 이번 강의에서는 multiclass svm loss를 선택한다.
SVM Loss 식은 아래와 같다.
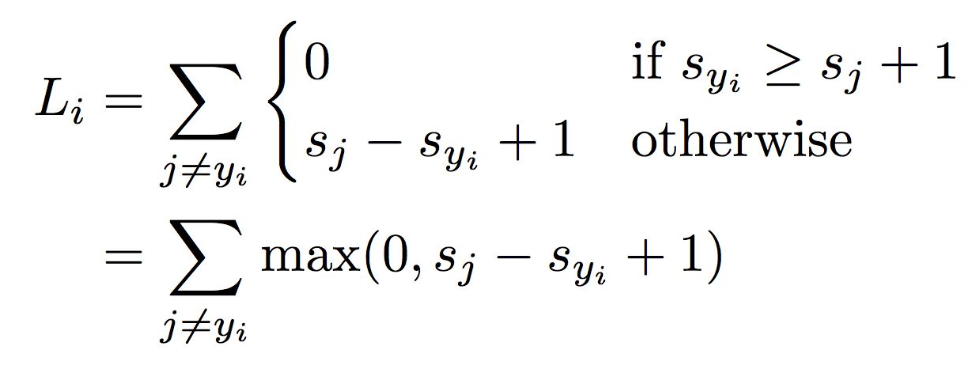이를 그래프로 나타내면
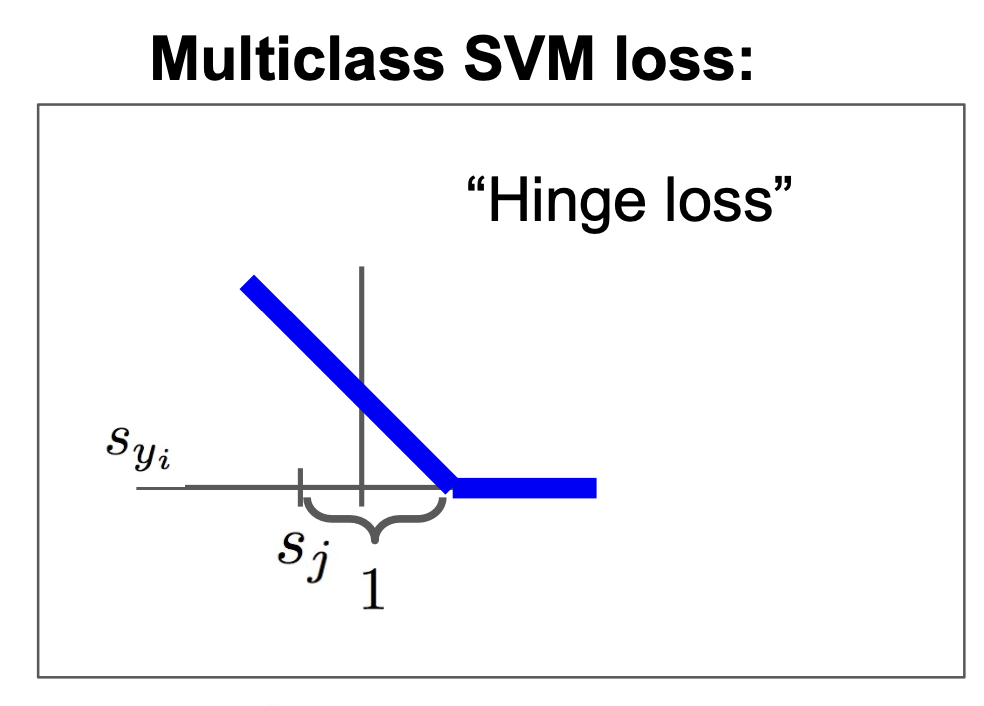다음과 같이 나타낼 수 있다.(이러한 함수를 Hinge loss라고 한다)
또한, 각 데이터의 Loss를 구해서 평균 내면 전체 데이터의 Loss를 구할 수 있다.
$L = {1\over N}\sum^N_{i=1}L_i$

따라서, 최종적으로 나타내면 다음과 같은 식으로 정리 된다.

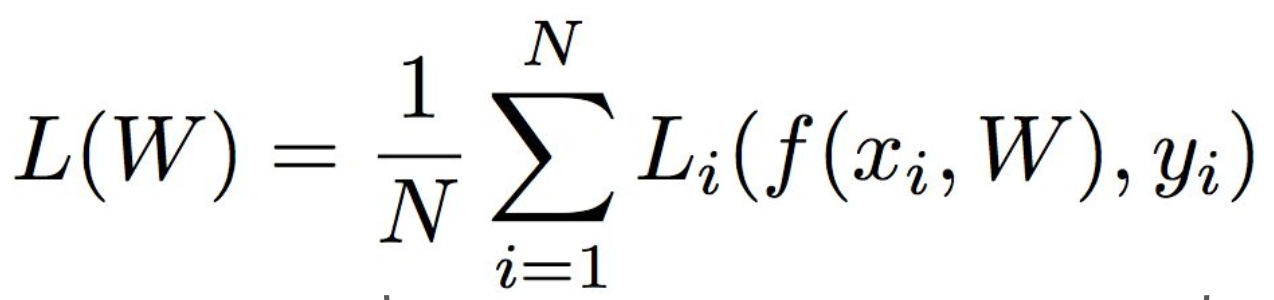
2. Regularization

하지만 여기서 Loss = 0이 된다고 해서, 학습이 잘된 것일까?
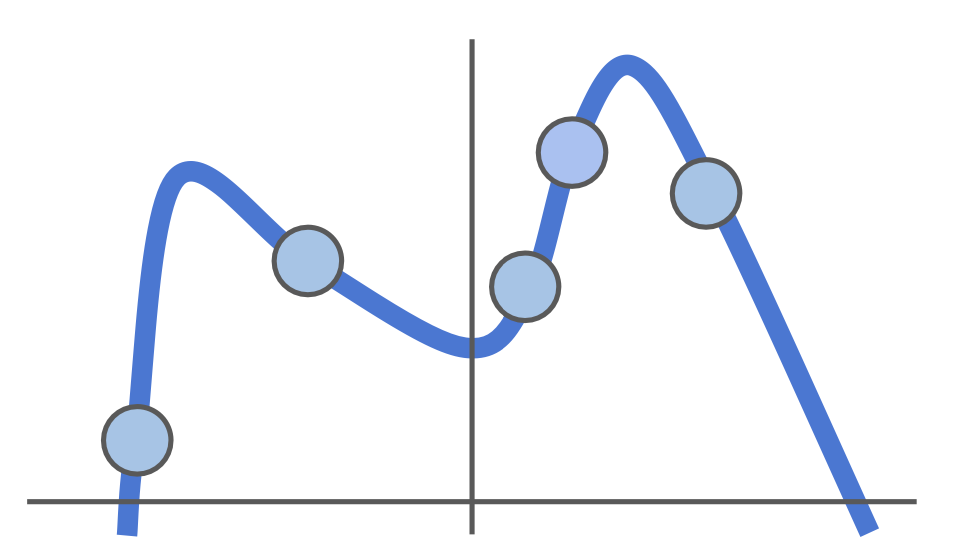데이터가 이와 같이 주어졌을 때, regression을 위와 같이 수행하면, 모든 데이터에 들어맞으므로, Loss = 0이다.

하지만, 또 다른 데이터가 아래와 같이 주어졌을 때, 이전에 구한 regression 식으로는 다른 데이터에 대해 설명하기가 어렵다.
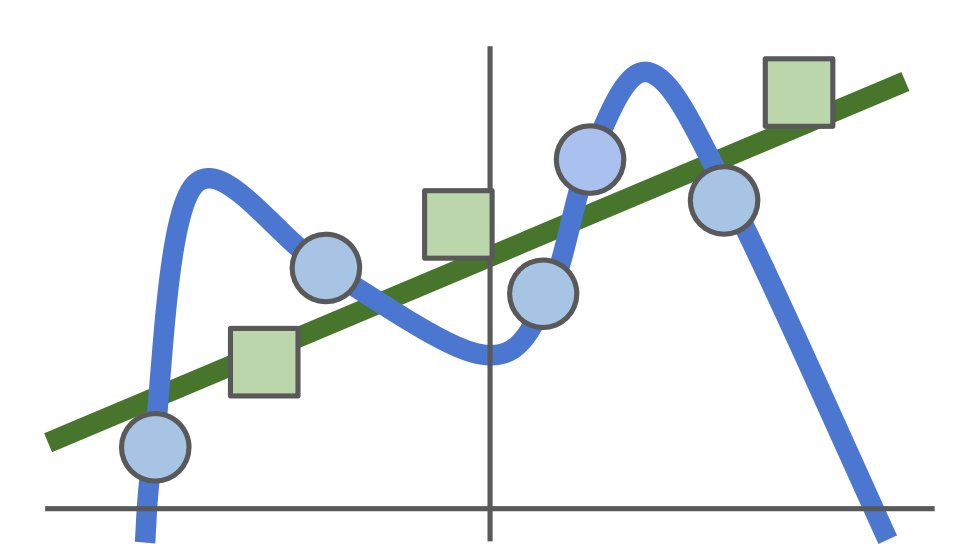따라서, 초록색 선과 같이 simple한 regression을 수행하는 것이 파란색 데이터에 대해서는 Loss가 있더라도, 새로운 데이터에 대해서는 더 좋은 regression 식이 될 수 있다.
(=> 이와 같이 training data에만 잘 들어맞고, test data에서는 오히려 정확도가 떨어지는 현상을 Overfitting이라고 한다.)
그래서 loss function을 더 simple하게 해주기 위한 과정을 Regularization이라고 한다.

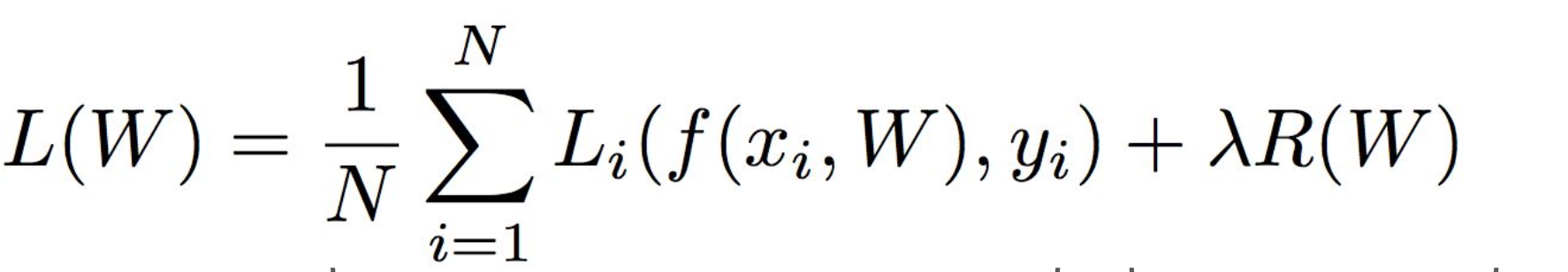
=> 여기서 람다는 regularization strength를 나타내는 hyperparameter이며, R(w)는 regularization 식을 나타낸다.

Regularization function
L1 regularization과 L2 regularization의 차이

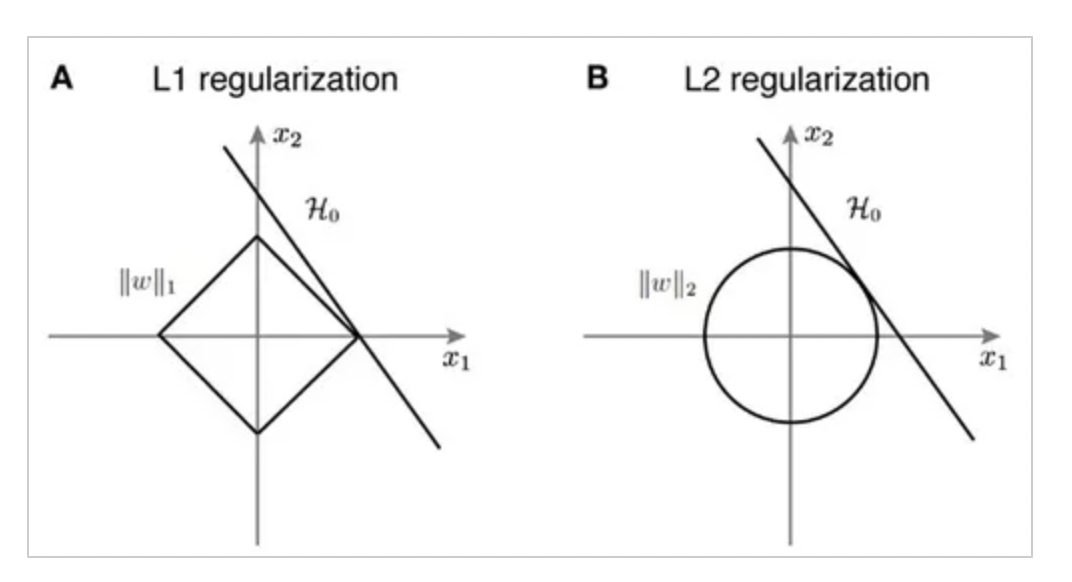
L1의 경우 Feature selection이 가능해서, Sparse Model의 경우 L1 regularization이 더 효과적이다.
하지만, 미분 불가능한 점이 있기 때문에, Gradient-base learning에서는 주의가 필요하다.
L2의 경우에는 가중치 업데이트 시에 가중치의 크기가 직접적인 영향을 끼치기 때문에 가중치 규제에 더 효과적이다.

3. Softmax

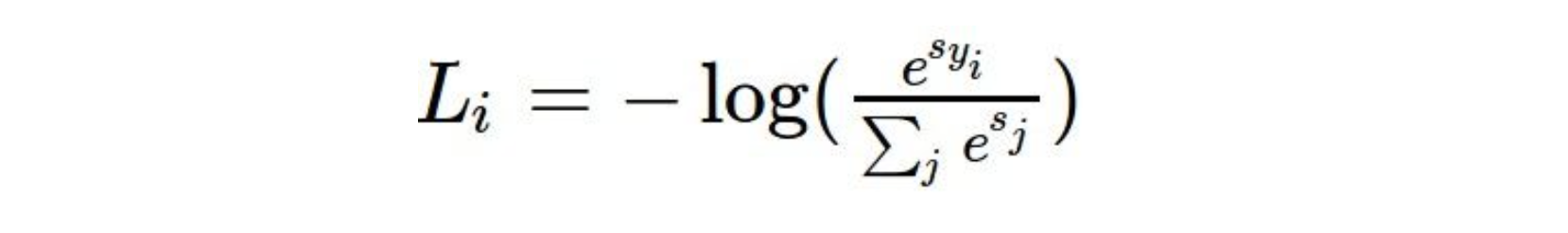Softmax function 또한, SVM Loss와 같이 loss function의 한 종류 이며, 다음과 같은 식으로 나타낼 수 있다.

4. Softmax vs SVM Loss

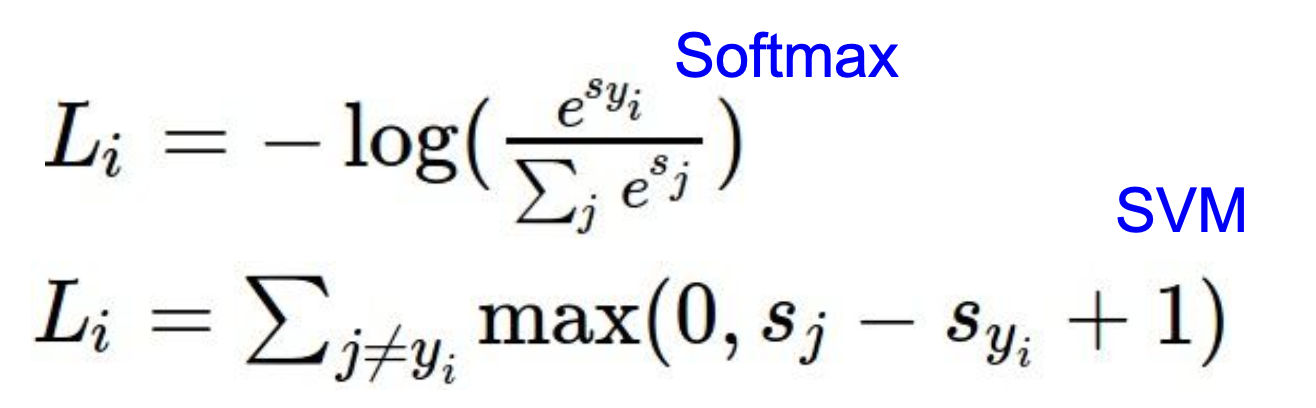
SVM의 경우 정답과 정답이 아닌 데이터와 score차이에만 집중한다. 그래서, 정답 데이터의 score를 높여도 loss가 변하지 않는 현상이 생길 수 있다.
Softmax의 경우, loss function이 확률에 로그를 씌운 형태이기 때문에, 확률을 1로 만드는 것, 즉, ${e^{s_{y_i}}}\over \sum_j e^{s_j}$ 를 1로 만드는 것에 집중한다. 그래서, 정답 score가 다른 데이터의 score보다 높은 상황에서도, class score를 계속 높이려 하므로, 성능이 계속 개선될 것이다.

5. Optimization

1) Random Search

Random하게 parameter값을 선택해, Loss function이 가장 낮은 parameter를 선택하는 것이다.
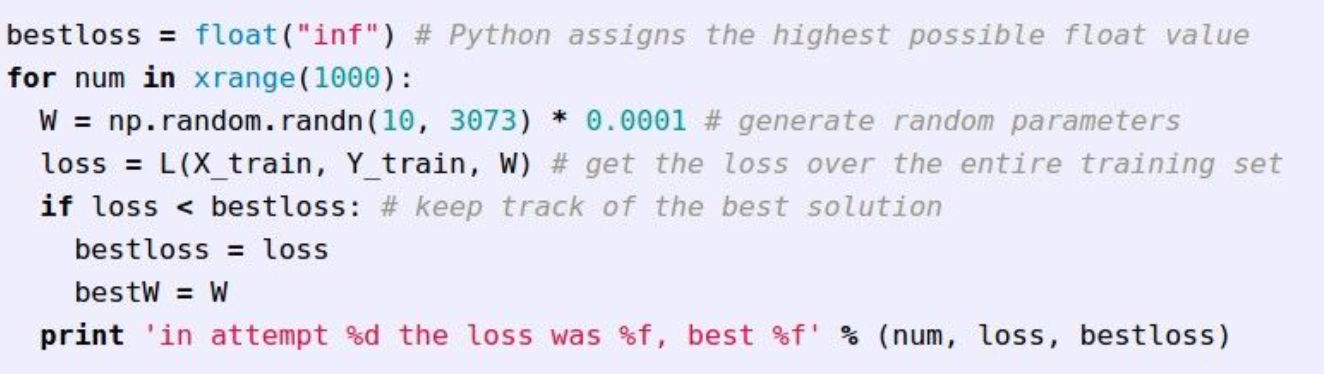코드만 봐도 학습이 상당히 느릴 것이고, 정확도도 좋지 않을 것이라고 생각될 것이다.
하지만, 여기서 배울 수 있는 점은 "반복"이다.
학습을 반복함으로써, parameter를 최선의 parameter에 가깝게 개선한다면, 최선의 parameter에 근접해질 것이다.

2) Follow the slope

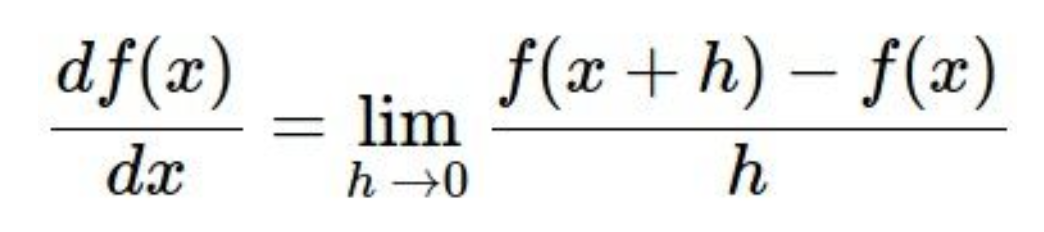loss function의 기울기가 가장 가파른 방향으로 점점 나아간다면, 최적점에 도달할 수 있을 것이다.
하지만, 여기서 기울기를 구하는 방식이 두가지로 나뉜다.

Numerical Gradient
h값을 임의로 지정해서, 각 방향마다, h만큼 나아간 지점과 원래 지점 사이의 기울기를 구해 가장 기울기가 가파른 방향으로 나아간다.
계산과정은 매우 단순하지만, h값을 임의로 지정한 작은 값이므로, 계산이 비효율적이다.
Analytic Gradient
정확한 미분식을 이용해 정확한 gradient를 구해서 최적점에 도달한다.
numerical gradient에 비해 정확하며, 계산이 빠르다.
(실제에서는, Analytic Gradient로 Gradient를 구하지만, Numerical Gradient로 정확히 구했는지 체크한다) => "Gradient Check"

3) Gradient Descent

위의 Analytic Gradient와 같이 미분을 통해, 기울기를 구해 step_size만큼 곱해서 가중치를 변화시킨다.
Loss function이 최소가 되는 방향으로 나아가야하기 때문에, gradient가 음수가 되는 쪽으로 이동해야 하므로, -를 붙인다.

SGD(Stochastic Gradient Descent)
Training data를 mini-batch로 나누어, batch마다 parameter를 갱신한다.
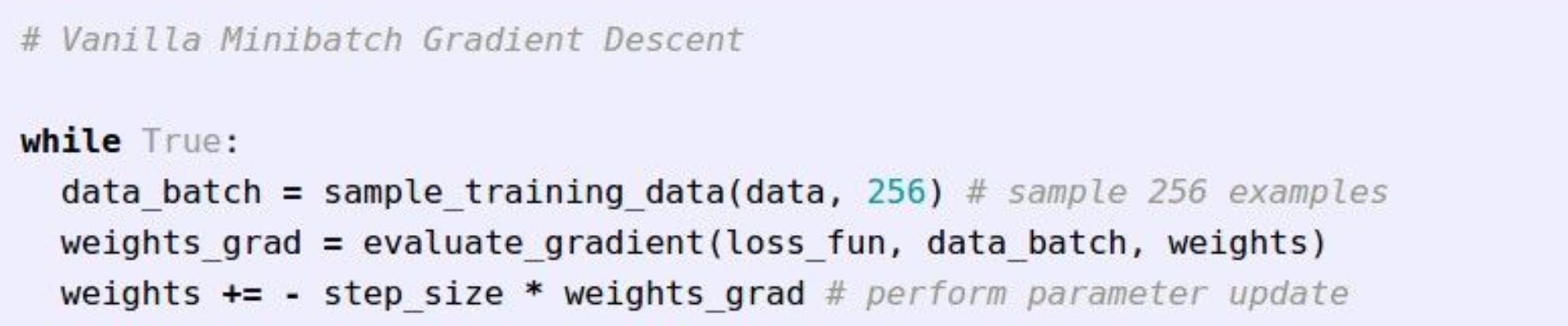이러한 이유는 Training data 전체를 거쳐서, parameter를 한번 갱신하면, 너무 비효율적이기 때문이다.