[논문 리뷰] Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks(MAML)

woonho·2023년 7월 8일

Computer Vision meta learning 논문 리뷰

Abstract

본 논문에서 제시한 모델은 MAML(Model-agnostic Meta learning)로 말 그대로 Model-agnostic한 Meta-Learning 알고리즘이다.
- Model-agnostic?
  - 모델에 상관없다는 뜻으로, 논문에서는 두가지 이유로 이 알고리즘을 model-agnostic하다고 정의하였다.
    1. Gradient descent로 학습된 어느 모델에나 적용될 수 있다.
    2. Classification, regression, reinforcementa learning과 같은 다양한 task에 대해 적용이 가능하다.
Meta-learning의 목표는 모델을 다양한 task에 대해서 학습을 시켜서 새로운 task를 접했을 때, 적은 학습 데이터만으로도 학습이 빠르게 가능한 모델을 만드는 것을 목표로 한다.
MAML은 이러한 목표를 위해 parameter들을 학습시켜서 new task에 대해 적은 gradient step 그리고, 적은 양의 학습 데이터 만으로도 좋은 generalization performance를 낼 수 있도록 하였다.
이러한 approach는 few-shot image classification benchmark에서 SOTA를 달성했고, few-shot regression에서 좋은 결과를 냈고, 또한, policy gradient reinforcement learning을 위한 fine tuning을 가속화했다.

Introduction

우리는 새로운 skill을 배우거나, 전에 보지못한 object를 인지할 때, few example만으로도 금방 학습한다. 그래서, 본 논문은 artificial agent 또한 이러한 방식이 가능하지 않을까 하는 motivation에서 시작하게 되었다. 이러한 우리의 학습 메커니즘과 비슷한 fast and flexible learning은 상당히 어려운 task이다. 왜냐하면, agent는 prior experience에 의해 학습된 모델을 new data를 통해 parameter를 업데이트 해야하지만, new data에 overfitting 되어서는 안되고, 그 뿐만 아니라 prior experience와 new data의 형태는 task에 따라서 달라진다. 그래서 이러한 greatest applicability를 위해 meta-learning mechanism은 task에 general해야하고, task의 계산 방식에 general 해야한다. 그래서 본 논문은 이러한 문제들을 해결한 general하고 model-agnostic한 meta-learning 알고리즘을 제안한다.

Key Idea

MAML method의 key idea는 model의 initial parameter를 학습시켜서 new task에 대해서 몇번의 gradient step만으로 좋은 성능을 내는 것이다. 이전 meta-learning method와 달리, MAML은 update function, learning rule을 학습하지 않기 때문에, 학습 과정에서 파라미터 개수를 늘리지 않고, 또한, 모델 구조에 제약을 받지 않는다. 이러한 특성 때문에, MAML은 fully-connected, convolutional, recurrent neural network 등에 바로 합쳐질 수 있다.

Process

모델의 파라미터를 학습하는 것은 여러 task들에 포괄적으로 적합한 internal representation을 구축하는 것으로 볼 수 있다.
이러한 internal representation이 잘 만들어졌다면, 간단한 fine-tuning 과정만으로 좋은 성능을 낼 수 있다.
그래서 본 논문은 쉽고 빠르게 fine-tune을 할 수 있고, 새로운 task에 빠르게 adaptation을 할 수 있도록 model을 optimize하고자 한다.
이러한 MAML의 학습 과정은 new task loss function의 sensitivity를 최대화 하는 것이라고 볼 수 있다.
- sensitivity가 크면, small local change 만으로, task loss가 크게 향상될 수 있다.

Contribution

meta-learning의 simple model-agnostic, task-agnostic 알고리즘을 제시했다.
- 몇 번의 gradient update 만으로 새로운 task에서 빠르게 학습가능하다.
여러 model, domain에 적용 가능한 알고리즘을 제시했다.
SOTA one-shot learning method보다 적은 parameter를 사용해서 비슷한 성능을 냈고, regression, reinforcement learning에서도 좋은 결과를 냈다.

Model-Agnostic Meta-Learning

Meta-Learning Problem Set-Up

few-shot meta-learning의 목표는 few datapoint, training iteration 만으로 새로운 task를 빠르게 학습하는 것이다. 이를 위해서 모델은 meta-learning phase에서 여러 task들을 학습해야 한다. 그래서 각 learning task는 다음과 같이 정의할 수 있다.
$\mathcal{T} = \{ \mathcal{L}(\mathbf{x}_1, \mathbf{a}_1, ..., \mathbf{x}_H, \mathbf{a}_H),q(\mathbf{x}_1), q(\mathbf{x}_{t+1} | \mathbf{x}_t,\mathbf{a}_t), H \}$
- $\mathcal{L}$ : loss function
  - loss function은 task-specific하므로, task에 따라 misclassification loss 또는 Markov decision process의 cost function을 갖는다.
- $q(\mathbf{x}_1)$ : distribution over initial observation
- $q(\mathbf{x}_{t+1} | \mathbf{x}_t, \mathbf{a}_t)$ : transition distribution
- $H$ : episode length
- $p(\mathcal{T})$ : a distribution of tasks
예를 들어, K-shot learning으로 meta-learning을 학습과정을 생각해보자.
- 먼저 Meta-training과정에서는, task $\mathcal{T}_i$ 를 $p(\mathcal{T})$ 로부터 sampling해서 task $\mathcal{T}_i$ 는 K개의 sample로 학습하고, 그로부터 도출된 loss 값 $\mathcal{L}_{\mathcal{T}_i}$ 로 feedback을 받는다.
- 그리고 새로운 sample로 test된다.
  - 이 과정에서 test error는 meta-learning의 training error가 되는 것이다.
- meata-training이 끝나면, $p(\mathcal{T})$ 로부터 새로운 task가 sampling 되고, 그 task에 대해 K개의 sampling을 이용한 학습 이후 성능으로 meta performance가 측정된다.

A Model-Agnostic Meta-Learning Algorithm

MAML의 아이디어는 가장 빨리 바뀔 수 있는 internal representation을 찾으면, task에 따라 fast adaptation이 가능할 것이라는 생각에서 motivation을 얻었다.

그래서 본 논문에서는 sensitive가 좋은 model parameter를 찾는 것을 목표로 하는데, 쉽게 말하면, parameter를 살짝만 변화시켜도 어느 task에서든 성능의 큰 개선을 만들 수 있는 model parameter를 찾는 것을 목표로 한다는 것이다.

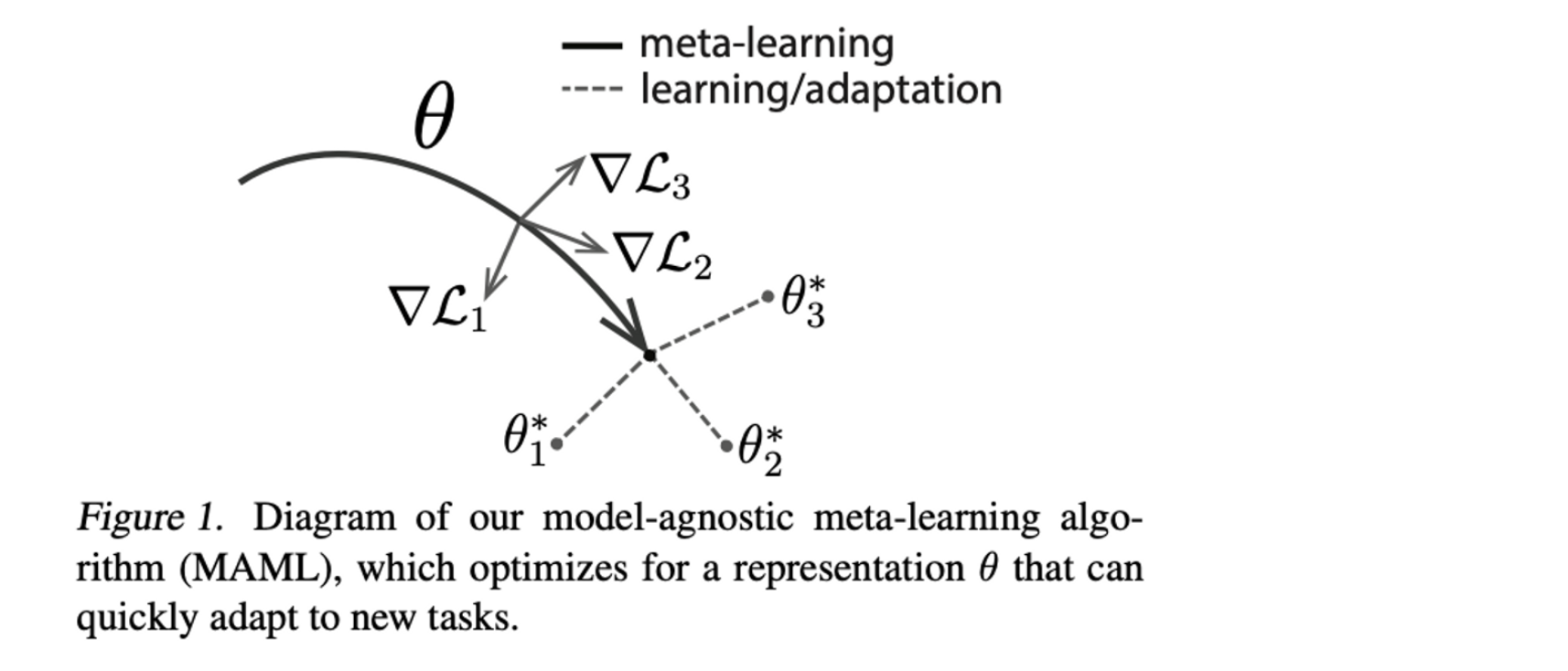
그림을 보면, sensitive가 큰 $\theta$ 를 찾아서 새로운 task에 따라 빠르게 adaptation이 가능하도록 하는 것이다.

다음은 식으로 위의 과정을 나타낸 것이다.
$\theta_i' = \theta - \alpha \nabla_\theta \mathcal{L}_{\mathcal{T}_i}(f_\theta)$
- 각 task에 대해서 task에 해당하는 Loss function으로 $\theta_i'$ 값을 update한다.
  $\min_{\theta}\sum_{\mathcal{T}_i \sim p(\mathcal{T})} \mathcal{L}_{\mathcal{T}_i}(f_{\theta_i'}) =\sum_{\mathcal{T}_i \sim p(\mathcal{T})} \mathcal{L}_{\mathcal{T}_i}(f_{\theta - \alpha \nabla_\theta \mathcal{L}_{\mathcal{T}_i(f_{\theta})}})$
- update된 $\theta_i'$ 값으로 계산된 task 별로 loss 값의 합이 최소가 되도록 $\theta$ 를 update 한다.
  $\theta \leftarrow \theta - \beta \nabla_{\theta} \sum_{\mathcal{T}_i \sim p(\mathcal{T}} \mathcal{L}_{\mathcal{T}_i}(f_{\theta_i'})$
위의 전체적인 알고리즘을 간단히 나타내면 다음과 같다.

Species of MAML

이 section에서는 위 meta-learning algorithm을 supervised learning과 reinforcement learning에 어떻게 적용했는지에 대해 설명하고 있다. domain에 따라 loss function과 data가 generate되고 model에 들어가는 방식은 다르지만 전체적인 adaptation mechanism은 동일하다.

Supervised Regression and Classification

Few-shot learning은 prior data와 새로운 task에 대한 적은 data만으로 new function을 학습시키는 것이 목표이다.
Few-shot regression과 Classification은 input과 output을 sequence형태로 받지 않고, 하나의 input, output 쌍을 받아서 학습하기 때문에 앞에서 언급한 Task의 episode length( $H)$ = 1이다. Task $\mathcal{T}_i$ 는 K개의 sample을 $q_i$ 로부터 sampling하고, task에 해당하는 loss function으로 K sample에 대해 학습한다. Regression의 경우, Loss function으로 아래와 같이 MSE를 사용하고, Classification의 경우, Cross-Entropy Loss를 사용한다.
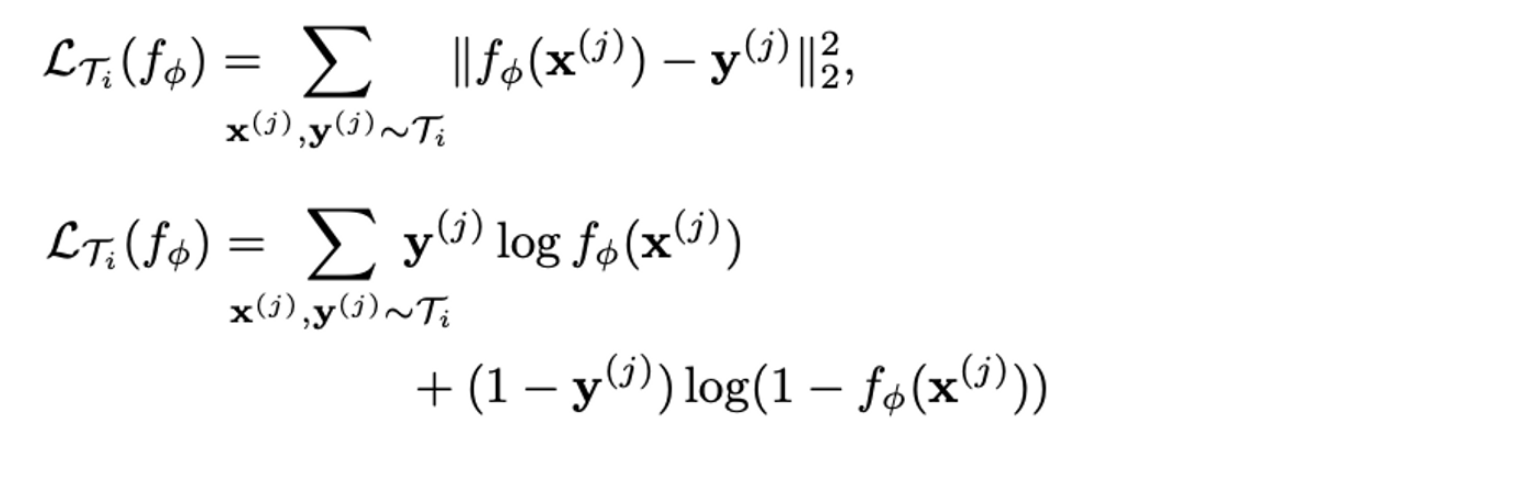
Few-shot Supervised Learning에 대한 전체적인 알고리즘은 다음과 같다.

Reinforcement Learning

Reinforcement Learning의 경우, Regression, Classification과 loss function과 data의 형태만 다르므로, loss function과 전체적인 알고리즘만 보여주고 넘어가겠다.
Loss function
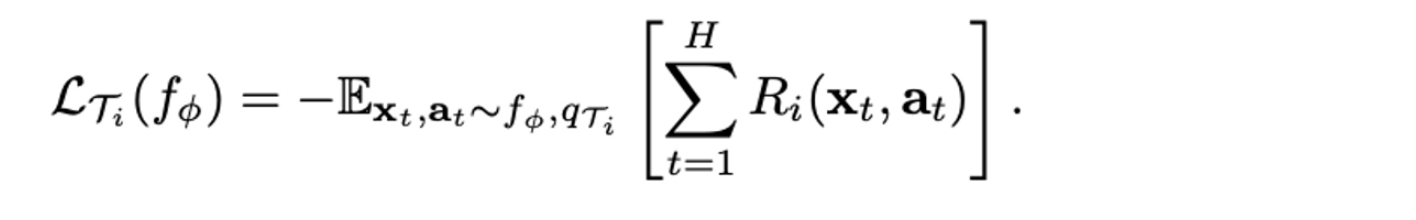
Algorithm

Experimental Evaluation

MAML은 다음의 질문에 대한 답을 찾기 위해 성능 평가가 진행되었다.
- MAML이 새로운 task를 빠르게 학습할 수 있는지?
- supervised regression, classification, reinforcement learning과 같이 여러 domain에서 사용될 수 있는지?
- MAML로 학습된 model은 additional gradient update만으로 성능이 향상될 수 있는지?

Regression

Regression에 대한 성능 평가는 sin 함수에 대해서 MAML에 의해 fine-tuning된 모델과 pretrained model과의 비교로 진행되었다.
- $p(\mathcal{T})$ : continuous, sinusoid function
  - Amplitude : [0.1, 5.0]
  - phase : [0, $\pi$ ]
  - $\mathbf{x}$ : sampled uniformly from [-5.0, 5.0]
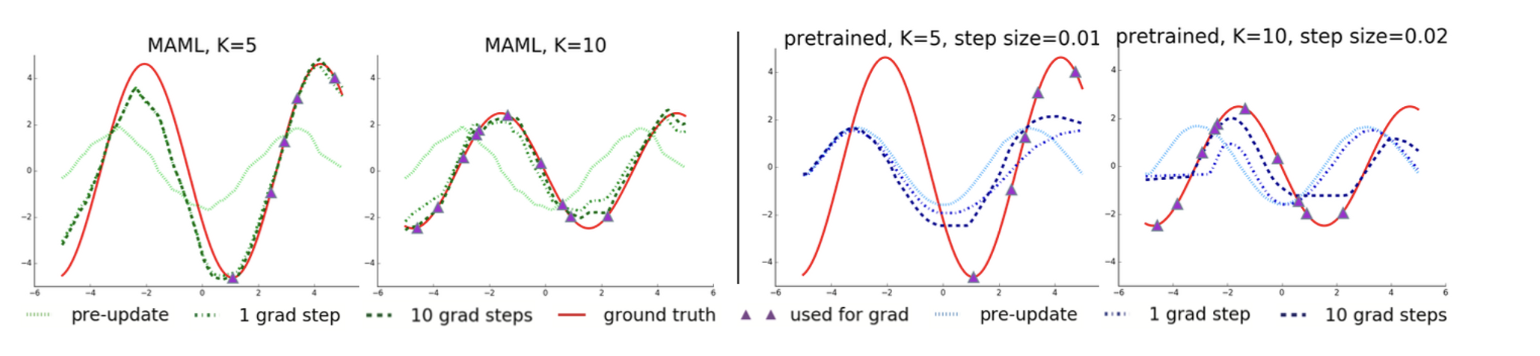
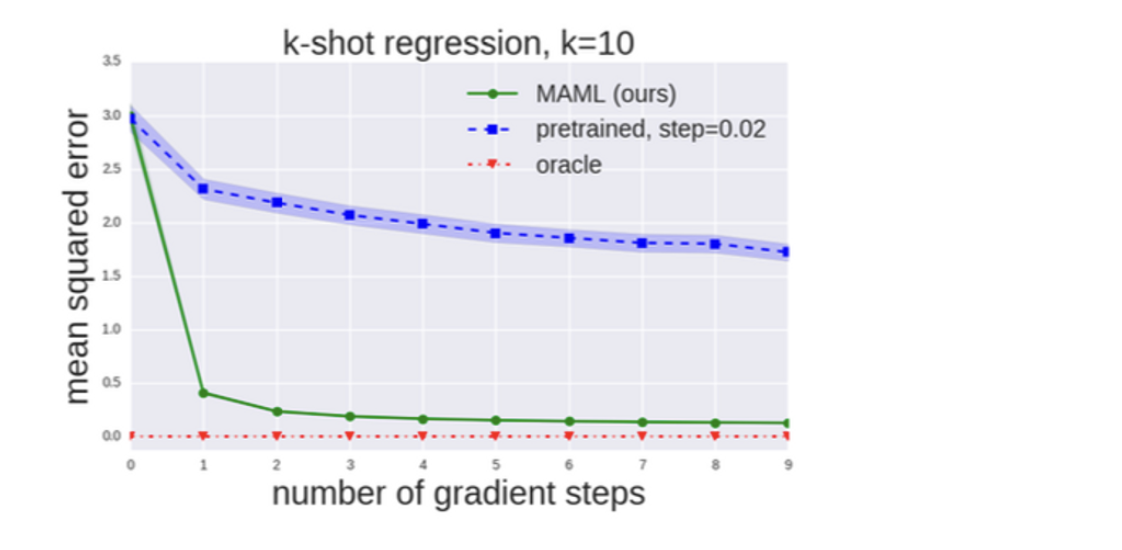
- MAML의 경우, 1 gradient step만으로도 regression의 경향성을 잘 잡아내는 반면에, pretrained model의 경우, 10 gradient steps에서도 경향성을 잘 잡아내지 못하고 있다.
MAML과 pretrained model에 대해서 MSE를 비교해봤을 때, 다음과 같다.

Classification

Classification은 기존의 few-shot learning model과의 비교로 평가가 진행되었고, dataset은 few-shot learning benchmark에서 흔히 사용되는 Omniglot과 MiniImagenet이 사용되었다.
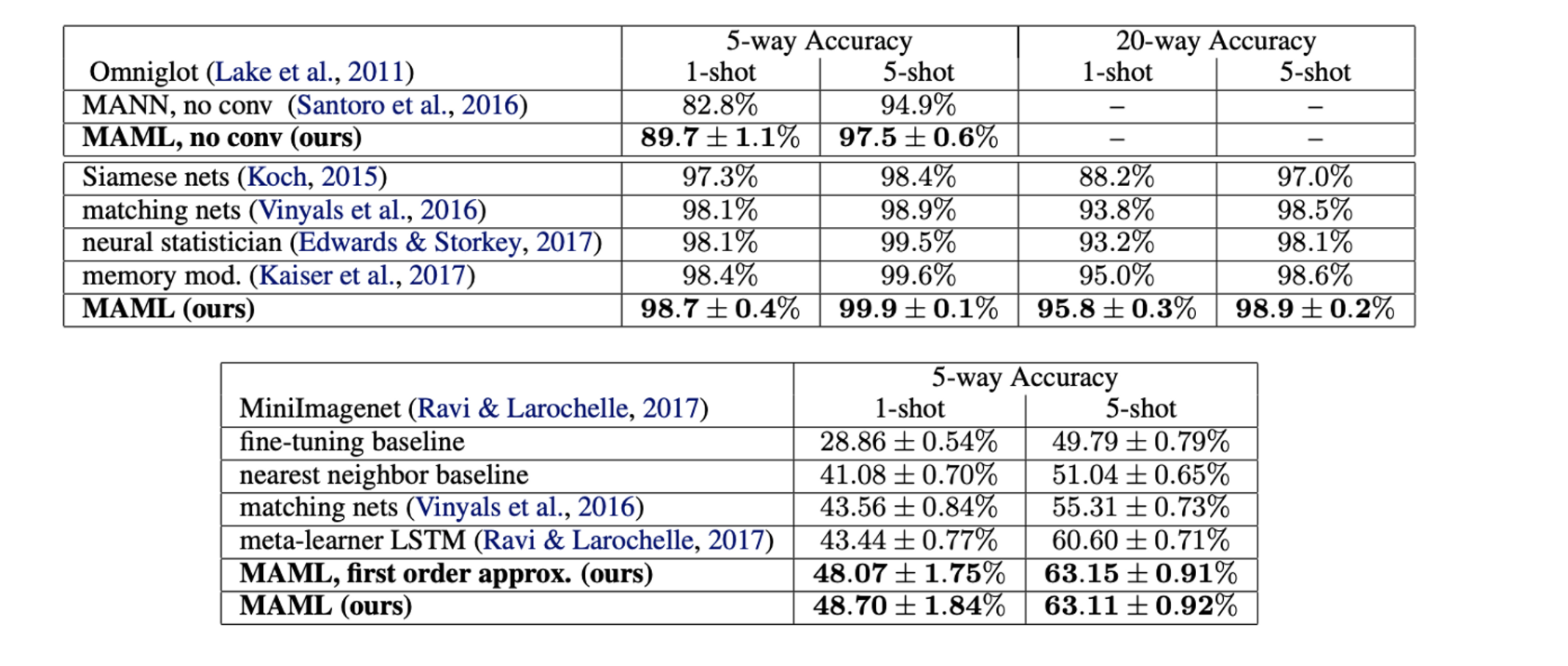
- MAML이 1-shot, 5-shot 에서 모두 기존의 Siamese network, meta-learner LSTM 등 보다 성능이 높게 나온 것을 확인할 수 있다.