이 글에서 학습하고자 하는 gradient descent 방법은 주어진 함수의 미분(gradient)를 기반으로 함수의 최소/최대값을 탐색하는 방법이다.

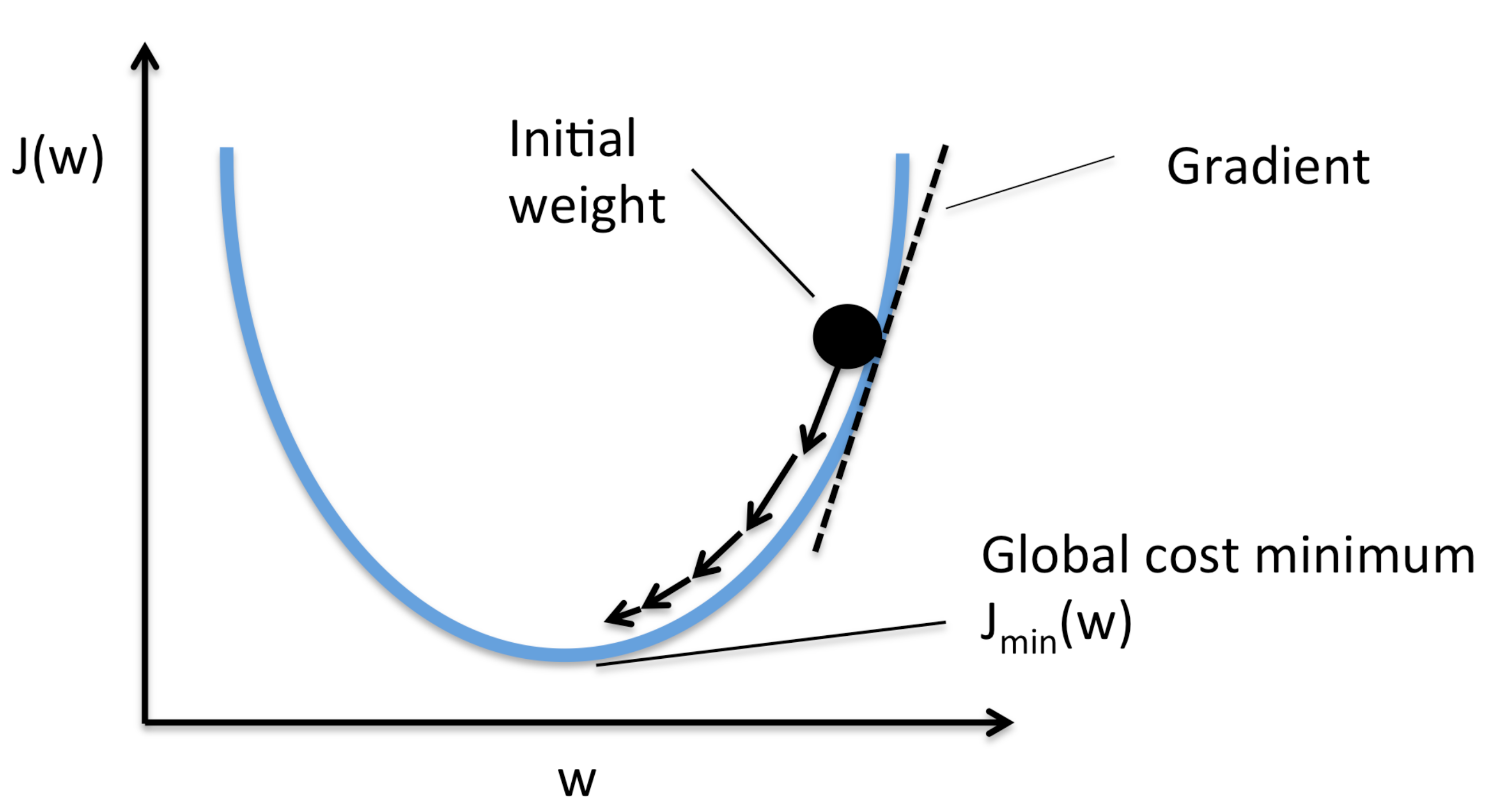
Figure 1. Gradient descent 방법의 개념

Fig 1.은 gradient descent 방법에 대한 간단한 개념을 보여준다. 함수의 미분값은 미소 부분에서의 기울기이며, 초기 위치에서 기울어진 방향을 따라 계속 이동하다보면 언젠가 기울기가 0이 되어 최소값의 위치에서 정지하게 될 것이다. 이 글에서는 이러한 gradient descent 방법을 이론적으로 살펴보는 것을 목표로 한다.

1. Gradient

SLAM 분야에서 최적화의 대상이 되는 변수는 카메라의 pose(rotation+translation)이며, 이는 회전각, 이동방향 등 여러 변수를 포함되어 있다. 따라서 카메라의 pose에 대해서 기술된 cost 함수 등은 여러개의 변수를 다루는 다변수 함수가 된다.

다변수 함수를 분석하기 위하여 함수의 미분을 구하게 되는데, 가장 쉽게 떠올릴 수 있는 방법은 일변수 함수와 비슷한 편미분(partial derivative)이다. 편미분은 다변수 함수에 속해 있는 하나의 변수에 대해서만 미분을 수행하며, 해당 변수에 대한 특성을 알 수 있다.

예를 들어 $f(x,y)$와 같이 두 개의 변수를 입력으로 받는 함수가 있다고 할 때, $g_{y=a}(x)=f(x, a)$를 $x$에 대해 미분함으로써 $y=a$에서 $x$의 변화에 따른 특성을 알 수 있다. 미분의 정의를 사용하면 다음과 같이 편미분을 계산할 수 있다.

이러한 편미분은 $f_y(x, a), \partial f /\partial x$등과 같이 표현하기도 한다($y=a$일 때, $x$에 대한 편미분).

전미분(total derivative)는 편미분과 달리 모든 방향에 대한 미분을 수행한다. 만약 $f:\mathcal{R}^n \rightarrow \mathcal{R}$이라고 할 때, 다음과 같이 $\mathbf{x}_0$에서의 전미분을 정의할 수 있다.

즉, 모든 방향으로 편미분을 하고 그 결과를 합한 것이라고 볼 수 있다. 그렇다면 만약 $f:\mathcal{R}^n \rightarrow \mathcal{R}^m$이면 어떻게 될까? 이 경우에는 $f$를 행렬처럼 생각할 수 있다. 어떤 $m \times n$ 행렬에 $n$차원 벡터를 곱할 경우 결과는 $m$차원 행렬이므로 $f:\mathcal{R}^n \rightarrow \mathcal{R}^m$이라고 할 수 있다. 이때, $m \times n$ 행렬의 n번째 행과 입력 벡터가 곱해져 n번째 값을 생성하는데, 이를 함수 $f$안에 여러 개의 함수($f_1, \cdots, f_m$)이 들어있다고 생각할 수 있다. 이러한 함수에 전미분을 수행하면 다음과 같이 행렬의 형태로 나타낼 수 있다.

이때, 미분의 결과로 생성된 행렬 $\mathbf{J}(\mathbf{x}_0)=f'(\mathbf{x}_0)$를 $\mathbf{x}_0$에서 함수 $f$의 Jacobian이라고 하며, 만약 $f:\mathcal{R}^n \rightarrow \mathcal{R}$일 때라면 $\nabla f = (\partial f(\mathbf{x}_0)/\partial x_1 + \cdots + \partial f(\mathbf{x}_0)/\partial x_n)$로 쓰기도 한다.

$\nabla f$의 형태를 보면 다음과 같이 $\nabla$ 마치 어떤 연산자로 작용하는 형태이다.

실제 벡터곱은 아니지만 위와 같이 $\nabla$을 del 연산자로써 사용하면 여러가지로 편리할 수 있으며, 실제로 대부분의 부분에서 벡터 연산과 같이 작동한다.

$\alpha:\mathcal{R}\rightarrow \mathcal{R}^n, \alpha(t) = \mathbf{p}+t\mathbf{q}$라면, $F(t)=f(\alpha(t))=f(\mathbf{p}+t\mathbf{q})$일 때, n차 미분은 $F^{(n)}(t)=(\mathbf{q}\cdot \nabla)^n f(\mathbf{p}+t\mathbf{q})$로 주어진다.

$\alpha(t) = \mathbf{p}+t\mathbf{q}$와 같이 매개변수를 도입하며 고계도 미분을 정의하는 이유는 이후에 소개될 여러 최적화 방법에서 "초기값+방향*이동거리"의 형태로 값을 업데이트해가며 최적의 값을 탐색하기 때문이다.

특히 위의 방법을 통해 구해진 2차 미분의 경우 Hessian 행렬이라고 부르며, 3차 이상의 term 부터는 근사를 통해 사용되지 않는 경우가 많지만 Hessian 행렬까지는 많이 사용된다.

위의 식의 작동을 살펴보기 위하여 $f:\mathcal{R}^3 \rightarrow \mathcal{R}$의 예시를 살펴보자. 1차 미분은 다음과 같으며, 아래에서 구한 식과 위의 식이 일치함을 알 수 있다.

$F'(t)=\nabla f(\alpha(t)) \cdot \mathbf{q}=q_1f_x(\alpha(t))+q_2f_y(\alpha(t))+q_3f_z(\alpha(t))$으로 풀어쓰고, 비슷한 방식으로 2차 미분을 구해보면 다음과 같다.

여기서 $f_{xy}$ 등은 $f$를 $x$에 대해 편미분한 결과에서 다시 $y$로 편미분한 것이다. 이때, 같은 지점에서 미분을 수행했다면 $f_{xy}=f_{yx}$이다. 이를 이용하여 위의 식을 정리하면 다음과 같다.

n차 미분에도 비슷한 방법으로 유도가 가능하며, 또한 (*)식에서 $F^{(2)}(t)=\mathbf{q}\cdot \mathbf{H}f(\mathbf{p}+\mathbf{q}t)\cdot \mathbf{q}^T$형태로 쓸 수 있으며, $\mathbf{H}$를 Hessian 행렬이라고 하며, 다음과 같다.

이때, $\alpha(t) = \mathbf{p}+t\mathbf{q}$와 같이 매개변수를 도입했기 때문에 2차 미분이 $F^{(2)}(t)=\mathbf{q}\cdot \mathbf{H}f(\mathbf{p}+\mathbf{q}t)\cdot \mathbf{q}^T$와 같은 형태로 나왔지만 일반적으로 $f''(\mathbf{x})$를 구할 경우 $\mathbf{H}f(\mathbf{x})=\frac{\partial^2 f(\mathbf{x})}{\partial x_i \partial x_j}$로 쓸 수 있다.

이를 이용하면 $f:\mathcal{R}^n \rightarrow \mathcal{R}$에 대한 Taylor 전개를 다음과 같이 쓸 수 있다. 여기서 $\mathbf{p_0}=\mathbf{p}+t_0(\mathbf{q}-\mathbf{p})$, 즉, $\mathbf{p_0}$는 $\mathbf{q}, \mathbf{p}$사이의 어떤 값이다. Taylor 전개는 일정 구간 내에서 함수가 n번 미분이 가능할 때 다음과 같이 n계도함수를 사용하여 표현할 수 있음을 보여주며, 그 외에도 주어진 함수가 미소영역에서 선형성을 갖고 있을 경우 고차항을 무시하여 선형식으로 근사하기 위해서도 사용된다.

이제 이와 관련된 몇가지 성질을 살펴보자.

• $\nabla f(\mathbf{x}_0)=0$을 만족하는 점 $\mathbf{x}_0$를 임계점(critical point)라고 함
• $h(\mathbf{x})=g(f(\mathbf{x}))$일 때, $\nabla h(\mathbf{x})=g'(f(\mathbf{x}))f'(\mathbf{x})=g'(f(\mathbf{x}))\nabla f(\mathbf{x})$이므로 $g'(f(\mathbf{x_0})) \ne 0$이면 $\nabla f(\mathbf{x}_0) = 0 \leftrightarrow\nabla h(\mathbf{x}_0)=0$
• $\mathbf{H}f(x_0)$가 positive definite이면, $x_0$는 국소 최소
• $\mathbf{H}f(x_0)$가 negative definite이면, $x_0$는 국소 최대
• $\mathbf{H}f(x)$가 $x_0$에서 부호가 바뀌면 saddle point

마지막으로 gradient 벡터의 방향은 최적화 방법에서 많은 아이디어를 주는데 이에 대한 내용을 살펴보자.

$\nabla f$는 $f$를 모든 방향에 대해서 미분한 것이고, 편미분은 하나의 값에 대해서 미분한 것이다. 그렇다면 특정 방향으로의 변화량(미분)은 어떻게 구할 수 있을까?

미소 영역에 대해서 $f(\mathbf{x})=f(\mathbf{a})+f_{x_1}(\mathbf{x_1}-\mathbf{a_1})+\cdots+f_{x_n}(\mathbf{x_n}-\mathbf{a_n})$으로 근사할 수 있고, 이를 이용하여 방향 미분을 미분의 정의를 이용해 구해보면 다음과 같다($\mathbf{u}$방향으로의 미분).

따라서 $\mathbf{u}$방향으로의 미분은 $\nabla f(\mathbf{a})\cdot\mathbf{u}$로 주어지며, $\nabla f(\mathbf{a})\cdot\mathbf{u}$가 최대가 되는 경우는 $\nabla f(\mathbf{a})$와 $\mathbf{u}$가 같은 방향일 때 이므로, $\nabla f(\mathbf{a})$의 방향은 주어진 함수가 가장 빠르게 변화하는 방향이다.

이제까지 함수 $f$에 대한 Hessian 행렬이라는 의미로 $\mathbf{H}f(x)$와 같이 작성하였지만 아래 내용부터는 간소화하여 $\mathbf{H}(x)$로 작성한다.

2. Newton's Method

기본적인 gradient descent 기반 방법의 아이디어는 위에서 보았듯이 함수값이 작이지는 방향(그레이언트)를 따라서 입력값을 업데이트 해나가는 과정을 반복적으로 수행하여 최소값(또는 최대값)을 찾는 것이다. 그 과정은 다음과 같이 쓸 수 있다.

• Step1: 초기값 설정 ($\mathbf{x}_0$)
• Step2: 함수의 하강 방향 계산 ($\mathbf{b}$)
• Step3: 다음 계산 위치 업데이트 ($\mathbf{x}_1 \leftarrow \mathbf{x}_0 + \alpha \mathbf{b}$)
• Step4: step 2~3을 반복

여기서 살펴볼 Newton 방법 또한 기본적으로 gradient descent 방법을 기반으로 하고 있으며, 함수의 하강 방향 및 그 이동 크기($\alpha$)를 결정하는 방법을 제시한다.

일반적으로 함수 $f$에 Taylor 급수를 적용하면 다음과 같다.

위의 식에서 $\mathbf{h}$가 충분히 작다면 $|\mathbf{h}|^3$은 생략하여 근사할 수 있다. 우리의 목표는 업데이트 방향($\mathbf{h}$)을 구하는 것으로 해당 방향으로 업데이트($\mathbf{x}+\mathbf{h}$)했을 때, 함수값이 감소하여야 한다. 이를 구하기 위하여 위의 식을 다음과 같이 고정된 위치 $\mathbf{x}$에서의 $\mathbf{h}$에 대한 식으로 쓰면 다음과 같다.

위의 식을 최소로 하는 $\mathbf{h}$를 찾아야 하며, critical point에서는 미분값이 0이 되어야 함을 이용하기 위해 위의 식을 미분하면 다음과 같다.

따라서 업데이트 방향은 $\mathbf{h} = -\mathbf{H}^{-1}(\mathbf{x})\nabla f(\mathbf{x})$로 주어지고, 만약 2계도함수 $\mathbf{H}(\mathbf{x})$가 positive definite라면 해당 업데이트 방향은 함수값을 최소로하는 방향이다(위의 기본 알고리즘에 따라 방향은 그레이디언트 $\nabla f(\mathbf{x})$, step size가 $-\mathbf{H}^{-1}$로 주어진다고 볼 수도 있음). 위와 같은 최적화 방법을 Newton's method라고 한다.

일반적으로 SLAM 등의 분야에서는 다음과 같은 최소제곱문제를 해결하는 것을 목표로 한다. 여기서 $\mathbf{f}(\mathbf{x})=(f_1(\mathbf{x})), \cdots, f_n(\mathbf{x})))$이며, $\mathbf{f}: \mathcal{R}^n \rightarrow \mathcal{R}^m$인 비선형 함수이다.

여기서 우리는 비선형 함수도 미소 영역에서는 선형적인 특성을 갖는 성질을 활용한다. 이 성질과 Taylor 전개를 사용하여 위의 비선형함수 $\mathbf{f}$를 1차 근사하면 다음과 같다.

이를 이용하여 위의 목표식 $F$를 근사하면 다음과 같다.

위의 식을 $\mathbf{h}$에 대해서 미분하여 $L(\mathbf{h})$를 최소로 하는 $\mathbf{h}$, 즉 하강방향을 찾을 수 있다.

따라서 하강방향은 $\mathbf{h}=-(\mathbf{J}(\mathbf{x})^T\mathbf{J}(\mathbf{x}))^{-1}\mathbf{J}(\mathbf{x})^T\mathbf{f}(\mathbf{x})$로 주어지며, 위의 식에서 Hessian이 $\mathbf{J}(\mathbf{x})^T\mathbf{J}(\mathbf{x})$와 같이 Jacobian 행렬로 근사되었음을 알 수 있다.

만약 $\mathbf{J}(\mathbf{x}))$의 열벡터가 일차 독립이면, $L''(\mathbf{h}) = \mathbf{J}(\mathbf{x})^T\mathbf{J}(\mathbf{x})$은 positive definite이며(참고), 따라서 Hessian의 역행렬은 존재하고 위의 업데이트 방향이 최소값을 찾는 방향임을 의미한다. 이러한 최적화 방법을 Gauss-Newton's method라고 한다.

하지만 이러한 Newton 방법은 문제점이 있는데, 함수 전체에서 $\mathbf{H}(\mathbf{x})$가 positive definite임이 보장되지 않는다는 점이다. 초기값이 최소점 근처라면 그 지점에서의 $\mathbf{H}(\mathbf{x})$는 positive definite이겠지만, 만약 초기값을 잘못 설정하면 이러한 가정이 깨져 알고리즘이 잘 작동하지 않을 수 있다. 또한 Hessian 행렬을 계산함에 있어 수치적으로 역행렬이 존재하지 않을 수 있으며, 비가역적인 형태에 가까워질 수록 계산상의 불안정성이 커질 수 있다.

따라서 아래에서 이러한 문제점을 해결할 수 있는 Levenberg-Marquardt방법과 Quasi-Newton방법을 살펴본다.

4. Levenberg-Marquardt Method

Levenberg-Marquardt방법에서는 현재 위치가 최소값에서 멀다면 그레디언트 방향으로 일정 상수 길이만큼 이동하는 일반 gradient descent 방법을 사용하고, 적당히 가깝다면 Hessian 행렬을 이용한 Newton 방법을 사용한다. Levenberg-Marquardt방법에서는 다음과 같이 업데이트 방향을 수정한다.

위와 같은 식에서 얻을 수 있는 효과는 다음과 같다.

먼저, $(\mathbf{J}(\mathbf{x})^T\mathbf{J}(\mathbf{x})+\mu\mathbf{I})$이 항상 positive definition이 된다. 이를 통해 수치적인 안정성을 얻을 수 있다.

다음으로 큰 $\mu$에 대해서는 $\mathbf{J}(\mathbf{x})^T$가 상대적으로 작아져 무시할 수 있게 되고, 업데이트 방향이 $\mathbf{h}\approx -\mathbf{J}(\mathbf{x})^T\mathbf{f}(\mathbf{x})/\mu$로 주어지는 일반 gradient descent 방법이 되며, 해에서 멀리 떨어진 경우에 좋은 수렴성을 갖도록 한다.

마지막으로 매우 작은 $\mu$에 대해서는 Gauss-Newton's method와 일치하여 해의 근처에서 좋은 수렴성을 갖도록 한다.

여기서 사용된 $\mu$는 매 단계마다 업데이트 되는 값이며 다음과 같은 식을 사용한다.

위의 식에서 $\mathbf{J}(\mathbf{x})^T\mathbf{J}(\mathbf{x})$는 적어도 positive semidefinite이다. 그렇다면 $F$에 대한 근사식인 $L$은 최소값을 갖는 오목한 형태와 비슷할 것이며, $\rho$는 그 근사값과 실제 값 사이의 유사도를 측정한다. 따라서 그 유사도가 높다면 업데이트가 수행되는 위치에서 실제 함수 $F$ 또한 오목한 형태에 가깝다는 말이고, 그 만큼 해에 근접했다고 볼 수 있어 $\mu$를 줄이게 되며, 그 반대의 상황이라면 해에서 멀리 떨어져있다는 의미이므로 $\mu$를 크게 한다.

$\mu$의 업데이트는 $\rho$가 0.75 초과이면 $\mu \leftarrow\mu/3$, 0.25 미만이면 $\mu \leftarrow\mu\cdot3$과 같이 하거나 0 초과이면 $\mu \leftarrow \mu\cdot \max{(1/3, 1-(2\rho-1)^3)}$, 그렇지 않으면 $\mu \leftarrow\mu\cdot3$과 같이 하는 등 여러 방법이 있을 수 있다.

다만 이러한 Levenberg-Marquardt방법에서는 역행렬을 계산해야하기 때문에 계산 복잡도가 높아질 수 있다.

3. Quasi Newton’s Method

Quasi Newton’s Method에서는 앞에서 사용했던 Hessian 행렬을 쉽게 미분 가능한 positive definite 행렬로 근사하는 방법을 제시하며, 이를 통해 업데이트 계산을 쉽게 수행할 수 있다.

이를 위하여 다음과 같이 $\nabla f(\mathbf{x})$를 $\mathbf{x}_n$에서 근사해보자

여기서 $\mathbf{y}=f(\mathbf{x}_n)-\nabla f(\mathbf{x})$, $\mathbf{h}=\mathbf{x}_n-\mathbf{x}$이며, $\mathbf{B}_{new}$를 이용하여 Hessian 행렬을 근사하였다.

이전 step에서 사용한 $\mathbf{B}$를 알고 있을 때, $\mathbf{B}_{new} \leftarrow \mathbf{B} + \mathbf{W}$로 업데이트를 하는 것이 목표이며, 이 식을 위에 대입하면 다음과 같다.

따라서 이를 만족하는 $\mathbf{W}$를 찾으면 Hessian 근사 행렬인 $\mathbf{B}$를 업데이트 할 수 있으며, 여러 업데이트 방식이 제안되었지만, 다음의 식을 사용한 BFGS방법이 대표적이다.

해당 방법을 이용하면 Hessian 행렬을 쉽게 미분 가능한 positive definite 행렬로 근사할 수 있고, 근사 행렬 $\mathbf{B}$를 앞에서 학습한 Newton's method 등에서 사용된 Hessian을 대체하여 사용한다.

5. Lagrange Multiplier Method(제약조건이 있는 경우)

• 참고: https://xoft.tistory.com/82, "최적화이론(임장환 지음)"