다차원 배열의 연산

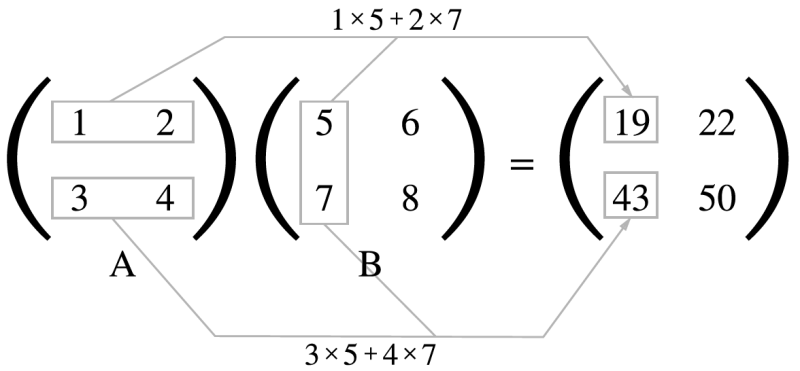
행렬의 내적

2차원 배열인 행렬의 내적을 구하는 방법

행렬의 내적은

• 왼쪽 행렬의 행( 가로 )과 오른쪽 행렬의 열( 세로 )을 원소 별로 곱하고 그 값들을 더한다.
• 계산의 결과가 새로운 다차원 배열의 원소가 된다.
• 행렬은 보통 대문자로 표시하는 것이 관례이다.

import numpy as np

A = np.array([[1, 2],
	      [3, 4])
             
B = np.array([5, 6],
	     [7, 8])

print('행렬 A의 shape : {} ' .format(A.shape))
print('행렬 B의 shape : {} ' .format(B.shape))

~~>
행렬 A의 shape : (2, 2)
행렬 B의 shape : (2, 2)

행렬의 내적은 연산자 @를 사용하거나 np.dot 함수를 사용하면 구할 수 있다.

print('A와 B의 내적 : \n{}' .format(np.dot(A, B))
~~>
A와 B의 내적 :
[[19 22]
 [43 50]]

print('A와 B의 내적 : \n{}' .format(A @ B))
~~>
A와 B의 내적 :
[[19 22]
 [43 50]]

✨행렬의 내적은 교환법칙이 성립되지 않는다.

print(A @ B)
~~>
[[19 22]
 [43 50]]

print(B @ A)
~~>
[[23 34]
 [31 46]]

행과 열의 개수가 다른 상태에서의 행렬 내적

💡 규칙 : 첫 번째 행렬의 1번째 차원의 원소의 수( 열의 수 )와, 두 번째 행렬의 0번째 차원의 원소수( 행의 수 )가 일치하면 행렬의 내적을 구할 수 있다.

A = np.array([[1, 2, 3],
	      [4, 5, 6]]) # shape : (2, 3)
B = np.array([[1, 2],
	      [3, 4],
              [5, 6]])
print(A @ B)

~~>
[[22 28]
 [49 64]]
 
print(B @ A)

~~>
[[9 12 15]
 [19 26 33]
 [29 40 51]]

C = np.array([[1, 2],
	      [3, 4]])

👉 A @ C 연산은 불가능 : (2, 3) @ (2, 2)
👉 C @ A 연산은 가능 : (2, 2) @ (2, 2)

print(C @ A)

~~>
[[9 12 15]
 [19 26 33]]

차원 수가 달라도 계산은 가능

A = np.array([[1, 2],
	      [3, 4],
              [5, 6]])

B = np.array([7, 8]) # 행 벡터의 모형을 하고 있지만 numpy 에서는 열 벡터로 표현이 된다.

A.shape, B.shape

~~>
((3, 2), (2, ))

print(A @ B)

~~>
[23 53 83]

👉 B @ A 연산은 할 수 없다.