행렬과 신경망

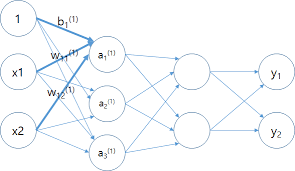
신경망의 입력값과 가중치

• 신경망에 입력되는 값은 여러 개이다.
• 입력값에 해당하는 가중치도 여러 개이다.

import numpy as np

X = np.array([1, 2])
print('입력값 X의 shape : {}' .format(X.shape))

~~>
입력값 X의 shape : (2, )

W = np.array([[1, 2, 3], # x1에 곱해질 가중치
	      [4, 5, 6]) # x2에 곱해질 가중치
print('가중치 W의 shape : {}' .format(W.shape))

~~>
가중치 W의 shape : (2, 3)

👉 첫번째 뉴런에는 1, 4
👉 두번째 뉴런에는 2, 5
👉 세번째 뉴런에는 3, 5

X @ W  # W @ X 는 안된다.

~~>
array([ 9, 12, 15])

W.T @ X

~~>
array([ 9, 12, 15])

신경망을 행렬로 표기하기

• 1층을 구성하는 표기
  • 1층의 1번째 뉴런만 표기 :

    $z_1^{(1)} = w_{11}^{(1)}x_1 + w_{12}^{(1)}x_2+b_1^{(1)}$
    
    

  • 1층 전체를 나타내기 :

    B의 원소 수는 뉴런의 개수와 같다.
    
    $Z^{(1)} = XW^{(1)} + B^{(1)}$
    
    

    • $X = (x_1, x_2)$
      
      
    • $W^{(1)} = \begin{pmatrix}w_{11}^{(1)} & w_{21}^{(1)} & w_{31}^{(1)} \\ w_{12}^{(1)} & w_{22}^{(1)} & w_{32}^{(1)} \end{pmatrix}$
      
      
    • $B^{(1)} = \begin{pmatrix}b_1^{(1)}&b_2^{(1)}&b_3^{(1)}\end{pmatrix}$
      
      
    • $Z^{(1)} = \begin{pmatrix}z_1^{(1)}&z_2^{(1)}&z_3^{(1)}\end{pmatrix}$
      
      

X = np.array([1.0, 0.5])
W1 = np.array([0.1, 0.3, 0.5],
	      [0.2, 0.4, 0.6])
B1 = np.array([0.1, 0.2, 0.3])

print('입력값 X의 shape : {}' .format(X.shape))
print('첫 번째 층의 가중치 W1의 shape : {}' .format(W1.shape))
print('첫 번째 층의 편향 B1의 shape : {}' .format(B1.shape))

~~>
입력값 X의 shape : (2, )
첫 번째 층의 가중치 W1의 shape : (2, 3)
첫 번째 층의 편향 B1의 shape : (3, )

Z1 = np.dot(X, W1) + B1

print('1층 결과물 Z1의 shape : {}' .format(Z1.shape))
print('1층 결과물 Z1 행렬 : {}' .format(Z1))

~~>
1층 결과물 Z1의 shape : (3, )
1층 결과물 Z1 행렬 : [0.3 0.7 1.1]

활성화 함수 적용하기

뉴런마다 활성화 함수를 한꺼번에 적용

sigmoid

def sigmoid(x):
	return 1 / (1 + np.exp(-x))
    
A1 = sigmoid(Z1)

print('원래 Z1 : {}' .format(Z1))
print('활성화 함수( 시그모이드 ) 적용 후 A1 : {}' .format(A1))

~~>
원래 Z1 : [0.3 0.7 1.1]
활성화 함수( 시그모이드 ) 적용 후 A1 : [0.57444252 0.66818777 0.75026011]

실습

💡 1층에서 2층으로 넘어가는 과정까지 추가해서 전체적인 신경망 구성

2층 은닉층

W2 = np.array([0.1, 0.4],
	      [0.2, 0.5],
              [0.3, 0.6]])
B2 = np.array([0.1, 0.2])

print('두 번째 층의 가중치 W2의 shape : {}' .format(W2.shape))
print('두 번째 층의 편향 B2의 shape : {}', format(B2.shape))

~~>
두 번째 층의 가중치 W2의 shape : (3, 2)
두 번째 층의 편향 B2의 shape : (2, )

Z2 = np.dot(A1, W2) + B2
A2 = sigmoid(Z2)

print('원래 Z2 : {}' .format(Z2))
print('활성화 함수( 시그모이드 ) 적용 후 A2 : {}' .format(A2))

~~>
원래 Z2 : [0.51615984 1.21402696]
활성화 함수( 시그모이드 ) 적용 후 A2 : [0.62624937 0.7710107 ]

3번 은닉층

W3 = np.array([[0.1, 0.3],
	       [0.2, 0.4]])
B3 = np.array([0.1, 0.2])

print('세 번째 층의 가중치 W3의 shape : {}' .format(W3.shape))
print('세 번째 층의 편향 B3의 shape : {}' .format(B3.shape))

~~>
세 번째 층의 가중치 W3의 shape : (2, 2)
세 번째 층의 편향 B3의 shape : (2, )

항등함수( identitly function ) 활용

마지막 층을 위한 활성화 함수로 항등함수를 사용

def identity_function(x):
	return x

Z3 = np.dot(Z2, W3) + B3
A3 = identity_function(Z3)

print('원래 Z3 : {}' .format(Z3))
print('활성화 함수( 시그모이드 ) 적용 후 A3 : {}' .format(A3))

~~>
원래 Z3 : [0.39442138 0.84045873]
활성화 함수( 시그모이드 ) 적용 후 A3 : [0.39442138 0.84045873]

정리

• 신경망의 레이어는 뉴런들을 가지고 있다.
• 뉴런들을 가지고 있다는 이야기는 각 뉴런 마다의 가중치와 편향을 가지고 있다.
• 따라서 처음 신경망을 구성 할 때는 랜덤으로 초기화 되어있는 가중치와 편향을 저장하고 있어야한다. 👉 신경망의 구조를 미리 알고 있어야 한다.

1층 계산

Z1 = X @ W1 + B1
A1 = sigmoid(Z1)

2층 계산

Z2 = A1 @ W2 + B2
A2 = sigmoid(Z2)

3층 계산

Z3 = A2 @ W3 + B3
Y = identity_function

Y
~~>
array([0.31682708, 0.69627909])

def init_network():
    network = {}

    # 1층에 대한 정보
    network['W1'] = np.array([[0.1, 0.3, 0.5],
                              [0.2, 0.4, 0.6]])
    network['b1'] = np.array([0.1, 0.2, 0.3])

    # 2층에 대한 정보
    network['W2'] = np.array([[0.1, 0.4], 
                              [0.2, 0.5], 
                              [0.3, 0.6]])
    network['b2'] = np.array([0.1, 0.2])

    # 3층에 대한 정보
    network['W3'] = np.array([[0.1, 0.3],
                              [0.2, 0.4]])
    network['b3'] = np.array([0.1, 0.2])
    
    return network

# 순전파 구현
def forward(network, x):
  # 가중치, 편향 꺼내기
  W1, W2, W3 = network['W1'], network['W2'], network['W3']
  b1, b2, b3 = network['b1'], network['b2'], network['b3']

  # 1층 계산
  Z1 = np.dot(x, W1) + b1
  A1 = sigmoid(Z1)

  # 2층 계산
  Z2 = np.dot(A1, W2) + b2
  A2 = sigmoid(Z2)

  # 3층(출력층) 계산
  Z3 = np.dot(A2, W3) + b3
  y = identity_function(Z3)

  return y
  
network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)

print(y)

~~>
[0.31682708 0.69627909]