활성화 함수

신경망의 등장

다층 퍼셉트론은 단층 퍼셉트론으로는 계산 할 수 없는 복잡한 함수들을 표현할 수 았다.
다층 퍼셉트론을 층처럼 겹겹이 쌓은 것을 인공 신경망( Artificial Neural Network )이라고 한다.

활성화 함수

• 인공 신경망의 퍼셉트론을 유닛, 노드, 뉴런 이라고 표현
• 퍼셉트론의 결과물은 0 또는 1 로만 출력 되는 것
• 0 이나 1 뿐만이 아닌 유닛이 다양한 계산을 할 수 있게끔 값을 조정해 주는 것이 활성화 함수

퍼셉트론 수식

$z= w_1x_1 + w_2x_2 + b$
식에 의해 퍼셉트론을 구현 하려면 조건이 필요했었다.

함수 $u$는 퍼셉트론이라는 유닛의 결과물을 내기 위한 계단 함수 이 함수 $u$는 퍼셉트론의 활성화 함수라고 한다.

일반화된 뉴런의 수식

함수 $a$를 활성화 함수( Actication Function )라고 하며, 각 입력값에 대한 활성화 함수를 적용시켜 최종적으로 $y$ 값이 결정지어지게 된다.

💡 우리가 여기서 배울건
단순하게 0과 1로만 표현하는 계단 함수 $u$를 넘어서, 다양한 값( 실숫값 ) 으로 표현이 가능한 활성화 함수를 배운다.

뉴런이 값을 다양하게 표현한다는 것의 의미 : 비선형 활성화 함수를 사용하는 이유

• 왜 계단 함수 같은 선형 함수는 활성화 함수로 사용하지 않는가?
  • 예를 들어 활성화 함수가 $a(z) = cz_{(c는 상수)}$
  • 층을 여러 개(3층) 쌓게 되면? $y = a(a(a(z)))$
  • 이는 $y = c^3z$ 로 표현이 가능함
  • 몇 층을 쌓아도 단순하게 상수에 $z$를 곱한 형식으로 표현이 됨
  • 뉴런을 겹겹이 쌓는 의미가 사라진다.
• 비선형 함수를 사용하게 되면?
  • 값의 표현이 다채로워 진다.
  • 층을 쌓거나, 다른 활성화 함수를 사용했을 때 뉴런의 표현( 뉴런의 출력 )이 다채롭게 된다.

활성화 함수

#1 시그모이드($\sigma$)

• $\sigma(z) = \frac{\mathrm{1} }{\mathrm{1} + e^{-z} }$, $z=WX+b$
• $\sigma$는 어떠한 값이 들어오든 항상 0 보다 크고 1 보다 작은 실수를 출력한다.
• 값이 무한대로 커질 수록 1에 가까워 지지만, 절대 1이 되진 않는다.
• 값이 무한대로 작아질 수록 0에 가까워 지지만, 절대 0이되진 않는다.

시그모이드 함수의 의미

• 뉴런의 연산에서는 입력 신호의 출력 강도(세기)를 의미한다.

  • 다음 층에 얼마나 강하게 값을 넘길가를 의미한다.

    출력 강도가 약하면 약할 수록( 0에 가까울 수록 ) 중요하지 않은 값이라 판단
    출력 강도가 강하면 강할 수록( 1에 가까울 수록 ) 중요한 값이라 판단

  • 계단 함수는 단순하게 활성화가 된다(1), 안된다(0)
  • 시그모이드 함수는 이 만큼 강하게 활성화가 된다( 1에 가까운 실수 ), 이 만큼 약하게 활성화가 된다( 0에 가까운 실수 )는 객관적인 수치 를 표현

• 출력( 결과물 출력 - 예측 ) 에서는 0 또는 1 이 될 확률을 의미한다.

  • 0.5를 기준으로 0.5보다 작으면 0으로 분류될 확률이 크다 라는 것을 의미한다.
  • 0.5를 기준으로 0.5보다 크면 1로 분류될 확률이 크다 라는 것을 의미한다.
  • 예를 들어 시그모이드의 출력이 0.4이라면,

    1로 분류될 확률이 40%
    0으로 분류될 확률이 60%

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

# 계단 함수 구현하기
def step_function(z):
	return np.array(z > 0, dtype=np.int)
    
# 시그모이드 함수 구현하기
# 자연상수 e의 지수함수는 넘파이에 np.exp 에 구현 되어 있다.
def sigmoid(z):
	return 1 / (1 + np.exp(-z)) # np.exp(-z) => e의 -z제곱

# 시각화
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(20, 8))
x = np.arange(-5.0, 5.0, 0.1)

ax1.plot(x, step_function(x))
ax1.set_title(`step function')

ax2.plot(x, sigmoid(x))
ax2.set_title('sigmoid function')

plt.show()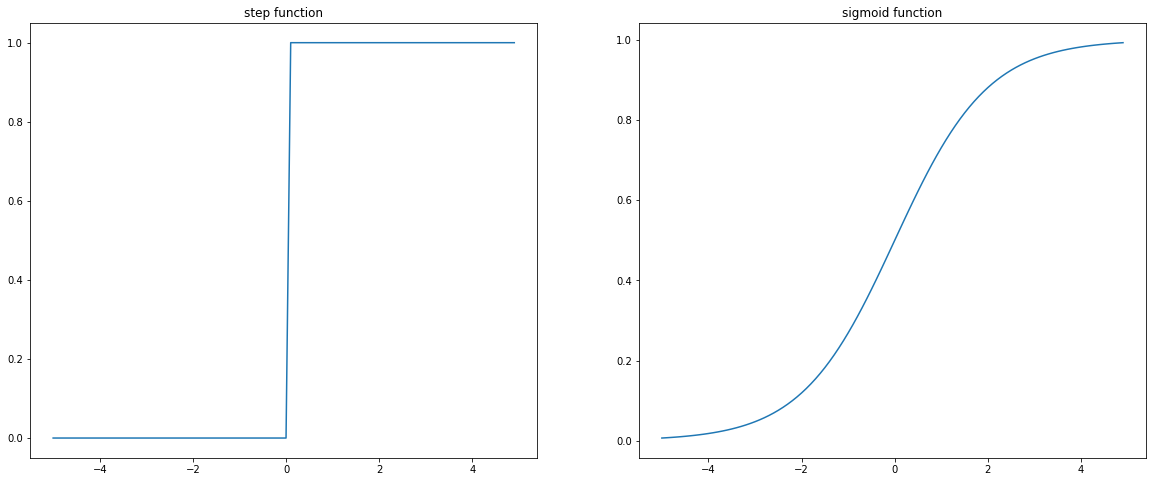

#2 ReLU(Rectified Linear Unit)

• 이미지 처리에 주로 사용되어지는 함수

• 최근에는 다양한 분야에서도 효과를 발휘한다고 알려져 있다.

• 이미지 처리를 위한 CNN알고리즘과 찰떡궁합인 함수

• 입력값이 0 을 넘으면 그 입력을 그대로 출력, 0 이하면 0 을 출력하는 함수

  • 연산을 단순화하면서 필요한 데이터를 강조하는 효과가 있다.

• $relu(x) = \begin{cases} 0\enspace(x \leq 0) \\ x\enspace(x > 0) \end{cases}$

ReLU를 사용하는 의유

• 최근에는 시그모이드 보다는 비선형 직선을 여러 개 연결하는 ReLU를 더 많이 사용하는 추세

  • $\sigma$는 곡선함수라서 연산 비용( CPU나 GPU의 연산 )이 많이 들어간다.
  • 따라서 필요에 따라 ReLU를 여러 개 붙여서 사용하는 것이 도움이 될때가 많다.
  • 물론 데이터에 따라서 종류나 특징에 따라 성능은 달라진다.

• 이미지 처리에서 ReLU를 사용하는 이유

  • 이미지는 항상 0 ~ 255 까지의 정수로 이루어져 있다. ( 채널의 픽셀 값 )
  • 이미지도 신경망의 연산( $WX$ + $b$ )에 따라서 실수의 형태로 출력이 되게 된다.
  • 연산에 의해서 실수화가 되다 보니 음수 값이 등장하기 시작한다.
  • 하지만 이미지에서는 음수 데이터는 사용하지 않는 데이터 이기 때문에, 음수로 연산된 데이터를 0 으로 만들어서 연산의 부담을 줄여준다.
  • 결과론적으로 결과물을 증폭시키는 양수 데이터만 사용하게 되어, 필요 없는 부분은 생각하지 않고, 이미지 처리에 필요한 부분만 생각하게 된다.

# ReLU 함수 구현
# 음수 데이터면 0, 양수 데이터면 해당 데이터가 그대로 출력
def relu(z):
	return np.maximum(0, z) # maximum : 둘 중 큰 값을 출력
    
# 시각화
plt.figure(figsize=(10, 8))
x = np.arange(-0.5, 5.0, 0.1)
plt.title('ReLU Function')
plt.plot(x, relu(x))
plt.show()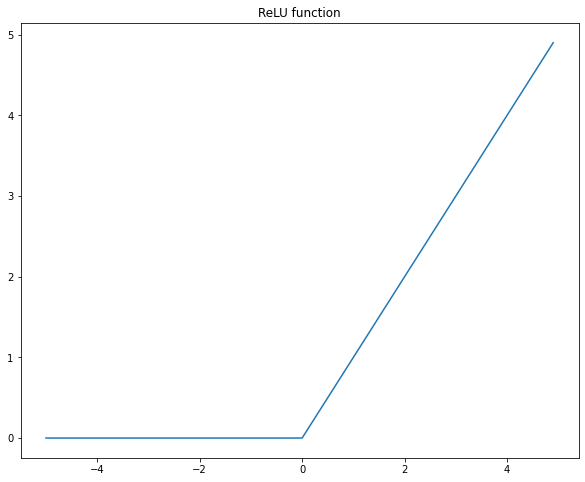

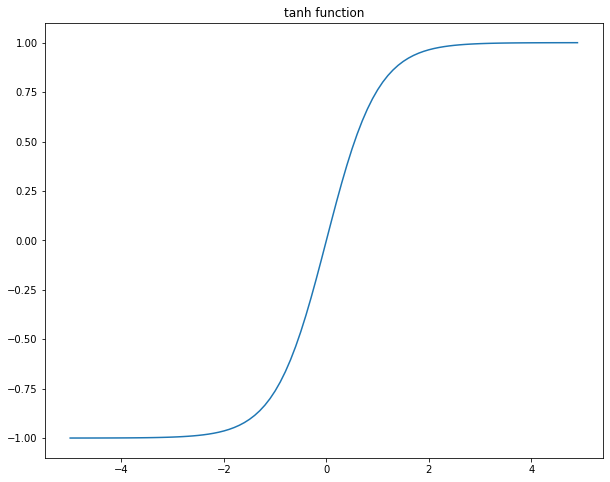
#3 하이퍼볼릭 탄젠트(tanh)

• 텍스트 처리에 주로 사용되어지는 활성화 함수
• 시그모이드($\sigma$)와 비슷한 모양이지만, -1 ~ 1 사이의 값으로 출력

x = np.arange(-0.5, 0.5, 0.1)
plt.figure(figsize=(10, 8))
plt.title('tanh function')
plt.plot(x, np.tanh(x))

plt.show()