미분
-
에서 한 순간의 변화량을 구하는 것
- 가 아주아주 조금 변화가 되었을 때 는 얼마만큼 변화했는가
-
변화량 =
가 아주아주 조금( 만큼 ) 변화 되었을 때
미분 구현
📍 미분의 나쁜 구현
import numpy as np
def numerical_diff(f, x):
# f : 미분 대상 함수 ( 변화량을 구할 함수 )
# x : x인 순간의 변화량을 구하기 위함
h = 1e-50 # 소수점 밑으로 0이 49개
return (f(x+h) - f(x)) / h분모를 0으로 두는 것은 불가능
x인 순간을 구해서 h를 0으로 설정하는 것이 아닌, 0에 아주아주 가까운 숫자로 지정
- 수학적으로 분모는 0이 올 수가 없다.
- 의미적으로도 변화량을 구하는 것이기 때문에 0에 무한히 가깝게 가는 것이지, 0이 아님
💡 너무나 작은 숫자로 나눗셈을 하게 되면, 컴퓨팅 시스템상 부동소숫점 오류가 발생 ( 반올림 오차 )
np.float32(1e-50)
~~>
0.0
1/ np.float32(1e-50) # 1 / 0.0 -> inf
~~>
inf전방차분과 중앙차분을 이용한 미분
📍 향상된 미분 함수
def numerical_diff(f, x):
h = 1e-4 # 0.0001이 가장 적당하다고 알려져 있다고 한다.
return (f(x+h) - f(x-h)) / (2*h)💡 실제 을 집어 넣고 미분을 계산하는 것을 수치미분이라고 한다.
수치미분의 예시
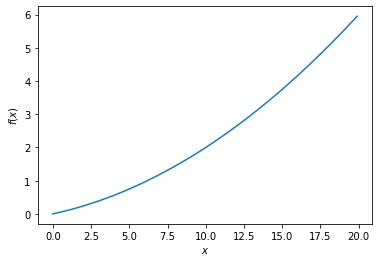
def function_1(x):
return 0.001*x**2 + 0.1*ximport numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
x = np.arange(0.0, 20, 0.1)
y = function_1(x)
plt.xlabel(r'$x$')
plt.ylabel(r'$f(x)$')
plt.plot(x, y)
plt.show()
~~>
print('x가 5일 때의 미분값 : {:.1f}' .format(numerical_diff(function_1, 5)))
print('x가 10일 때의 미분값 : {:.1f}' .format(numerical_diff(finction_1, 10)))
~~>
x가 5일 때의 미분값 : 0.2
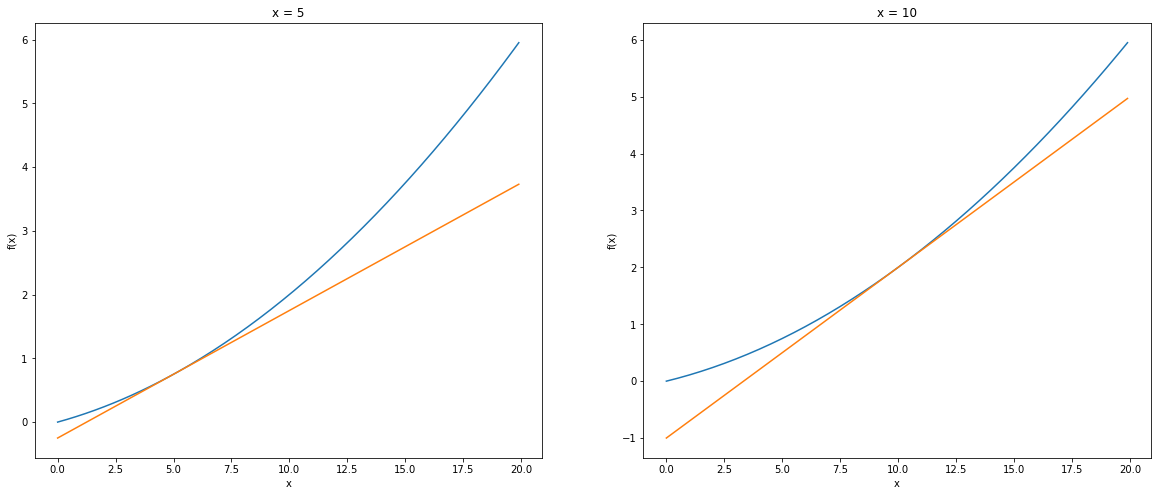
x가 10일 때의 미분값 : 0.3미분값을 이용한 접선 시각화
def tangent_line(f, x):
d = numerical_diff(f, x) # 미분을 통해 기울기를 구한다.
y = f(x) - d*x # 기울기를 활용해서 y값을 구한다.
return lambda t: d*t + y # y값을 토대로 접선을 그린다.
fig, axes = plt.subplots(1, 2, figsize=(20, 8))
x = np.arange(0.0, 20.0, 0.1)
y = function_1(x)
axes[0].set_xlabel('x')
axes[0].set_ylabel('f(x)')
tf = tangent_line(function_1, 5)
y2 = tf(x)
axes[0].plot(x, y)
axes[0].plot(x, y2)
axes[0].set_title('x = 5')
axes[1].set_xlabel('x')
axes[1].set_ylabel('f(x)')
tf = tangent_line(function_1, 10)
y2 = tf(x)
axes[1].plot(x, y)
axes[1].plot(x, y2)
axes[1].set_title('x = 10')
plt.show()
~~>
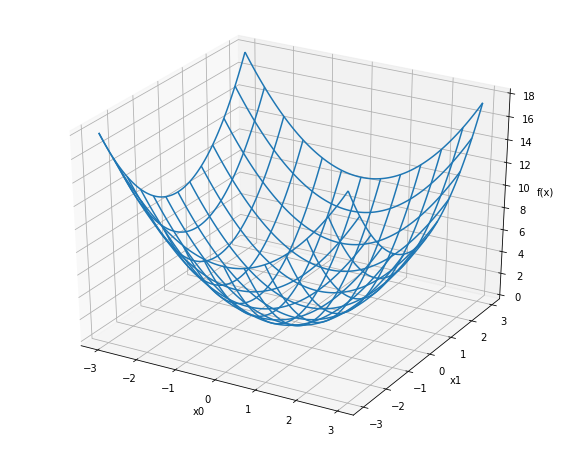
편미분
- 위 예에서는 x( 인수 또는 변수가 된다 ) 1개
- 2개 이상의 인수에 대한 미분은 편미분 이라고 한다.
- 한 쪽만( 인수 하나만 ) 신경써서 미분을 하겠다.
def function_2(x):
# x : numpy 배열
return x[0]**2 + x[1]**2from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
x0 = np.arange(-3, 3, 0.05)
x1 = np.arange(-3, 3, 0.05)
x0, x1 = np.meshgrid(x0, x1)
z = function_2([x0, x1])
ax.plot_wireframe(x=x0, y=x1, z=z, rstride=10, cstride=10)
ax.set_xlabel('x0')
ax.set_ylabel('x1')
ax.set_ylabel('f(x)')
plt.show()
~~>
-
편미분은 한 쪽을 무시한 채로 미분을 하는 것
-
내가 미분하고자 하는 변수를 제외하고는 모두다 상수로 처리
-
상수는 미분하면 0 이 된다.
-
을 미분하면? 은 상수이기 때문에 를 미분하면 가 된다.
-
에서, 로 편미분을 한다면?
- 을 상수처럼 생각을 하게 된다.
- 로 미분하는 꼴이 된다.
- 즉 결과는 를 미분하면?
-
로 편미분을 하고 싶다 -> -> 에 대한 의 편미분값
-
->
문제 1
일 때, 에 대한 편미분 를 구하시오.
def function_tmp1(x0):
return x0**2 + 4.0**2
print('{:.1f}' .format(numerical_diff(function_tmp1, 3.0)))
~~> 6.0✔ 답은 약 6.0이 나오게 된다.
문제 2
일 때, 에 대한 편미분 를 구하시오.답 : 약 8.0
def function_tmp2(x1):
return 3.0**2 + x1**2
print('{:.1f}' .format(numerical_diff(function_tmp2, 4.0)))
~~> 8.0✔ 답은 약 8.0이 나오게 된다.
기울기 배열(gradient)
- 최소 지점에 도달을 할수록 기울기는 완만해진다.
- 기울기가 작아지면 완반해진다.
- 기울기가 높아지게 되면 가파르게 된다.
- 에 대한 기울기와, 에 대한 기울기를 따로 구해서 확인
- 에 대한 기울기와, 에 대한 기울기를 동시에 생각하면 두 방향 모두 고려한 기울기 값을 얻어낼 수가 있다.
- (에 대한 기울기, 에 대한 기울기)
기울기 배열
기울기 벡터
벡터: 방향과 크기를 나타낸 것
def numerical_gradient(f, x):
# f : 편미분 대상 함수
# x : x값이 들어있는 배열 (x0, x1)
h = 1e-4
grads = np.zeros_like(x) # x와 형상이 같은 0으로 채워진 배열을 생성
# 각 x에 대한 편미분을 수행
for idx im range(x.size):
tmp_val = x[idx] # 차례차례 x를 꺼내오기
# f(x+h) 계산
x[idx] = tmp_val + h
fxh1 = f(x)
# f(x-h) 계산
x[idx] = tmp_val - h
fxh2 = f(x)
grads[idx] = (fxh1 - fxh2) / 2*h # 미분 수행
x[idx] = tmp_val # 원래 값으로 복원하기
return gradsresult = numerical_gradient(function_2, np.array([3.0, 4.0]))
print('x = [3, 4] 일 때의 기울기 배열 : {}' .format(result))
~~>
x = [3, 4] 일 때의 기울기 배열 : [6.e-08 8.e-08]
result = numerical_gradient(function_2, np.array([2.0, 3.0]))
print("x = [2, 3] 일 때의 기울기 배열 : {}".format(result))
~~>
x = [2, 3] 일 때의 기울기 배열 : [4.e-08 6.e-08]
result = numerical_gradient(function_2, np.array([1.0, 2.0]))
print("x = [1, 2] 일 때의 기울기 배열 : {}".format(result))
~~>
x = [1, 2] 일 때의 기울기 배열 : [2.e-08 4.e-08]
result = numerical_gradient(function_2, np.array([0.0, 0.0]))
print("x = [0, 0] 일 때의 기울기 배열 : {}".format(result))
~~>
x = [0, 0] 일 때의 기울기 배열 : [0. 0.]# coding: utf-8
# cf.http://d.hatena.ne.jp/white_wheels/20100327/p3
import numpy as np
import matplotlib.pylab as plt
from mpl_toolkits.mplot3d import Axes3D
def _numerical_gradient_no_batch(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x) # x와 형상이 같은 배열을 생성
for idx in range(x.size):
tmp_val = x[idx]
# f(x+h) 계산
x[idx] = float(tmp_val) + h
fxh1 = f(x)
# f(x-h) 계산
x[idx] = tmp_val - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val # 값 복원
return grad
def numerical_gradient(f, X):
if X.ndim == 1:
return _numerical_gradient_no_batch(f, X)
else:
grad = np.zeros_like(X)
for idx, x in enumerate(X):
grad[idx] = _numerical_gradient_no_batch(f, x)
return grad
def function_2(x):
if x.ndim == 1:
return np.sum(x**2)
else:
return np.sum(x**2, axis=1)
def tangent_line(f, x):
d = numerical_gradient(f, x)
print(d)
y = f(x) - d*x
return lambda t: d*t + y
if __name__ == '__main__':
x0 = np.arange(-2, 2.5, 0.25)
x1 = np.arange(-2, 2.5, 0.25)
X, Y = np.meshgrid(x0, x1)
X = X.flatten()
Y = Y.flatten()
grad = numerical_gradient(function_2, np.array([X, Y]) )
plt.figure()
plt.quiver(X, Y, -grad[0], -grad[1], angles="xy",color="#666666")
plt.xlim([-2, 2])
plt.ylim([-2, 2])
plt.xlabel('x0')
plt.ylabel('x1')
plt.grid()
plt.draw()
plt.show()
~~>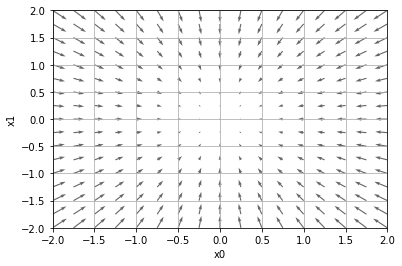
- 을 벡터로 묶어서 표현
- 최소지점으로 가기 위함 의 방향과 크기, 최소지점으로 가기 위함 의 방향과 크기
- 즉 기울기가 크면 클 수록 그 만큼 많이 움직여야 한다.
- 기울기가 가리키는 쪽은 각 장소에서 ( 좌표에서 ) 함수의 출력값 ()의 결과값이 가장 작은 곳
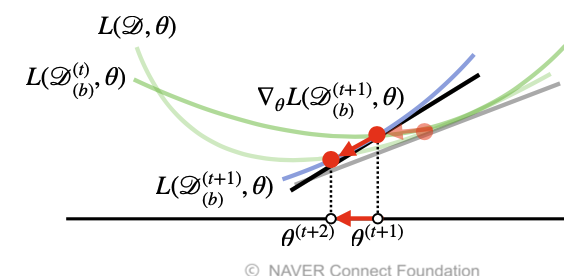
경사하강법 - Gradient Descent ✨✨
- 기울기를 줄여 나가는 방법
- 손실값( Loss )을 최소로 하기 위한 매개변수를 구하는 과정
- **최적화(Optimization)라고 한다.
- 신경망에서의 매개변수는 가중치와 편향
- Loss를 최소화 하기 위한 가중치와 편향을 구하는 과정을 최적화라고 하고, 경사하강법은 최적화 기법의 일종
경사하강법의 원리
- 현 위치에서 기울어진 방향으로 **일정 거리 만큼 이동( Learning Rate )
- 이동한 곳에서도 미분을 통해 기울기를 구하고, 기울기를 구한 방향으로 이동
- 이 과정을 최소화가 되는 지점을 찾을 때 까지 반복( step )
- : Learning Rate( 하이퍼 파라미터 )
- 위 과정을 매개변수 업데이트라고 한다.
경사하강법 구현
def gradient_decent(f, init_x, lr=0.01, step_num=100):
# f : 경사하강법을 수행할 함수
# init_x : x의 최초 지점
# lr : learning_rate
# step_num : 경사하강법 수행 횟수
x = init_x
for i in range(step_num): # 기울기 배열을 구한다.
grad = numerical_gradient(f, x) # 현 위치에서의 기울기 배열을 구한다.
print('x 좌표 : {} / 기울기 : {}' .format(x, grads))
x = x- lr*grads
return xdef function_2(x):
return x[0]**2 + x[1]**2
init_x = np.array([-3.0, 4.0])
gradient_descent(function_2, init_x, lr=0.1, step_num=100)
~~>
x 좌표 : [-3. 4.] / 기울기 : [-6. 8.]
x 좌표 : [-2.4 3.2] / 기울기 : [-4.8 6.4]
x 좌표 : [-1.92 2.56] / 기울기 : [-3.84 5.12]
x 좌표 : [-1.536 2.048] / 기울기 : [-3.072 4.096]
x 좌표 : [-1.2288 1.6384] / 기울기 : [-2.4576 3.2768]
x 좌표 : [-0.98304 1.31072] / 기울기 : [-1.96608 2.62144]
x 좌표 : [-0.786432 1.048576] / 기울기 : [-1.572864 2.097152]
x 좌표 : [-0.6291456 0.8388608] / 기울기 : [-1.2582912 1.6777216]
x 좌표 : [-0.50331648 0.67108864] / 기울기 : [-1.00663296 1.34217728]
x 좌표 : [-0.40265318 0.53687091] / 기울기 : [-0.80530637 1.07374182]
x 좌표 : [-0.32212255 0.42949673] / 기울기 : [-0.64424509 0.85899346]
x 좌표 : [-0.25769804 0.34359738] / 기울기 : [-0.51539608 0.68719477]
x 좌표 : [-0.20615843 0.27487791] / 기울기 : [-0.41231686 0.54975581]
x 좌표 : [-0.16492674 0.21990233] / 기울기 : [-0.32985349 0.43980465]
x 좌표 : [-0.1319414 0.17592186] / 기울기 : [-0.26388279 0.35184372]
x 좌표 : [-0.10555312 0.14073749] / 기울기 : [-0.21110623 0.28147498]
x 좌표 : [-0.08444249 0.11258999] / 기울기 : [-0.16888499 0.22517998]
x 좌표 : [-0.06755399 0.09007199] / 기울기 : [-0.13510799 0.18014399]
x 좌표 : [-0.0540432 0.07205759] / 기울기 : [-0.10808639 0.14411519]
x 좌표 : [-0.04323456 0.05764608] / 기울기 : [-0.08646911 0.11529215]
x 좌표 : [-0.03458765 0.04611686] / 기울기 : [-0.06917529 0.09223372]
x 좌표 : [-0.02767012 0.03689349] / 기울기 : [-0.05534023 0.07378698]
x 좌표 : [-0.02213609 0.02951479] / 기울기 : [-0.04427219 0.05902958]
x 좌표 : [-0.01770887 0.02361183] / 기울기 : [-0.03541775 0.04722366]
x 좌표 : [-0.0141671 0.01888947] / 기울기 : [-0.0283342 0.03777893]
x 좌표 : [-0.01133368 0.01511157] / 기울기 : [-0.02266736 0.03022315]
x 좌표 : [-0.00906694 0.01208926] / 기울기 : [-0.01813389 0.02417852]
x 좌표 : [-0.00725355 0.00967141] / 기울기 : [-0.01450711 0.01934281]
x 좌표 : [-0.00580284 0.00773713] / 기울기 : [-0.01160569 0.01547425]
x 좌표 : [-0.00464228 0.0061897 ] / 기울기 : [-0.00928455 0.0123794 ]
x 좌표 : [-0.00371382 0.00495176] / 기울기 : [-0.00742764 0.00990352]
x 좌표 : [-0.00297106 0.00396141] / 기울기 : [-0.00594211 0.00792282]
x 좌표 : [-0.00237684 0.00316913] / 기울기 : [-0.00475369 0.00633825]
x 좌표 : [-0.00190148 0.0025353 ] / 기울기 : [-0.00380295 0.0050706 ]
x 좌표 : [-0.00152118 0.00202824] / 기울기 : [-0.00304236 0.00405648]
x 좌표 : [-0.00121694 0.00162259] / 기울기 : [-0.00243389 0.00324519]
x 좌표 : [-0.00097356 0.00129807] / 기울기 : [-0.00194711 0.00259615]
x 좌표 : [-0.00077884 0.00103846] / 기울기 : [-0.00155769 0.00207692]
x 좌표 : [-0.00062308 0.00083077] / 기울기 : [-0.00124615 0.00166153]
x 좌표 : [-0.00049846 0.00066461] / 기울기 : [-0.00099692 0.00132923]
x 좌표 : [-0.00039877 0.00053169] / 기울기 : [-0.00079754 0.00106338]
x 좌표 : [-0.00031901 0.00042535] / 기울기 : [-0.00063803 0.00085071]
x 좌표 : [-0.00025521 0.00034028] / 기울기 : [-0.00051042 0.00068056]
x 좌표 : [-0.00020417 0.00027223] / 기울기 : [-0.00040834 0.00054445]
x 좌표 : [-0.00016334 0.00021778] / 기울기 : [-0.00032667 0.00043556]
x 좌표 : [-0.00013067 0.00017422] / 기울기 : [-0.00026134 0.00034845]
x 좌표 : [-0.00010453 0.00013938] / 기울기 : [-0.00020907 0.00027876]
x 좌표 : [-8.36277945e-05 1.11503726e-04] / 기울기 : [-0.00016726 0.00022301]
x 좌표 : [-6.69022356e-05 8.92029808e-05] / 기울기 : [-0.0001338 0.00017841]
x 좌표 : [-5.35217885e-05 7.13623846e-05] / 기울기 : [-0.00010704 0.00014272]
x 좌표 : [-4.28174308e-05 5.70899077e-05] / 기울기 : [-8.56348616e-05 1.14179815e-04]
x 좌표 : [-3.42539446e-05 4.56719262e-05] / 기울기 : [-6.85078892e-05 9.13438523e-05]
x 좌표 : [-2.74031557e-05 3.65375409e-05] / 기울기 : [-5.48063114e-05 7.30750819e-05]
x 좌표 : [-2.19225246e-05 2.92300327e-05] / 기울기 : [-4.38450491e-05 5.84600655e-05]
x 좌표 : [-1.75380196e-05 2.33840262e-05] / 기울기 : [-3.50760393e-05 4.67680524e-05]
x 좌표 : [-1.40304157e-05 1.87072210e-05] / 기울기 : [-2.80608314e-05 3.74144419e-05]
x 좌표 : [-1.12243326e-05 1.49657768e-05] / 기울기 : [-2.24486651e-05 2.99315535e-05]
x 좌표 : [-8.97946606e-06 1.19726214e-05] / 기울기 : [-1.79589321e-05 2.39452428e-05]
x 좌표 : [-7.18357285e-06 9.57809713e-06] / 기울기 : [-1.43671457e-05 1.91561943e-05]
x 좌표 : [-5.74685828e-06 7.66247770e-06] / 기울기 : [-1.14937166e-05 1.53249554e-05]
x 좌표 : [-4.59748662e-06 6.12998216e-06] / 기울기 : [-9.19497325e-06 1.22599643e-05]
x 좌표 : [-3.67798930e-06 4.90398573e-06] / 기울기 : [-7.35597860e-06 9.80797146e-06]
x 좌표 : [-2.94239144e-06 3.92318858e-06] / 기울기 : [-5.88478288e-06 7.84637717e-06]
x 좌표 : [-2.35391315e-06 3.13855087e-06] / 기울기 : [-4.70782630e-06 6.27710174e-06]
x 좌표 : [-1.88313052e-06 2.51084069e-06] / 기울기 : [-3.76626104e-06 5.02168139e-06]
x 좌표 : [-1.50650442e-06 2.00867256e-06] / 기울기 : [-3.01300883e-06 4.01734511e-06]
x 좌표 : [-1.20520353e-06 1.60693804e-06] / 기울기 : [-2.41040707e-06 3.21387609e-06]
x 좌표 : [-9.64162827e-07 1.28555044e-06] / 기울기 : [-1.92832565e-06 2.57110087e-06]
x 좌표 : [-7.71330261e-07 1.02844035e-06] / 기울기 : [-1.54266052e-06 2.05688070e-06]
x 좌표 : [-6.17064209e-07 8.22752279e-07] / 기울기 : [-1.23412842e-06 1.64550456e-06]
x 좌표 : [-4.93651367e-07 6.58201823e-07] / 기울기 : [-9.87302734e-07 1.31640365e-06]
x 좌표 : [-3.94921094e-07 5.26561458e-07] / 기울기 : [-7.89842188e-07 1.05312292e-06]
x 좌표 : [-3.15936875e-07 4.21249167e-07] / 기울기 : [-6.31873750e-07 8.42498333e-07]
x 좌표 : [-2.52749500e-07 3.36999333e-07] / 기울기 : [-5.05499000e-07 6.73998667e-07]
x 좌표 : [-2.02199600e-07 2.69599467e-07] / 기울기 : [-4.04399200e-07 5.39198933e-07]
x 좌표 : [-1.61759680e-07 2.15679573e-07] / 기울기 : [-3.23519360e-07 4.31359147e-07]
x 좌표 : [-1.29407744e-07 1.72543659e-07] / 기울기 : [-2.58815488e-07 3.45087317e-07]
x 좌표 : [-1.03526195e-07 1.38034927e-07] / 기울기 : [-2.07052390e-07 2.76069854e-07]
x 좌표 : [-8.28209562e-08 1.10427942e-07] / 기울기 : [-1.65641912e-07 2.20855883e-07]
x 좌표 : [-6.62567649e-08 8.83423532e-08] / 기울기 : [-1.32513530e-07 1.76684706e-07]
x 좌표 : [-5.30054119e-08 7.06738826e-08] / 기울기 : [-1.06010824e-07 1.41347765e-07]
x 좌표 : [-4.24043296e-08 5.65391061e-08] / 기울기 : [-8.48086591e-08 1.13078212e-07]
x 좌표 : [-3.39234636e-08 4.52312849e-08] / 기울기 : [-6.78469273e-08 9.04625697e-08]
x 좌표 : [-2.71387709e-08 3.61850279e-08] / 기울기 : [-5.42775418e-08 7.23700558e-08]
x 좌표 : [-2.17110167e-08 2.89480223e-08] / 기울기 : [-4.34220335e-08 5.78960446e-08]
x 좌표 : [-1.73688134e-08 2.31584178e-08] / 기울기 : [-3.47376268e-08 4.63168357e-08]
x 좌표 : [-1.38950507e-08 1.85267343e-08] / 기울기 : [-2.77901014e-08 3.70534686e-08]
x 좌표 : [-1.11160406e-08 1.48213874e-08] / 기울기 : [-2.22320811e-08 2.96427748e-08]
x 좌표 : [-8.89283245e-09 1.18571099e-08] / 기울기 : [-1.77856649e-08 2.37142199e-08]
x 좌표 : [-7.11426596e-09 9.48568795e-09] / 기울기 : [-1.42285319e-08 1.89713759e-08]
x 좌표 : [-5.69141277e-09 7.58855036e-09] / 기울기 : [-1.13828255e-08 1.51771007e-08]
x 좌표 : [-4.55313022e-09 6.07084029e-09] / 기울기 : [-9.10626043e-09 1.21416806e-08]
x 좌표 : [-3.64250417e-09 4.85667223e-09] / 기울기 : [-7.28500835e-09 9.71334446e-09]
x 좌표 : [-2.91400334e-09 3.88533778e-09] / 기울기 : [-5.82800668e-09 7.77067557e-09]
x 좌표 : [-2.33120267e-09 3.10827023e-09] / 기울기 : [-4.66240534e-09 6.21654046e-09]
x 좌표 : [-1.86496214e-09 2.48661618e-09] / 기울기 : [-3.72992427e-09 4.97323236e-09]
x 좌표 : [-1.49196971e-09 1.98929295e-09] / 기울기 : [-2.98393942e-09 3.97858589e-09]
x 좌표 : [-1.19357577e-09 1.59143436e-09] / 기울기 : [-2.38715153e-09 3.18286871e-09]
x 좌표 : [-9.54860614e-10 1.27314749e-09] / 기울기 : [-1.90972123e-09 2.54629497e-09]
x 좌표 : [-7.63888491e-10 1.01851799e-09] / 기울기 : [-1.52777698e-09 2.03703598e-09]
array([-6.11110793e-10, 8.14814391e-10])import numpy as np
import matplotlib.pyplot as plt
def gradient_descent(f, init_x, lr=0.01, step_num=100):
x = init_x
x_history = []
for i in range(step_num):
x_history.append(x.copy())
grad = numerical_gradient(f, x)
x -= lr*grad
return x, np.array(x_history)
init_x = np.array([-0.3, 4.0])
lr = 0.1
step_num = 20
x, x_history = gradient_descent(finction_2, init_x, lr=lr, step_num=step_num)
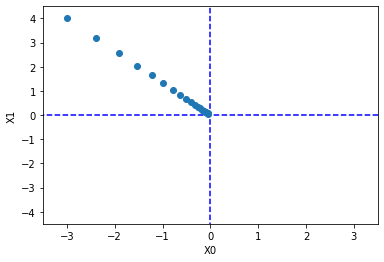
plt.plot([-5, 5], [0, 0], '--b')
plt.plot([0, 0], [-5, 5], '--b')
plt.plot(x_history[:, 0], x_history[:, 1], 'o')
plt.xlim(-3.5, 3.5)
plt.ylim(-4.5, 4.5)
plt.xlabel('x0')
plt.ylabel('x1')
plt.show()
~~>
학습률(Learning Rate)이 너무 크거나 작으면 벌어지는 일들
- Learning Rate가 너무 크면 좌표가 발산
- Learning Rate가 너무 작으면 갱신이 거의 안된다.
💡 학습률이 너무 큰 예. lr = 10.0
init_x = np.array([-3.0, 4.0])
result, _ = gradient_descent(function_2, init_x=init_x, lr=10.0, step_num=100)
print('Learing Rate 10.0 : {}' .format(result))
~~>
Learning Rate 10.0 : [-2.58983747e+13 -1.29524862e+12]💡 학습률이 너무 작은 예. lr = 1e-10
init_x = np.array([-3.0, 4.0])
result, _ = gradient_descent(function_2, init_x=init_x, lr=1e-10, step_num=100)
print('Learning Rate 1e-10 : {}'. format(result))
~~>
Learning Rate 1e-10 : [-2.99999994 3.99999992]학습이 가능한 신경망 만들기
-
신경망의 학습이란?
Loss() 값을 최소화 시키는 가중치()와 편향()을 구한다.
-
미분은 어떻게 쓰일까?
,
📍 실습에 필요한 함수들
import numpy as np
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def softmax(x):
if x.ndim == 2:
x = x.T
x = x - np.max(x, axis=0)
y = np.exp(x) / np.sum(np.exp(x), axis=0)
return y.T
x = x - np.max(x) # 오버플로 대책
return np.exp(x) / np.sum(np.exp(x))
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
# 훈련 데이터가 원-핫 벡터라면 정답 레이블의 인덱스로 반환
if t.size == y.size:
t = t.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
def numerical_gradient(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x)
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
while not it.finished:
idx = it.multi_index
tmp_val = x[idx]
x[idx] = float(tmp_val) + h
fxh1 = f(x) # f(x+h)SimpleNet
- 입력을 두개 받는
[x1, x2]3개의 뉴런을 가진 신경망 - 편향 고려 x, 가중치만 고려
class SimpleNet:
def __init__(self):
# 신경망이 초기에 가지고 있어야 할 매개변수를 세팅
# 신경망 매개변수 초기화 작업을 생성자인 __init__ 매소드에서 수행
# 1) 정규분포 랜덤값 * 0.01 (실무에서는 사용이 안된다한다, 공부할 때만 사용)
# 2) 카이밍 히 초깃값( He 초깃값 ) - ReLU를 activation function으로 쓸 때 자주 사용
# 3) 시비에르 초깃값( Xavier 초깃값 ) - sigmoid를 activation function으로 쓸 때 자주 사용
self.W = np.random.randn(2, 3) # 가중치를 랜덤하게 정규분포로 초기화( 원래 0.01 곱해야 하는데 보기가 좀 그래서 넣지 않았다. )
def predict(self, x):
# 손실(Loss)을 구할 때 필요한 것
# 1. 예측값(y)
# 2. 정답(t)
# 3. loss 측정 함수( cross_entropy_error )
z = self.predict(x)
y = softmax(z)
loss = cross_entropy_error(y, t)
return lossnet = SimpleNet()
print('가중치 : \n{}' .format(net.W))
~~>
가중치 :
[[ 1.81509164 -1.47779898 -0.44327992]
[ 1.1835035 0.70338014 1.76561574]]
x = np.array([0.6, 0.9]) # x는 임의로 설정
p = net.predict(x)
print('예측값 : {}' .format(p))
~~>
예측값 : [ 2.15420814 -0.25363727 1.32308622]📍 Loss 구해보기
t = np.array([1, 0, 0])
t_error = np.array([0, 1, 0])
print('정답이 0일 때의 loss : {:.3f}' .format(net.loss(x, t)))
print('정답이 1일 때의 loss : {:.3f}' .format(net.loss(x, t_error)))
~~>
정답이 0 일 때의 loss : 0.422
정답이 1 일 때의 loss : 2.830# 1. W에 대한 Loss구하기 위한 함수
# dL / dW
# 결론적으로는 net.loss를 미분할 함수를 따로 만들어야 한다. ( W에 대한... )
def f(W):
return net.loss(x, t)
# 혹은
# loss_W = lambda W : net.loss(x, t)
# Loss를 구하는 함수 f에 대한 모든 W들의 기울기를 구할 수 있다.
# W의 각 원소에 대한 편미분이 수행된다.
dW = numerical_gradient(f, net.W)
print(dW)
~~>
[[-0.35356551 0.11583533 0.23773018]
[-0.53034826 0.173753 0.35659526]]💡 이 만큼 증가하면 Loss가 0.2 만큼 감소한다.
💡 이 만큼 증가하면 Loss가 0.05 만큼 증가한다.
학습이 가능한 MNIST 신경망 구현
-
2층 신경망
-
1층 은닉층의 뉴런 개수 100개
활성화 함수로 시그모이드 함수를 사용
-
2층 출력층의 뉴런 개수 10개
softmax를 사용
-
loss는 cross entropy error 사용
-
predict에서 softmax를 사용
-
클래스 내부에 기울기 배열을 구하는 numerical_gradient_params를 구현
-
경사하강법을 여기서 구현하지 않는다.
class TwoLayerNet:
def __init__:(self, input_size, hidden_size, output_size, weight_init_std=0.01):
'''
input_size : 입력 데이터 shape(N, 28*28)
hidden_size : 은닉층의 뉴런 개수
output_size : 출력층의 뉴런 개수
weight_init_std : 정규 분포 랜덤값에 표준편차 0.01를 적용하기 위함
'''
self.params = {}
# 1층 매개변수 마련하기
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
# 2층 매개변수 마련하기
self.params['W2'] = weight_init_std * np.random.randn(hiddenP_size, output_size)
self.params['b2'] = np.zeros(output_size)
def predict(self, x):
# 매개변수 가져오기
W1, b1, W2, b2 = self.params['W1'], self.params['b1'], self.params['W2'], self.params['b2']
# z = WX+b
# activation 적용하기
# 1층 은닉층 계산
z1 = np.dot(x, W1) + b1
a1 = sigmoid(z1)
# 2층 출력층 계층
z2 = np.dot(a1, W2) + b2
y = softmax(z2)
return y
def loss(self, x, t):
# 1. 예측값
# 예측? predict
y = self.predict(x)
# 2. loss 함수 적용
loss_val = cross_entropy_error(y, t)
return loss_val
# 미분(numerical_gradient)을 이용한 "각 매개변수 별 기울기 배열 구하기"
def numerical_gradient_params(self, x, t):
# 각 층에서 구해지는 기울기를 저장할 딕셔너리
# 저장하는 이유 : 각 매개변수의 기울기를 저장 해야만 나중에 경사하강법을 수행할 수 있다.
grads = {}
# dL / dW1
# dL / db1
# dL / dW2
# dL / db2
print("---미분 시작---")
# 각 매개변수들에 대한 미분값을 구해낼 "미분 대상 함수"
loss_param_f = lambda p : self.loss(x, t)
# 1층 매개변수들에 대한 기울기 구하기( loss에 대한 W1, b1의 기울기를 grads에 저장 )
grads["W1"] = numerical_gradient(loss_param_f, self.params["W1"]) # W1에 대한 Loss의 변화량(기울기, 미분값)
grads["b1"] = numerical_gradient(loss_param_f, self.params["b1"]) # b1에 대한 Loss의 변화량(기울기, 미분값)
# 2층 매개변수들에 대한 기울기 구하기( loss에 대한 W2, b2의 기울기를 grads에 저장 )
grads["W2"] = numerical_gradient(loss_param_f, self.params["W2"]) # W2에 대한 Loss의 변화량(기울기, 미분값)
grads["b2"] = numerical_gradient(loss_param_f, self.params["b2"]) # b2에 대한 Loss의 변화량(기울기, 미분값)
print("---미분 끝---")
return grads신경망 간단하게 만들어서 테스트 해보기
💡 신경망을 구축하고 나서 신경망 자체를 이해하는데 제일 좋은 방법은 매개변수( 가중치와 편향 )의 개수를 세는 것이 제일 좋다.
📍 신경망 생성
input_size = 28 * 28
hidden_size = 100
output_size = 10
net = TwoLayerNet(input_size, hidden_size, output_size)
net.params['W1'],shape, net.params['b1'].shape
~~>
((784, 100), (100, ))✨ 1층에는 총 784 * 100 + 100 => 78500개
net.params['W2'].shape, net.params['b2'].shape
~~>
((100, 10), (10, ))✨ 2층에는 총 100 * 10 + 10 => 1010개
✨ 1층과 2층의 매개변수의 총 개수 : 79510개의 매개변수가 존재한다.
📍 신경망에 오류가 있는지 없는지 확인
x = np.random.rand(100, 28*28) # BATCH_SIZE = 100
y = net.predict(x)
x.shape, y.shape
~~>
((100, 784), (100, 10))MNIST 데이터 로딩과 전처리
데이터 로드
from tensorflow.keras import datasets
mnist = datasets.mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train.shape, y_train.shape
~~>
((60000, 28, 28), (60000, ))데이터 전처리
y_train, y_test: OHE이 되어야 한다.( 안해도 상관 없음 )x_train, x_test:(N, 28*28)형태로 평탄화 되어야 한다.
📍 y_train, y_test One Hot Encoding
import tensorflow as tf
y_train_one_hot = tf.one_hot(y_train, 10).numpy()
y_test_one_hot = tf.one_hot(y_test, 10).numpy()
y_train_one_hot.shape, y_test_one_hot.shape
~~>
((60000, 10), (10000, 10))📍 x_train, x_test 평탄화 시키기( N, 28*28 ) 만들기
x_train = x_train.reshape(x_train.shape[0], -1)
x_test = x_test.reshape(x_tet.shape[0], -1)
x_train.shape, x_test.shape
~~>
((60000, 784), (10000, 784))이미지 데이터 정규화
- 이미지 데이터는 항상 0 ~ 255 사이의 값을 갖는다.
- 0부터 255라는 숫자의 차이는 매우 큰 데이터 끼리의 차이이기 때문에 0 ~ 1 사이로 정규화
- 255.0 으로 나누어서 최소를 0으로, 최대를 1로 갖는 이미지로 만들어 주기
- 거의 일반적으로 입력 이미지의 픽셀 값을 0 ~ 1사이로 맞추는게 제일 괜찮다.
x_train = x_train / 255.0
x_test = x_test / 255.훈련을 하기 위한 하이퍼 파라미터 설정하기
- 미니 배치 개수 선정
- 훈련 반복 횟수 설정 👉 경사하강법 적용 횟수
- 학습률 선정
iter_nums = 10000 # 반복 횟수 설정
train_size = x_train.shape[0]
batch_size = 100 # 미니 배치 설정
learning_rate = 0.1 # 학습률 선정
network = TwoLayerNet(input_size, hidden_size, output_size) # 신경망 만들기- 반복이 돌아가는 진행 상황을 시각화해서 도와주는 패키지
# 반복문 돌릴 때 진행 상황을 프로그래스 바로 시각화해서 도와주는 패키지
from tqdm import tqdm_notebook
# a = input("실행 하면 안됨 :(Y/N)")
# a = a.upper()
# if a == 'N':
# break;
for i in tqdm_notebook(range(iter_nums)):
# 1. 미니 배치 인덱스 선정(마스크 만들기)
batch_mask = np.random.choice(train_size, batch_size) # train_size(60000)개 중 batch_size(100)개 만큼의 랜덤한 인덱스 선정
# 미니 배치 만들기
x_batch = x_train[batch_mask]
t_batch = y_train[batch_mask]
'''
각 배치 마다의 매개변수 기울기를 계산
numerical_gradient_params에서 하는 일
1. 예측값 구하기(x를 가지고)
2. cross_entropy_error를 이용한 loss 구하기
3. 구해진 Loss값을 이용해 미분을 수행하기(numerical_gradient), 각 매개변수에 대한 기울기를 grads에 저장
'''
grads = network.numerical_gradient_params(x_batch, t_batch)
# 기울기를 구했으면...? 경사하강법을 한다.
# grads 딕셔너리의 key 값이 params 딕셔너리의 key 값과 똑같다.
keys = ['W1', 'W2', 'b1', 'b2']
for key in keys:
# network.params[key] = network.params[key] - (learning_rate * grads[key])
network.params[key] -= learning_rate * grads[key] # 위에 꺼랑 똑같은 것
# 갱신된 loss 확인
loss = network.loss(x_batch, t_batch)
print('Step {} -> Loss : {}' .format(i+1, loss))📌 연산량이 많다.
-
1회 훈련할 때 컴퓨터가 계산해야 할 양
기본 매개변수의 개수 : 79,510개( 이미지 1장에 대한 매개변수 개수 )
배치( 100개 )를 사용하고 있기 때문에 1회당 진행할 미분이 : 7,951,000회 -
미분 연산이 문제가 된다.
-
미분을 하는 이유는 기울기( 변화량, 미분값 )를 구하기 위함
-
미분을 하지 않고 미분값을 구할 수 있는 방법이 있을까?
✨✨✨ 오차역전파를 이용하면 가능