심슨의 역설
: 각 부분에 대한 평균이 크다고 하여 전체에 대한 평균까지는 크지 않다는 의미
즉, 각 변수를 신경쓰지 않고 전체 통계결과를 유추할 때 일어나는 오류
심슨의 역설은 백분율 형태의 통계에서 자주 발생한다.
각 부분의 통계적 결과와 전체의 통계적 결과가 다른 상황인데,
아래 예시를 보자. 나무위키 예시 가져옴
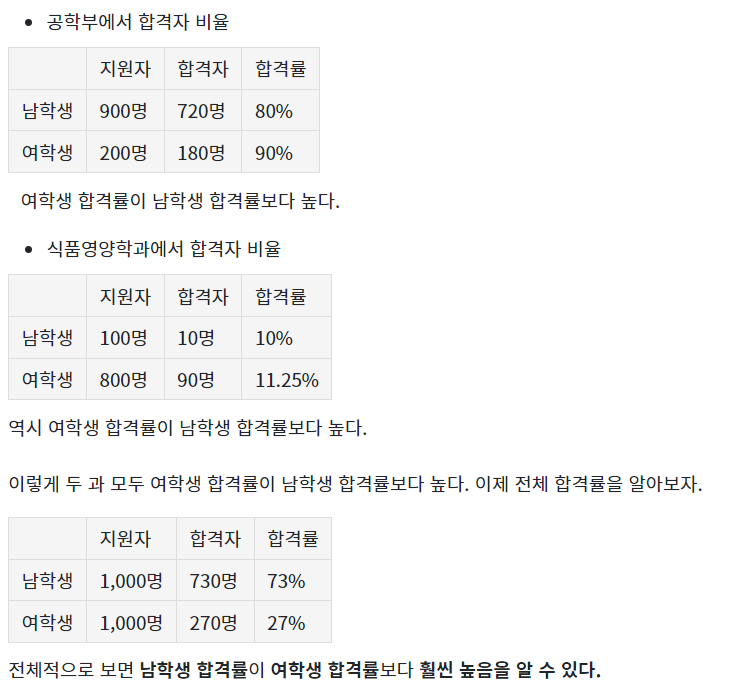
개별 학부의 성별 합격자 비율과 전체 성별 합격자 비율이 다르다.
전체를 보았을 때 각 학부의 남성의 합격률이 높을 것으로 예상했지만, 모두 여성이 남성보다 합격률이 높았다.
❓이러한 경우 어떤 결론을 내릴 수 있을까? 어떻게 내려야 할까?
심슨의 역설은 다음과 같은 조건에서 자주 발생한다. 출처
1. 최소 1개 이상의 confounding variable을 고려하지 않았다.
2. 실험 대상이 되는 그룹 내에서 confounding variable 의 불균형적인 할당이 있었다.여기서 confounding variable은 결과에 영향을 주는 핵심변수 라는 뜻으로 혼재변수, 혼인변인, 교란변수 등 다양한 명칭으로 불린다.
위와 같은 역설은 모수가 큰 결과로 평균이 끌려가는 경향이 발생하기 때문이다.
즉, 각 부분의 샘플의 크기와 비율이 다름에도 불구하고, 가중치를 주지 않아서 자연스럽게 전체 결과에서는 가중 평균이 적용되었기 때문이다.
따라서 분석 목적에 혼재변수가 없도록 결론을 도출하기 위해서는 '분석의 목표와 핵심이 되는 변수를 파악하고, 이 필수적인 요소를 고려해 올바른 결과를 내리기 위해 노력하는 것.'
따라서 데이터를 분석할 때, 전체에 대한 결론이 언제나 개별 집단에 그대로 적용되는 것이 아니라는 것을 기억하고, 전체적인 경향/흐름/추세로 판단하면 안된다. 전체와 부분을 비교하고 관점 별로 교차하여 분석하는 것이 통계적 오유를 벗어날 수 있는 방법이다.
