3.1 Optimal policy - more details

Optimal policy(derivation)

As we have learned, the optimal policy is a function that maximizes the state value function. The state value function focuses on maximizing the reward from the current state. But, how can we maximize the state value function? let's dive into equation.

In the equation, we can see the policy : $p(a_t|s_t)$. Our goal is to find the policy maximizing the equation.

$\mathrm{Goal} = \argmax\limits_{p(a_t|s_t)} \int\limits_{a_t}Q(s_t,a_t)p(a_t|s_t)da_t$
If we apply Bellman equation to Q, we know that Q has every future policy inside.

$Q(s_t,a_t) = p(a_{t+1}|s_{t+1})p(a_{t+2}|s_{t+2})...\ \ \ \ \ \ \ \ \ << \ \mathrm{by\ bayesian \ rule}$
Here is more detail about bayesian rule:

We'll denote the optimal policy as $p^*$, and it's corresponding action value function as $Q^*$, when $Q^*$ reflects every future optimal policy. And let's assume that we have already found the optimal policy for future actions.
Then, we need to focus on current policy only : $p(a_t|s_t)$.

let’s find probability distribution maximizing state value function.

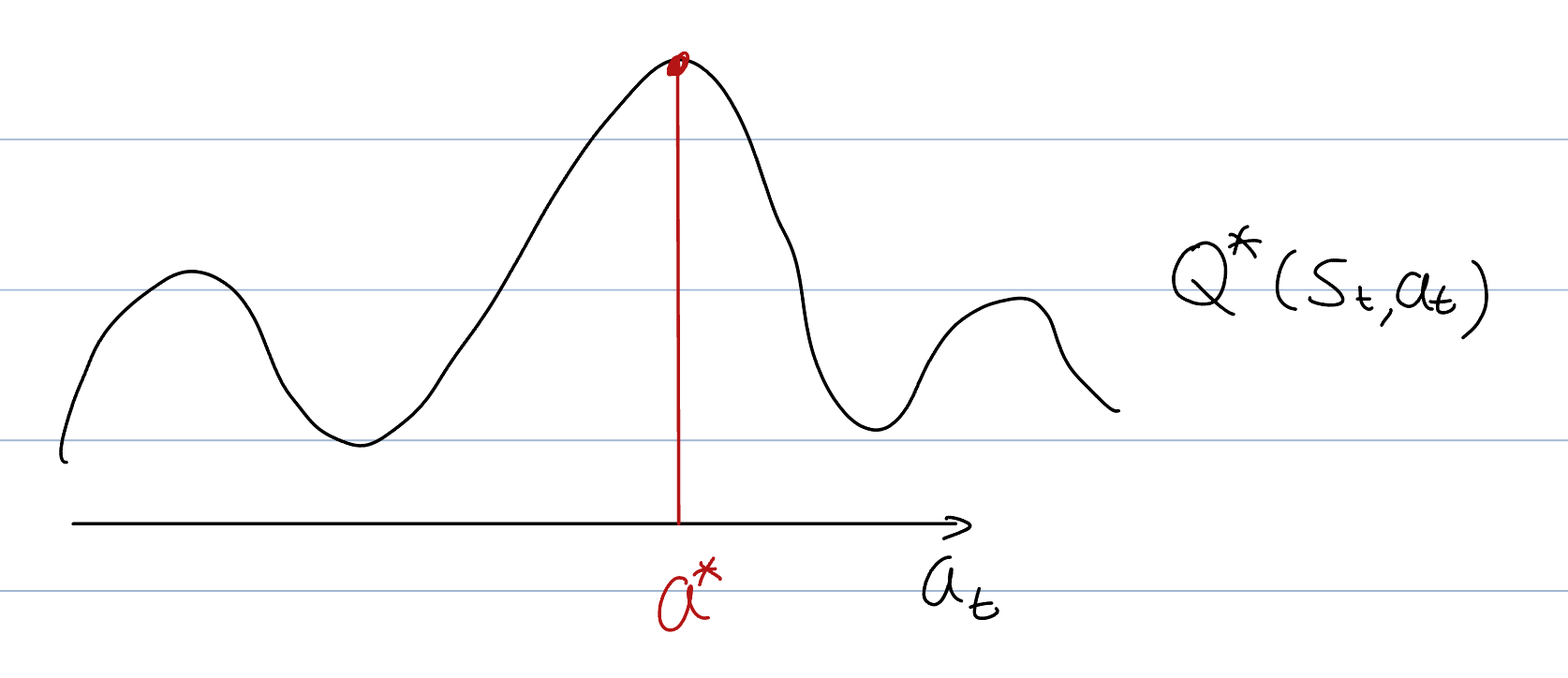
The state value function's equation is integral, implying that the optimal policy (probability) must yield only $a^*$. This is possible only if the probability distribution is a delta function. A delta function is unique in that it is concentrated at a single point yet still retains an integral value of 1.

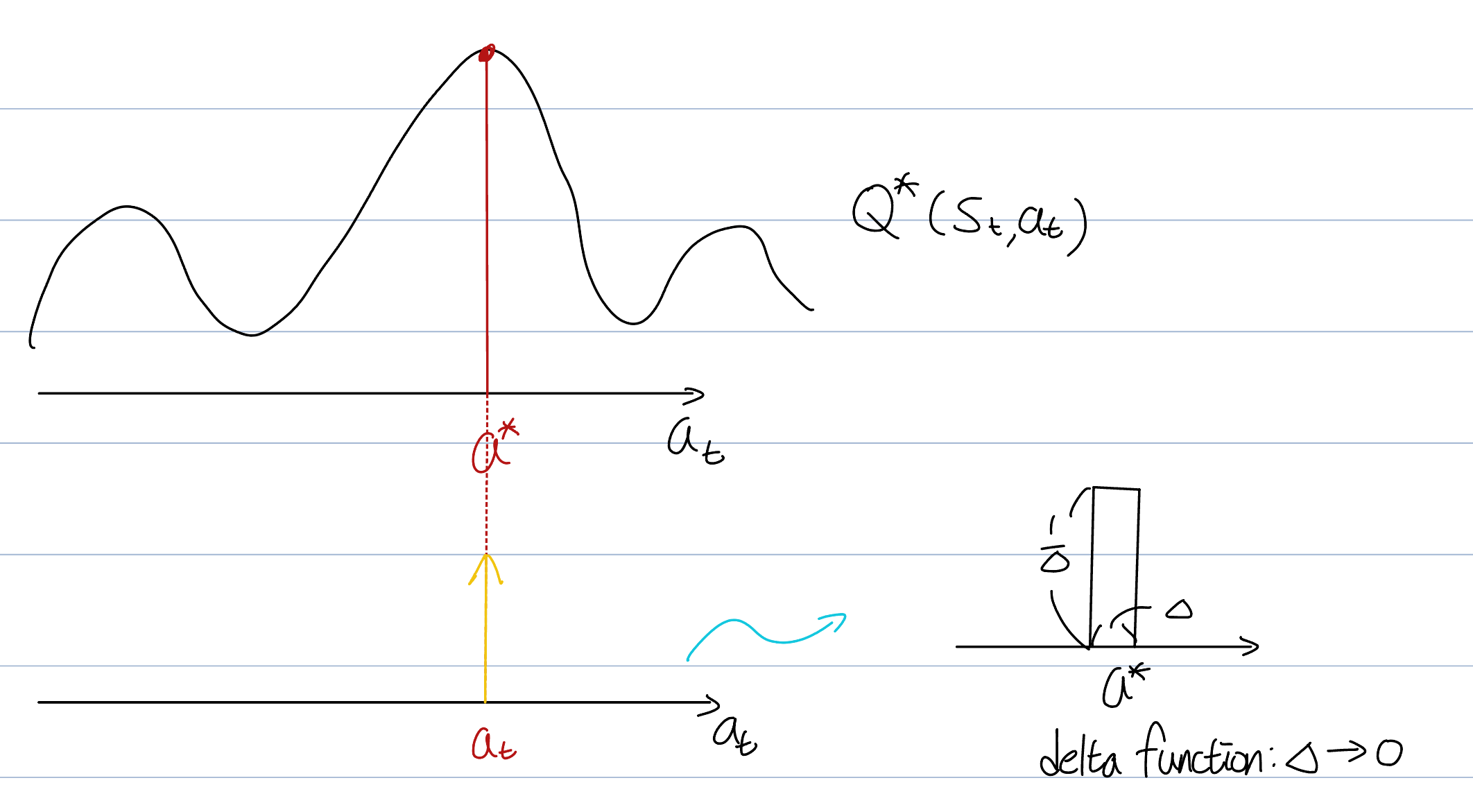
The equation of $a^*$ is:
$a^*=a^*_t \triangleq \argmax\limits_{a_t} Q^*(s_t, a_t)$
And, the distribution becomes:
$p^*(a_t|s_t) = \delta (a_t-a^*_t)$

In short, the policy(probability distribution) is that find the $a^*_t$ maximizing $Q^*$, and integral only with $a^*_t$

We have learned about $\epsilon$-greedy.

Due to the mathematical definition of $Q^*$ in Q-learning, beyond just an intuitive understanding from diagrams, the $\epsilon$-greedy strategy is employed.