Activation function

딥러닝 학습 과정에서 뉴런은 입력 값을 받아 가중치(w)를 곱하고 bias(b)를 더한 후, 활성화 함수를 거쳐 출력 값을 만든다. $wx + b$ 값이 threshold를 넘기면 output을 내고(→ 활성화) threshold보다 작으면 output이 나오지 않게 한다.(→ 비활성화) 이 과정에서 활성화 함수는 신경망에 비선형성을 추가하여 신경망이 복잡한 패턴을 학습하도록 한다.

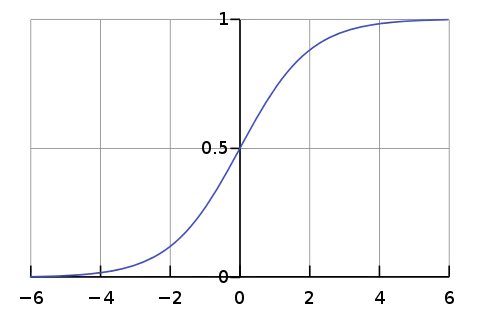
활성화 함수의 종류에는 sigmoid, tanh, ReLU, Leaky ReLU, ELU function 등이 있는데, sigmoid나 tanh는 마지막 레이어를 제외하고는 사실상 거의 쓰이지 않는다.

Sigmoid

$y = \frac{1}{1+e^{-x}}$

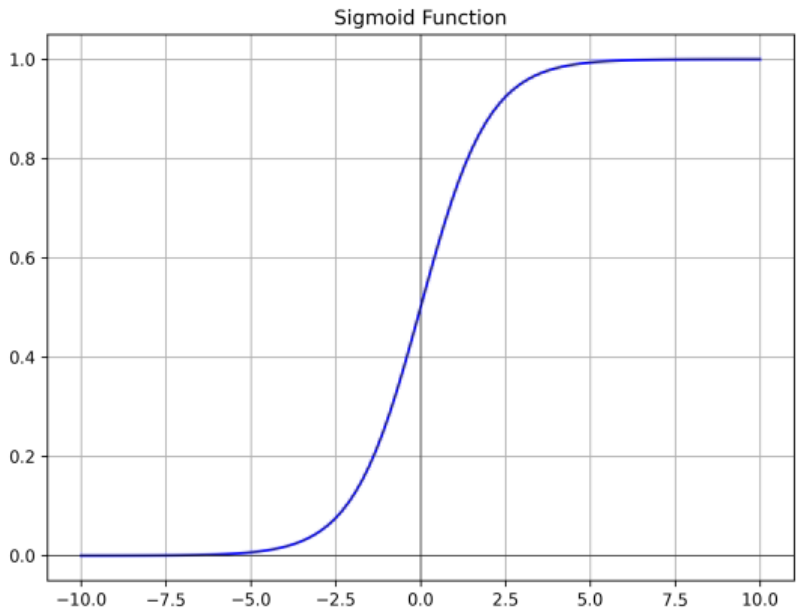
• 출력값이 [0, 1] → 확률로 표현 가능
• input이 크거나 작을 때 기울기가 0에 가까워짐 → backpropagation에서 각종 gradient 값이 0이 됨 → 모델 훈련이 잘 되지 않음
• 출력값들이 zero-centered 하지 않음 (sigmoid function은 x = 0 에서 0.5임) → backpropagation에서 gradient의 부호가 변하지 않아서 특정 방향으로만 업데이트 됨
• exp() 연산이 비쌈

tanh

$y = \frac{e^x - e^{-x}}{e^x + e^{-x}}$

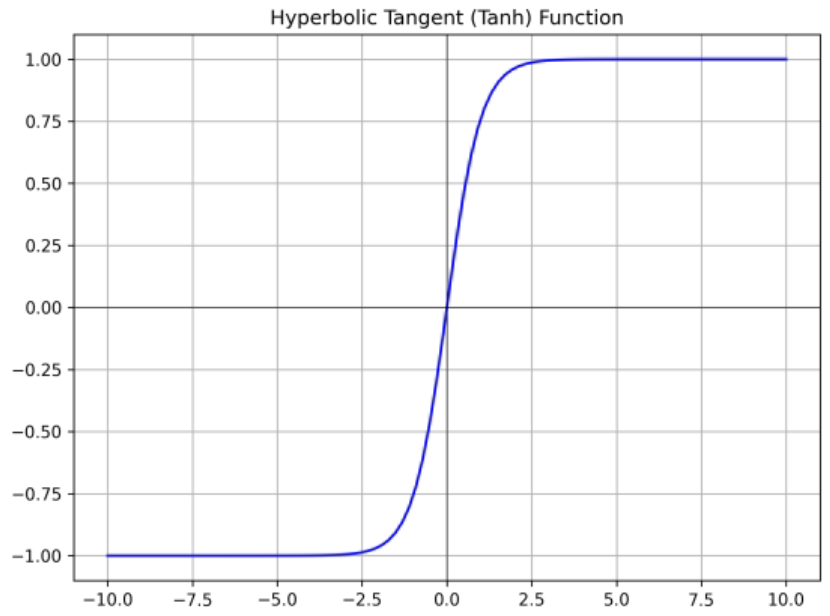
• sigmoid function의 단점을 보완하고자 zero-centered 하게 만듬
• 출력값이 [-1, 1]
• input이 크거나 작을 때 기울기가 0에 가까워지는 문제는 여전히 발생

ReLU

$y = max(0, x)$

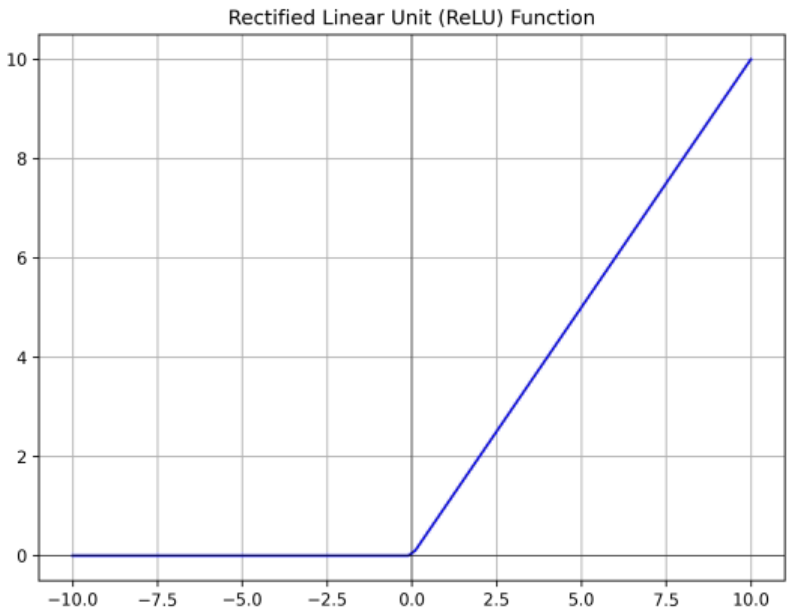
• Rectified Linear Unit
• 양수 영역에서는 기울기가 0이 되지 않음
• 연산이 효율적 (no 미분) → sigmoid나 tanh보다 빠르게 수렴
• 출력값이 zero-centered 되지 않음
• Dead ReLU problem : 음수 영역에서는 output이 다 0
• x = 0 일 때 미분 불가능 → backpropagation을 하기 위해서는 모든 영역에서 미분 가능해야 한다.

Leaky ReLU

$y = max(0.01x, x)$

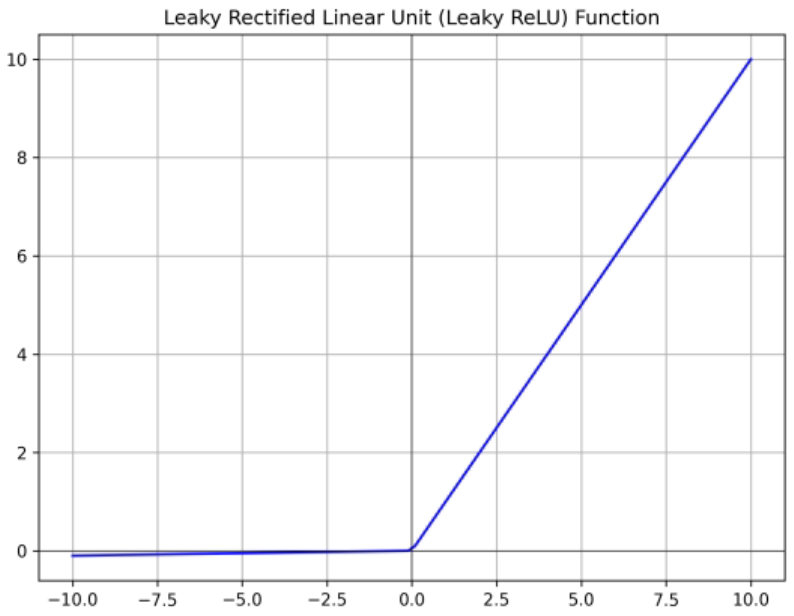
• ReLU의 단점을 보완하기 위함
• 모든 영역에서 기울기가 0이 되지 않음 → No Dead ReLU problem
• 음수인 영역에서 기울기가 생겼기 때문에 hyperparameter가 하나 늘어난 셈.

ELU

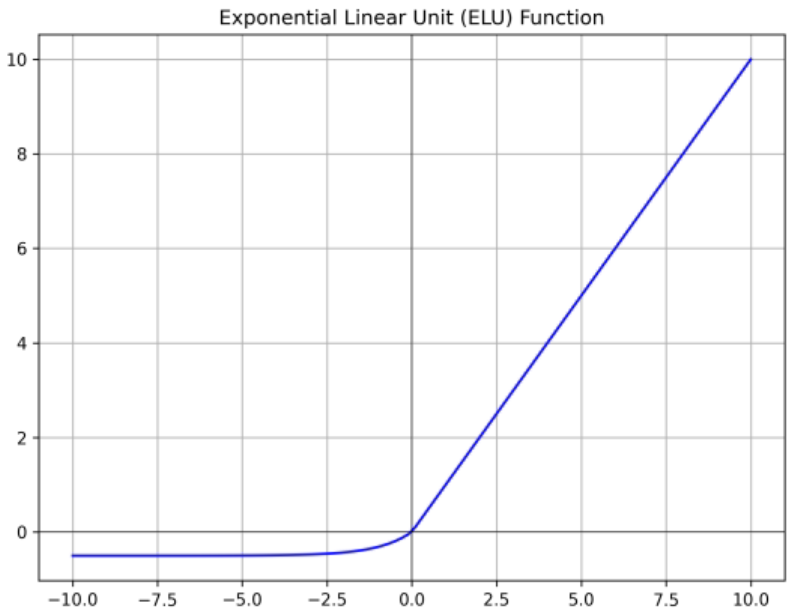
$y = x$ if $x \geq 0$
$y = \alpha (e^x - 1)$ if $x \lt 0$

• Exponential Linear Unit
• ReLU의 모든 장점을 갖춤
• exp() 연산이 비쌈

Softmax

$f(x_i) = \frac{e^{x_i}}{\sum_j e^{x_j}}$
where $x_i$ = i번째 클래스의 입력 값 (logit 값)

다중 클래스 분류에서 사용하는, 특히 마지막 층의 활성화 함수이다. 신경망의 마지막 층에서 출력되는 logit 값은 그대로 확률로 해석하기 어렵기 때문에 softmax를 적용하여 각 클래스로 분류될 확률로 변환한다.

예를 들어 3개의 클래스를 분류하는 모델이 있고, 마지막 층에서 나온 logit 값이 x = [2.0, 1.0, 0.1]이라고 하자. 그러면 먼저 이 logit 값에 지수 함수를 적용하여 $e^x$ = [$e^{2.0}$, $e^{1.0}$, $e^{0.1}$] = [7.389, 2,718, 1.105]가 된다. 그래서 결과적으로

$P(클래스 1) = \frac{7.389}{7.389+2.718+1.105} = 0.659$
$P(클래스 2) = \frac{2.718}{7.389+2.718+1.105} = 0.242$
$P(클래스 3) = \frac{1.105}{7.389+2.718+1.105} = 0.099$

와 같이 계산되어 65.9% 확률로 클래스 1로 분류되는 것이다.

요약

	출력 범위	특징	장점	단점	주로 사용되는 곳
Sigmoid	(0, 1)	S자 곡선	확률 값 표현	기울기 소실	이진 분류의 마지막 층
Tanh	(-1, 1)	S자 곡선	0 중심	기울기 소실	RNN
ReLU	[0, $\infty$)	0 또는 입력 값	학습 빠름	죽은 뉴런 문제	CNN, MLP
Leaky ReLU	(-$\infty$, $\infty$)	작은 기울기 유지	죽은 뉴런 문제 해결	하이퍼 파라미터 필요	대체 ReLU
Softmax	(0, 1)	확률 분포	다중 분류 가능	계산량 많음	다중 분류의 마지막 층