🌿 합성곱 신경망
Convolutional neural network, CNN
CNN의 네트워크 구조
- 계층을 조합하여 CNN을 만듦
- 합성곱 계층(convolutional layer)과 풀링 계층(pooling layer)이 등장
완전연결 계층(Affine 계층)으로 이루어진 네트워크의 예
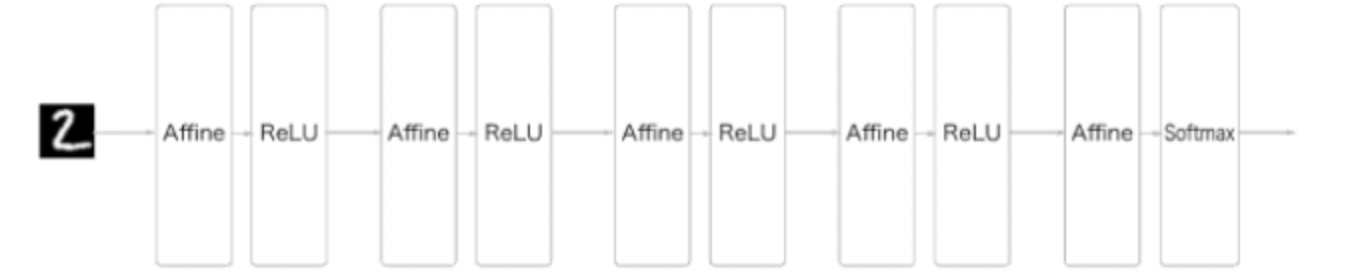
CNN으로 이루어진 네트워크의 예

일반적인 CNN의 구성
- Affine-ReLU 연결이 Conv-ReLU-(Pooling)의 형태로 바뀜
- 출력에 가까운 층에서는 Affine-ReLU 구성을 사용할 수 있음
- 마지막 출력 계층에서는 Affine-Softmax 조합을 그대로 사용
합성곱 계층
패딩(Padding), 스트라이드(stride) 등의 CNN 고유 용어 등장
각 계층 사이에 3차원 데이터와 같이 입체적 데이터가 흐른다는 점에서 완전연결 신경망과 다름
🚨 완전연결 계층의 문제
데이터의 형상이 무시된다는 문제점
MNIST 데이터도 완전연결 계층을 이용할 때 1차원 데이터로 평탄화하는 작업을 거침
→ 공간적 정보의 손실 발생 가능
공간적 정보의 예시
- 공간적으로 가까운 픽셀의 값이 비슷한 경우
- RGB의 각 채널의 관련성
- 거리가 먼 픽셀끼리는 연관이 줄어든다는 점
- 3차원 속에서 의미를 갖는 본질적 패턴
합성곱 계층은 형상을 유지함으로써 '형상을 가진 데이터'를 제대로 이해할 가능성을 높임
⌗ 합성곱 연산
합성곱 연산은 이미지 처리에서 말하는 필터 연산에 해당
예시는 다음과 같다.
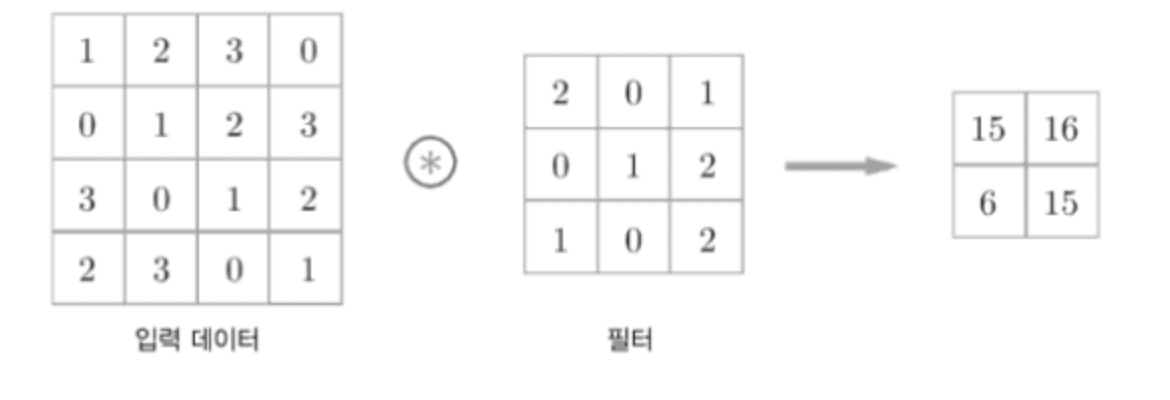
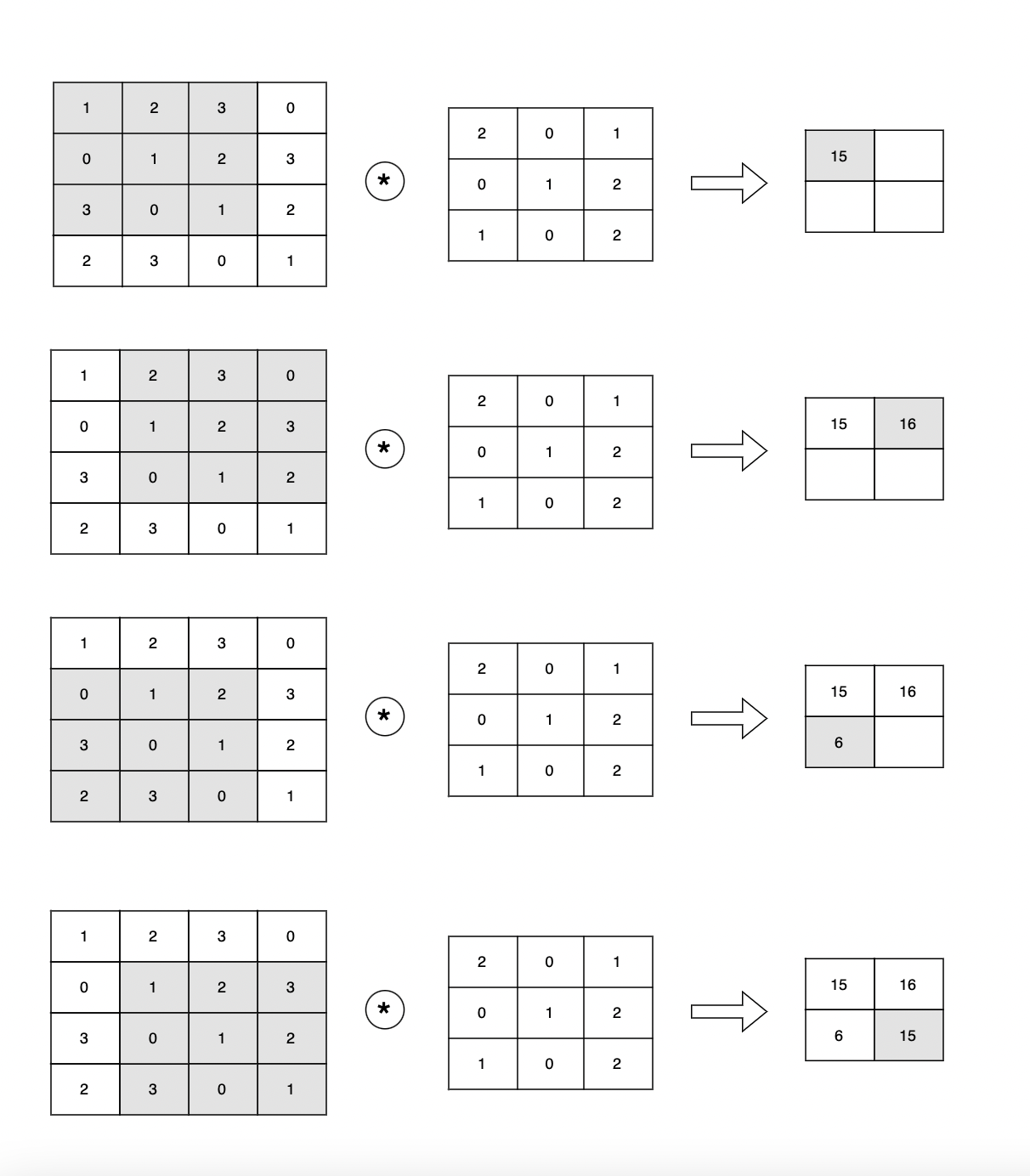
합성곱 연산은 필터의 윈도우(window)를 일정 간격으로 이동해가며 입력 데이터에 적용
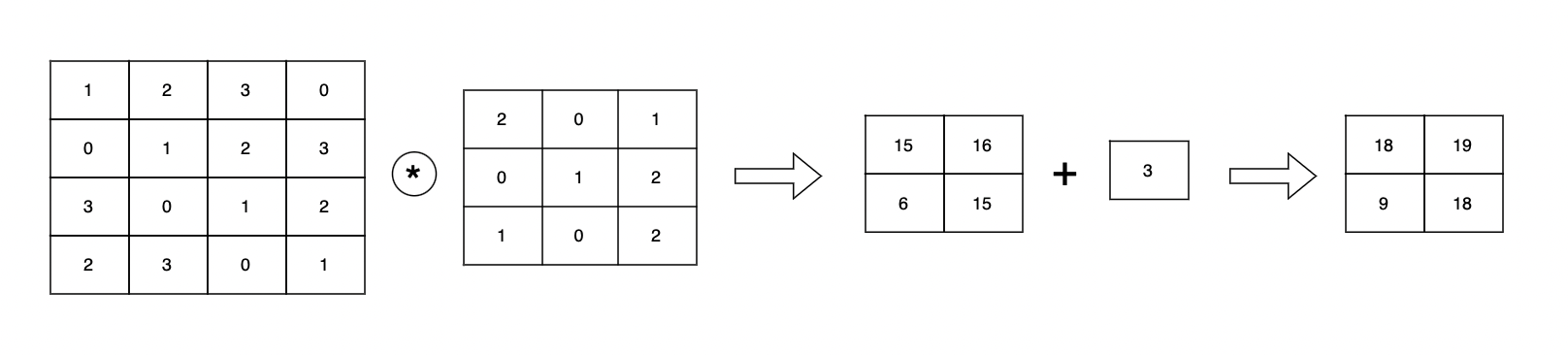
입력 데이터와 필터가 대응하는 원소끼리 곱한 후 그 총합을 구한다 (단일 곱셈-누산 fused multiply-add, FMA)
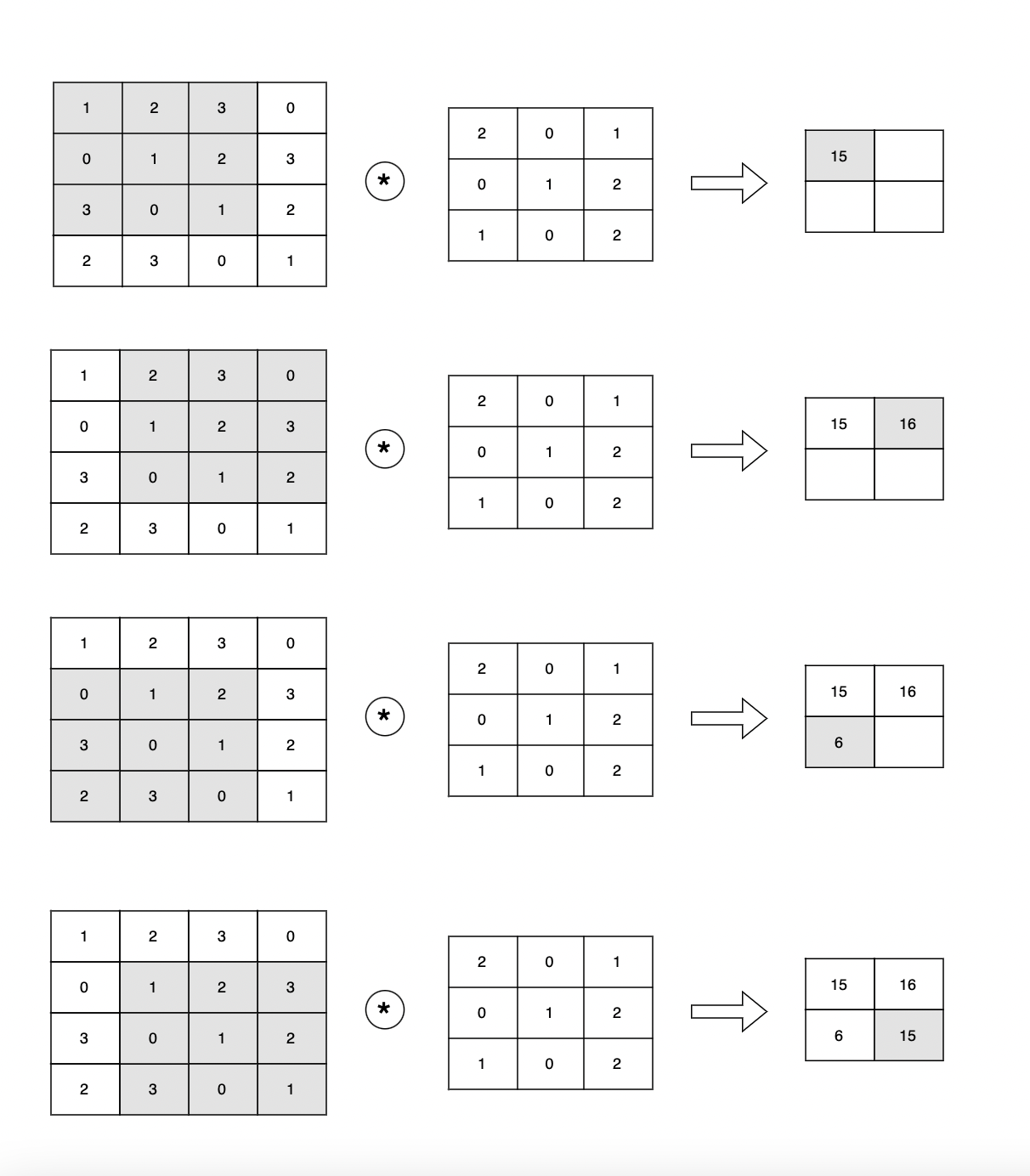
CNN에서는 필터의 매개변수가 그동안의 '가중치'에 해당
편향까지 포함하면 다음과 같다.
📍 패딩(padding)
합성곱 연산을 수행하기 전 입력 데이터 주변을 특정 값(ex. 0)으로 채우는 것을 패딩이라고 함
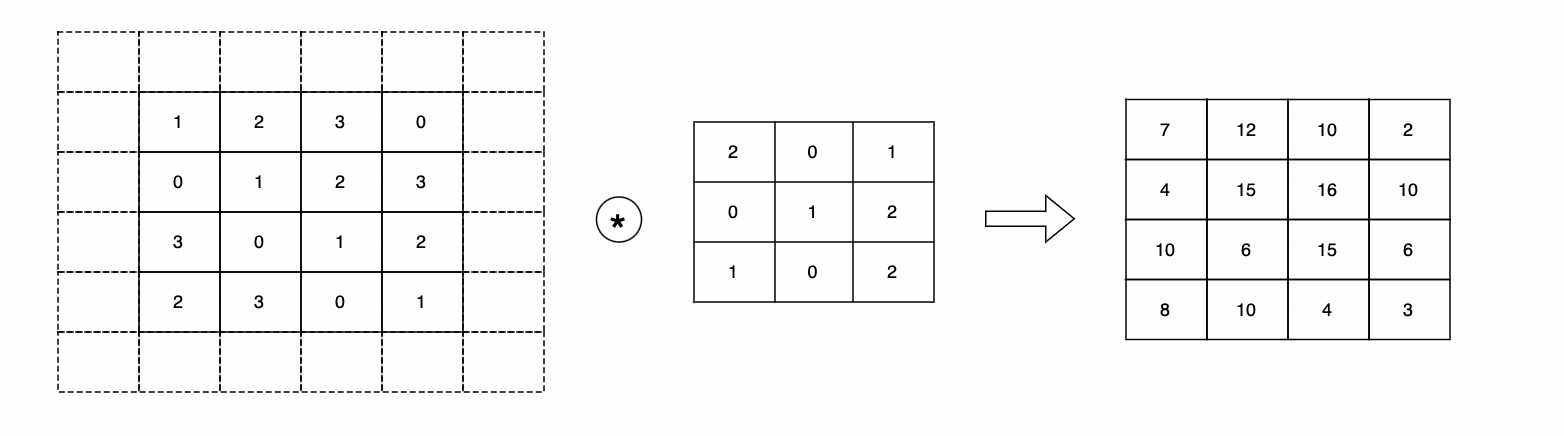
입력 데이터(4,4)에 패딩을 추가하여 (6,6)으로 만듦
이 입력에 (3,3) 필터를 걸면 (4,4) 크기의 출력 데이터 생성
패딩은 주로 출력 크기를 조정할 목적으로 사용
ex) (4,4) 입력 데이터에 (3,3) 필터 → (2,2) 출력 데이터
위와 같은 예시에서는 출력 데이터가 입력보다 2만큼 줄어든다.
합성곱을 되풀이하는 심층 신경망에서 출력의 크기가 작아지는 것을 막고 공간적 크기를 고정하여 다음 계층으로 전달할 수 있게 함
📍 스트라이드(stride)
필터를 적용하는 위치의 간격을 스트라이드라고 함
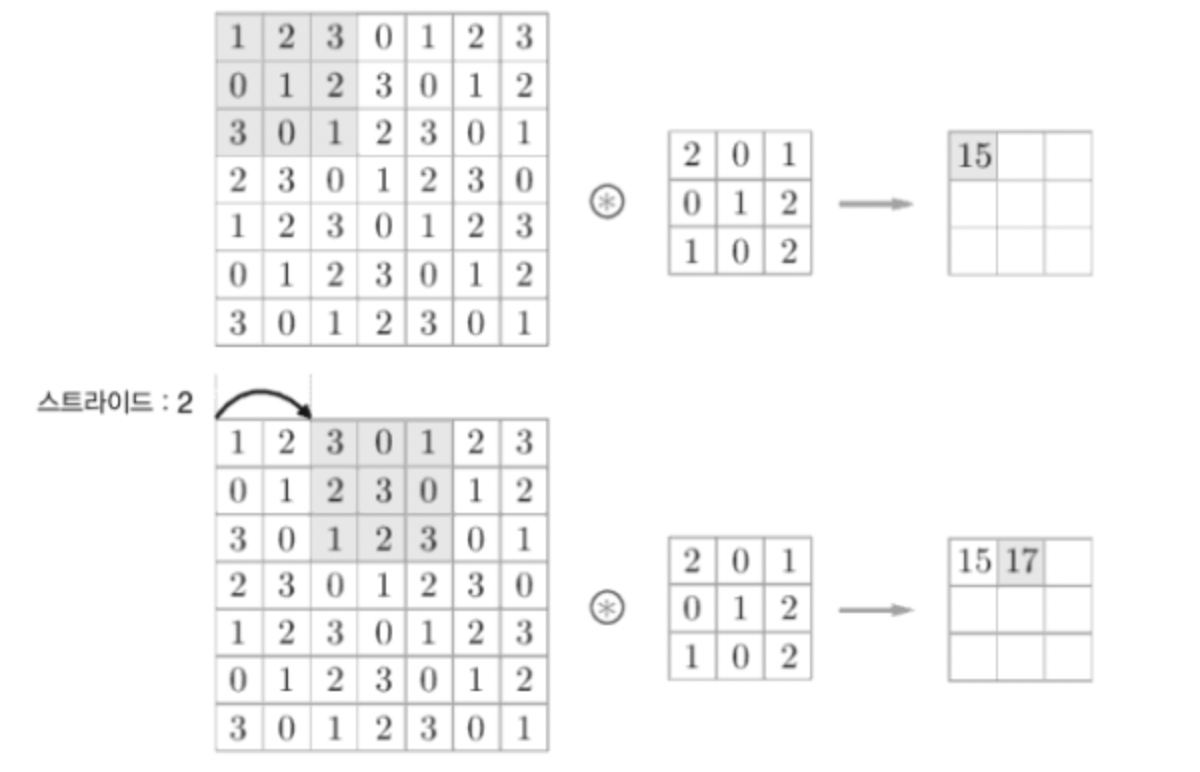
스트라이드를 키울수록 출력의 크기는 작아지게 됨
패딩과 스트라이드의 크기에 따른 출력 데이터의 크기를 수식화하면 다음과 같다.
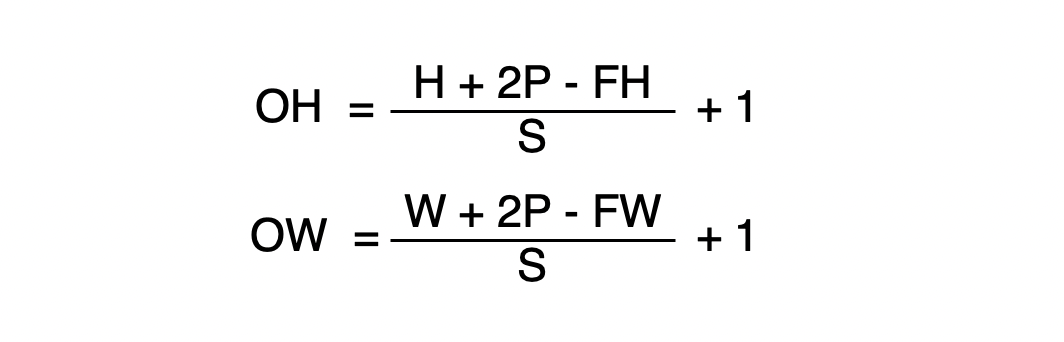
입력 크기 : (H, W)
필터 크기 : (FH, FW)
출력 크기 : (OH, OW)
패딩 : P
스트라이드 : S
** 단 (H+2P-FH)/S 와 (W+2P-FW)/S의 값이 정수로 나눠떨어지는 값이어야 함
3차원 데이터의 합성곱 연산
2차원일 때와 비교하면 길이 방향(채널 방향)으로 특징 맵이 늘어남
입력 데이터와 필터의 합성곱 연산을 채널마다 수행 하고 그 결과를 더해 하나의 출력을 얻음
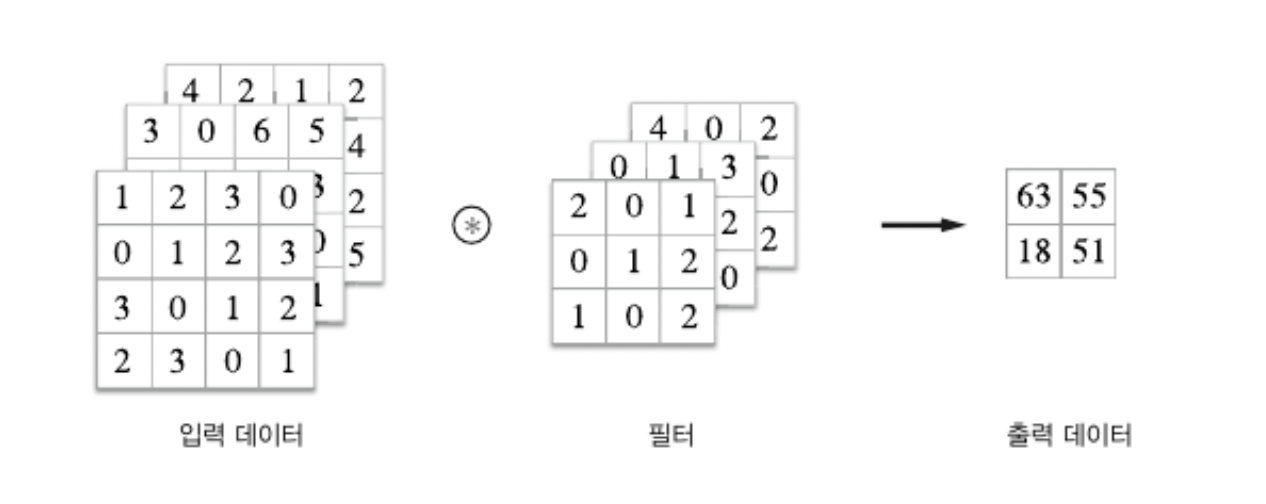
계산 순서는 다음과 같다.
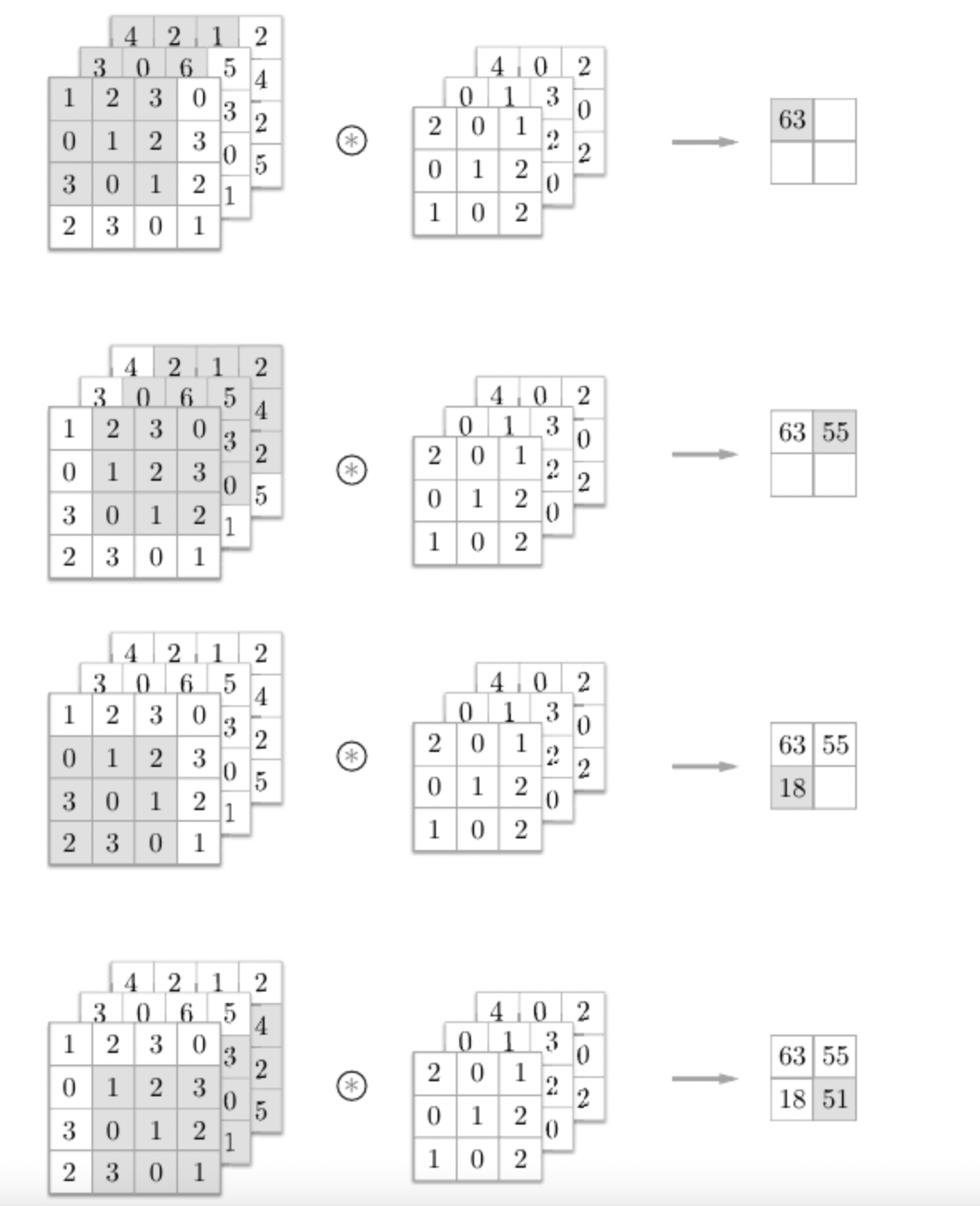
🧱 블록으로 생각하기
3차원 합성곱 연산은 데이터와 필터를 직육면체 블록이라고 생각할 수 있다.
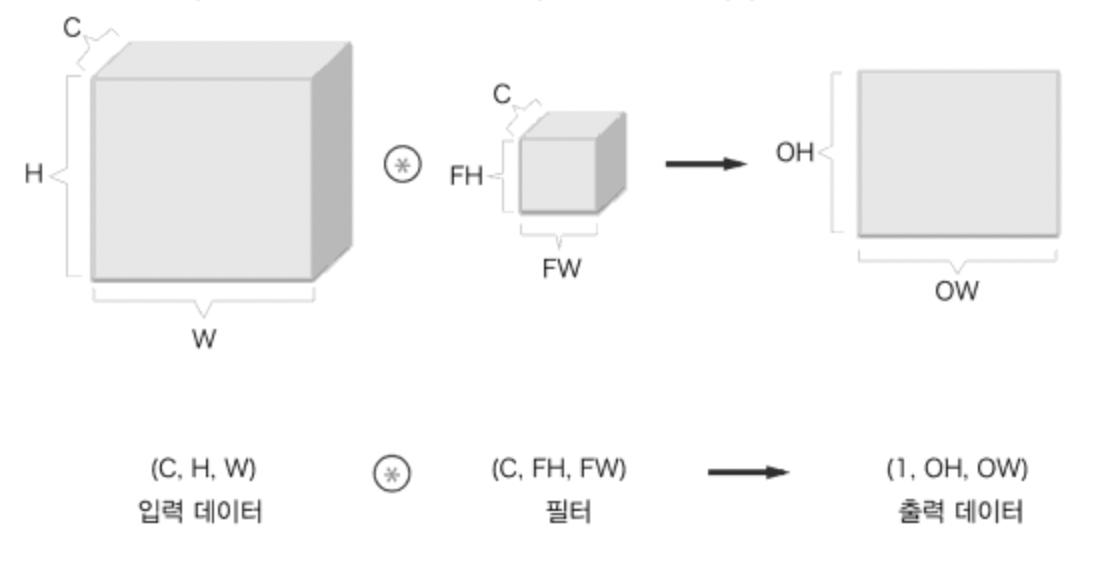
위와 같이 출력 데이터는 한 장의 특징 맵 (채널이 1개인 특징 맵)이 된다.
합성곱 연산의 출력으로 다수의 채널을 내보내기 위해서는 필터(가중치)를 다수 사용해야 함
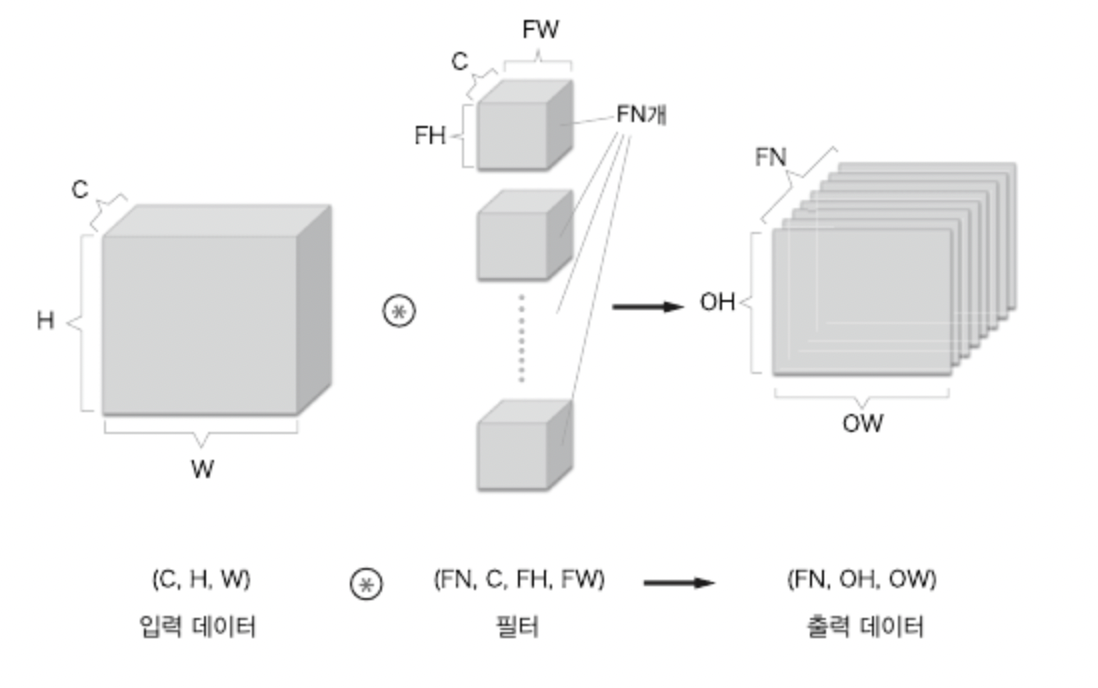
편향까지 추가하면 다음과 같다.
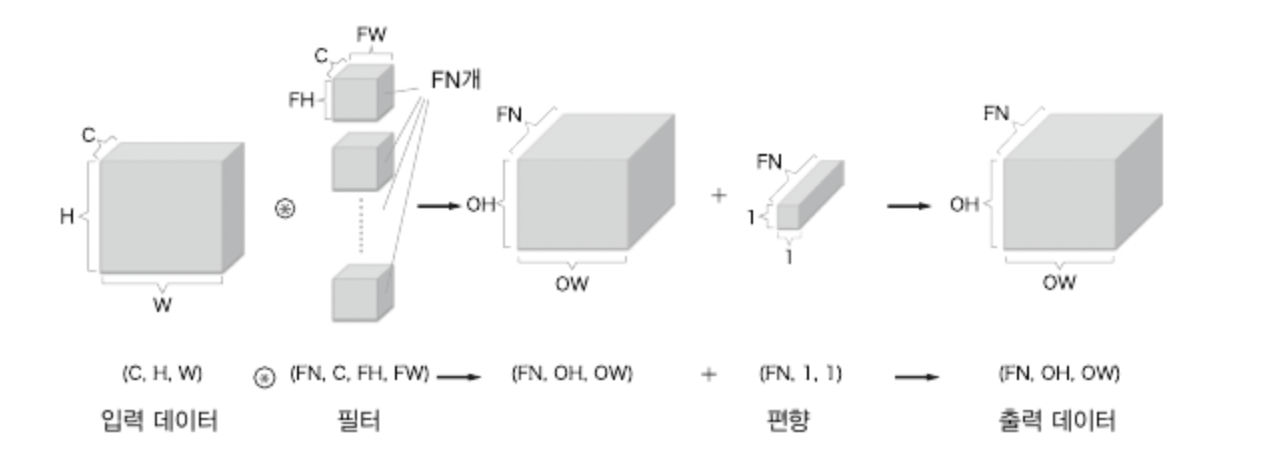
배치 처리
합성곱 연산에서 각 계층을 흐르는 데이터의 차원을 하나 늘려 4차원 데이터로 저장함으로써 배치 처리를 지원할 수 있다.
데이터가 N개일 때 배치 처리를 하면 다음과 같이 진행된다.
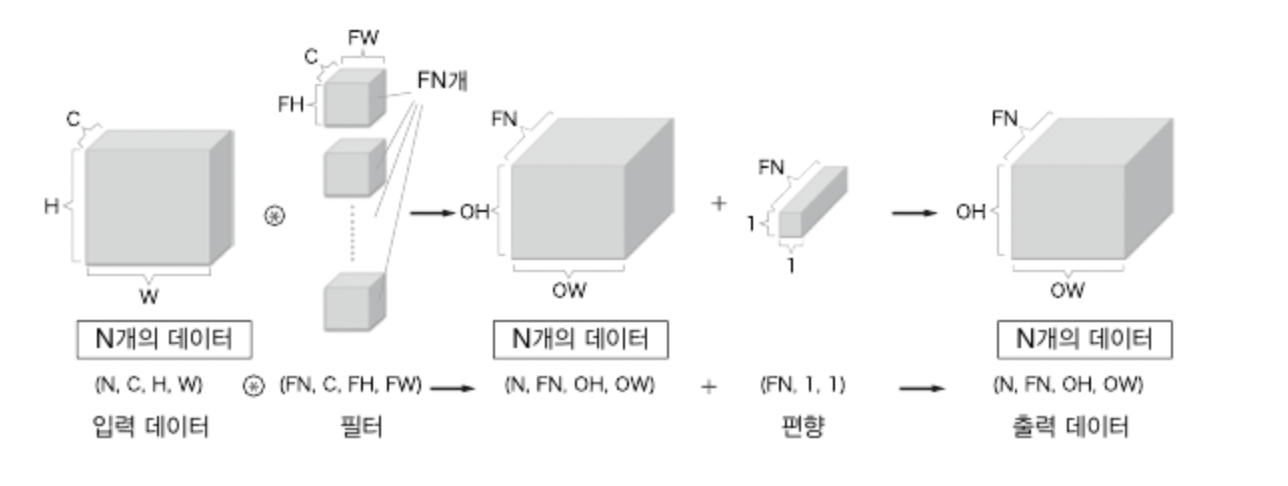
신경망에 4차원 데이터가 하나 흐를 때마다 데이터 N개에 대한 합성곱 연산이 처리됨
