🌿 풀링 계층
풀링은 세로·가로 방향의 공간을 줄이는 연산
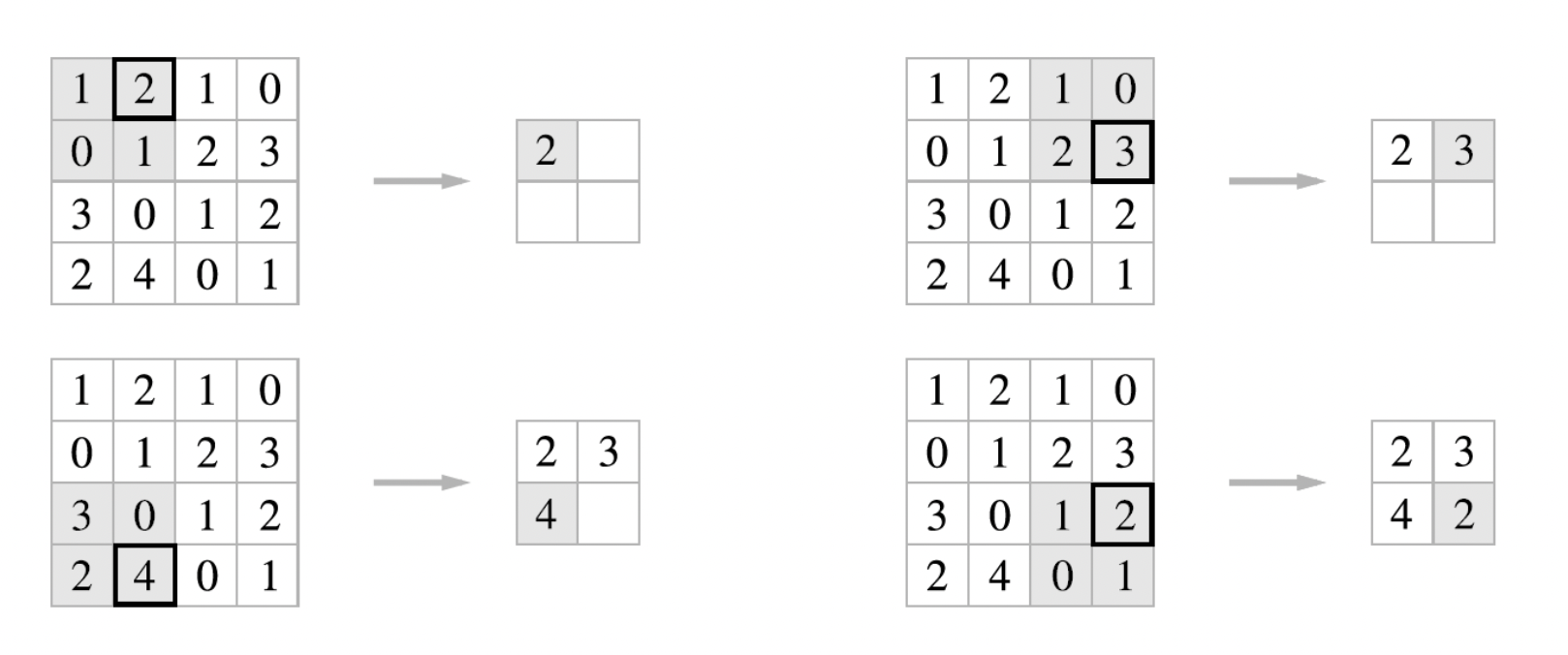
2x2 최대 풀링(max pooling) 을 스트라이드 2로 처리하는 순서는 다음과 같다.
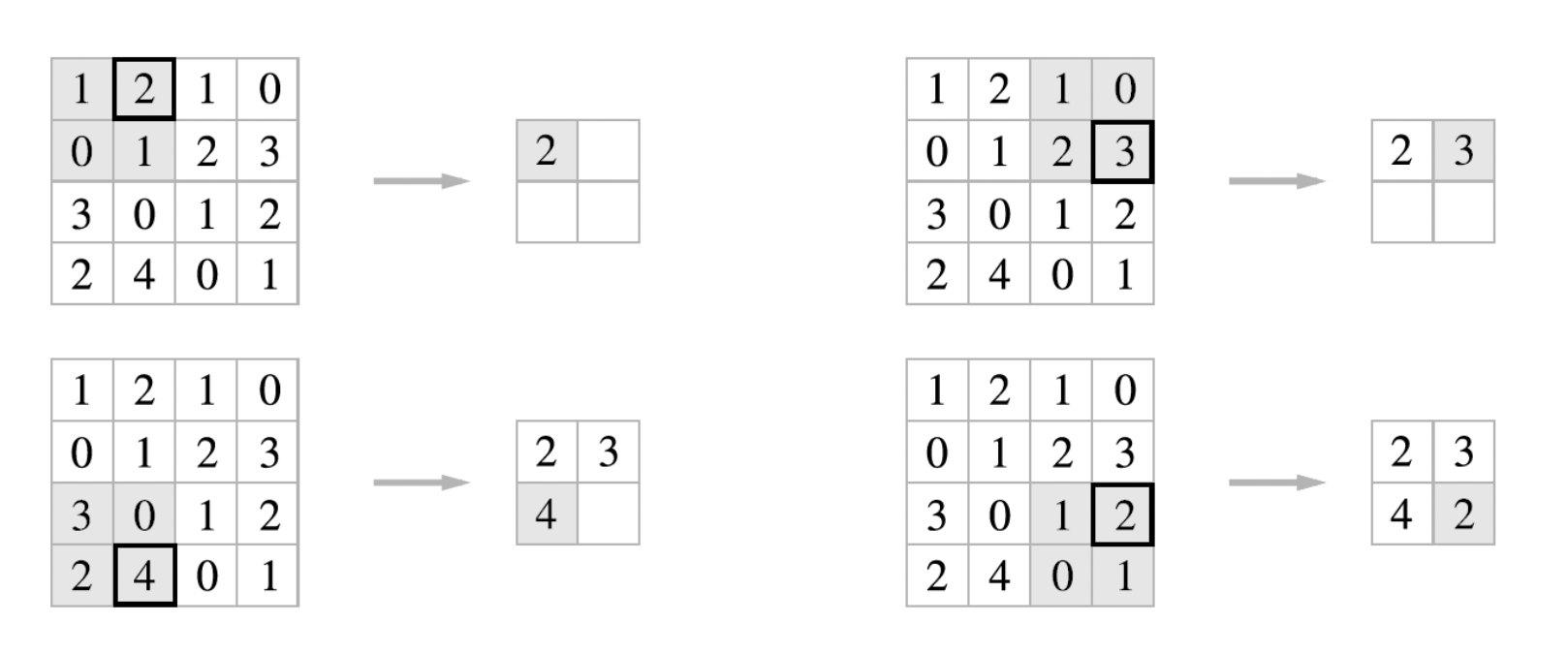최대 풀링은 최댓값을 구하는 연산
2x2는 대상 영역의 크기를 의미, 즉 2x2 크기의 영역에서 가장 큰 원소를 하나씩 꺼냄
주로 풀링의 윈도우 크기와 스트라이드는 같은 값으로 설정
풀링 계층의 특징
- 학습해야 할 매개변수가 없다
대상 영역에서 최댓값이나 평균을 취하는 명확한 처리이므로 별도의 학습이 필요하지 않음
- 채널 수가 변하지 않는다
채널마다 독립적으로 계산하므로 입력 데이터의 채널 수 그대로 출력 데이터로 보냄
- 입력 변화에 영향을 적게 받는다
입력 데이터가 변해도 풀링의 결과는 잘 변하지 않음
👩🏻💻 합성곱/풀링 계층의 구현
CNN에서 계층 사이를 흐르는 데이터는 4차원
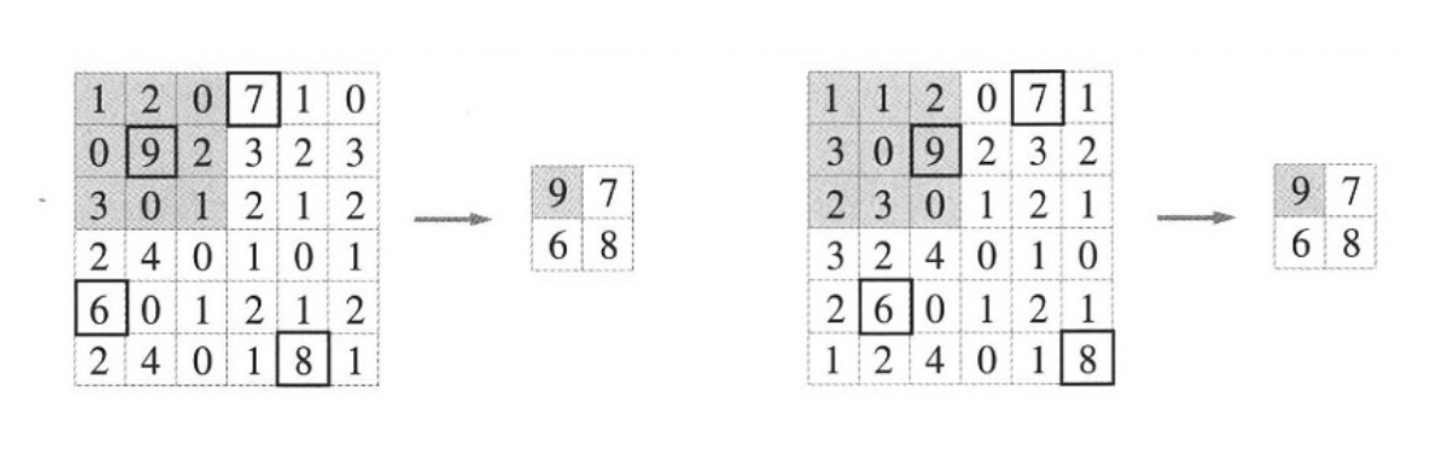
이를 im2col로 데이터 전개하여 구현할 수 있다.
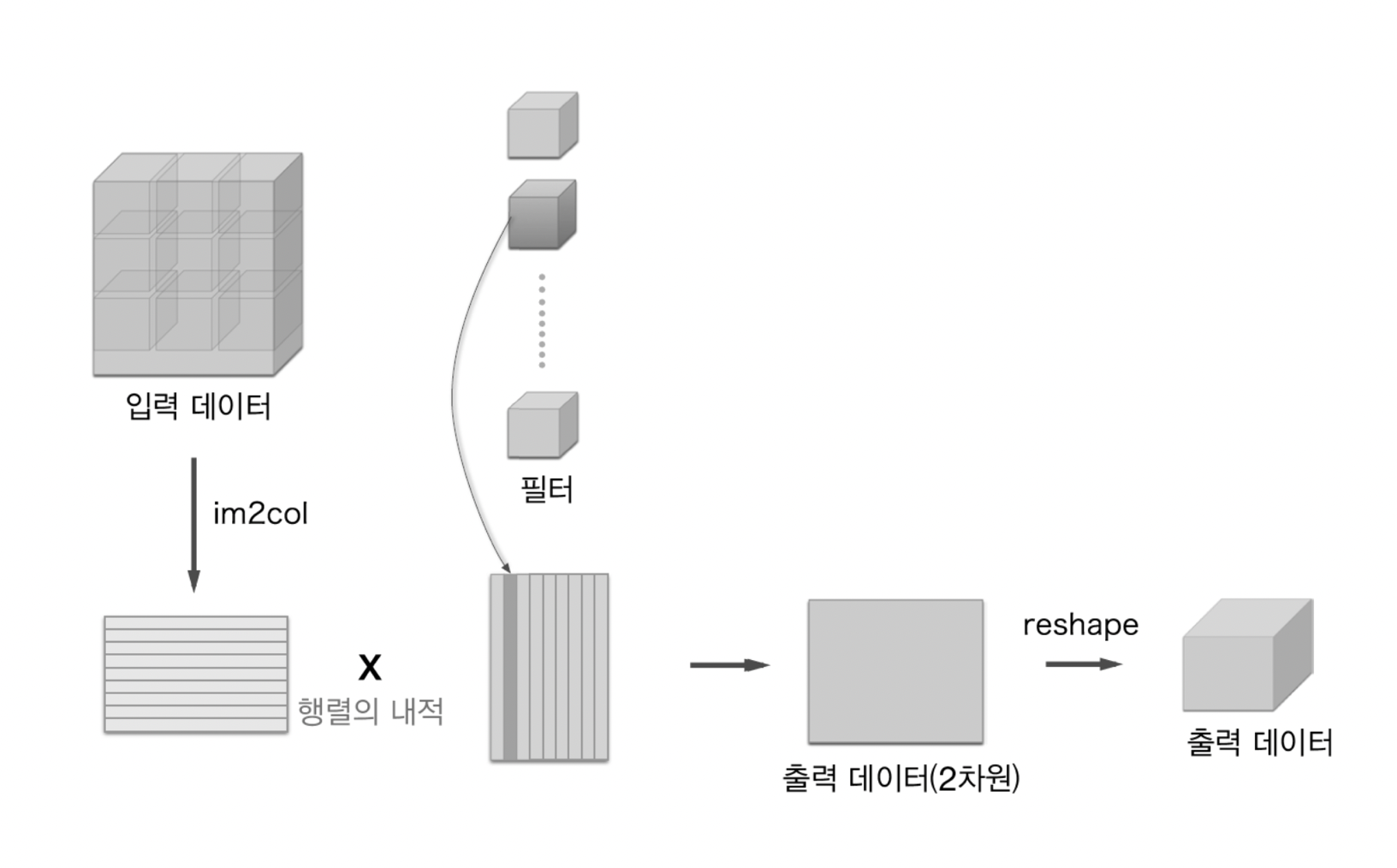
im2col로 데이터 전개하기
im2col은 입력 데이터를 필터링(가중치 계산)하기 좋게 전개하는 함수
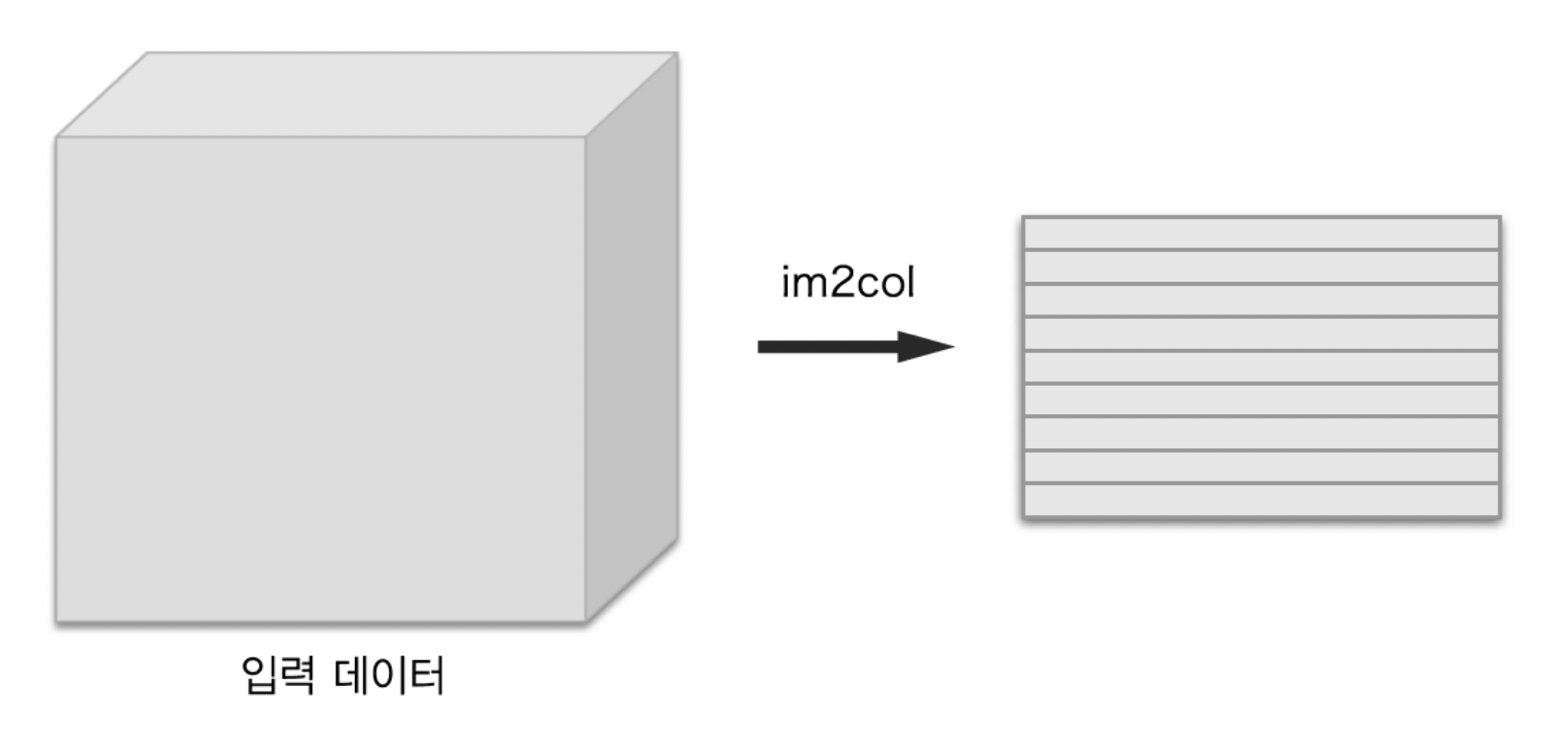
위와 같이 im2col을 통해 3차원 입력 데이터를 2차원 행렬로 바꿀 수 있음
정확히는 배치 안의 데이터 수까지 4차원 데이터를 2차원으로 변환
합성곱 연산은 이를 활용하여 다음과 같이 진행이 가능하다.
- 필터 적용 영역을 앞에서부터 순서대로 1줄로 변환
- 필터를 세로로 1열로 전개한 뒤 두 데이터의 행렬 곱을 계산
- 최종 결과를 reshape하여 형상 복구
im2col의 구현은 다음과 같다.
def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
"""다수의 이미지를 입력받아 2차원 배열로 변환한다(평탄화).
Parameters
----------
input_data : 4차원 배열 형태의 입력 데이터(이미지 수, 채널 수, 높이, 너비)
filter_h : 필터의 높이
filter_w : 필터의 너비
stride : 스트라이드
pad : 패딩
Returns
-------
col : 2차원 배열
"""
N, C, H, W = input_data.shape
out_h = (H + 2*pad - filter_h)//stride + 1
out_w = (W + 2*pad - filter_w)//stride + 1
img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant')
col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))
for y in range(filter_h):
y_max = y + stride*out_h
for x in range(filter_w):
x_max = x + stride*out_w
col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]
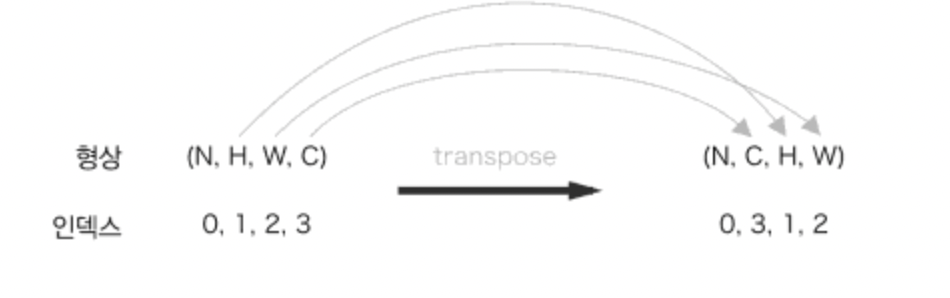
col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N*out_h*out_w, -1)
return col합성곱 계층의 구현
im2col은 다음과 같이 사용이 가능하다.
이를 활용하여 합성곱 계층을 Convolution이라는 클래스로 구현하자.
class Convolution:
def __init__(self, W, b, stride=1, pad=0):
self.W = W
self.b = b
self.stride = stride
self.pad = pad
def forward(self, x):
FN, C, FH, FW = self.W.shape
N, C, H, W = x.shape # 입력
out_h = int(1 + (H + 2*self.pad - FH) / self.stride)
out_w = int(1 + (W + 2*self.pad - FW) / self.stride)
col = im2col(x, FH, FW, self.stride, self.pad)
col_W = self.W.reshape(FN, -1).T # 필터의 전개 (세로)
out = np.dot(col, col_W) + self.b
out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2) # 출력데이터를 적절한 형상으로 복구transpose 함수는 다차원 배열의 축 순서를 바꿔주는 함수이다.
풀링 계층의 구현
풀링 계층도 합성곱 계층처럼 im2col을 사용해 입력 데이터를 전개
풀링의 경우 채널 쪽이 독립적이므로 채널마다 독립적으로 전개
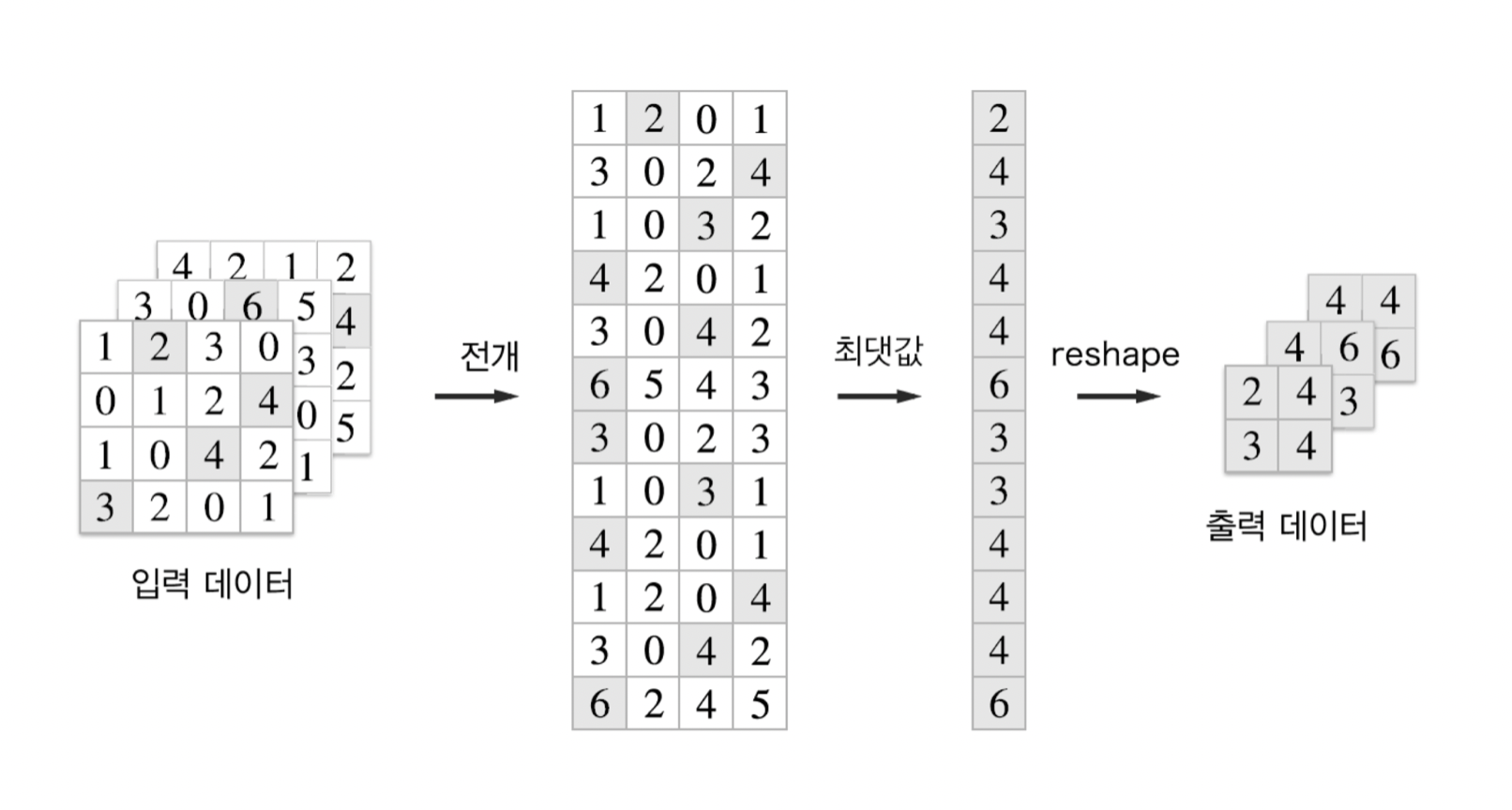
- 전개 후 pooling 사이즈에 맞게 reshape
- 각 행마다 최댓값을 추출 (max pooling)
- 적절한 형상으로 다시 reshape
코드는 다음과 같이 구현이 가능하다.
class Pooling:
def __init__(self, pool_h, pool_w, stride=1, pad=0):
self.pool_h = pool_h
self.pool_w = pool_w
self.stride = stride
self.pad = pad
def forward(self, x):
N, C, H, W = x.shape
out_h = int(1 + (H - self.pool_h) / self.stride)
out_w = int(1 + (W - self.pool_w) / self.stride)
# 전개 (1)
col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
col = col.reshape(-1, self.pool_h*self.pool_w) # pooling의 사이즈를 열의 크기로 reshape
# 최댓값 (2)
out = np.max(col, axis=1)
# 성형 (3)
out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)
return outCNN의 구현
아래의 단순한 CNN 네트워크를 SimpleConvNet이라는 클래스로 구현해보자
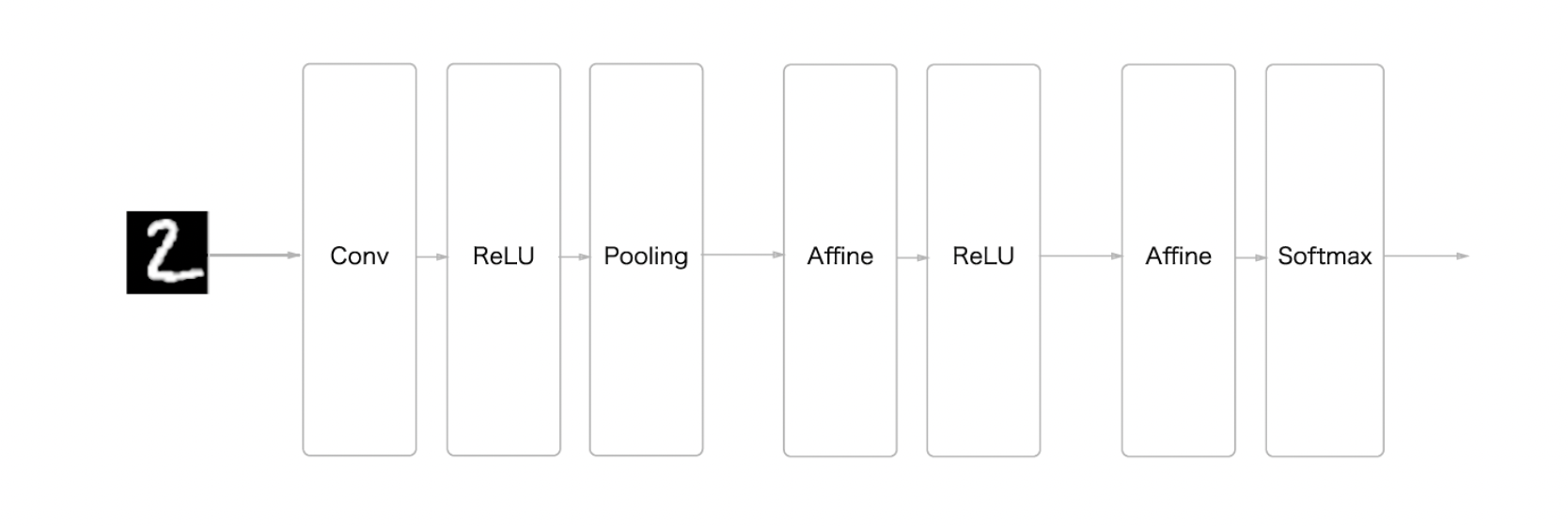
초기화 인수
- input_dim : 입력 데이터 (채널 수, 높이, 너비)
- conv_param : 합성곱 계층의 하이퍼파라미터(딕셔너리)
- filter_num - 필터 수
- filter_size - 필터 크기
- stride - 스트라이드
- pad - 패딩
- hidden_size - 은닉층(완전연결)의 뉴런 수
- output_size - 출력층(완전연결)의 뉴런 수
- weight_init_std - 초기화 때의 가중치 표준편차
class SimpleConvNet:
def __init__(self, input_dim=(1, 28, 28),
conv_param={'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1},
hidden_size=100, output_size=10, weight_init_std=0.01):
filter_num = conv_param['filter_num']
filter_size = conv_param['filter_size']
filter_pad = conv_param['pad']
filter_stride = conv_param['stride']
input_size = input_dim[1]
# 현재 filter로 합성곱 계층을 거쳤을 때 출력 데이터 크기
conv_output_size = (input_size - filter_size + 2*filter_pad) / filter_stride + 1
# 현재 filter로 풀링 계층을 거쳤을 때 출력 데이터 크기
pool_output_size = int(filter_num * (conv_output_size/2) * (conv_output_size/2))
self.params = {}
self.params['W1'] = weight_init_std * np.random.rand(filter_num, input_dim[0], filter_size, filter_size)
self.params['b1'] = np.zeros(filter_num)
self.params['W2'] = weight_init_std * np.random.randn(pool_output_size, hidden_size)
self.params['b2'] = np.zeros(hidden_size)
self.params['W3'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b3'] = np.zeros(output_size)
self.layers = OrderedDict()
self.layers['Conv1'] = Convolution(self.params['W1'], self.params['b1'], conv_param['stride'], conv_param['pad'])
self.layers['Relu1'] = Relu()
self.layers['Pool1'] = Pooling(pool_h=2, pool_w=2, stride=2)
self.layers['Affine1'] = Affine(self.params['W2'], self.params['b2'])
self.layers['Relu2'] = Relu()
self.layters['Affine2'] = Affine(self.params['W3'], self.params['b3'])
self.last_layer = SoftmaxWithLoss()
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
def loss(self, x, t):
y = self.predict(x)
return self.last_layer.forward(y, t)
def gradient(self, x, t):
# 순전파
self.loss(x, t)
# 역전파
dout = 1
dout = self.last_layer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 결과 저장
grads = {}
grads['W1'] = self.layers['Conv1'].dW
grads['b1'] = self.layers['Conv1'].db
grads['W2'] = self.layers['Affine1'].dW
grads['b2'] = self.layers['Affine1'].db
grads['W3'] = self.layers['Affine2'].dW
grads['b3'] = self.layers['Affine2'].db
return grads각 계층의 순전파와 역전파 기능을 잘 구현했다면 이를 적절한 순서로 호출함으로써 CNN을 구현할 수 있다.
CNN의 시각화
1번째 층의 가중치 시각화
MNIST 데이터셋에 대하여 1번째 층의 합성곱 계층 형상을 (30, 1, 5, 5)로 두자.
이는 필터의 크기가 5x5이고 채널이 1개이므로 회색조 이미지로 시각화할 수 있음을 의미한다.
학습 전 필터는 무작위로 초기화되어 있어 흑백의 정도에 규칙성이 없으나
학습을 마친 필터는 규칙성 있는 이미지가 되었음
이 규칙성 있는 필터는 에지(색상이 바뀌는 경계)와 블롭(국소적으로 덩어리진 영역)을 보고 있음
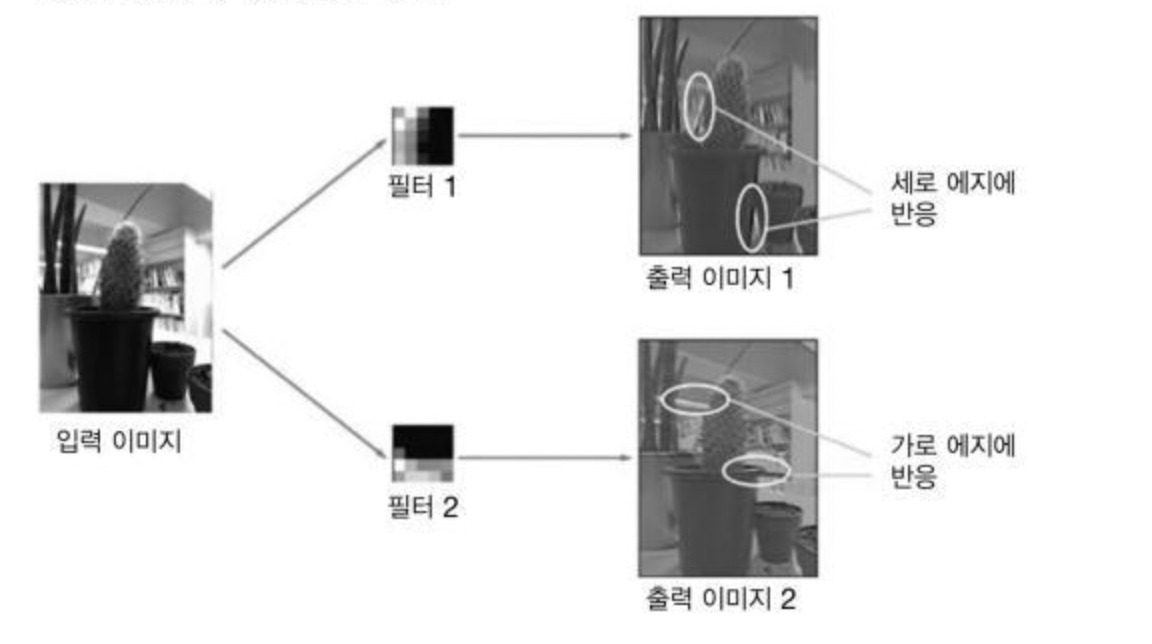
이처럼 합성곱 계층의 필터는 에지나 블롭 등의 원시적 정보를 추출할 수 있다.
이런 원시적 정보를 뒷단 계층에 전달하는 것이 CNN에서 일어나는 일 !
층 깊이에 따른 추출 정보 변화
딥러닝 시각화에 관한 연구에 따르면 계층이 깊어질수록 추출되는 정보(강하게 반응하는 뉴런)이 더 추상화된다고 한다.
1번째 층은 에지와 블롭, 3번째 층은 텍스처, 5번째 층은 사물의 일부, 마지막 완전연결 계층은 사물의 클래스(개, 자동차 등)에 뉴런이 반응하고 있다.
층이 깊어지면서 뉴런이 반응하는 대상이 단순한 모양에서 '고급' 정보로 변화함을 알 수 있다.
즉, 사물의 '의미'를 이해하도록 변화한다.
대표적인 CNN
📍 LeNet (1998)
- CNN의 원조
- 손글씨 숫자를 인식하는 네트워크
- 합성곱 계층과 풀링 계층(단순히 '원소를 줄이기'만 하는 서브샘플링 계층)을 반복하고, 마지막으로 완전연결 계층을 거쳐 결과 출력
현재 CNN과 LeNet의 차이
- 활성화 함수
LeNet은 시그모이드 함수를 사용, 현재는 ReLU를 주로 사용- 풀링 계층
LeNet은 서브샘플링하여 중간 데이터의 크기를 줄이기만 함
현재는 최대 풀링이 주류
📍 AlexNet (2012)
딥러닝 열풍을 일으키는데 큰 역할을 한 네트워크
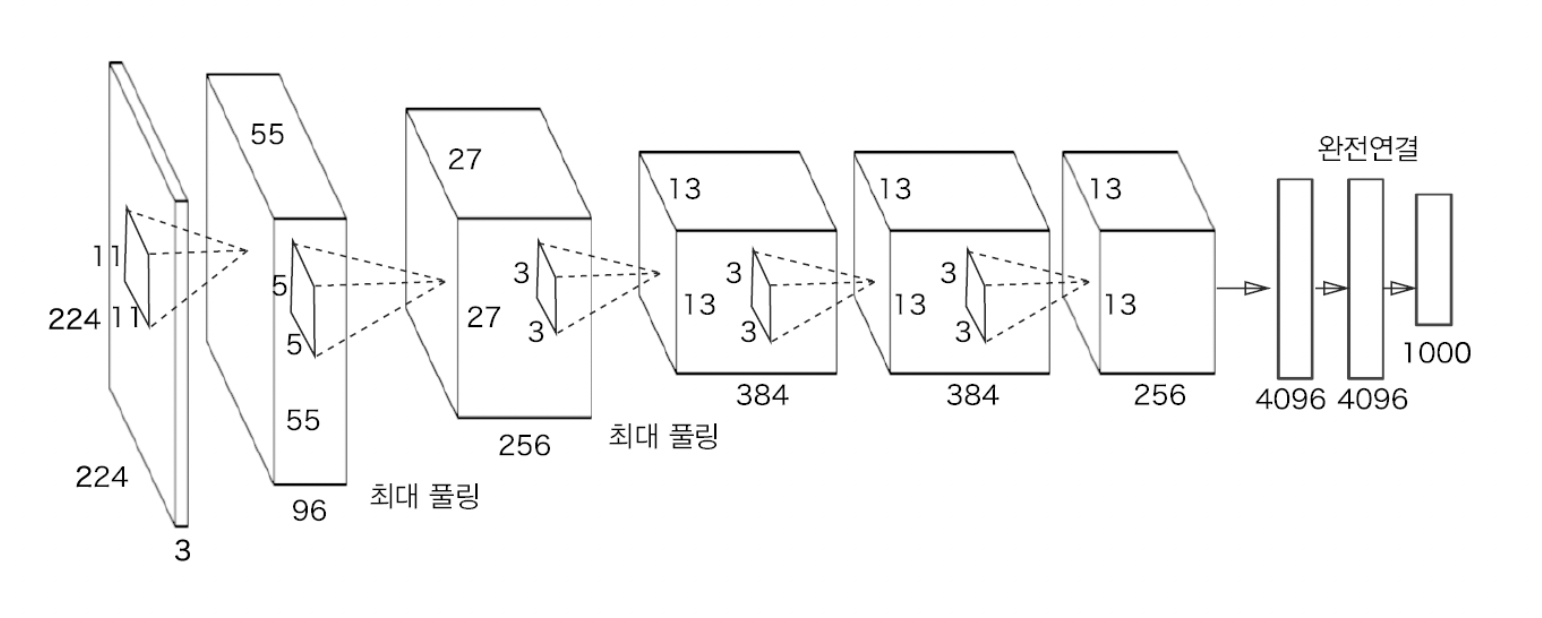기본적 구성은 LeNet과 크게 다르지 않다
합성곱 계층과 풀링 계층을 거듭하며 마지막으로 완전연결 계층을 거쳐 결과 출력
LeNet → AlexNet 변화
- 활성화 함수로 ReLU 이용
- LRN(Local Response Normalization)이라는 국소적 정규화를 실시하는 계층 이용
- LRN : Relu 함수를 사용할 때 Conv나 Pooling시 매우 높은 하나의 픽셀값이 주변의 픽셀에 영향을 미치게 되는 상황을 방지하기 위해 같은 위치에 있는 픽셀끼리 정규화
- 드롭아웃 사용
