[RL Course] Dynamic Programming 이해해보기

슥슥·2023년 4월 6일
강화학습
0

강화학습 기초 스터디

목록 보기
5/7

"파이썬과 케라스로 배우는 강화학습"이라는 도서로 공부를 하다가 개념이 헷갈려서 딥마인드의 David Silver 선생님께서 떠먹여주시는 강의를 조금씩 정리해보고자한다.
https://www.youtube.com/playlist?list=PLzuuYNsE1EZAXYR4FJ75jcJseBmo4KQ9-

여기서는 Markov Process, Markov Reward Process, Markov Decision Process에 대한 얘기는 생략할 것인데, 아마 나중에 CS234같은 강의를 보게 되면 그때 다시 한번 짚어보지 않을까 싶다.

1. Bellman Equation (MDP)

Value Function

State-Value function

state ss에서 시작했을 때, policy π\pi를 따를 경우 얻을 수 있는 reward의 기댓값

  • 시점 t로부터 얻을 수 있는 reward의 합 :  Gt\ G_t
  • 즉시 얻을 수 있는 reward :  Rt+1\ R_{t+1}
  • 다음 state에서의 value function의 할인된 값 :  γvπ(St+1)\ \gamma v_\pi(S_{t+1})
    vπ(s) = Eπ[ Gt ∣ St=s ] = Eπ[ Rt+1 + γvπ(St+1) ∣ St=s ]v_\pi(s)\ =\ E_\pi[\ G_t\ |\ S_t=s\ ]\ =\ E_\pi[\ R_{t+1}\ +\ \gamma v_\pi(S_{t+1})\ |\ S_t=s\ ]

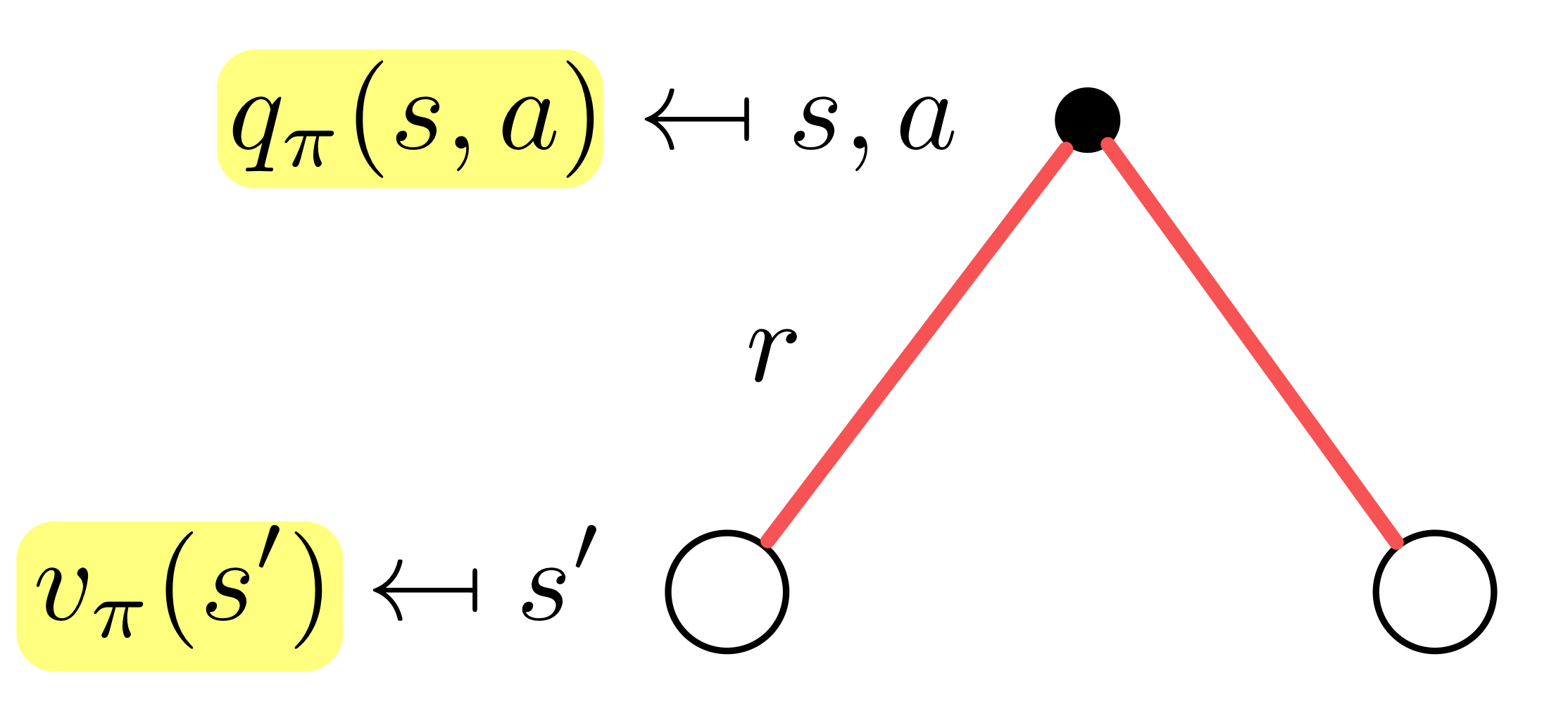
Action-Value function

state ss에서 시작했을 때, action aa를 선택하고, 이후 policy π\pi를 따를 경우 얻을 수 있는 reward의 기댓값

qπ(s,a) = Eπ[ Gt ∣ St=s, At=a ] = Eπ[ Rt+1 + γqπ(St+1,At+1) ∣ St=s,At=a ]q_\pi(s,a)\ =\ E_\pi[\ G_t\ |\ S_t=s,\ A_t=a\ ]\ =\ E_\pi[\ R_{t+1}\ +\ \gamma q_\pi(S_{t+1},A_{t+1})\ |\ S_t=s, A_t=a\ ]

해당 영상에서는 수식으로만 봤을때는 조금 헷갈릴 수 있는 부분을 그림으로 잘 표현해줘서 이해하는데 도움이 되었다.

Bellman Expectation Equation

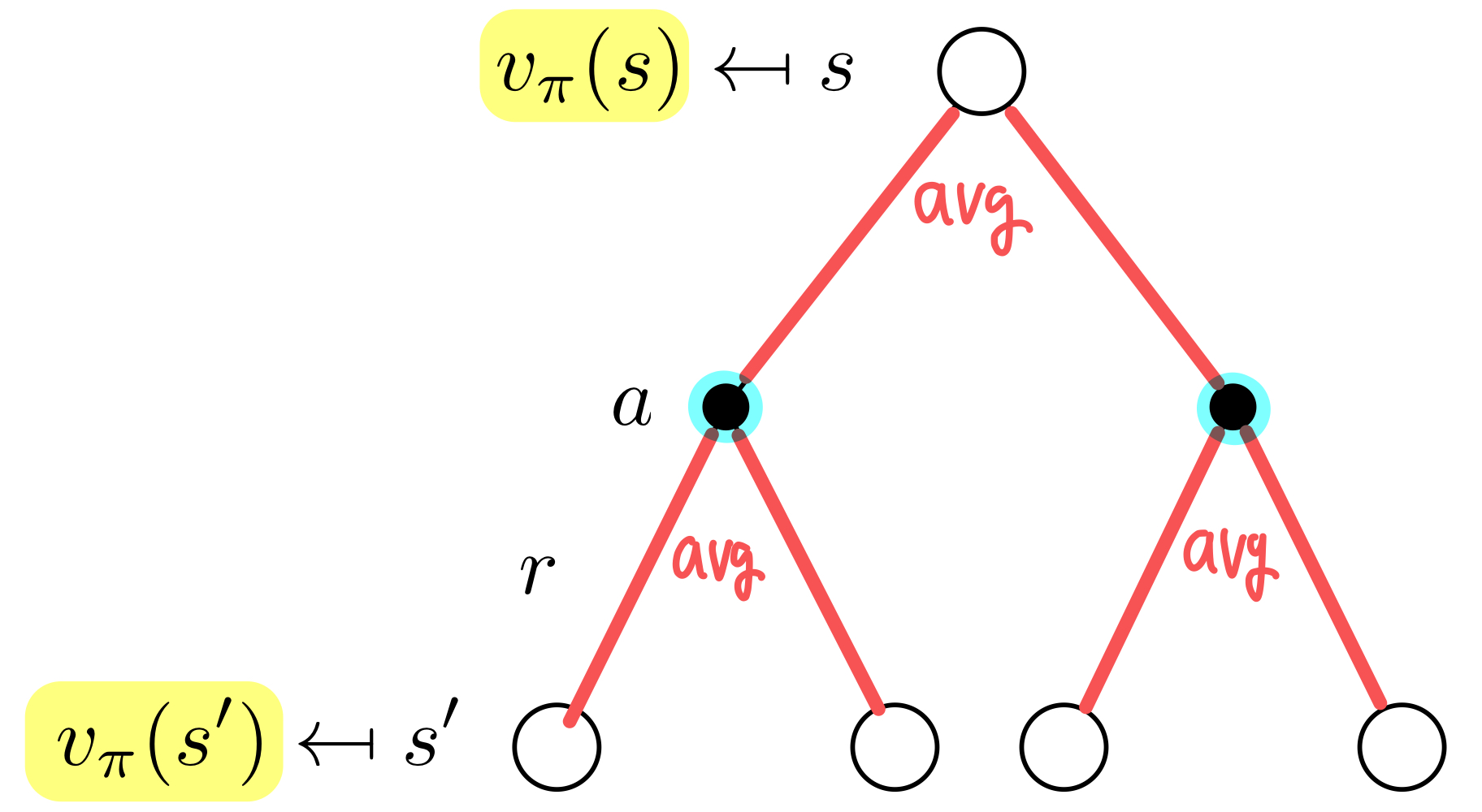
Bellman Expectation Equation for VπV^\pi

vπ(s) = ∑a∈Aπ(a∣s)qπ(s,a)v_\pi(s)\ =\ \sum_{a \in A}\pi(a|s)q_\pi(s,a)

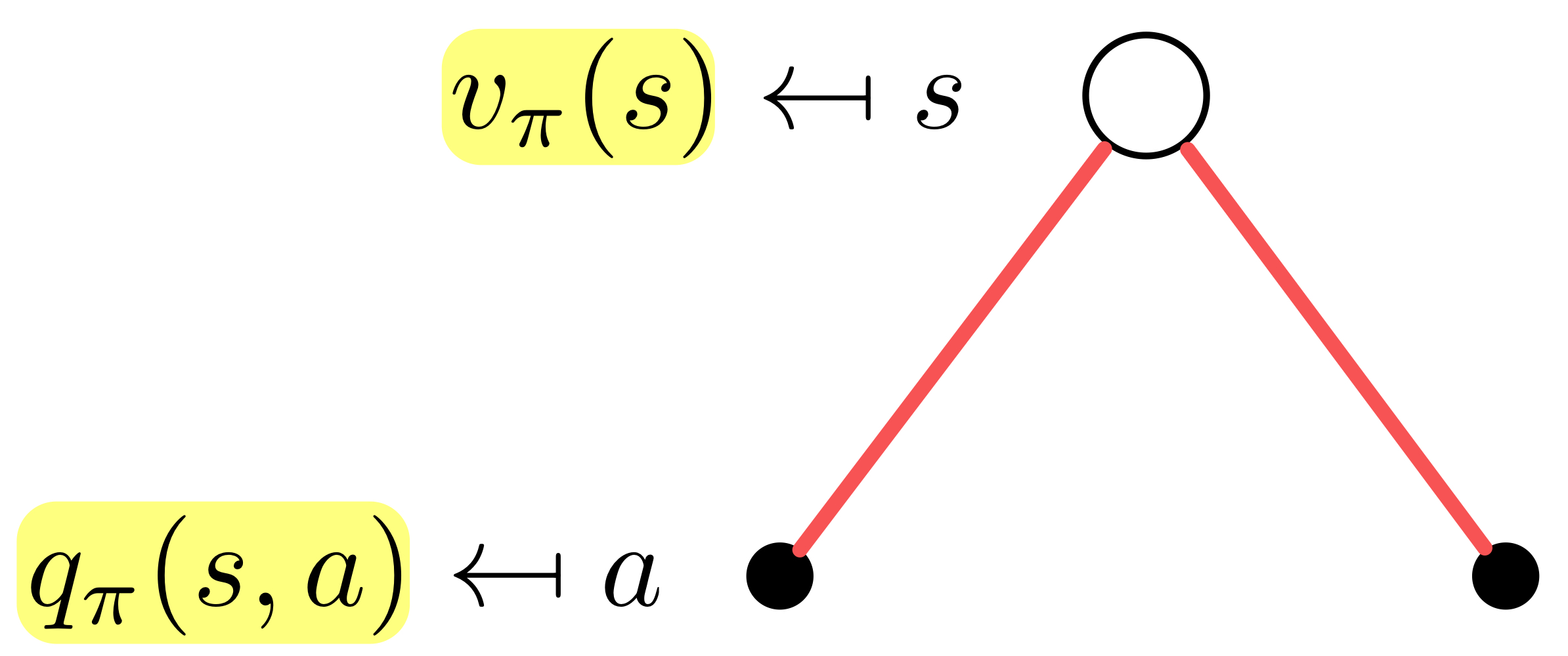
이 식을 해석해보면, 상태 ss, 정책 π\pi를 적용했을 때의 value function vπ(s)v_\pi(s)이
상태 ss에서 행동 aa를 선택할 확률 π(a∣s)\pi(a|s)에 상태 ss에서 행동 aa를 선택했을 때의 reward qπ(s,a)q_\pi(s,a)를 곱한 뒤 더한 평균값이라는 뜻이다!!

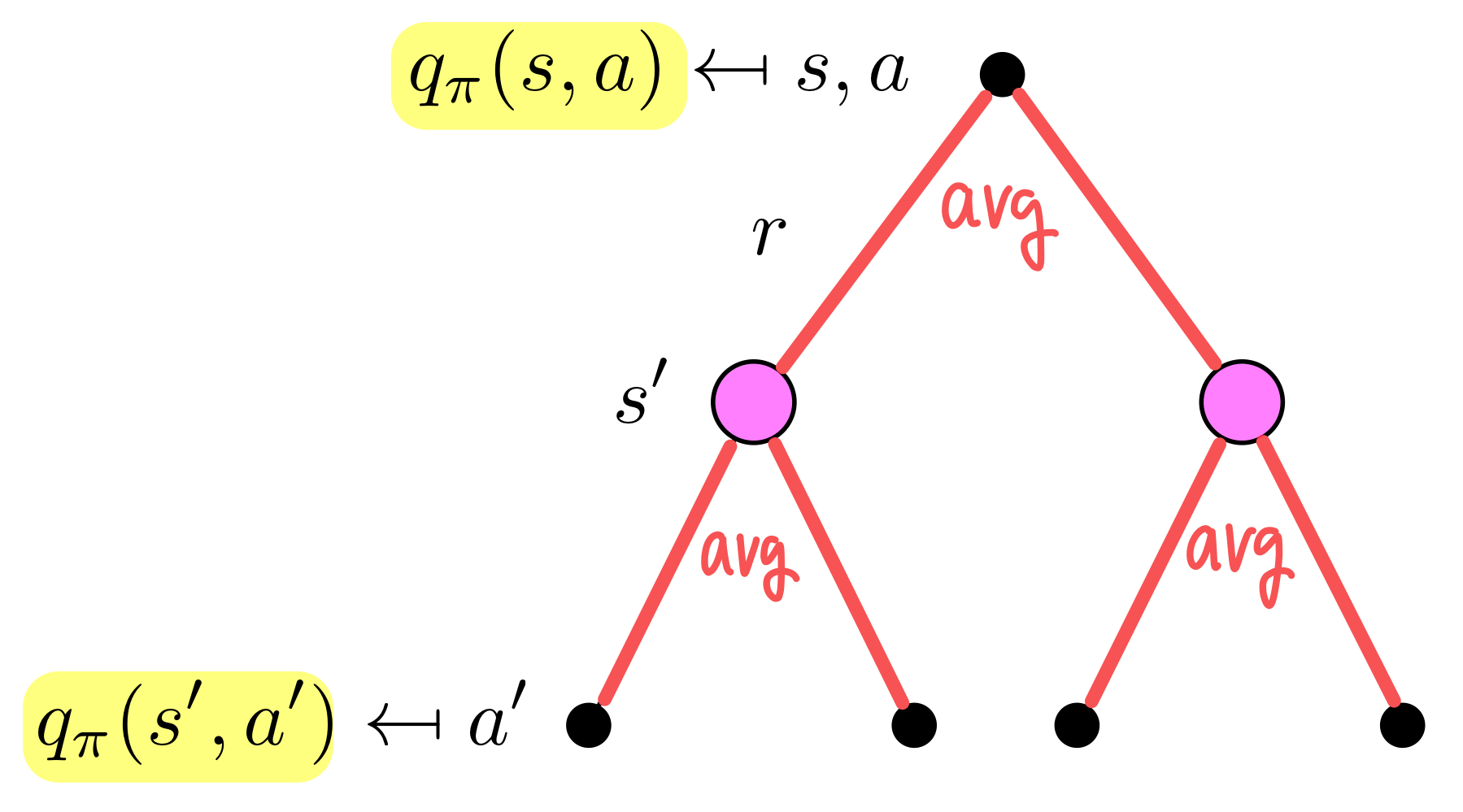
Bellman Expectation Equation for QπQ^\pi

qπ(s,a) = Rsa + γ∑s′∈SPss′avπ(s′)q_\pi(s,a)\ =\ R^a_s\ +\ \gamma \sum_{s' \in S} P^a_{ss'}v_\pi(s')

이 식을 해석해보면, 상태 ss에서 행동 aa를 선택했을 때 얻을 수 있는 reward qπ(s,a)q_\pi(s,a)가
행동 aa에 대한 reward RsaR^a_s에 행동 aa를 통해 상태 s′s'으로 갈 확률 Pss′aP^a_{ss'}과 다음 상태 s′s'에서 얻을 수 있는 value function vπ(s′)v_\pi(s')를 곱한 뒤 더한 평균값에 할인률 γ\gamma를 적용한 값을 더한 값이라는 뜻이다!!

Bellman Expectation Equation for vπv_\pi

위에서 본 식들을 조합하면 다음과 같은 식을 유도할 수 있다.

vπ(s) = ∑a∈Aπ(a∣s)(Rsa + γ∑s′∈SPss′avπ(s′))v_\pi(s)\ =\ \sum_{a\in A}\pi(a|s) \bigg(R^a_s\ +\ \gamma \sum_{s' \in S} P^a_{ss'}v_\pi(s')\bigg)

Bellman Expectation Equation for qπq_\pi

이 경우도 마찬가지로 위에서 계산한 식들을 조합해서 유도할 수 있다.

qπ(s,a) = Rsa + γ∑s′∈SPss′a∑a∈Aπ(a∣s)qπ(s,a)q_\pi(s,a)\ =\ R^a_s\ +\ \gamma \sum_{s' \in S} P^a_{ss'} \sum_{a \in A}\pi(a|s)q_\pi(s,a)


이렇게, 각 상태에서 value function을 계산하고 예측할 수 있는 방법을 알아냈다!! 그렇지만 아직 agent가 문제를 해결하기 위해서는 어떤 행동을 하는 것이 최적인지는 알 수 없다. 따라서 실제로 MDP를 해결하기 위해 optimal value function에 대해 알아보자.


Optimal Value Function

앞에서 봤던 value function은 polict π\pi가 주어졌을 때의 state, action value function을 구하는 방법이었다. 여기서는 최적의 행동 ∗*를 수행했을 때의 optimal한 value function을 계산한다.

Optimal State-Value function

v∗(s) = max⁡πvπ(s)v_*(s)\ =\ \max_\pi v_\pi(s)

굉장히 당연한 것이, optimal한 상태에서의 value function은 상태 ss에서 따를 수 있는 모든 policy 중에 가장 큰 value function을 값일 것이다. (maximum reward)

Optimal Action-Value function

q∗(s,a) = max⁡πqπ(s,a)q_*(s,a)\ =\ \max_\pi q_\pi(s,a)

Action Value function에서도 당연하게도 상태 ss에서 행동 aa를 선택했을 때, 가장 큰 reward가 최적의 값일 것이다. 한편, q∗(s,a)q_*(s,a)를 계산한다는 것은, 모든 상태 ss에 대해서 어떤 행동 aa에 대한 최고의 reward를 안다는 것이고, 이 말인 즉슨 최적의 policy ∗*를 구했다는 것이다. 다른 말로 하면 MDP를 해결한 것이다!!!

Optimal Policy

아래 식에서 보이다시피, q∗(s,a)q_*(s,a)를 최대로 만드는 행동 aa가 상태 ss에서 할 수 있는 행동 중 가장 큰 reward를 만들어내는 policy일 것이다.

π∗(a∣s)={1     if a=arg max⁡a∈Aq∗(s,a)0     otherwise\pi_*(a|s)= \begin{cases} 1 \ \ \ \ \ if \ a=\argmax_{a \in A} q_*(s,a) \\ 0 \ \ \ \ \ otherwise \end{cases}

Optimal Policy
Optimal Policy는 모든 state들에 대해서 다른 policy들보다 value function 값이 더 좋아야한다.

π≥π′     if   vπ(s)≥vπ′(s),  ∀s\pi \geq\pi' \ \ \ \ \ if \ \ \ v_\pi(s)\geq v_{\pi'}(s),\ \ \forall s

모든 MDP에 대해서,,,

  • 다른 모든 policy와 동일하거나 뛰어난 optimal policy π∗\pi_*가 반드시 존재한다!!!
  • 모든 optimal policy π∗\pi_*는 optimal value function v∗(s)v_*(s)을 도달한다!!!
    →  vπ∗(s) = v∗(s)\rightarrow \ \ v_{\pi_*}(s)\ =\ v_*(s)
  • 모든 optimal policy π∗\pi_*는 optimal action-value function q∗(s,a)q_*(s,a)을 도달한다!!!
    →  qπ∗(s,a) = q∗(s,a)\rightarrow \ \ q_{\pi_*}(s,a)\ =\ q_*(s,a)

Bellman Optimality Equation

Bellman Optimality Equation for v∗v_*

v∗(s) = max⁡aq∗(s,a)v_*(s)\ =\ \max_aq_*(s,a)

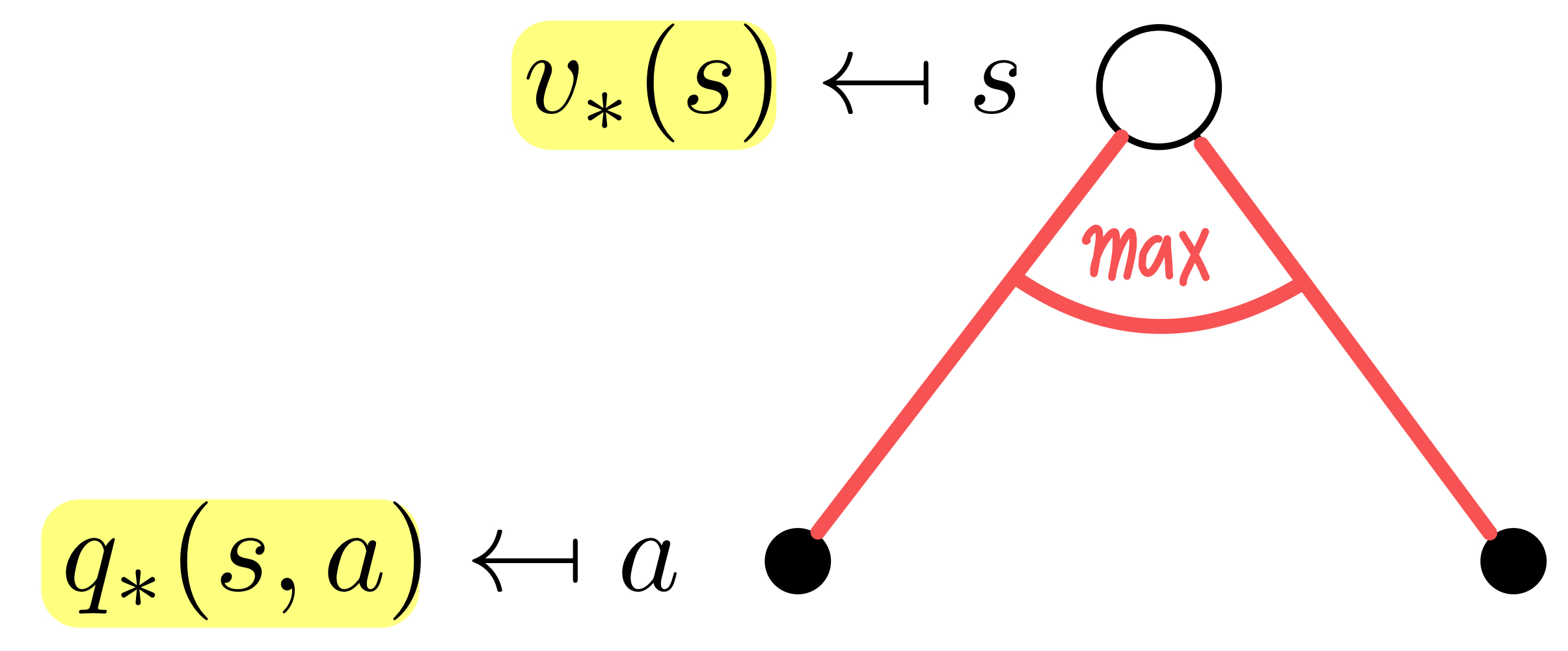
아까 Bellman Expectation고 달라진 것을 확인할 수 있다.
Bellman Expectation에서는 확률값과 value function을 곱해서 합하는 평균을 구하는 것이 목표였다면, Bellman Optimality에서는 상태 ss에서 각 행동에 대한 reward q∗(s,a)q_*(s,a)를 maximize하는 행동 aa를 했을 때의 value function v∗(s)v_*(s)를 구하는 것이 목표이다!!!

Bellman Optimality Equation for Q∗Q^*

q∗(s,a) = Rsa + γ∑s′∈SPss′av∗(s′)q_*(s,a)\ =\ R^a_s\ +\ \gamma \sum_{s'\in S}P^a_{ss'}v_*(s')

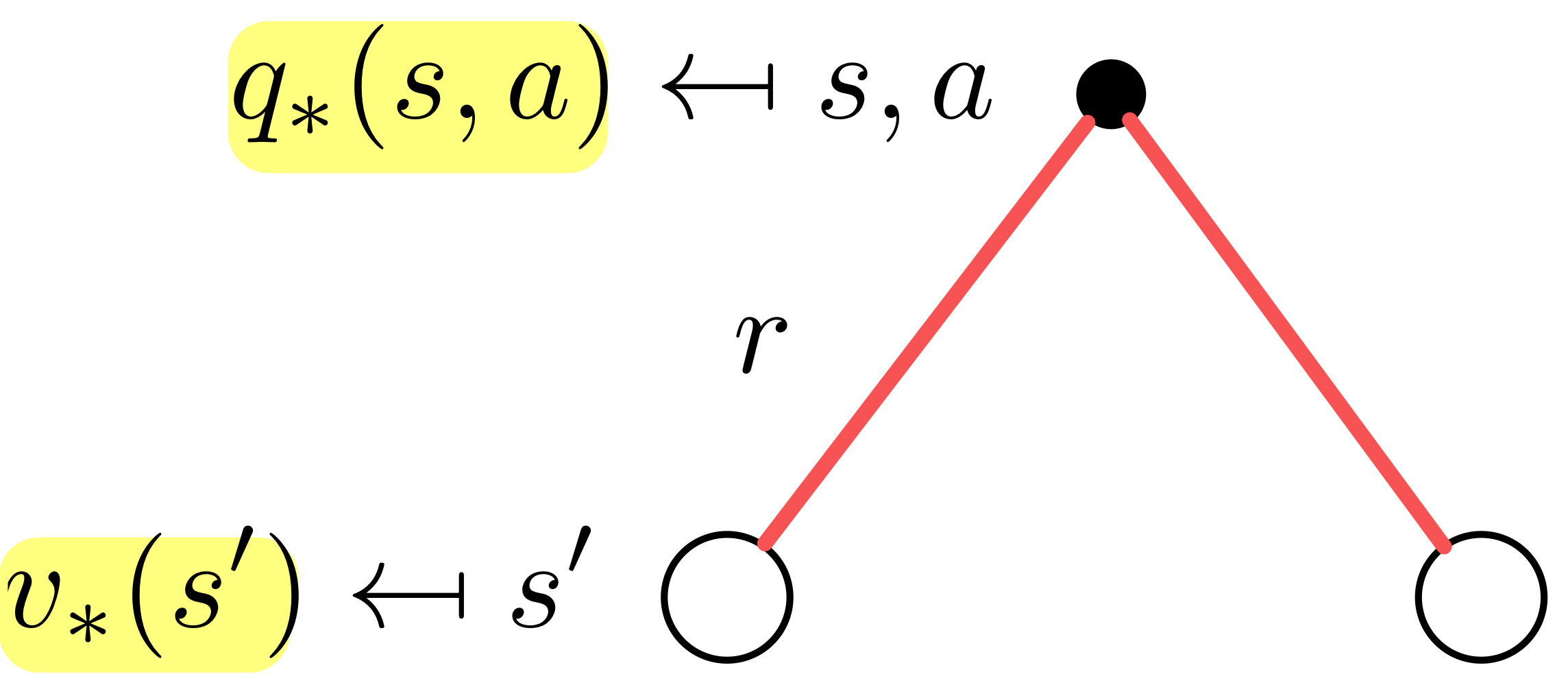
이 식이 무슨 뜻인지 뜯어보면, q∗(s,a)q_*(s,a)는 행동 aa로 얻을 수 있는 보상 RsaR^a_s에 상태 ss에서 행동 aa를 했을 때 갈 수 있는 다음 상태 s′s'에서의 최대 reward v∗(s′)v_*(s')에 확률 Pss′aP^a_{ss'}을 곱한 뒤 더한 평균값에 할인율은 적용한 값을 더한 값이라는 뜻이다!!!

Bellman Optimality Equation for V∗V^*

v∗(s) = max⁡aRsa + γ∑s′∈SPss′av∗(s′)v_*(s)\ =\ \max_a R^a_s\ +\ \gamma \sum_{s'\in S}P^a_{ss'}v_*(s')

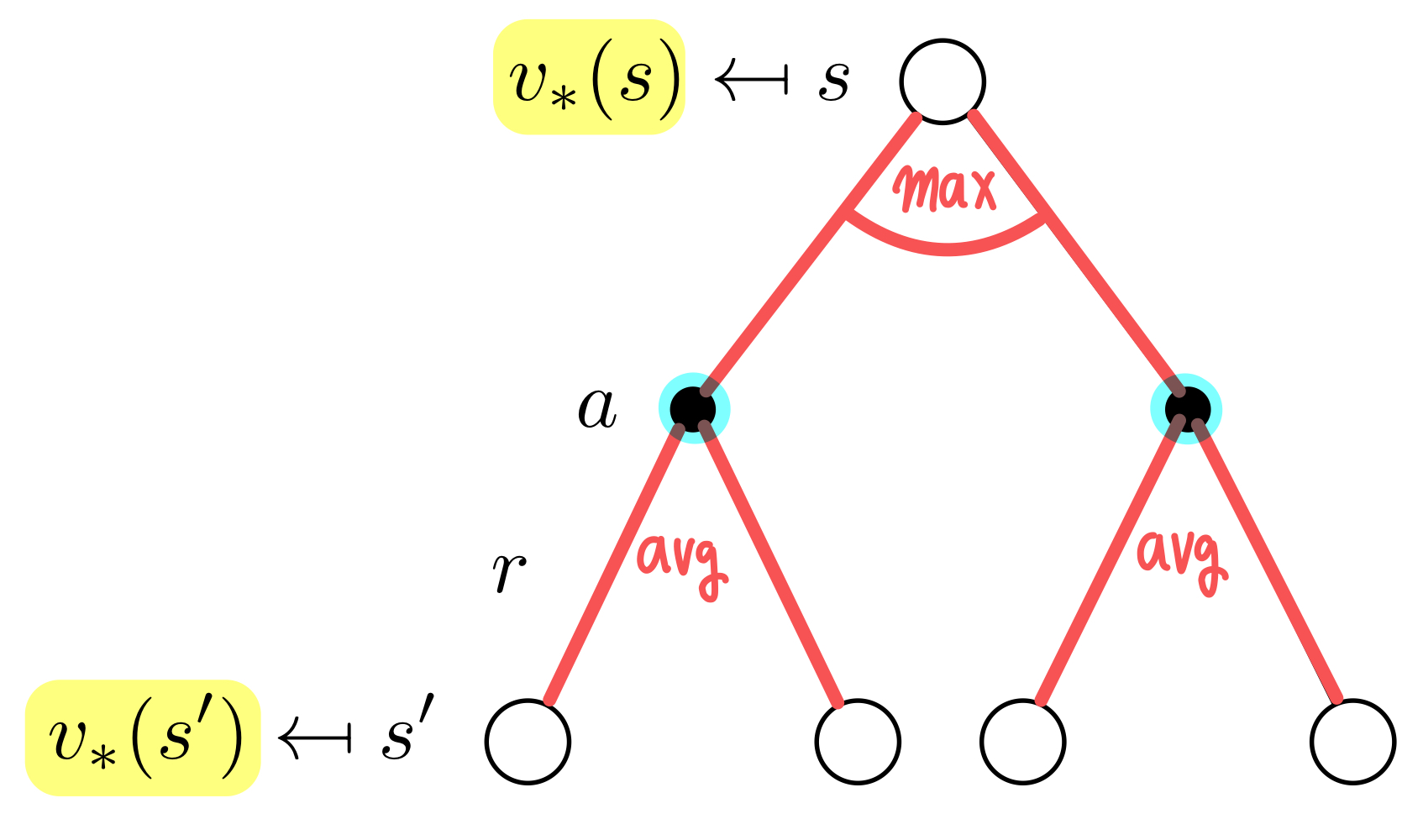
Bellman Optimality Equation for Q∗Q^*

q∗(s,a) = Rsa + γ∑s′∈SPss′amax⁡aq∗(s,a)q_*(s,a)\ =\ R^a_s\ +\ \gamma \sum_{s'\in S}P^a_{ss'}\max_aq_*(s,a)


우리 목표는 Bellman Optimality Equation을 푸는 것이지만, closed form으로 문제를 정의할 수도 없고, 비선형 문제인 경우가 많다. 따라서 일반적으로는 iterative한 형태로 문제를 해결한다. 이번 게시물에서는 그 대표적인 방법인 Policy Iteration와 Value Iteration을 다룬다.


2. Dynamic Programming

Dynamic Programming에서 Dynamic 하다는 것은 연속적이거나 일시적인 부분들로 이루어졌다는 의미이고, Programming이라는 것은 어떤 문제에 대한 최적화를 한다는 것이다.

어떤 복잡한 문제를 해결하기 위해 작은 문제로 나누어서 해결해나가는 방법으로, 두가지 속성을 지닌다.

  • Optimal Structure
    • 큰 문제들의 optimal solution은 작은 문제들의 optimal한 solution으로 해결 가능
    • Divide & Conquer과 비슷한 의미를 가짐
  • Overlapping Subproblems
    • Divide & Conquer과 다른 점은, 작은 문제들이 반복해서 발생한다는 점
    • 작은 문제들의 solution이 저장되고 다른 작은 문제에 동일하게 적용 가능

앞서서 유도했던 MDP의 Bellman Equation들을 살펴보면 이러한 속성을 지니고 있음을 알 수 있다.

  • Bellman Equation은 재귀적인 형태로 구성되어있으므로 큰 문제를 작은 문제로 분할해서 해결 가능하고,
  • 각 value function은 해당 상태 ss 에서의 값을 저장하기 때문에 다른 문제를 해결할 때에도 동일하게 사용이 가능하다.

앞으로 Prediction과 Control이라는 용어가 나올 것인데, 한번 짚고 넘어가자!!

  • Predict
    • MDP의 정보<S,A,P,R,γ><S, A, P, R, \gamma>와 특정 Policy π\pi가 주어졌을 때, 해당 policy에 대한 Value Function vπv_\pi를 구하는 것!!!
    • 해당 Policy를 평가할때 사용됨
  • Control
    • MDP의 정보<S,A,P,R,γ><S, A, P, R, \gamma>가 주어졌을 때, Optimal Policy π∗\pi_*를 구하는 것!!!
    • 해당 Policy를 개선하거나, 최적의 Policy를 찾을 때 사용됨

3. Policy Iteration

Policy Evaluation

매 Iteration마다 Bellman Expectation을 사용해서 주어진 Policy π\pi를 평가하는 Predict 과정이다. 즉, 주어진 Policy에 대한 Value Function을 계산한다.

매 iteration마다 모든 state에 대한 value function을 update한다.

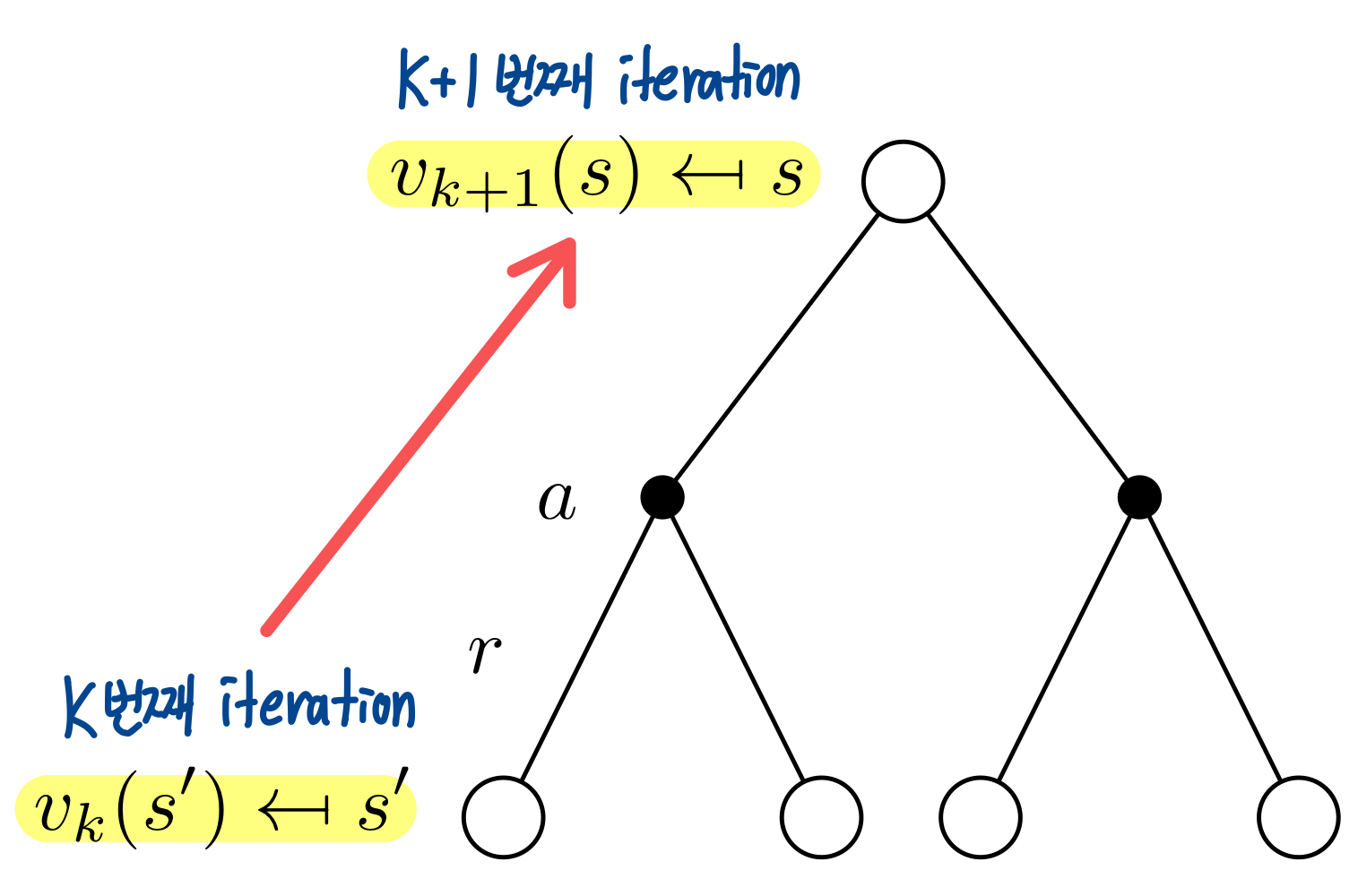
vk+1 = ∑a∈Aπ(a∣s)(Rsa + γ∑s′∈SPss′avk(s′))v_{k+1}\ =\ \sum_{a\in A}\pi(a|s)\Big(R^a_s\ +\ \gamma \sum_{s'\in S }P^a_{ss'}v_k(s')\Big)

초기에 어떤 Policy π\pi를 고정시킨 뒤, State-Value Function을 계속해서 update해 나가는 것이다.
Iteration을 무한히 반복했을 때, 해당 Value Function에 대한 Policy는 Optimal하다!

Grid World 예제에서 한번 살펴보자.

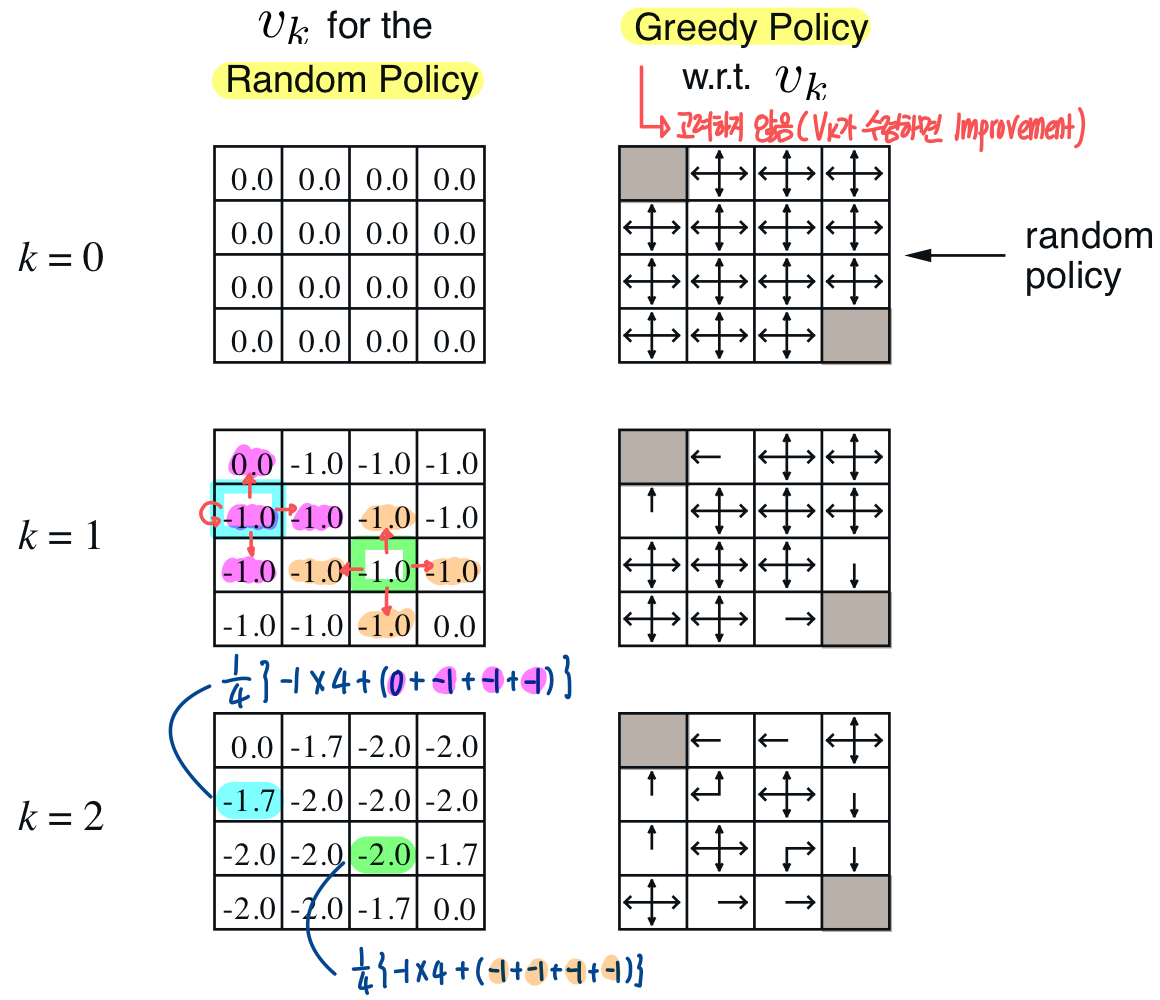
Bellman Expectation Equation을 사용하기 때문에 iteration을 진행함에 따라 현재 policy를 따랐을 때의 각 state에 대한 value function이 update되는 것을 볼 수 있다.

이 경우 random한 초기 policy를 고정시킨 상태에서 value function을 update시키는 것이다. 오른쪽에 있는 policy는 각 value function를 고려했을 때 policy를 나타낸 것인데, 방금 말했듯이 policy는 고정시킨 상태에서 iteration을 진행한다.

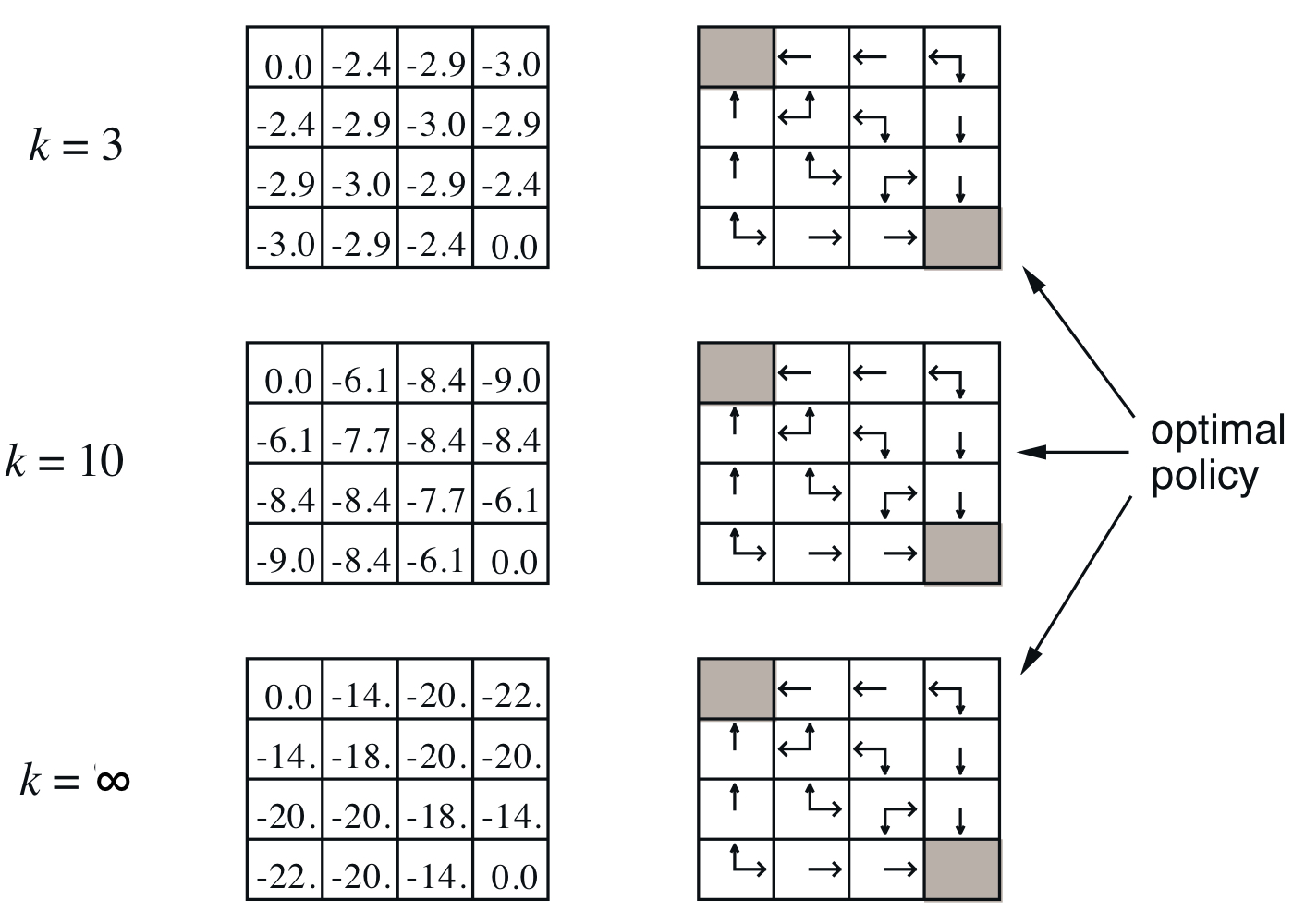
k=3이후부터는 value function 값은 변하지만 policy는 그대로인 것을 볼 수 있다. 한 iteration이 끝나면 뒤에서 볼 Policy Imporvement를 진행한다.

위에서 보이는 작은 GridWorld에서는 Policy Evaluation을 통해 산출된 Policy가 최적의 Policy였다. 그러나, 일반적인 상황에서는 산출된 Policy에 대한 Imporvement와 Evaluation이 반복되어야 최적의 policy π∗\pi_*로 수렴할 수 있다.

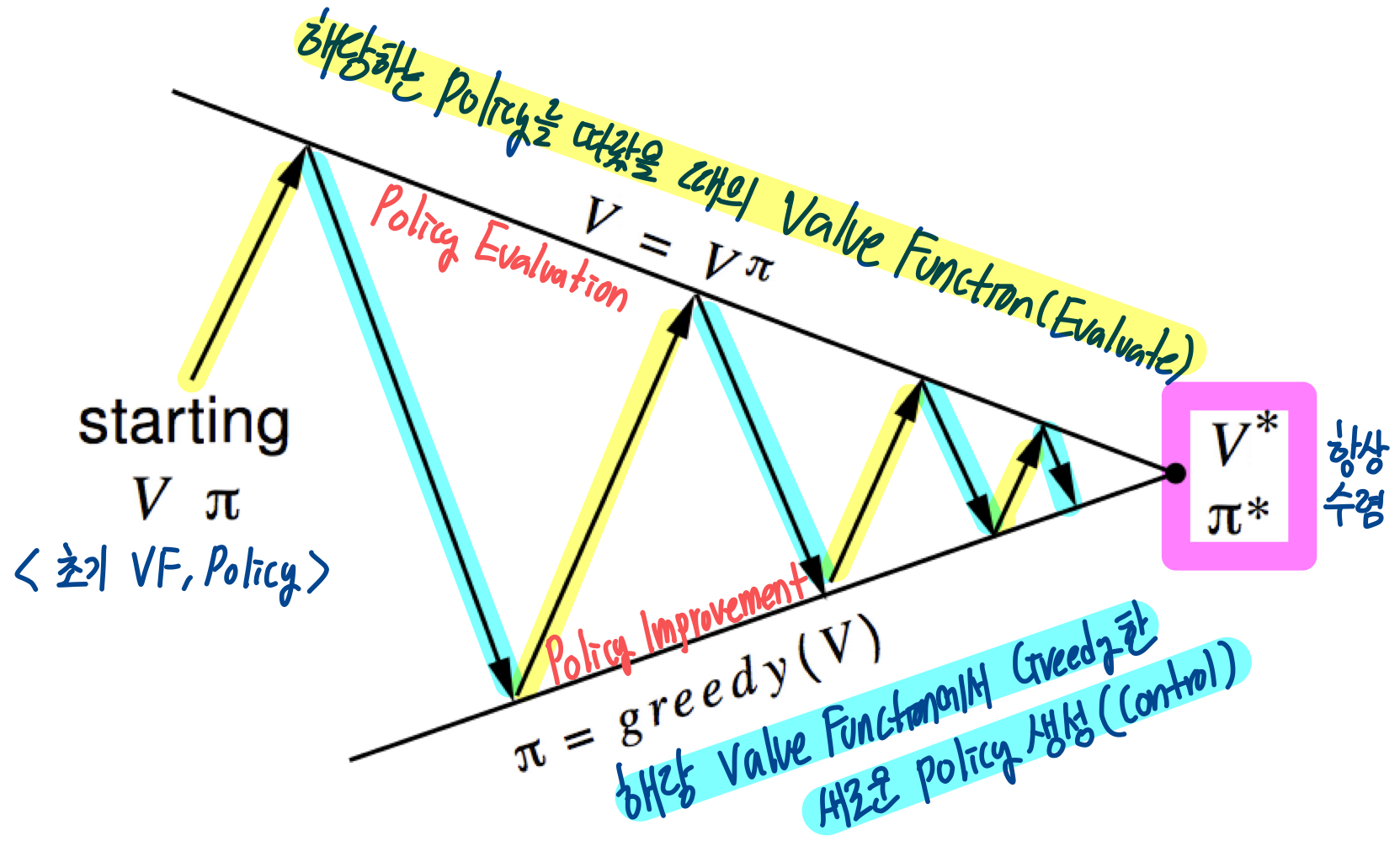
Policy Evaluation : 주어진 policy에 대해서 vπv_\pi 계산
Policy Improvement : 계산된 vπv_\pi에 대해 greedy한 방식으로 개선된 policy π′\pi' 산출


Policy Improvement

Policy Evaluation으로 현재 Policy가 어떤 Value Function을 가지는지 찾아냈다면, 그 Value Function에 대해서 가장 큰 Reward를 만들어낼 수 있는 개선된 Policy를 만들어야한다.

이 과정을 식으로 표현하면,
현재의 policy : a =π(s)a\ = \pi(s)
Evaluation 이후 greedy 개선된 Policy : π′(s) = arg max⁡a∈Aqπ(s,a)\pi'(s)\ =\ \argmax_{a \in A} q_{\pi}(s,a)

지금 당장 greedy하게 선택한 policy는 적어도 기존의 policy보다 동일하거나 뛰어나기 때문에, iteration을 반복하면 최적의 Policy에 도달할 수 있다!!

Value Function이 더이상 개선되지 않는 상태(qπ(s,π′(s) = max⁡a∈Aqπ(s,a)q_\pi(s,\pi'(s)\ =\ \max_{a \in A} q_\pi(s,a)) 에 도달하면 Bellman Optimality Equation을 만족한다. 모든 state ss에 대해 vπ(s) = v∗(s)v_\pi(s)\ =\ v_*(s) 이고, 그때의 policy가 최적의 policy π∗\pi_*)이다.


잘 보면, value function이 수렴할때까지 Policy Evaluation을 반복해야한다. 근데 꼭 참 value function vπv_\pi이 수렴해야만 할까?? 위에서 본 예시만 봐도 k=3 이후부터 policy가 변하지 않는데 굳이???
→\rightarrow 변화량이 작거나, 몇번의 Evaluation을 진행하면 바로 Improvement를 하고 싶은데!!
→\rightarrow 더 나아가서, 그냥 value function을 한번 구할때마다 개선하면 안될까??

이렇게 나온게 Value Iteration 아이디어


4. Value Iteration

굉장히 당연하지만, Optimal한 Policy는 크게 두 개의 요소로 쪼갤 수 있다.
초기 상태에서의 최적의 action A∗A_* + 이후 상태S′S'
에 대한 최적의 Policy

즉, 상태 ss에 대해서 다음과 같은 조건을 만족하면 policy π(a∣s)\pi(a|s)가 optimal value를 도달한다.
1) ss에서 도달할 수 있는 상태 s′s'에 대해서
2) π\pi가 s′s'에서의 최적의 value function을 도달할 때

그럼 state s′s'에서의 v∗(s′)v_*(s')를 도달하는 최적의 solution을 알고 있다면, ss에서 어떤 행동을 해야할지도 알게 된다는 뜻이다. 직관적으로 생각해보면, 마지막 reward에서 한 step씩 거꾸로 되돌아오면 최적의 policy를 구할 수 있다고 이해할 수 있다.

이 경우에 현재 value function이 어떤 policy에서 나온 것인지는 중요하지 않다. 그냥 Bellman Optimality Equation에 따라서 각 state별로 max reward를 가질 수 있도록 value function만 업데이트 시킨다.

vk+1(s) = max⁡a∈A(Rsa + γ∑s′∈SPss′avk(s′))v_{k+1}(s)\ =\ \max_{a\in A} \bigg(R^a_s\ +\ \gamma \sum_{s' \in S} P^a_{ss'}v_k(s')\bigg)

Policy Iteration에서처럼 Grid World 예제를 보자

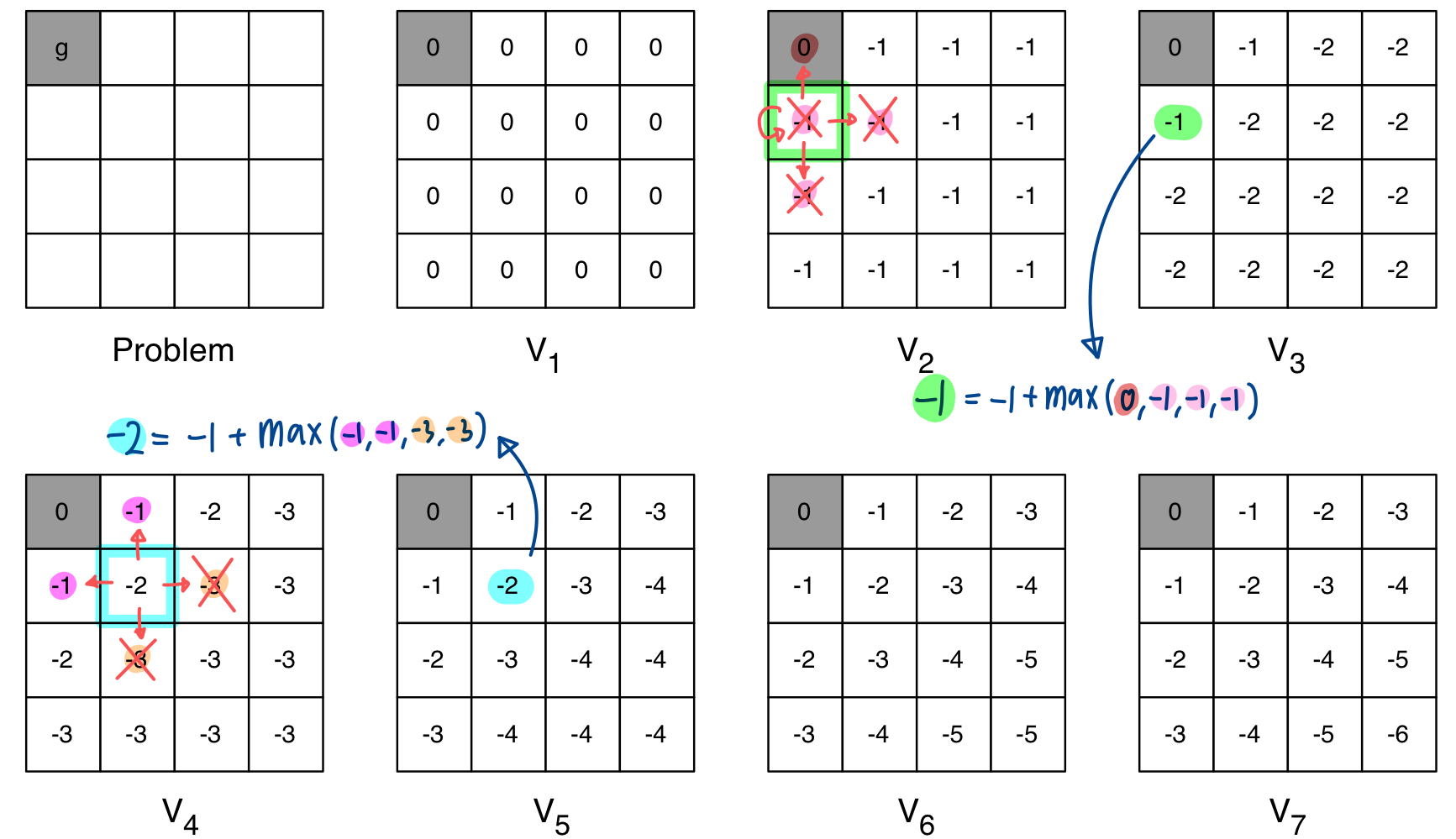
위에서 봤던 Policy Iteration과 다르게 value function에 대한 policy는 전혀 중요한 고려사항이 아니다. 그리고, Policy Evaluation에서는 Bellman Expectation으로 평균을 구했었다면 Value Iteration에서는 Bellman Optimality로 value function의 최대값만을 고려해서 update를 진행한다.


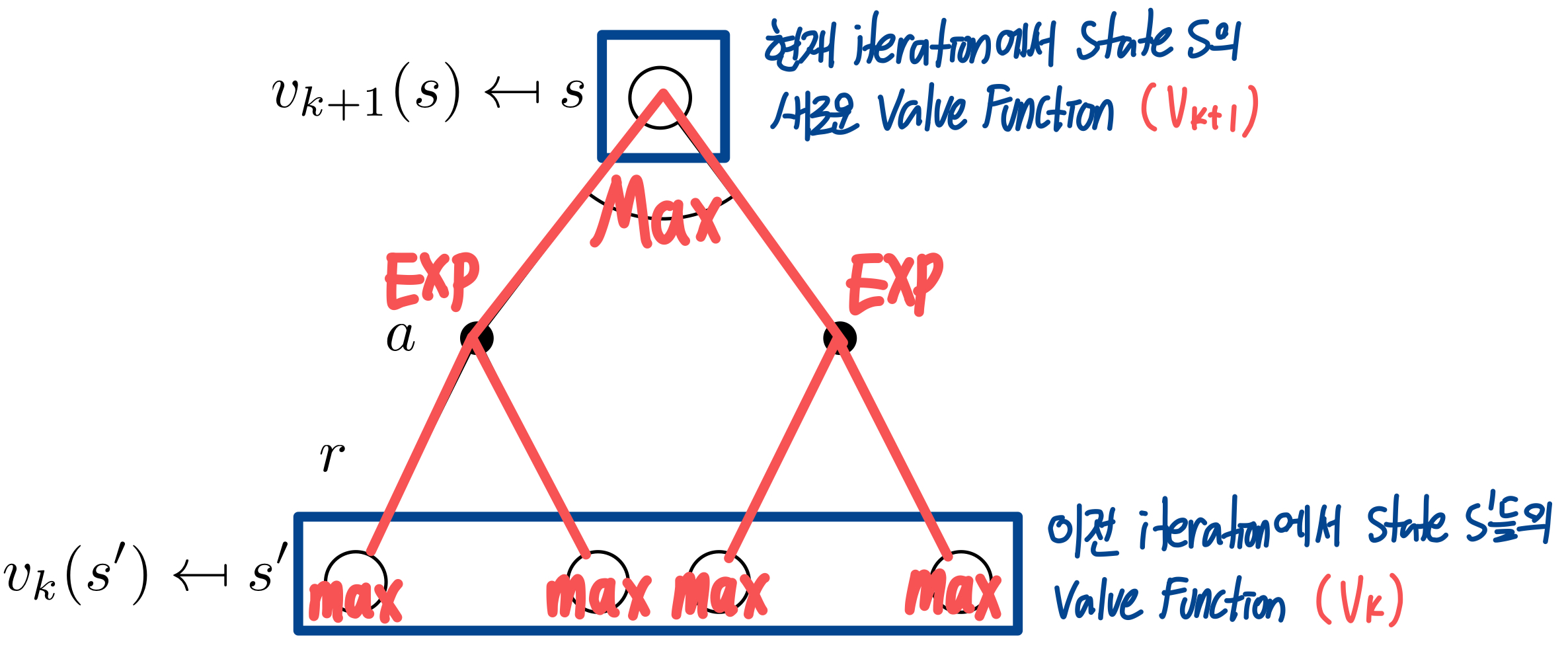
5. Summary

지금까지 본 Synchronous DP 알고리즘을 요약하면 다음과 같다.

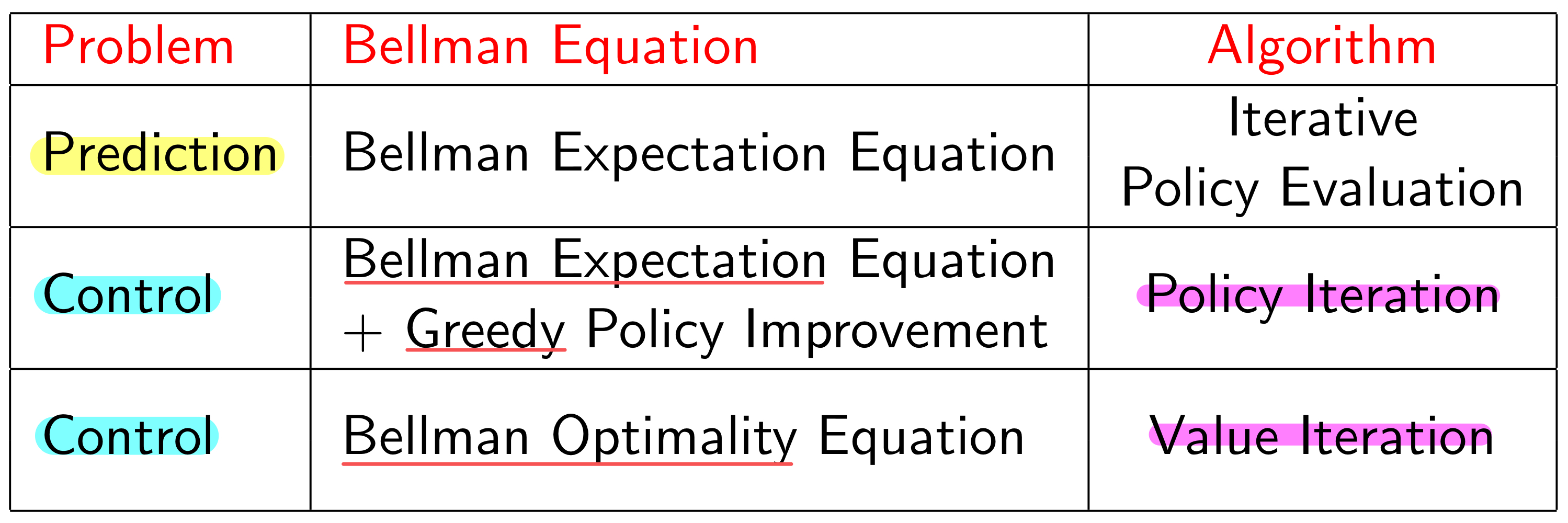
이런식으로 이해를 하면 되고, 차이가 뭔지 모르겠으면 위에 grid world 예제에서 원리를 이해하면 편할 것 같다.


6. Asynchronous DP

Summary에서 Synchronous DP라는 표현을 사용했는데, 이는 한번에 모든 state를 고려하여 update가 진행되는 방식을 말한다. 이와 반대로, Asynchronous DP는 각 state를 개별적으로 고려하여 따로 update를 시키는 방식이다. 이런 방식을 사용하는 핵심 아이디어 몇개를 살펴보자.

In-Place Dynamic Programming

Synchronous DP 같은 경우에는 한 state에 대해 value function을 update를 시켰더라도, 다른 state들에 대해 update할 대에 leaf node 형태로 사용될 수 있기 때문에, 이전 step에서의 정보를 저장해놔야한다.

그렇지만, Asynchronous DP는 개별적으로 update를 하기 때문에 굳이 이전 step에서의 정보를 저장해둘 필요없이, update된 값을 그대로 사용하면 된다!!

Prioritised Sweeping

Prioritised Sweeping 같은 경우에는 udpate를 진행할 때에, 어떤 state에 대한 value function을 먼저 update할 지에 대한 결정이다. 이전에는 모든 state를 한번에 update하기 때문에 이를 고려하지 못했지만, Asynchronous DP에서는 주변 state들에 많은 영향을 끼치는 state부터 update 시킬 수 있을 것이다.

이 경우, 한 iteration에서 가장 많이 update되는 state 순서대로 priority queue를 만들어서 그 순서대로 업데이트를 진행할 수 있다. Update되는 정보를 Bellman Error라고 하고, 다음식으로 표현한다.

∣max⁡a∈A(Rsa + γ∑s′∈SPss′a) − v(s)∣\left\lvert \max_{a\in A} \Big(R^a_s\ +\ \gamma \sum_{s'\in S} P^a_{ss'}\Big)\ -\ v(s) \right\rvert

Real-Time Dynamic Programming

한번에 모든 state를 고려하지 않고, 개별적으로 update를 진행한다는 것은 에이전트의 입장에서는 자신이 실제로 방문하고 있는, 혹은 관련이 있는 state들에 대해서 선별적으로 update를 할 수 있다는 것이다.



이렇게 David Silver 선생님 강의로 헷갈렸던 부분을 보충했다. 지금까지 올렸던 게시물 기준으로는 2번째 게시물까지의 내용을 다뤘는데, 당분간은 책 내용 대신 영상 내용을 요약 정리하게 될 것 같다.

profile
슥슥
이전 포스트

[강화학습 이론] 4장_강화학습 기초3 : 그리드월드와 큐러닝 2

다음 포스트

[RL Course] Monte Carlo, Temporal Difference로 Model Free Prediction 하기

0개의 댓글